一种表示流形形体和非流形形体的统一数据结构研究

张成林，朱 琳，文珊珊，王 卓，王联凤

(1.中国科学技术大学 工程科学学院,安徽 合肥 230026； 2.上海交通大学 机械与动力工程学院,上海 200240；3.上海航天设备制造总厂,上海 200245)

一种表示流形形体和非流形形体的统一数据结构研究

张成林1，朱 琳2，文珊珊3，王 卓3，王联凤3

(1.中国科学技术大学 工程科学学院,安徽 合肥 230026； 2.上海交通大学 机械与动力工程学院,上海 200240；3.上海航天设备制造总厂,上海 200245)

为弥补3D打印中非流形拓扑数据结构的存储空间大、运算效率低，流行拓扑数据结构形体表示的局限性，研究了一种可表示流形形体(正则形体)和非流形形体(非正则形体)的统一数据结构。分析了半边数据结构、放射边数据结构、混合边数据结构、单元复形和粘合边数据结构等非流形形体的边界表示法，发现现有的数据结构未能综合考虑几何模型、存储数据和效率。提出了一种基于复形的非流形数据结构：利用引用面、边及点结构完整地表示非流形几何模型，实现线框、表面、实体和自由曲面模型的统一；采用面向对象的设计方法，使用类的继承与派生，以减少数据存储量，提高存储和运算效率；扩展欧拉算子可为更高级的欧拉操作和布尔操作提供基础。设计的方法在模型的面、边和点的数据设计中，以指针的形式管理和组织拓扑结构，避免信息的重复存储，既满足了丰富的形体表示需求，扩大了传统3D打印模型的覆盖域，又有效减少了存储空间，提高了运算效率。

3D打印； 几何模型； 流形形体； 非流形形体； 数据结构； 拓扑结构； 运算效率； 存储空间

0 引言

工程应用对3D打印的几何模型提出高要求，而拓扑数据结构作为关键部分，其运算效率及存储空间优化严重制约3D打印模型处理的功能和效率。目前，几何模型主要有流形拓扑数据结构和非流形拓扑数据结构两种表示方法。非流形拓扑数据结构可表示更丰富的形体，代价是存储空间的增长和运算效率的降低；流形拓扑数据结构存储空间相对较小，运算效率相对较高，但其形体表示有一定的局限性。非流形模型的提出，虽然是源于几何模型理论的需要，但更主要的是3D打印技术对模型显示提出更高要求，必然会混合使用线框、曲面、实体模型，非流形模型能很好地满足其要求[1]。以表面拓扑的观点，非流形形体是一个由0，1，2，3维几何元素组成的混合维形体，可有悬边、悬面和孤点。以点集的观点，非流形形体可能具有内部边界或不封闭的边界，也可以是开的点集。目前已出现了4种形体表示方法：基于s集的表示方法、边界表示方法(B-rep)、SGC表示方法和CNRG表示方法。其中：以边界表示方法为主流的实体造型技术支撑了一代CAD/CAM系统，并在各应用领域发挥了巨大作用[2-3]。但目前现有的数据结构均未有效结合完整表示非流形几何模型及减少存储数据、提高运算效率，因此研究一种满足上述目标的非流形数据结构十分迫切。为此，本文对一种表示流形形体和非流形形体的统一数据结构进行了研究。

1 边界表示法

边界表示方法能提供形体完整的边界信息，以翼边数据结构为代表的边界表示方法在传统实体造型技术中有重要的地位。对非流形形体的边界表示，大量研究是在翼边数据结构基础上进行扩充和完善[4]。

1.1半边数据结构

半边数据结构是MANTYLA基于翼边数据结构创建的[2]。半边数据结构将翼边数据结构中的一条整边拆成两条半边，每条半边各带1个顶点作为起点，通过体(solid)-面(face)-环(loop)-半边(halfedge)-顶点(vertex)五层拓扑描述形体。此外，为表示面与面间的相互联系，又引入了一个边(edge)附加拓扑元素联系一对半边，通过边对邻接面进行描述。这样，半边、边和顶点三个拓扑元素就构成了半边数据结构的最核心部分。半边数据结构对表面流形表示进行了扩展，将非流形按特殊情况或伪流形进行处理，使非流形表示变得自然。但半边数据结构的提出并非是为建立一种表示非流形形体的数据结构，其表示的形体是具非流形边界的正则形体。

1.2放射边数据结构

文献[5]对非流形形体的表示进行了开创性研究，其研究目标是用统一的数据结构表示线框、表面和实体模型，允许在产品模型中存储任何几何信息。针对非流形形体中一条边可有多个邻面的情况，提出了放射边数据结构的构想：在放射边数据结构中，使用的几何信息是面、环、边、顶点，其拓扑层次是由模型(model)、区域(region)、壳(shell)、面引用(faceuse)、环引用(loopuse)、边引用(edgeuse)、点引用(vertexuse)组成。放射边数据结构将面、环、边、点的几何定义与其引用分离，使模型中的不同拓扑元素可共享相同的几何信息，从而保证非流形形体数据的一致性。放射边数据结构是第一种面向非流形形体表示而提出的数据结构，全面考虑了一般非流形形体的情况，实现了用统一的数据结构表示非流形形体的目标，提供了较正则形体更强的形体定义功能，为实现更简单而统一的算法奠定了基础。

1.3混合边数据结构

文献[6]提出的混合边数据结构的基本思想是利用拓扑元素的层次性，将一个复杂几何形状表示为多个简单几何元素的组合。在混合边数据结构中，每条边的表示通过3个记录实现：线段(segment)记录2个和边记录1个，其算子被分为低层、中层、高层3个层次，高层算子根据低层算子构造，使其不涉及特定的实现细节，低层算子完成特定的工作。从概念上来说，混合边数据结构是翼边数据结构和半边数据结构的组合，它在线段的层次维护多边形(面)和实体的方向信息，在边的层次处理面的邻接信息，线框、表面和实体的混合表示在形状(shape)的层次统一。算子的层次性构造避免了操作的冗余并增强了模型的语义集成。混合边数据结构实现了线框、表面、实体三种模型的统一与集成，但其表示的实体限于正则形体。

上述的边界表示方法均建立在直观的概念基础上，但一个完整的非流形形体的数学定义对无二义地描述非流形形体至关重要。传统的边界表示是以流形作为其数学基础，作为流形概念的自然扩展，非流形形体的边界表示是以复形(complex)作为其数学基础。

1.4单元复形

文献[7]将非流形形体定义为数学上满足三个条件的n维单元复形(n-cell complex)的集合。其中：第一个条件是三维单元复形能用0，1，2，3维单元的集合表示，即非流形模型可包含分离的顶点、边、面和体；第二个条件是每个单元边界必须由低维单元构成，因而非流形模型总是封闭的；第三个条件是要求所有拓扑元素不能出现自相交。此模型被称为基于复形的非流形几何模型，其拓扑层次结构如图1所示。根据有限单元复形的Euler-Poincare公式，理论上只需9个独立的欧拉算子及其逆算子就可构造所有的基于复形的非流形形体，但为有效描述高层运算，文献[7]使用了17个扩展欧拉算子，用其描述局部操作和布尔运算。这种表示方法在几何拓扑层次与放射边数据结构相同，将线框、表面、实体模型在复形层次统一，在壳和环层次描述各维几何元素出现的非流形形状。

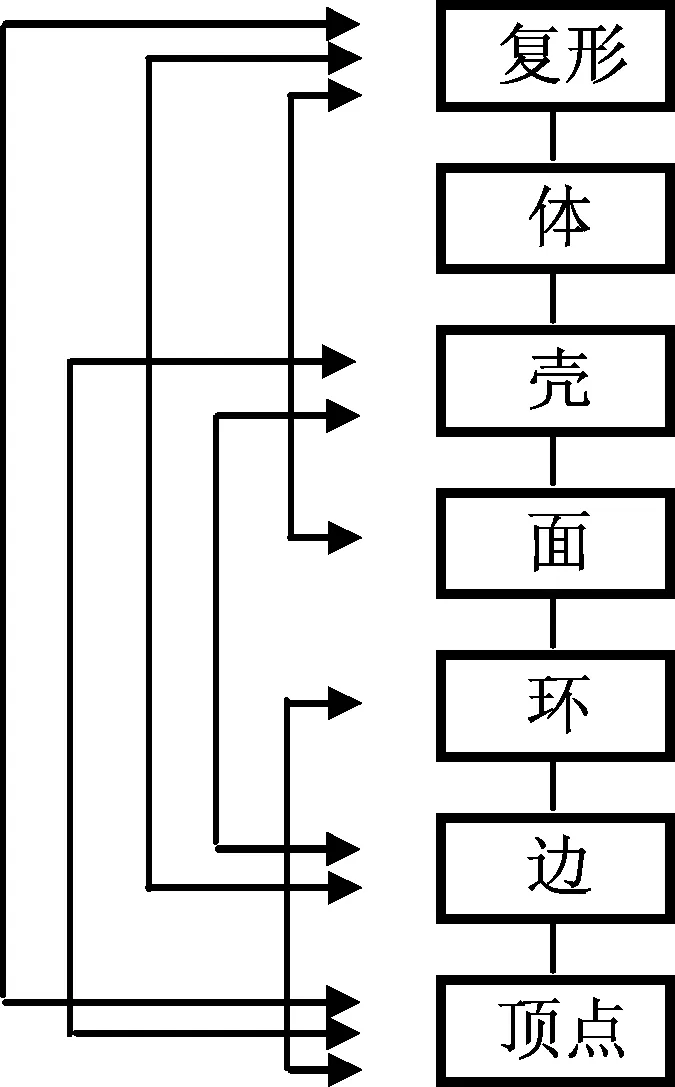
图1 基于复形的层次结构Fig.1 Architecture based on complex

1.5粘合边数据结构

文献[8]将代数拓扑中复形的概念和方法引入非流形表示，给出了非流形的一个严格的数学定义，说明复形统一了三种模型，即零维骨架为全部顶点，一维骨架为棱集合+悬点(线框模型)，二维骨架为面集合+悬边+悬点(表面模型)，三维骨架为三维实体(实体模型)。文献[8]扩展了放射边数据结构，提出了一种粘合边数据结构，其中每条边有多个粘合边，每个粘合边由2条有向边组成。操作分为基本操作和高级操作两种：基本操作包括生成单形、粘合及分离操作、扩展的欧拉操作等；高级操作包括扫描操作、驱动操作、分裂操作、布尔操作等。这种表示方法将非流形形体按复形进行描述，使非流形形体的表示有坚实的数学基础。

上述各种非流形形体的边界表示方法中，除半边数据结构外，其余表示方法都实现了线框、表面、实体模型的统一。就该意义来说，它们是一致的，但其各自能表示的非流形形体和处理方法却存在差异。放射边数据结构及其变形的非流形形体覆盖域最广，是以面边和点边对作为其核心，重点是点边，目的是为了表示一般的非流形形体。半边数据结构是将有限的非流形形体按特殊情况或伪流形表示，目标是为实现操作的便利。混合边数据结构主要是为统一3种模型，形体的表示限于正则形体，以代数拓扑中的复形概念为基础，构造非流形模型，能在确定的表示域上统一线框、表面和实体模型，又使之具有坚实的数学基础。此外，拓扑数据结构作为几何造型的关键部分，其运算效率及存储空间严重制约造型系统的功能和效率。

2 非流形结构

2.1拓扑结构

图2 拓扑结构Fig.2 Topological structure

将代数拓扑中的单纯复形和CW复形的概念和方法引入几何造型系统中，建立以复形为基础的统一的产品模型[9-11]。该模型的拓扑关系由复形中的邻接关系决定，复形的定向决定模型中拓扑元素的方向，如图2所示。模型的表示域为复形的伴随多面体，此处多面体的概念与传统的不同，根据代数拓扑学中复形理论可知：其表面可为复杂曲面。模型中的边界采用以边为基础的B-rep表示，定义一个引用边结构存储边的一个或若干个副本，并存储方向，这样就可表示出多个面共享一条边的非流形结构，本文称该结构为引用边结构。引用边结构能表示物体的悬面、悬边、悬点等情况，以及物体的内部结构，它将一条边的拓扑结构刻画成2个层次，表示的拓扑元素间的逻辑关系简洁、自然、直观，人为因素少。同理定义引用面与引用点，将复形作为基本结构，有效而无二义性地表示了非流形结构。

2.2数据结构

形体在计算机内部的表示就是几何造型的数据结构。数据结构是几何建模的关键，直接影响整个CAD系统的功能效率。好的拓扑关系的数据结构应能完整无二义性地定义几何实体；能方便快捷地访问相关数据；作为CAD系统的底层支持，应为用户提供功能强大而完备的技术支持和完善的产品信息。现有的数据结构都未有效结合完整表示非流形几何模型及减少存储数据、提高运算效率，为此本文提出了一种基于复形的改进非流形数据结构，如图3所示。图3中：虚线框中的结构体是从其上实线表示的结构体派生出的。在数据结构设计中，尽量避免信息的重复存储以求实现优化。在拓扑结构的面、边、点结构中均存储了该拓扑结构的几何指针，使拓扑信息与几何信息建立起关联。

本文数据结构的特点如下。

a)拓扑信息与几何信息分离，便于具体查询各元素，获取其信息；便于支持各种局部操作。

b)采用代数拓扑学中的复形结构，使非流形的表示有坚实的数学基础，可统一表示线框、表面和实体。

c)由于采用复形为基础的结构，既允许标准的集合运算，又允许正则的集合运算。

d)采用面向对象的设计方法，使用类的继承与派生，减少了数据存储量，便于运算。

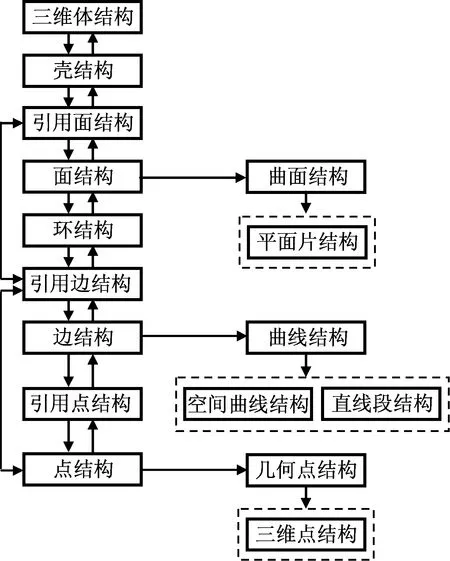
图3 非流形数据结构Fig.3 Non-manifold data structure

e)结构中的各元素链表均采用双链表的存储结构，适应了面表、边表等信息频繁修改的需要。

在图形软件中显示的四种典型非流形形体如图4所示，该软件的图形拓扑结构采用了本文的数据结构。

在不同软件中，四组流形形体应用程序内存占用如图5所示。图5中：软件1采用本文提出的数据结构；软件2为金属3D打印专用软件AutoFab。

图4 典型非流形形体显示Fig.4 Typical non-manifold modeling view

图5 不同软件流形形体应用程序内存占用

3 支持非流形结构的欧拉算子

3.1欧拉运算理论基础

传统的Euler算子不适于非流形物体，在代数拓扑中引入扩展的Eule-Poincare公式

v-e+(f-r)-(V-Vh+Vc)=

C-Ch+Cc

(1)

式中：v，e，f，V，C分别为点数、边数、面数、体数和复形数；r为环数；Vh，Vc，Ch，Cc分别为体的通孔数、体的穴数、复形的通孔数和复形的穴数。非流形几何造型的拓扑算子及其逆算子为扩展的Euler算子，式(1)也成为检验非流形合法性的依据。

3.2扩展欧拉运算

理论上，只需9种欧拉运算和其逆运算就可定义所有基于复形的非流形模型。但在实际应用中，为描述更高级的运算，常需要更多的欧拉运算。非流形模型的15种扩展欧拉算子，如图6所示[3]。图6中：体中的穴(cavity)和通孔(hole)分别定义为Vcavity，Vhole，同理复形中的穴和通孔被定义Ccavity，Chole。对更高级的欧拉运算，可用一系列图6的基本运算完成。

图6中箭头表示运算方向，括号中为逆运算标。Make，kill均为一种操作，下划线后的vertex，edge，……等拓扑元素是操作的对象。如第6种欧拉运算的正运算表示的是生成一条边，删除一个环。其他运算类似。

4 结束语

拓扑数据结构是3D打印技术中几何建模的关键部分，其优劣直接影响整个打印系统的功能和效率，因此功能、效率、存储空间间构造最优的拓扑数据结构尤为关键。本文对一种表示流形形体和非流形形体的统一数据结构进行了研究，提出了基于复形的改进非流形模型数据结构，利用引用面、边及点结构可完整地表示非流形几何模型，实现线框、表面、实体和自由曲面模型的统一，同时采用面向对象的设计方法，使用类的继承与派生，减少了数据存储量，提高了存储和运算效率。给出的欧拉算子可为更高级的欧拉操作和布尔操作提供基础，对3D打印模型发展有一定参考意义。后续可考虑数据结构的融合，提高数据存储效率，减少内存用量。

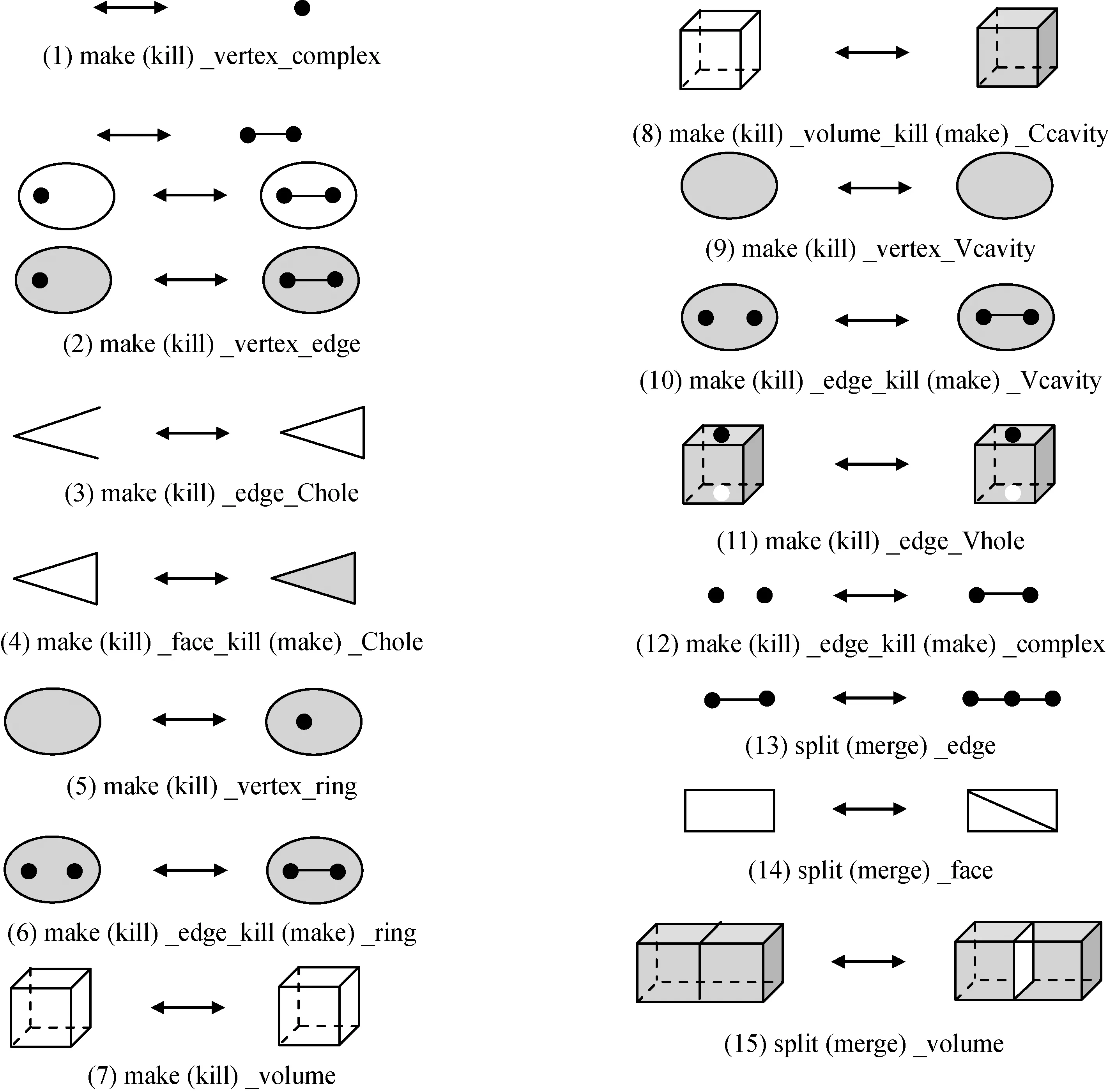
图6 扩展的支持非流形结构的欧拉运算Fig.6 Extended Euler algorithm supporting non-manifold structure

[1] MANTYLA M. An introduction to solid modeling[M]. New York: Computer Science Press, 1988.

[2] REQUICHA A A G, ROSSIG NAC J R. Solid modelling and beyond[J]. IEEE CG & A, 1992, 12(5): 31-44.

[3] GUÉZIEC A, TAUBIN G, LAZARUS F. Cutting and stitching: converting sets of polygons to manifold surfaces[J]. IEEE Transactions on Visualization and Computer Graphics, 2001, 7(2): 136-150.

[4] 孙家广, 杨长贵. 计算机图形学[M]. 3版. 北京: 清华大学出版社, 1998.

[5] WEILER K J. Topological structures for geometric modeling[D]. New York: Rensselaer Polytechnic Institute, 1986.

[6] KALAY Y E. The hybrid edge: a topological data structure for vertically integrated geometric modeling[J]. CAD, 1989, 21(3): 130-140.

[7] MASUDA H. Topological operators and boolean operations for complex—— based on manifold geometric models[J]. CAD, 1993, 25(2): 119-129.

[8] 武仲科, 吴骏恒. 用复形方法建立统一的产品模型——关于下一代造型系统的研究[J]. 航空学报, 1995, 16(6): 662-670.

[9] 聂灵沼, 丁石孙. 代数学引论[M]. 北京: 高等教育出版社, 1998.

[10] 李元熹, 张国栋. 拓扑学[M]. 上海: 上海科学技术出版社, 1986.

[11] 苏竞存. 流形的拓扑学[M]. 武汉: 武汉大学出版社, 2005.

AnUniformDataStructureSupportingManifoldandNon-ManifoldModeling

ZHANGCheng-lin1，ZHULin2，WENShan-shan3，WANGZhuo3，WANGLian-feng3

(1. School of Engineering Science, University of Science and Technology of China, Hefei230026, Anhui, China;2. School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai200240, China;3. Shanghai Aerospace Equipments Manufacturer, Shanghai200245, China)

To solve the large storage space and low computation efficiency in non-manifold modeling data structure and the limitation in manifold modeling in3D printing, an uniform data structure supporting manifold (regularized) and non-manifold (non-regularized) modeling was studied in this paper. Some boundary representation methods which were half edge data structure, radial data structure, hybrid edge data structure, cell complex and adjunction edge data structure for non-manifold modeling were analyzed. It found that the present data structures did not put effectively expressing non-manifold model, reducing data storage and improving operational efficiency together. So the data structure for non-manifold modeling based on complex was put forward. The geometrical model of non-manifold is represented completely through face, edge and vertex by reference, which realizes the uniform models of the wireframe, surface, solid and free curved surface. The object-oriented design is used and successiveness and derivation of class are applied also to reduce the data storage and improve the efficiency of the storage and computation. The extended Euler operator can provide the base for higher level Euler operation and Boolean operation. The unified data structure proposed uses pointer format in data structures of face, edge and vertex to avoid duplicated information. Tests have shown that it can represent the manifold and non-manifold modeling with enlarging domain of traditional3d model and effectively reducing the storage space.

3D printing; geometry model; manifold modeling; non manifold modeling; data structure; topological structure; calculating efficiency; storage space

1006-1630(2017)04-0158-06

2016-09-05；

：2016-10-25

航天先进技术联合研究中心技术创新项目资助(USCAST2015-23)

张成林(1983—)，男，硕士，主要研究方向为增材制造技术、高端智能装备研制。

TP391.73

：ADOI:10.19328/j.cnki.1006-1630.2017.04.019