FY-4A星GIIRS大气温度廓线反演模拟试验研究

鲍艳松，汪自军，陈 强，周爱明，董瑶海，闵锦忠

(1.南京信息工程大学 气象灾害预报预警与评估协同创新中心/气象灾害教育部重点实验室/气候与环境变化国际合作联合实验室/中国气象局气溶胶与云降水开放重点实验室,江苏 南京 210044； 2.南京信息工程大学 大气物理学院, 江苏 南京 210044； 3.上海卫星工程研究所,上海 201109； 4.上海航天技术研究院,上海 201009)

FY-4A星GIIRS大气温度廓线反演模拟试验研究

鲍艳松1,2，汪自军3，陈 强3，周爱明3，董瑶海4，闵锦忠1

(1.南京信息工程大学 气象灾害预报预警与评估协同创新中心/气象灾害教育部重点实验室/气候与环境变化国际合作联合实验室/中国气象局气溶胶与云降水开放重点实验室,江苏 南京 210044； 2.南京信息工程大学 大气物理学院, 江苏 南京 210044； 3.上海卫星工程研究所,上海 201109； 4.上海航天技术研究院,上海 201009)

结合全球大气晴空训练样本(CIMSS)数据，利用辐射传输模式，模拟获得干涉式大气垂直探测仪(GIIRS)亮温资料，结合人工神经网络反演方法，研究了风云四号(FY-4)卫星高光谱红外载荷大气温度反演方法，并研制了全圆盘和中国区域两套大气温度反演模型。反演试验结果表明：对流层大气温度反演精度明显高于平流层，以中国区域反演模型为例，对流层和平流层大气温度反演均方根误差(RMSE)分别为0.846，2.020 K，平均误差分别为-0.003，0.024 K；比较中国区域和全圆盘大气温度廓线反演精度，中国区域大气温度精度明显高于全圆盘，0～70 km处大气温度反演的均方根误差分别为1.922，2.630 K；与欧洲极轨卫星(Metop-A)IASI数据的温度廓线反演结果比较，FY-4A星GIIRS的温度反演精度在低层(>500 hPa)(RMSE=0.790 K)优于IASI(RMSE=0.976 K)，在高层(<500 hPa)(RMSE=1.803 K)低于IASI(RMSE=0.899 K)。研究对FY-4卫星GIIRS的大气温度廓线反演及其应用有重要的参考价值。

FY-4卫星； 干涉式大气垂直探测仪(GIIRS)； 神经网络； 温度廓线； 反演； 对流层； 平流层； 中国区域； 全圆盘

0 引言

大气温度是数值天气预报模式的重要输入数据，对提高数值天气预报精度有重要意义。气象卫星能探测大气辐射，其辐射率数据可反映大气的温度状态。1987年世界气象组织评估了卫星大气探测资料(TOVS)应用对天气预报准确率提高的贡献，提出只有当全球大气温度、水汽探测精度达到无线电探空的水平，才可能对天气预报做出重大改进[1]。这就要求对流层大气温度探测均方根误差小于1 K，大气垂直探测分辨率达到1 km。为实现更高垂直分辨率探测，美国NASA构建了新一代全球环境监测系统NPP(NPOESS Preparatory Project)，对大气温湿卫星探测给出了明确要求：对地表至500 hPa的高度范围内温度和湿度的观测精度分别为1 K和10%，且垂直分辨率为0.3～0.5 千米/层；对500～300 hPa的高度范围内温度和湿度的观测精度分别为1 K和10%，且垂直分辨率为0.5～1.0千米/层；对300～100 hPa的高度范围内温度和湿度的观测精度分别为1 K和20%，且垂直分辨率为1.0～2.0千米/层；对100 hPa以上的高度范围内温度观测精度为1 K，垂直分辨率为2.0～3.0千米/层[1]。我国FY-4卫星2010年立项，2016年FY-4A星发射成功。这些卫星装载的高光谱红外载荷为数值天气预报提供了重要数据。

利用卫星辐射探测大气参数研究始于20世纪中期。1956年KING较早提出根据卫星热红外辐射的观测推算大气温度廓线[2]。其后，随着高光谱遥感技术的发展，AIRS，IASI，CrIS等红外高光谱传感器的在轨运行，大气温度廓线卫星遥感反演方法不断发展[3-5]。这些反演算法可分为统计回归、物理和统计-物理反演法三类，不同反演技术的特点各异。比较分析统计回归反演法、基于变分理论的物理反演法，以及人工神经网络反演法三种主要的反演算法，发现统计回归反演算法虽然计算简便且反演过程稳定，但不考虑大气辐射传输过程，反演精度有待进一步提高；基于变分理论的物理反演法建模复杂，要求初始场，计算量大，需不停的迭代；人工神经网络反演法具很强的非线性表达及良好的容错能力。为此，本文选用人工神经网络法建立反演模型，研究FY-4卫星高光谱红外资料大气温度廓线反演方法。

人工神经网络(ANN)是由大量计算单元构成的非线性系统，它模仿人脑神经系统接收、处理、存储外界信号，具强大的智能处理信息的功能，有非线性映射能力，善于从输入和输出信号中寻找规律，无需精确的数学模型，并行计算能力强，易于软硬件编程计算[6]。在如今的气象领域中，降水预报、雾预报、温湿廓线反演研究等都越来越多地引进了神经网络方法[7-8]。文献[9]用人工神经网络技术反演大气温度的数值模拟，与线性统计算法比较，发现近陆面的温度反演结果优于近海面，且对有较厚逆温层结构的温度廓线，神经网络反演对廓线的复现能力优于线性统计反演。文献[10]用人工神经网络对晴空条件下AIRS模拟辐射值进行大气温度廓线的反演，发现相比于特征向量统计法，神经网络反演方法反演精度更高，误差更小，获得了较好的反演结果。文献[11]用BP神经网络反演12通道地基微波辐射计数据的大气温湿廓线，发现反演结果较其自带的RadiomeNN算法更接近于探空真值。文献[12]用神经网络算法进行AIRS资料的大气温度廓线反演，获得了垂直分辨率1 km的对流层温度反演精度。文献[13]用BP神经网络反演微波辐射计资料的0～10 km高度58层的大气温度，与探空资料及微波辐射计二级产品对比，分析发现大气温度均方根误差范围为1.0～2.0 K。

我国新一代静止气象卫星——FY-4卫星搭载的干涉式大气垂直探测仪(GIIRS)可每15 min提供1次分辨率10 km的大气温度相关数据，在数值天气预报中有重要的应用前景。本文基于辐射传输模式和神经网络反演算法原理，用FY-4卫星高光谱红外探测仪模拟资料，对大气温度廓线反演方法进行了研究。因廓线垂直分辨率高，样本数量庞大，网络收敛慢，寻求合适的网络反演大气温度廓线是本文的研究重点和难点。

1 研究数据及辐射传输模式

1.1研究数据

本文所用的全球大气晴空训练样本(seebor V5.0)是由美国威斯康星大学开发，共由全球范围内晴空条件下15 704条大气温度、湿度和臭氧廓线组成，大气廓线从1 100～0.005 hPa共分成101层，包括NOAA-88、ECMWF 60 L、TIGR-3、臭氧探空值(来自NOAA-8 CMDL)，以及无线电探空值(沙漠地区)等五类有代表性的资料，样本廓线的全球分布如图1所示。其廓线样本大致均匀分布在全球区域，海洋上分布较陆地稀疏，而臭氧和无线电探空值针对的是沙漠地区，分布较集中。

本文研究所用卫星资料为FY-4A星GIIRS资料。FY-4A星于2016年12月11日发射，是我国第二代静止轨道气象卫星的首发星，该星首次搭载了GIIRS。GIIRS采用二维扫描镜+离轴三反射主光学系统收集地气能量，由动镜式傅里叶干涉仪进行探测。扫描系统作步进-驻留扫描，选取所需探测的区域，将地球的大气辐射折射向望远镜主镜。GIIRS气象数据及产品主要有4级，包括0级数据(地面数据接收并转发给资料处理和服务中心进行质量检测、解码、重复资料提出等处理后的资料)、1级数据(0级数据经过预处理系统的定位、定标后形成的资料)、2和3级产品(1级数据经过产品生成系统加工处理生成轨道和侯、旬、月等气候合成产品)[14]。GIIRS的光谱范围为4.4～14.2 μm，试验星的指标低于业务星，试验星和业务星的光谱分辨率分别为0.8/1.6，0.625/1.2 cm-1，星下点空间分辨率相应分别为16，8 km，探测地域可控。GIIRS 高光谱红外探测仪的性能特性和主要探测目标分别见表1、2[2]。

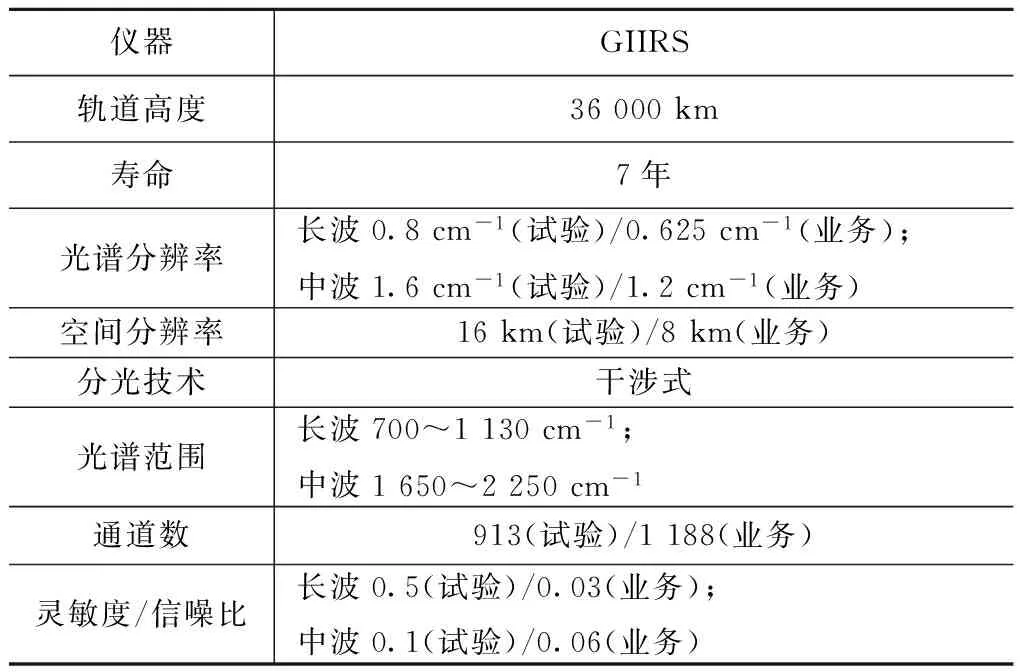
表1 GIIRS性能特性

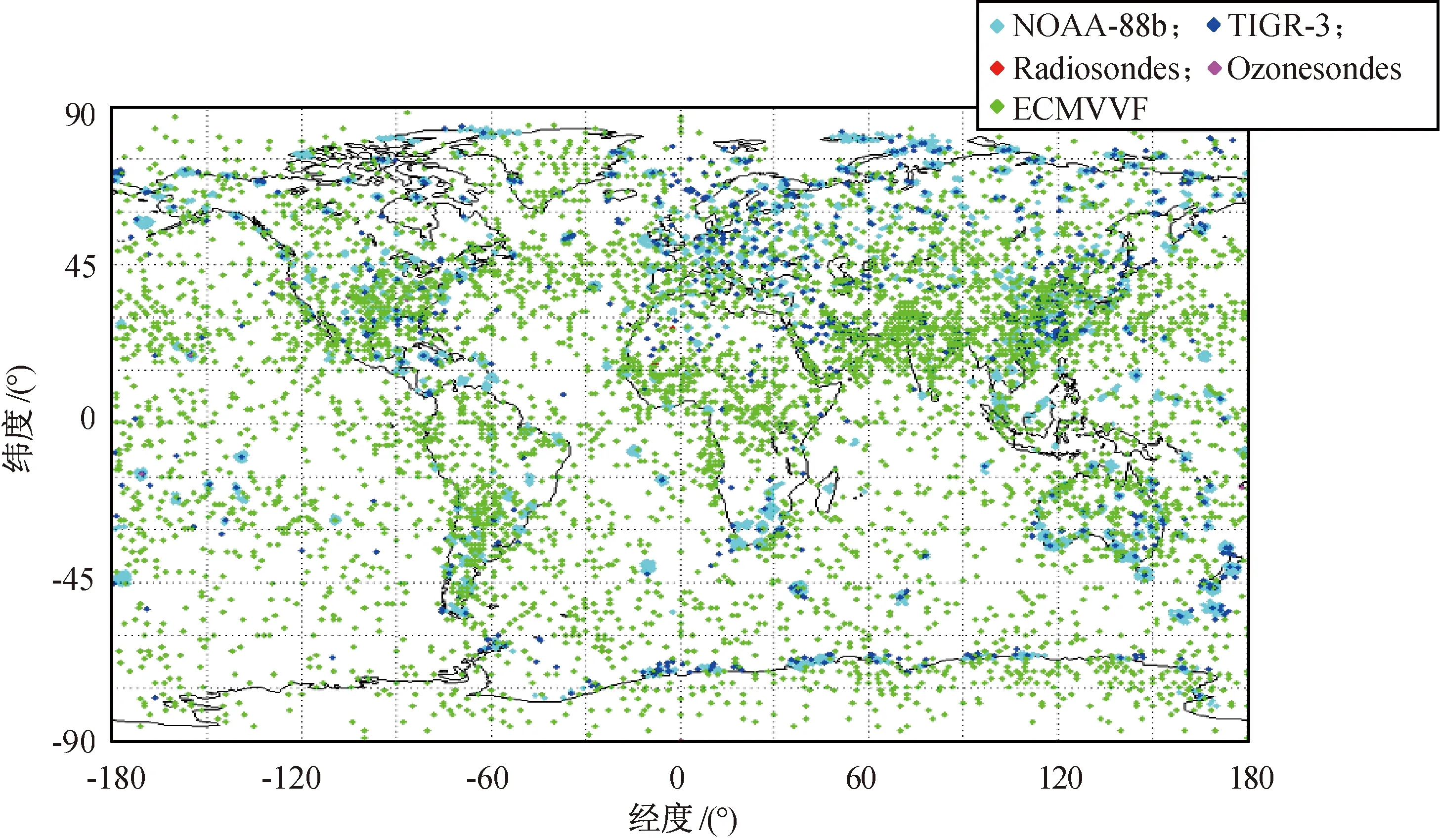
图1 15 704个样本廓线全球分布Fig.1 Global distribution of 15 704 profiles

光谱范围/cm-1主要探测目的700～790温度廓线探测,利用对冷目标和云顶高度的敏感性,进行部分云存在时的温度廓线反演790～1130表面和云特性,O3探测1210～1650水汽、温度廓线探测,N2O、CH4和SO2探测2100～2150CO总量2150～2250温度廓线探测,N2O总量

1.2模型

本文使用的FY-4A星GIIRS辐射传输模式(RTM)由威斯康星大学空间科学与工程中心的WEISZ开发，该模式可用于云雨和晴空条件下的红外波段亮温模拟。本文针对的是晴空模式下的亮温值的模拟计算，故正演模式是在原有的基础上修改，并在LINUX系统中编译、运行晴空条件下的亮温值。

该辐射传输模式中的快速模型系数是由对一个0.1 cm-1逐行计算透过率数据(LBLRTM v11.6)和特定的光谱响应函数(由NSMC提供)获得LBL特定的仪器的透过率而计算出的，再通过回归分析，获得晴空、臭氧，以及水汽条件下的快速模型系数。逐线模式可用于计算一个体积庞大的气层单色光学厚度查找表。模式中使用的快速算法PFAAST(Pressure Layered Fast Atmospheric Transmittance)是由HANNON，STROW，MCMILLAN共同开发，适于各种分辨率的高光谱传感器。

FY-4A星正演模拟的输入参数包括大气和地表两部分。大气的输入数据包括101层(0.005～1 100 hPa)气压分层数据、101层大气温度，以及101层大气湿度廓线信息；地表输入数据包括地表温度、地表压强，以及陆地所占比例，模式中默认所有通道的地表比辐射率0.98，且将模式底层的压强和温度分别表示为表面压强和温度。

2 神经网络反演算法

2.1网络结构

本文用反向传输神经网络(BP)对大气温度进行反演建模。BP神经网络包括输入层、隐含层和输出层，可有效用于复杂非线性函数的逼近，能实现任意精度的连续函数映射。BP神经网络模型如图2所示。

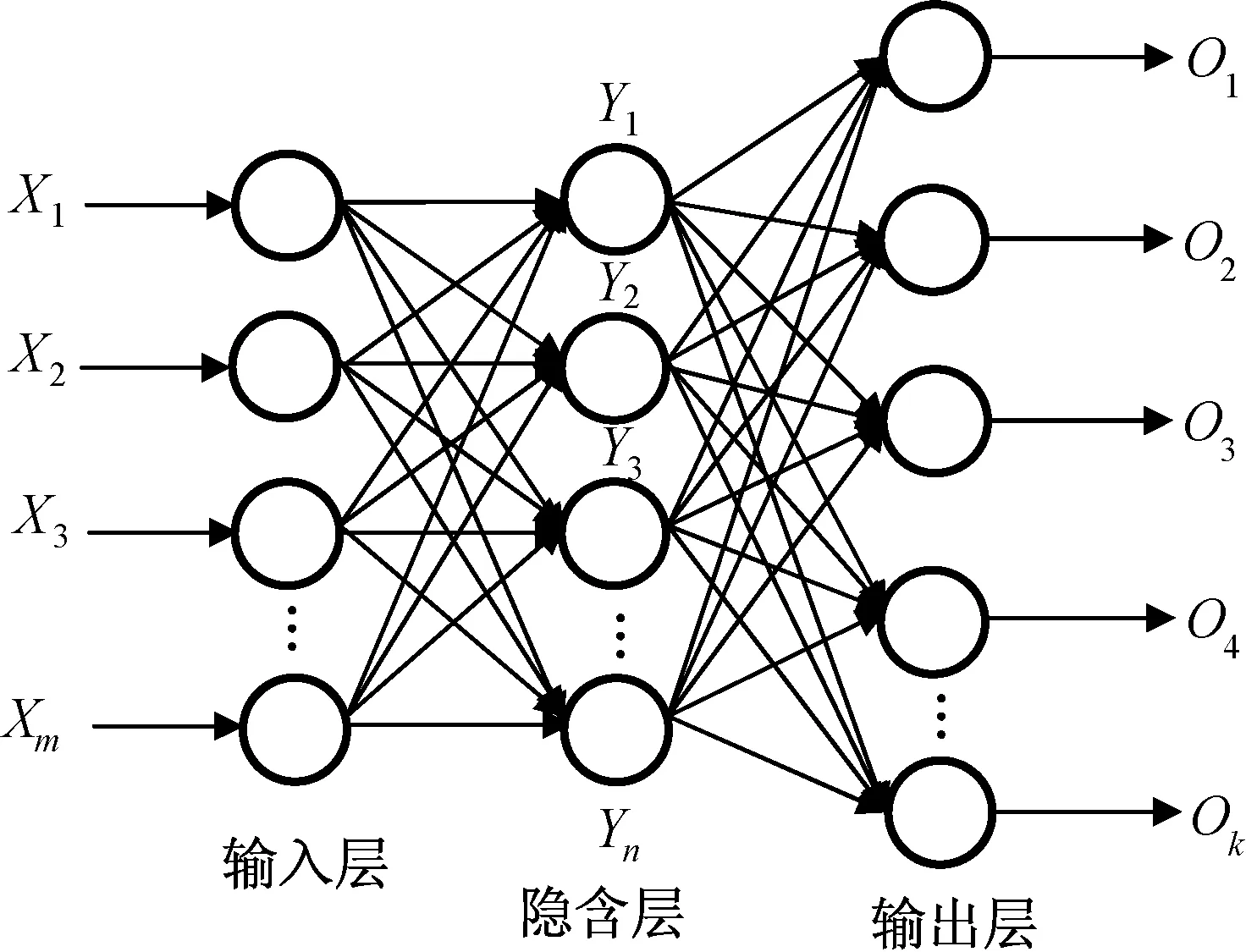
图2 BP神经网络结构Fig.2 BP neural network

神经网络模型的输出

O=f2(Yv+b2)

(1)

Y=f1(Xw+b1)

(2)

式中：O为网络的输出；X为输入层，Y为隐含层的输出；v为隐含层至输出层的连接权系数阵，初始时刻为一组随机数；w为输入层至隐含层的连接权系数阵，初始时刻为一组随机数；b1，b2分别为隐藏层和输出层单元偏置值阵；f1，f2为神经元的非线性作用函数，能依每层设定，可取正切[10]。

用4种精度评价方法评价大气温度廓线反演精度：均方误差(MSE)σMSE、相关系数R、均方根误差(RMSE)σRMSE和平均误差(ME)σME。定义分别为

σMSE=E(e2)=E((t-o)2)

(3)

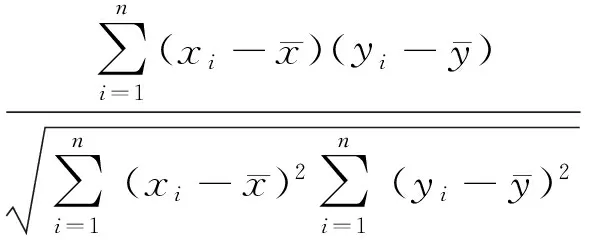
(4)

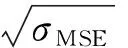
(5)

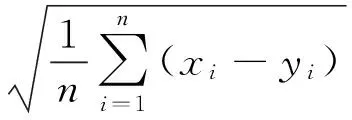
(6)

式中：t为期望输出；o为实际输出；e为绝对误差；n为样本廓线数；xi为用BP神经网络反演得到的大气温湿廓线值；yi为实际的大气温湿廓线值。

2.2输入层和输出层设置

用辐射传输模式模拟计算出的亮温值对应的是FY-4A星GIIRS的913个通道的亮温值，反演101分层上的温度和湿度值，因此用BP神经网络的输入是913个模拟亮温值，输出层则是101个大气温度和湿度垂直廓线，训练和测试的样本由GIIRS的15 704个通道亮温值和相应的温度与湿度廓线对组成。对如此庞大的量实施网络训练并要得到最优网络，难度很大，网络输入量大，会导致结构冗余、耗费时间长及泛化性能不高。

考虑到913个亮温值存在一定的相关性，基于主成分分析法实现系统降维和特征提取，对FY-4A星GIIRS的913个通道的观测值取其前40个能表示99.998 8%的全部通道信息量的主成分[15]。将40个通道的亮温值作为网络的输入参数，即输入层有节点40个。将通过主成分分析后的资料用于大气温湿廓线反演研究有其明显的优越性，因其保留与反演量相关性高的主分量，且主分量间是正交的，故不受累赘反复的信号噪声影响。

2.3隐含层设置

网络特性易受其隐层节点数的设置影响。若隐含节点数太少，使信号资料不足，则会影响网络的效果；若隐含节点太多，则会使训练花费更多的时间，降低计算效率[16]。综合考虑计算效率和反演精度，选用文献[17]提出的方法，BP神经网络隐含节点数

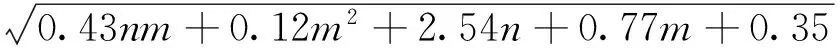
(7)

式中：h为隐含层节点数；n为输入层节点数；m为输出层节点数[18]。最终确定隐含层结点数为56。

2.4传递函数和训练算法选取

神经网络的设置和激活传递函数选用影响神经网络特性。本文用newff函数创立神经网络，用Matlab计算机语言完成程序的编写，神经网络训练参数设置见表3。研究中，选用双曲正切S型传递函数tansig作为激活传输函数，有

O=tansig(W×P+B)

(8)

式中：O为输出值；W为权值；P为输入矢量；B为偏差。

BP神经网络算法中，网络的权值和阈值通常是沿网络误差变化的负梯度方向调节，最终使网络误差达到最小值。几种典型快速学习算法性能比较见表4。考虑本文所用的训练样本大、网络设置参数多、数据存储量大等因素，选用Scaled共轭梯度-trainscg学习算法[4]。

表3 BP神经网络参数值

表4 典型学习算法性能比较

3 反演结果

3.1全圆盘区域大气温度反演结果

3.1.1 整层(0.005～1 100 hPa)大气温度

在全圆盘区域大气温度反演试验中，基于样本数据15 704个，用BP神经网络反演算法，建立温度廓线反演模型。为检验BP神经网络大气温度廓线反演精度，用样本数据6 282个验证反演模型精度，统计大气温度廓线反演值和样本值的相关性、均方根误差和评价误差。温度反演值和样本值散点图如图3所示。由图3可知：反演值与样本值有较高的一致性，反演的温度值与样本值的相关系数0.995，均方根误差2.63 K，平均误差-0.002 K，反演值与样本值均匀分布在直线y=x两侧。

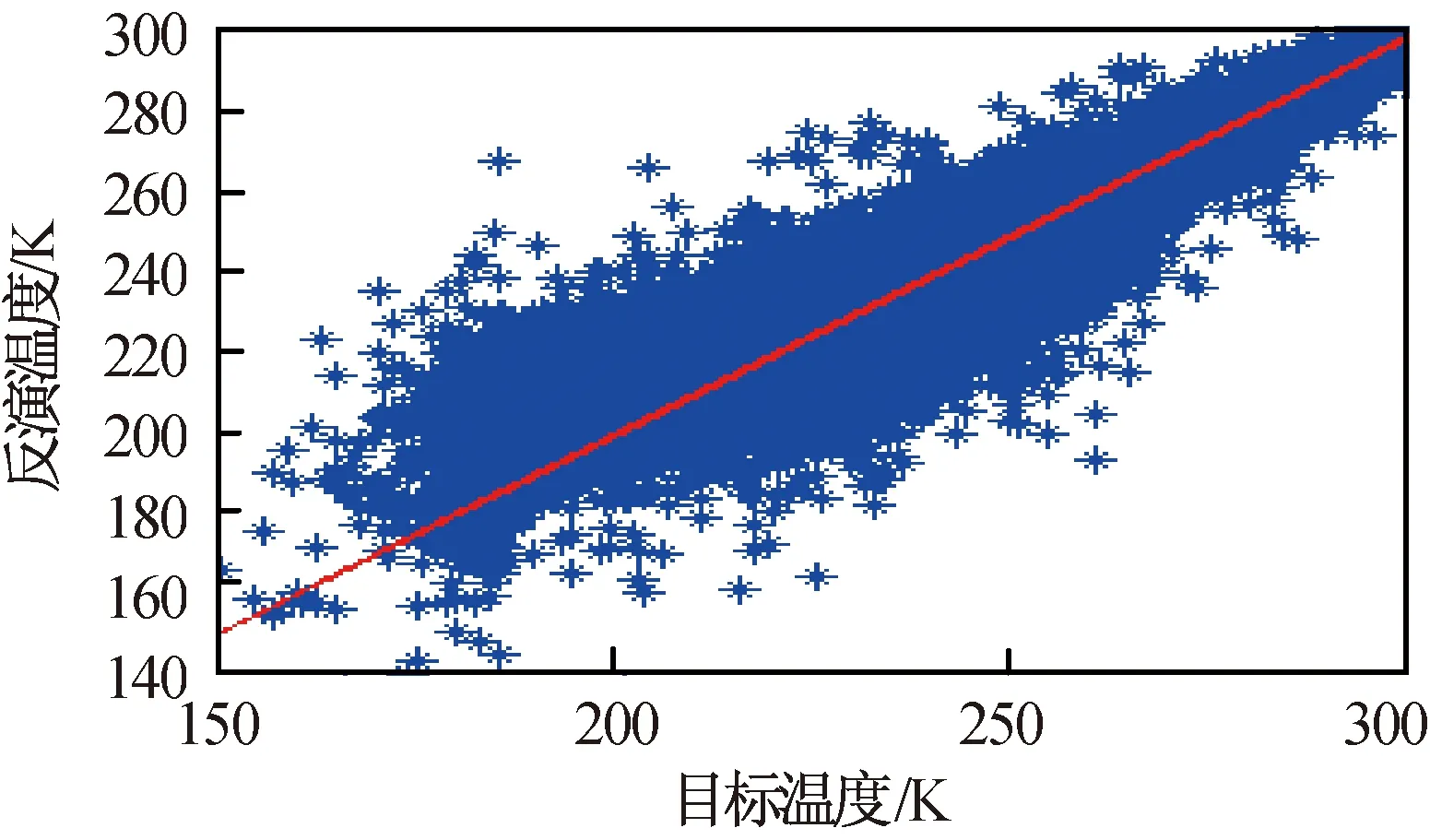
图3 反演温度散点图Fig.3 Temperature scatter diagram of retrieval

样本(东经48.96°，南纬6.13°)廓线图和散点图如图4所示。由图4(a)可知：反演与目标温度值趋势一致，能较好地重合，但在廓线的突变处反演的精度尚待提高。由图4(b)可知：反演与目标温度值的RMSE达到了0.605 K，相关系数0.999，且反演温度值较目标偏高0.099 K。

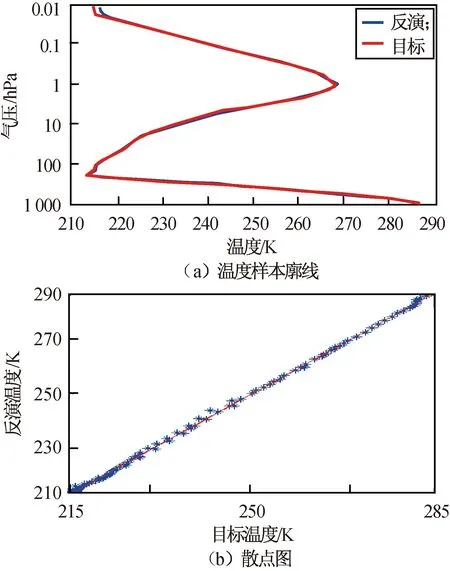
图4 反演温度样本Fig.4 Temperature profile

反演的整层大气温度RMSE如图5所示。由图5可知：分层反演温度RMSE最小值0.494 K；在低层(>1 000 hPa)，反演温度的RMSE平均值0.579 K。

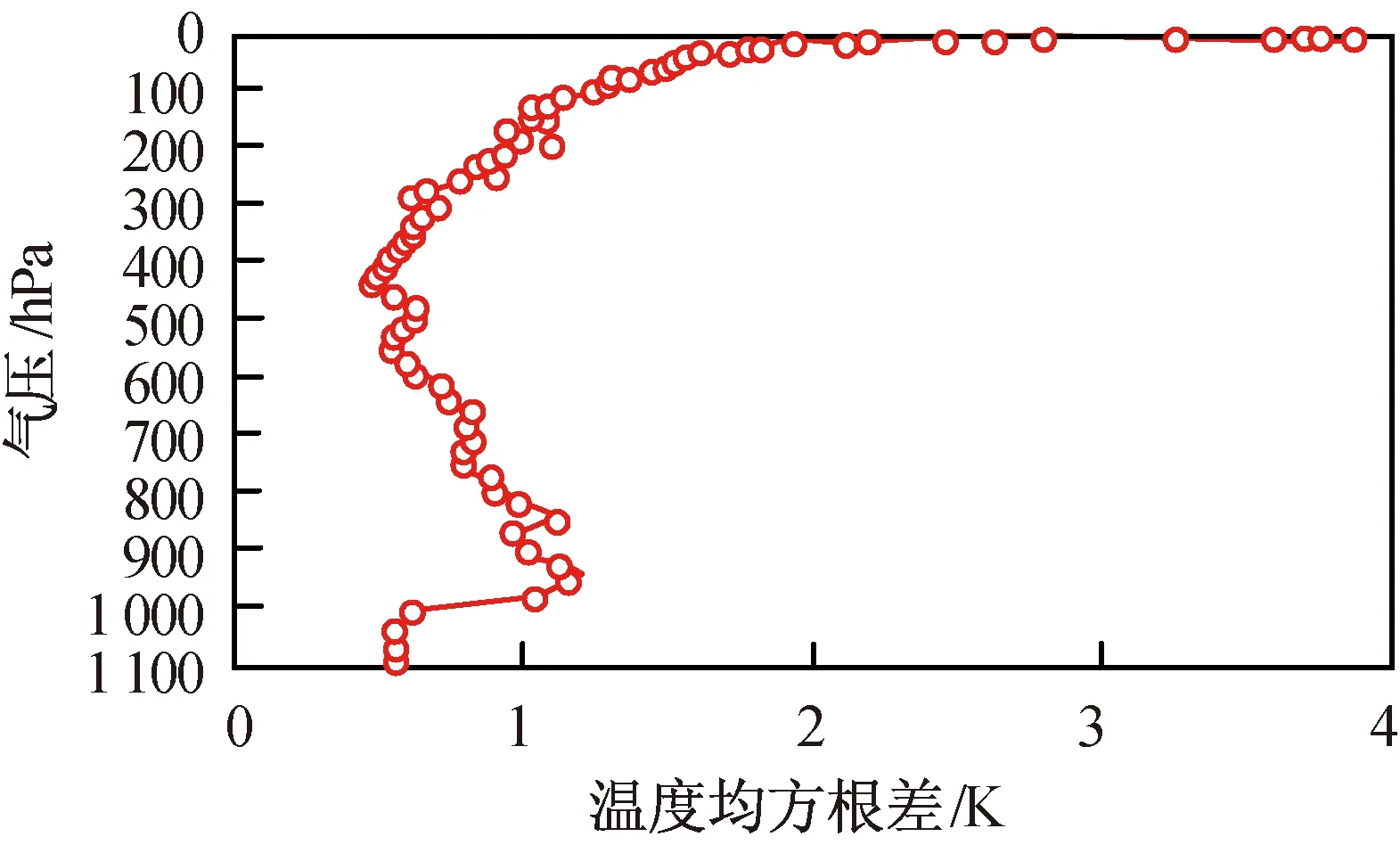
图5 反演整层大气温度RMSEFig.5 RMSE distributions of retrieval temperature from whole layer atmosphere

1～1 000 hPa反演温度的误差分层双纵坐标图如图6所示。图6中：黑色线为目标温度的误差值；红色线为温度反演的误差值。由图6可知：反演温度的误差小于0.12 K，大致均匀分布在黑色线两侧，且低层的温度反演误差小于高层，底层以正作用为主，而高层以负作用为主。总体而言，反演温度的平均误差值在整层大气中均较小，反演温度的精度较好。

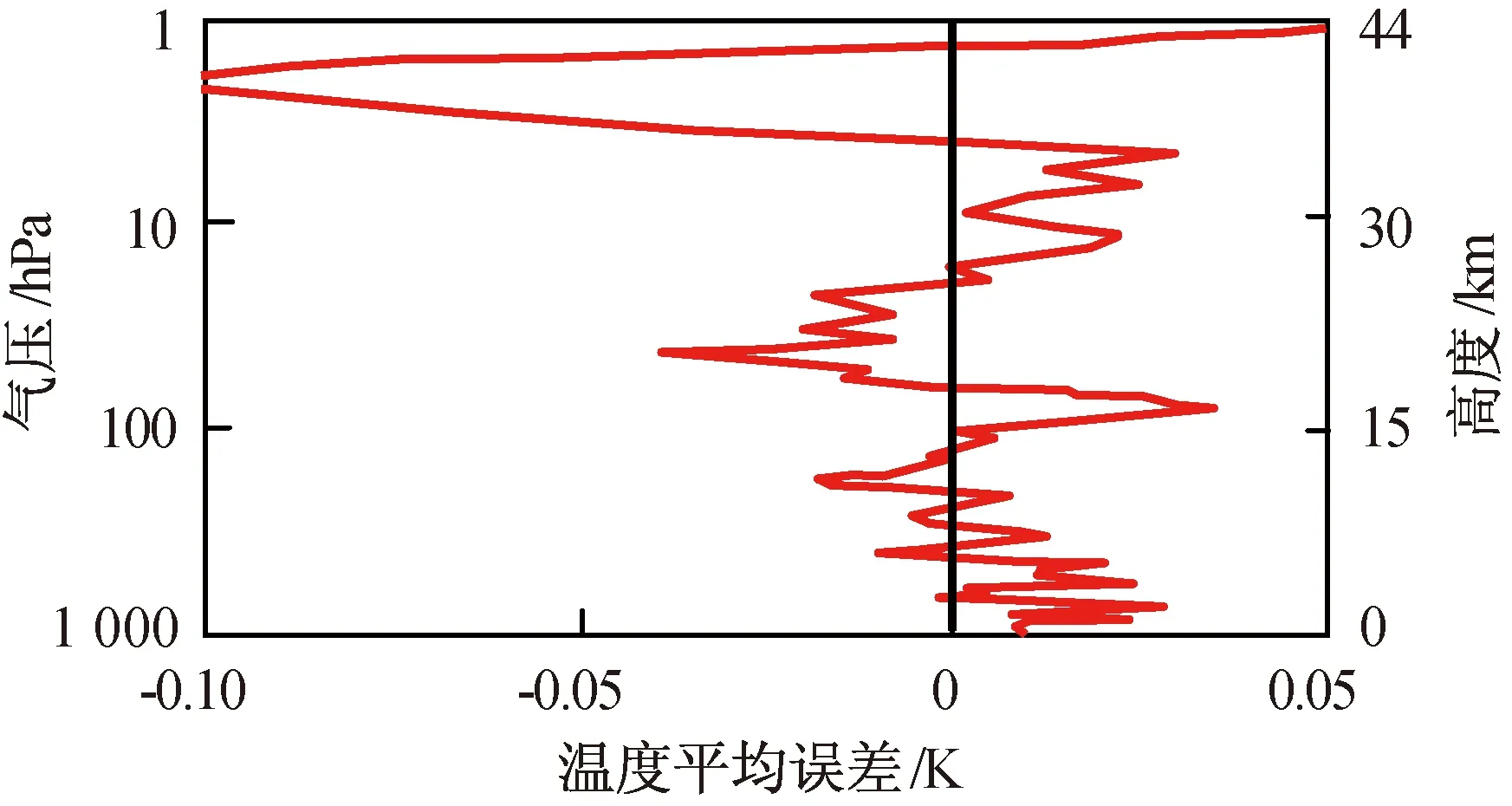
图6 1～1 000 hPa反演温度的平均误差分层双纵坐标图Fig.6 Mean error’s distributions of 1～1 000 hPa temperature retrieval

对整层大气，为检验5类CIMSS数据反演大气温度的效果，分别统计了5类CIMSS数据反演温度的R，RMSE，ME，结果见表5。由表5可知：NOAA-88的CIMSS数据进行大气温度反演的精度最高(RMSE为1.853 K)，平均误差0.070 K，具高度相关性(R=0.998)；TIGR-3数据反演温度的精度差于其他几类，反演温度的RMSE为3.391 K。

3.1.2 对流层(100～1 000 hPa)大气温度

对流层区域温度反演散点图如图7所示。由图7可知：反演值与样本值有较高的一致性，反演的温度值与样本值的相关系数0.995，均方根误差0.852 K，平均误差-0.005 K，反演值与样本值均匀分布在直线y=x两侧。

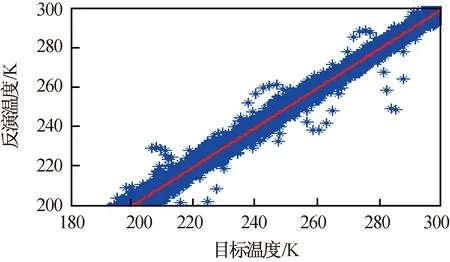
图7 反演温度散点图Fig.7 Temperature scatter diagram of retrieval

反演的对流层大气温度RMSE如图8所示。由图8可知：温度RMSE优于1 K的概率为73.58%，分层温度的RMSE均小于1.247 K，在450 hPa高度出现了RMSE最小值(约0.5 K)，温度反演的精度较高。

3.1.3 平流层(1～100 hPa)大气温度

平流层区域温度反演散点图如图9所示。由图9可知：反演值与样本值有较高的一致性，反演的温度值与样本值的相关系数0.992，均方根误差2.454 K，平均误差0.007 K，反演值与样本值均匀分布在直线y=x两侧。

反演的平流层大气温度RMSE如图10所示。由图10可知：反演温度RMSE优于2 K的概率为58.82%，分层温度的RMSE最小1.258 K。反演温度的RMSE随高度的增加而变大，在20～100 hPa气压高度层间，温度的RMSE为1～2 K。

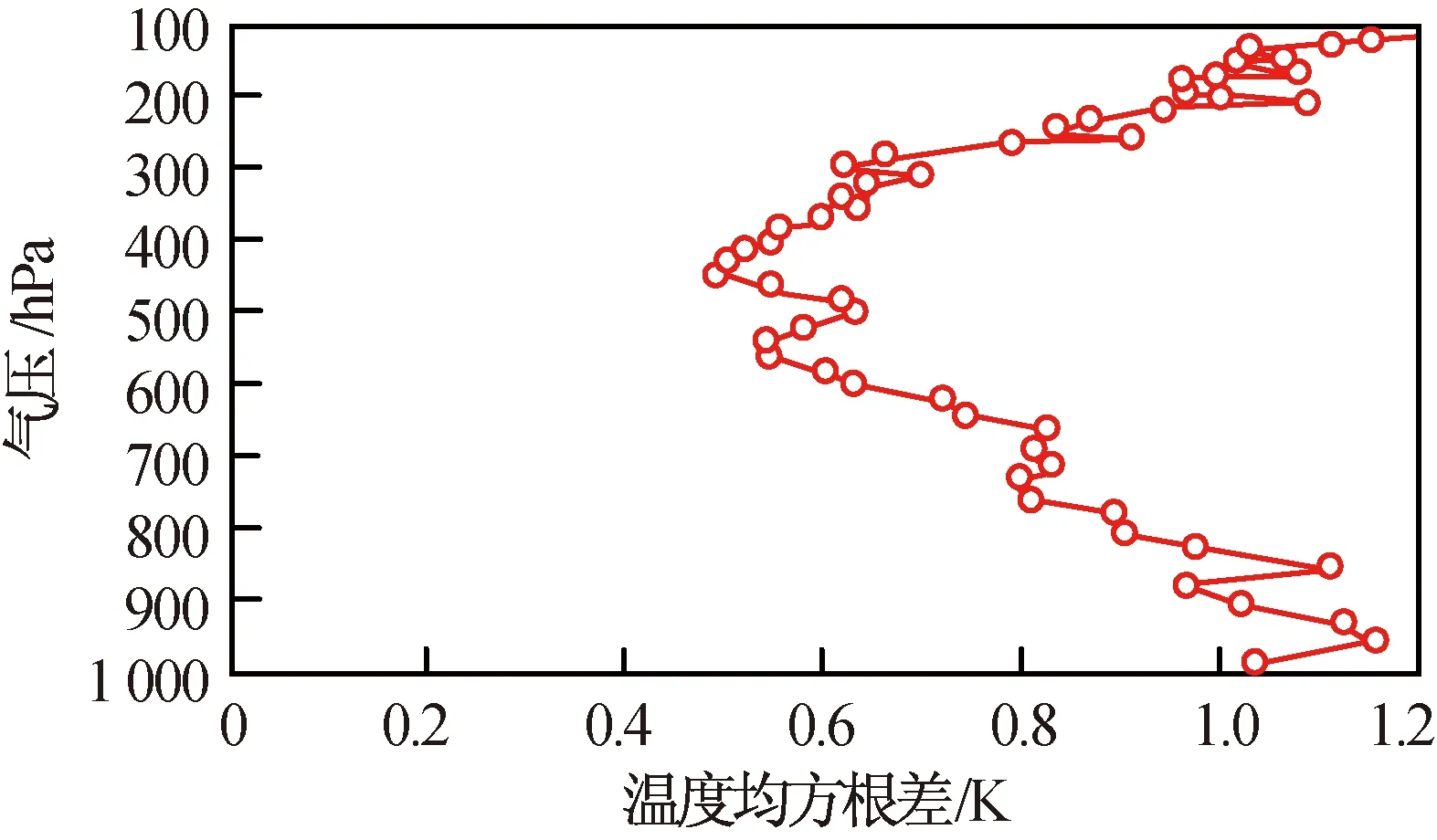
图8 反演对流层温度RMSEFig.8 RMSE distributions of retrieval temperature from troposphere

图9 反演温度散点图Fig.9 Temperature scatter diagram of retrieval

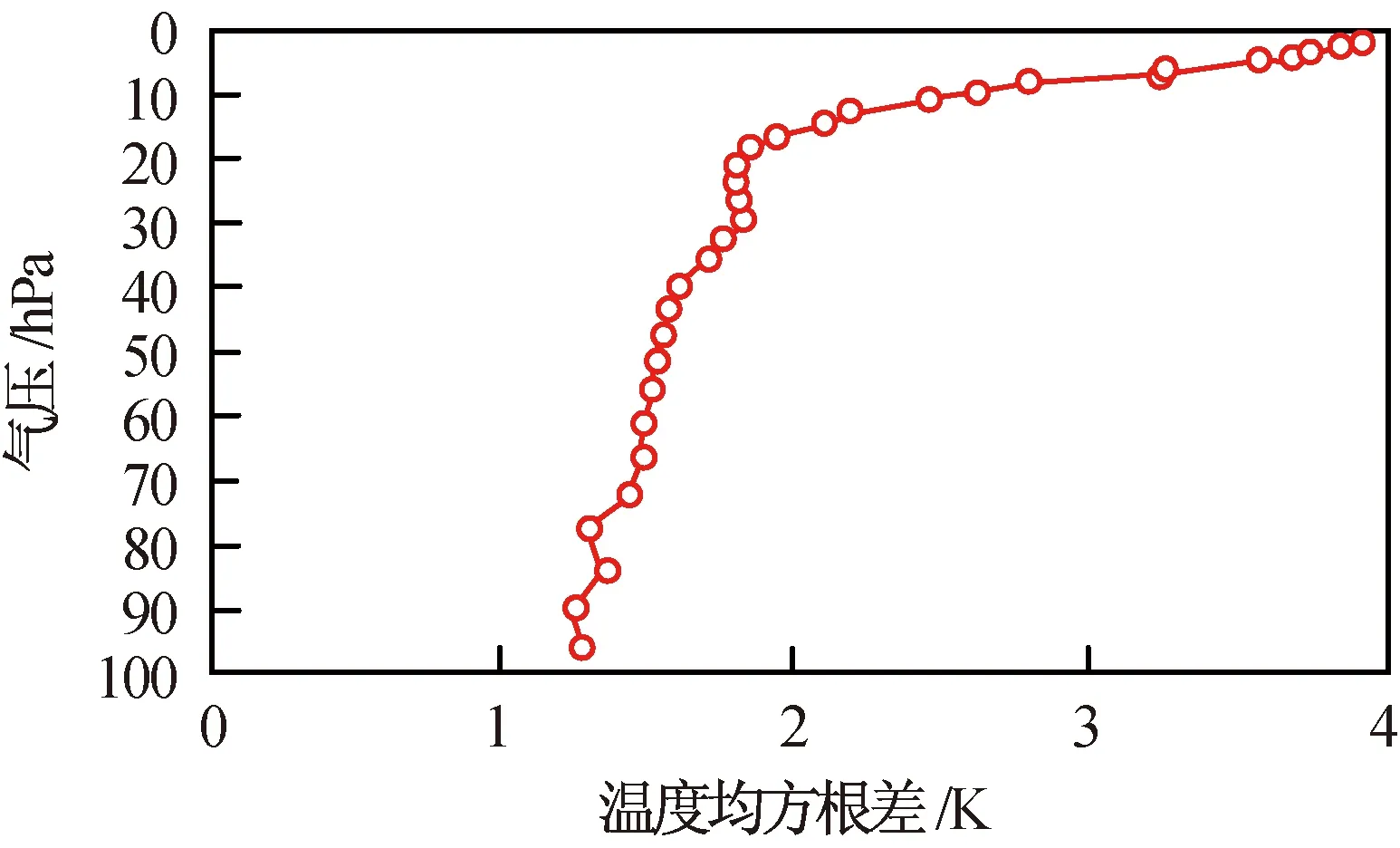
图10 反演平流层温度RMSEFig.10 RMSE distributions of retrieval temperature from stratosphere

表5 5类CIMSS数据反演大气温度统计

3.2中国区域大气温度反演结果

3.2.1 整层(0.005～1 100 hPa)大气温度

中国区域反演温度散点图如图11所示。中国区域共有测试样本廓线576个。由图11可知：反演的温度值与目标值的相关系数0.998，有较高的相关性；整层大气的温度均方根误差1.922 K，反演值较目标温度值偏高0.025 K，反演与观测的温度值均匀分布在直线y=x两侧，有较好的一致性。

图11 反演大气温度散点图Fig.11 Scatter plots of retrieving atmospheric temperature

在综合考虑检验反演效果的廓线576条下，反演的整层大气温度RMSE如图12所示。由图12可知：整层温度反演的RMSE为1.992 K，最小值0.628 K；针对576个测试样本，RMSE最小值0.604 K，此时R为0.999 8，平均误差0.017 K。

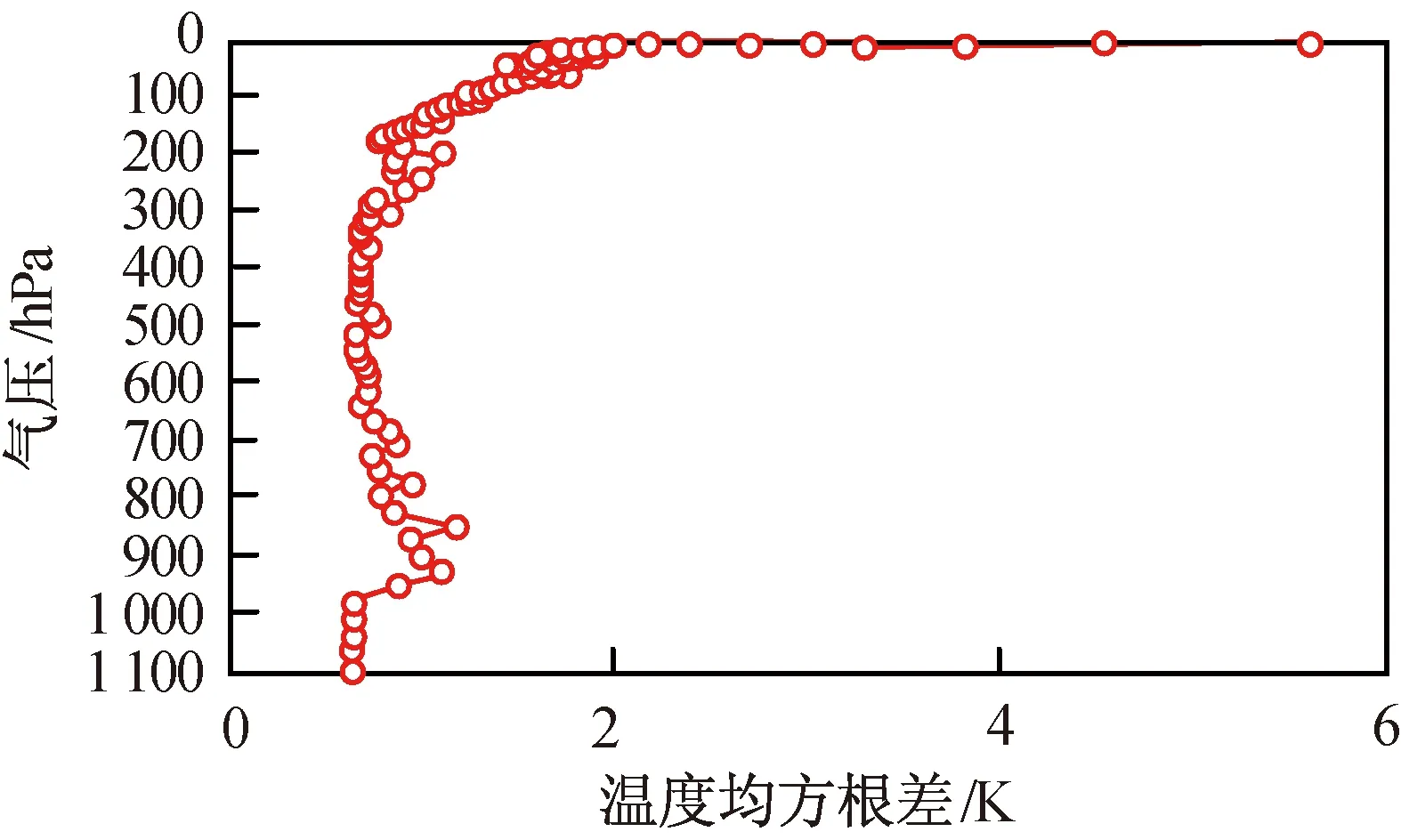
图12 反演整层大气温度RMSEFig.12 RMSE distributions of retrieval temperature from whole layer atmosphere

1～1 000 hPa温度的反演误差分层双纵坐标图如图13所示。图13中：黑线为目标温度的误差值。由图13可知：反演温度的误差范围为-0.160～0.233 K，大致均匀分布于黑线两侧；对流层和平流层大气温度反演平均误差分别为-0.003，0.024 K。

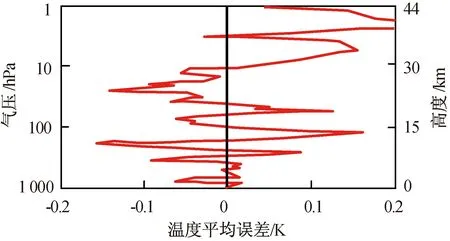
图13 1～1 000 hPa温度的反演误差分层双纵坐标图Fig.13 Mean error’s distributions of 1～1 000 hPa temperature retrieval

3.2.2 对流层(100 hPa～1 000 hPa)大气温度

对流层区域温度反演散点图如图14所示。由图14可知：反演值与样本值有较高的一致性，反演的温度值与样本值的相关系数0.998，均方根误差0.846 K，平均误差-0.003 K，反演值与样本值均匀分布在直线y=x两侧。

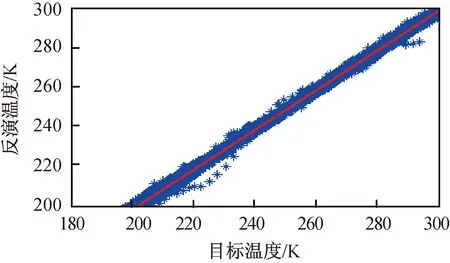
图14 反演温度散点图Fig.14 Temperature scatter diagram of retrieval

反演的对流层温度RMSE如图15所示。由图15可知：对流层区域温度的RMSE为0.846 K，对流层大气温度的探测精度1 K/km，平均误差范围在-0.163～0.163 K，温度RMSE优于1 K的概率79.25%。

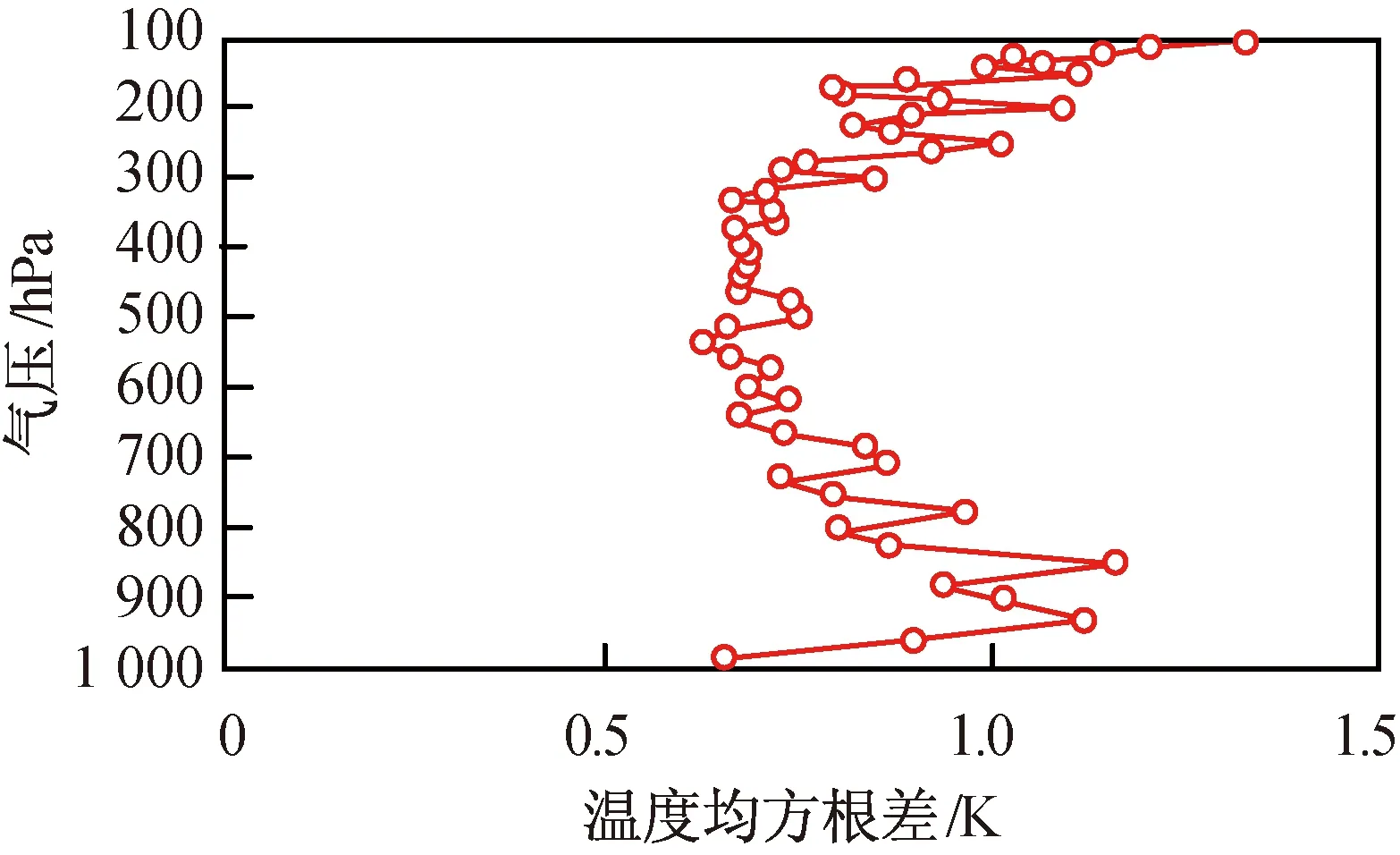
图15 反演对流层温度RMSEFig.15 RMSE distributions of retrieval temperature from stratosphere

3.2.3 平流层(1～100 hPa)大气温度

平流层区域温度反演散点图如图16所示。由图16可知：反演值与样本值有较高的一致性，反演的温度值与样本值的相关系数0.992，均方根误差2.020 K，平均误差0.024 K，反演值与样本值均匀分布在直线y=x两侧。

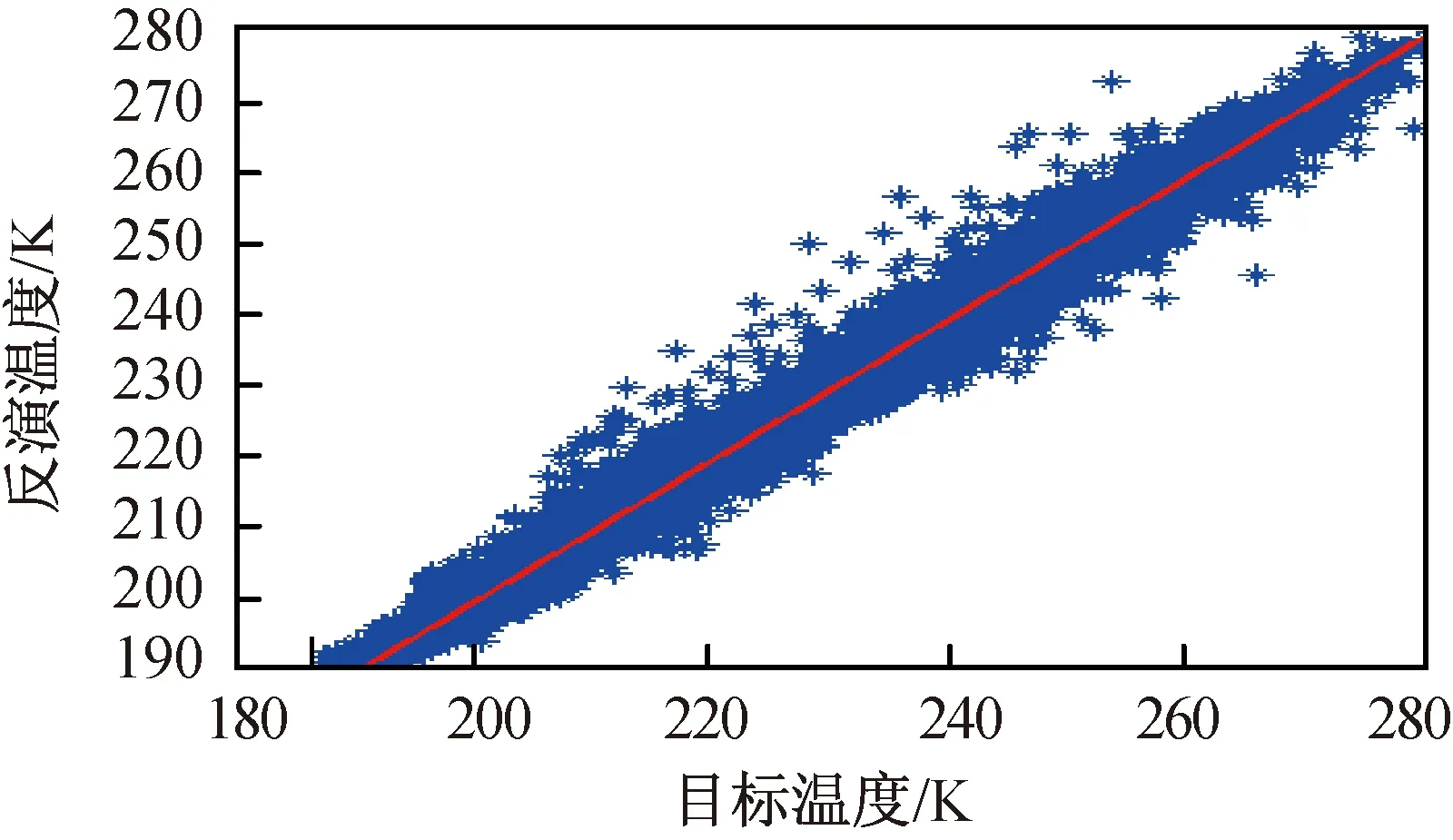
图16 反演温度散点图Fig.16 Temperature scatter diagram of retrieval

反演的平流层温度RMSE如图17所示。由图17可知：平流层区域温度RMSE为2.020 K，最小值1.274 K，平均反演温度的误差范围为-0.233～0.233 K。对流层大气温度反演精度明显高于平流层。

图17 反演平流层温度RMSEFig.17 RMSE distributions of retrieval temperature from stratosphere

GIIRS与欧洲极轨卫星(Metop-A)IASI模拟资料反演大气温度RMSE如图18所示。由图18可知：在气压层区域(1 100～500 hPa)，GIIRS反演温度优于IASI，最优值0.649 K；在高层(<500 hPa)区域，IASI反演大气温度的效果更好，特别在高度1 hPa上，IASI温度反演的RMSE为1.642 K，GIIRS反演温度的RMSE为3.300 K。综合，在低层(>500 hPa)，GIIRS的温度反演精度(RMSE=0.790 K)优于IASI(RMSE=0.976 K)，而在高层(<500 hPa)GIIRS的温度反演精度(RMSE=1.803 K)低于IASI(RMSE=0.899 K)。

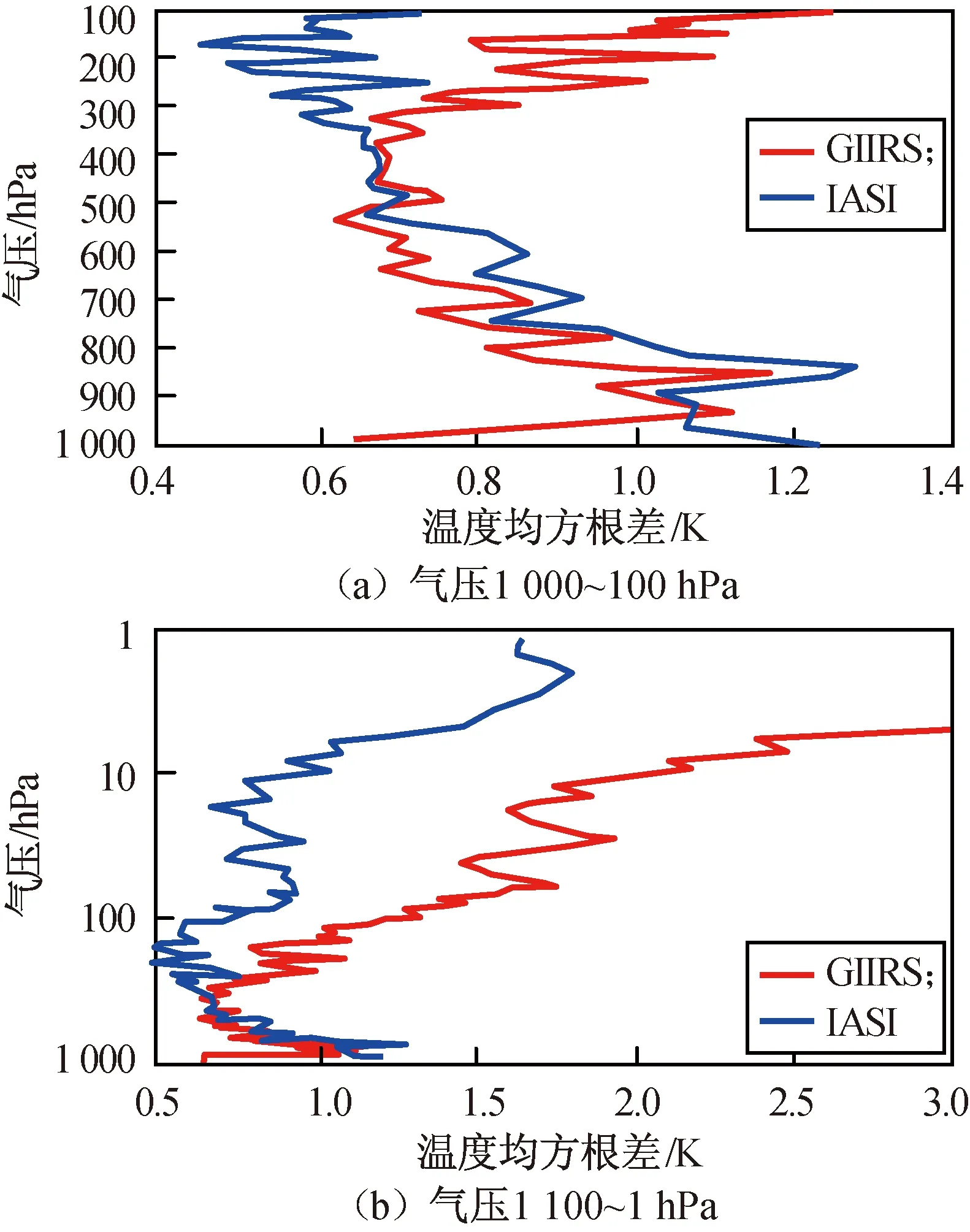
图18 GIIRS，IASI反演大气温度RMSEFig.18 RSME of atmospheric temperature retrieved by GIIRS and IASI

4 结论

FY-4A星是国内第一个装载高光谱红外垂直探测仪的静止轨道卫星，国际上无相关高轨同类载荷的相关研究和反演经验。随着其高光谱红外大气垂直探测仪的处理流程、产品质量等指标的不断完善，在温湿廓线反演研究中使用这些资料的需求将越来越迫切。本文结合全球大气晴空训练样本(CIMSS)数据，用辐射传输模式模拟获得GIIRS亮温资料，用人工神经网络反演方法研究了FY-4卫星高光谱红外载荷大气温度反演方法，并研制了全圆盘和中国区域两套大气温度反演模型。反演试验结果表明：第一，对流层大气温度反演精度明显高于平流层，以中国区域反演模型为例，对流层和平流层大气反演温度RMSE分别为0.846，2.020 K，平均误差分别为-0.003，0.024 K。这主要是因为平流层可用通道数较少。第二，中国区域大气温度误差精度明显高于全圆盘，0～70 km处大气温度反演RMSE分别为1.922，2.630 K。这主要是因为全圆盘区域部分站点的大气温度偏低，而所建模型在较低温度区域的反演误差偏大。第三，FY-4卫星GIIRS的温度反演精度在低层(>500 hPa)优于IASI，在高层(<500 hPa)则低于IASI。

由于FY-4卫星GIIRS在轨实测数据可能存在观测误差和仪器误差，实测值与模拟值间可能存在偏差，这样会增加大气温湿反演误差。为解决此问题，需对实测数据进行订正。后续将基于实测的FY-4卫星GIIRS亮温数据进行大气温度廓线的反演，并对GIIRS温度反演精度在高层误差大于IASI的情况进行更多研究。

致谢：感谢李俊、闵敏和刘辉博士为本研究提供模式，并给予指导。

[1] 董超华, 李俊, 张鹏, 等. 卫星高光谱红外大气遥感原理与应用[M]. 北京: 科学出版社, 2013..

[2] 王颖, 黄勇, 黄思源. 大气温湿廓线反演问题的研究[J]. 国土资源遥感, 2008(1): 23-26.

[3] AIRES F, PRIGENT C, ORLANDI E, et al. Microwave hyperspectral measurements for temperature and humidity atmospheric profiling from satellite: the clear-sky case[J]. Journal of Geophysical Research, 2015, 120(21): 11334-11351.

[4] ISHIMOTO H. OKAMOTO K. OKAMOTO H, et al. One-dimensional variational (1D-Var) retrieval of middle to upper tropospheric humidity using AIRS radiance data[J]. Journal of Geophysical Research: Atmospheres, 2014, 119(12): 7633-7654.

[5] LI J. WOLF W W. MENZEL W P, et al. Global soundings of the atmosphere from ATOVS measurements: the algorithm and validation[J]. Journal of Applied Meteorology, 2000, 39(8): 1248-1268.

[6] 刘天舒. BP神经网络的改进研究及应用[D]. 哈尔滨: 农业工程研究生院, 2011.

[7] 刘旸. 利用人工神经网络方法反演晴空大气湿度廓线的研究[D]. 南京: 南京信息工程大学, 2011.

[8] GANGWAR R K. MATHUR A K. GOHIL B S, et al. Neural network based retrieval of atmospheric temperature profile using AMSU-A observations[J]. International Journal of Atmospheric Sciences, 2014, 10: 1155.

[9] 姚志刚, 陈洪滨. 利用神经网络从118.75 GHz附近通道亮温反演大气温度[J]. 气象科学, 2006, 30(6): 252-259.

[10] 张雪慧, 官莉, 王振会, 等. 利用人工神经网络方法反演大气温度廓线[J]. 气象科学, 2009, 35(11): 137-142.

[11] 刘亚亚, 毛节泰, 刘钧. 地基微波辐射计遥感大气廓线的BP神经网络反演方法研究[J]. 高原气象, 2010, 29(6): 1514-1523.

[12] 蒋德明, 曹思沁, 屈佑铭. 利用神经网络方法从高分辨率红外遥感资料反演大气温度廓线[J]. 热带气象学报, 2010, 26(6): 819-824.

[13] 鲍艳松, 钱程, 闵锦忠, 等. 利用地基微波辐射计资料反演0～10 km大气温湿廓线试验研究[J]. 热带气象学报, 2016, 32(2): 163-171.

[14] 董瑶海. 风云四号气象卫星及其应用展望[J]. 上海航天, 2016, 33(2): 1-8.

[15] 官莉. 卫星红外超光谱资料及其在云检测、晴空订正和大气廓线反演方面的应用[D]. 南京: 南京信息工程大学, 2005.

[16] YANG Y, LIU G. Multivariate time series prediction based on neural networks applied to stock market[C]// IEEE International Conference on Systems, Man, and Cyberneties. [S. l.]: IEEE, 2001: 2680.

[17] 高大启. 有教师的线性基本函数前向神经网络结构研究[J]. 计算机学, 1988, 21(4): 80-86.

[18] DIAMOND C, SHADBOLT J, BARAC M A, et al.Neural network system for tactical asset allocation in the global bonds markets[C]// The 3thInternational Conference Artificial Neural Networks. [S. l.]: [n. l.], 1993: 118-122.

PreliminaryStudyonAtmosphericTemperatureProfilesRetrievalfromGIIRSBasedonFY-4ASatellite

BAO Yan-song1, 2， WANG Zi-jun3， CHEN Qiang3， ZHOU Ai-ming3，DONG Yao-hai4， MIN Jin-zhong1

(1. Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters (IC-FEMD)/Key Laboratory of Meteorological Disaster, Ministry of Education (KLME)/Joint International Research Laboratory of Climate and Environment Change (ILCEC)/Key Laboratory of the China Meteorological Administration Aerosol and Cloud Precipitation, Nanjing University of Information Science & Technology, Nanjing 210044, Jiangsu,China; 2. School of Atmospheric Physics, Nanjing University of Information Science & Technology, Nanjing 210044, Jiangsu, China; 3. Shanghai Institute of Satellite Engineering, Shanghai 201109, China;4. Shanghai Academy of Spaceflight Technology, Shanghai 201009, China)

In this paper, the radiation transfer model was used to calculate the brightness temperature data of Geostationary Infrared Interferometer Sounder (GIIRS) based on the data by the Cooperative Institute for Meteorological Satellite Studies (CIMSS), and the artificial neural network method was applied to build the atmospheric temperature retrieval systems of disc and Chinese regions based on the GIIRS hyperspectral infrared data. The retrieval results show that the atmospheric temperature estimation precision of troposphere is obviously higher than that of stratosphere, the root mean square errors (RMSE) of retrieved atmospheric temperature in the troposphere and stratosphere are 0.846 K and 2.020 K, and the average errors are -0.003 K and 0.024 K respectively. Compared with total disc area, the RMSE of the retrieval model in Chinese region is apparently better, the RMSE of retrieved atmospheric temperature over 0～70 km is 1.922 K, however, the RSME is 2.630 K in the total disc area. Compared with IASI from European polar satellite (Metop-A), the atmospheric temperature estimation precision of FY-4A satellite GIIRS in the lower layers (>500 hPa) (RMSE=0.790 K) is better than IASI (RMSE=0.976 K), but (RMSE=1.803 K) is worse than IASI (RMSE=0.899 K) in high layers (<500 hPa). The study has important value for the retrieval and application of atmosphere temperature profiles from GIIRS based on FY-4A satellite.

FY-4 meteorological satellite; Geostationary Infrared Interferometer Sounder (GIIRS); neural network; temperature profile; retrieval; stratosphere; troposphere; Chinese region; total disc area

1006-1630(2017)04-0028-10

2017-06-08；

：2017-07-28

“六大人才高峰”高层次人才项目资助(2015-JY-013)；国家重点研发计划资助(2016YFA0600703)；上海航天科技创新基金资助(F-201509-0066)

鲍艳松(1976—)，男，教授，博士生导师，主要从事卫星遥感研究。

P423

：ADOI:10.19328/j.cnki.1006-1630.2017.04.004