探究游戏模型中的概率问题
2017-09-14蹇晨雨
蹇晨雨
湖北省沙市中学
探究游戏模型中的概率问题
蹇晨雨
湖北省沙市中学
日常生活中常见的游戏问题大多能以数学思维进行分析,并加以解决。本文通过对常见游戏的研究,分析常见游戏中蕴含的数学模型,并通过概率论的方法对其进行分析讨论,得到常见游戏中普遍的数学规律,旨在解释看起来公平或者选择“理所应当”的游戏是如何存在概率意义上的必然性。
概率;游戏;数学思想;规则制度
一、游戏问题的相关背景
数学,作为多数高中生最为头疼的一门基础学科,大部分人对其持有一种“数学无用论”的看法,认为学数学在生活中用处有限甚至认为学习数学是浪费时间。然而,数学作为基础学科,不仅是学好各大类学科的关键工具,也是解决问题的重要手段。接下来,本文将用数学中的概率论的思维方法解决几个有趣的游戏问题。我们将了解到如何从熟悉的游戏中轻松取胜,并且对其中的原理奥秘用数学思维进行分析,让你在游戏竞争中学会用数学思维分析建模,通过科学的方法做出正确的选择。
二、常见的游戏问题分析
(1)报数问题(报30问题)
游戏背景:甲乙两人轮流报数。从1起,每人每次可报一个数或连续的两个数,谁能报得30谁就获胜。请问:本游戏是否合理,若不合理请说明理由?
分析思考:这是民间流传很久的“抢30”游戏。将问题分析后,可知确认游戏是否合理的关键之处在于先后报数的两人获胜概率是否相同。分析后则将问题转化为求概率问题。
继续对问题进行分析,获胜的关键就在于谁先报到30,根据规则用逆向思维进行分析,谁要想获胜,那他必须报到30或29和30,若他报的数为30,那对方一定报了28、29或28,,那么他只能报27或26、27,继续向下逆推可知,若想获胜一定要报得27、24、21、18……3,故可知,后报数必赢。
因此分类讨论可知:
1.在双方都不知道规则的情况下,任意方先报,则报1或1,2的概率均为1/2,而另一方报2或2,3的概率同样为1/2。故依次推理得知,双方报数时报得27的概率均为1/2。所以最后两人报得30的概率均为1/2。在此条件下,此游戏则为公平的游戏。
2.在双方均知道规则的情况下,若随机选择先后报数,则一方选择后报数则可获得比赛的胜利。在次条件下,比赛则偏向后报数的一方。
3.在一方知道规则条件下,其后报数总能获得胜利。先假设其先报数,则可选择报1或1,2,而对方选择2和2,3的概率则为1/ 2,所以知道规则一方则可选择报3,在其选择报3后对方选择报4和4,5的概率相同,此时知道规则一方必然可以选择5。同理,不知道规则一方报到30的概率为1/2的10次方。
所以,报数问题对于不知道规则的一方完全不公平。
(2)蒙提霍尔问题(三门问题)
游戏背景:假设你参加一个抽奖游戏,主持人在三个小碗下面分别放了1块钱、1块钱和10000块钱的筹码。你选中哪一个,就可以领到对应的钱。当你选定一个碗后,主持人把剩下一个有1块钱的碗翻开,并且,给你一次机会选另外一个碗。请问:应不应该交换?
分析思考:这个问题的结果与常识多少有些相悖,很容易陷入思维误区而错误回答,对这个问题进行分析,应不应该换取决于换不换与最终获奖拿到10000块钱的概率哪个更大。在分析时,我们要知道此类问题隐含着的一个前提:主持人每次打开的碗均为1块钱的碗。则可用如下方法思考:
1.化繁为简,将问题简化为:A.让你先选一个碗,并给你一次机会与余下两个碗交换,换不换?显然,这个结果应该是要换。由于你第一次选择只有1/3的机会选中10000块钱的那个碗,余下两个碗便有2/3的概率选中,所以,交换碗会使选中的概率变大。
B.也就是题目中的情况。主持人将有1块钱的碗翻开,并不会影响整件事情的概率,那另外一个碗依然有2/3的概率是含有10000块钱的,所以,应该与主持人手上的碗交换,因为你选中的概率将从1/3升高为2/3。
2.极限法,将碗的数量增加至10000,则在你选择了1个后,主持人打开剩下的9998个,此时你会不会和剩下的交换。此时,直觉会告诉我们,你不会第一次选就能“万里挑一”,所以会选择交换。即,你第一次选择就能获得10000块的概率为1/10000,此时交换的概率远大于不换的概率。则会选择交换。
3.数学计算,令事件A代表你选择的碗里有10000块,B代表主持人翻开一个里面有1块钱的碗。根据贝叶斯公式:
P(B|A)=1,P(B)=1,则可得到P(A|B)=1/3,所以此时一定要交换。
4.问题拓展,此前我们是在已知主持人的行为,即主持人事先知道碗里的钱数,并且每次打开的均为1元钱的碗,这个前提下来讨论分析问题的。但如果没有给定这个前提条件呢,我们选择交换的概率是否应随着主持人的行为模式发生改变呢?下面我们来看两种情况:
①如果主持人事先并不知道碗里的具体钱数,即翻开碗里的钱数是随机的,服从等概率分布。此时,P(B|A)=1, P(B)=1/3×1+2/3×1/2=2/3,则可得到,这种情况下的P(A|B)=1/2,那么换不换都是一样的概率,并不会影响结果。
②如果主持人还是事先知道碗里的具体钱数,但每次翻开的碗都与你选择的相反,也就是说如果你很幸运的第一次就选中了装有10000元的碗,那么他会翻开剩下两个均装有1元钱的碗其中的一个,仅当你第一次选择的是装有1元钱的碗时,那么他就会翻那只开装有10000元的碗。这种情况下问题就变得很简单,此时的P(B|A)=1,P(B)=1/3×1+2/3×0=1/3,可求出P(A|B)=1,很显然这时你是绝对不能换的。
(3)循环连胜问题
游戏背景:甲、乙、丙三人进行比赛,规定甲与乙先比一盘,胜者与丙比,依次循环,直到有一人连胜两盘为止,此人即为冠军。假定每盘比赛双方取胜的概率均为1/2,问这个比赛规则合理吗?
分析思考:此题有关赛制类问题,我们可以假设若甲最终取得胜利,来求他获胜的概率。设事件A为甲最终赢,事件D为甲赢了第一局,则由全概率公式可知:P(A)=P(A|D)×P(D)+P(A|Dˉ)×P(Dˉ),设P(A|D)=a,P(A|Dˉ)=b,且甲在第一局赢了的条件下,最终赢了的事件也包括第二局输或赢,所以如果第二局输了,情况可以等效于第一局输了,最后获胜;同理,在第一局输了的条件下,第二局只能获胜,但第三局又可以输或赢,这情况又等效于第一局赢了,最后获胜。故可得:a=1/2+1/2b b=1/2×1/2a,解得:a=4/7 b=1/7,所以由全概率公式可以计算出P(A)=5/14,同理乙最终获胜的概率和甲相同,也为5/14,丙获胜的概率为1-5/14-5/14=4/14,也就是2/7,显然,三人获胜的概率不同,从中,也可以发现,先进行比赛的人,获胜的概率较大,所以规则并不合理。
三、游戏中蕴含的思想与启示
(1)游戏在我们生活中普遍存在,掌握它其中的概率问题,也就相当于掌握了制胜的法宝,使我们获胜的概率增大许多。
例如很多体育竞技项目,在赛事前选手的出场顺序、比赛场地、竞技对手等都是由抽签这一环节来决定的,通常都会选择抛硬币的方式,鉴于这种方法简单易得同时又满足公开公平的原则,但有些重大的赛事前的抽签环节,为了防止出现作弊等任何纰漏达到更严谨的状态,有时也是考虑到起到营造整个比赛的紧张氛围,则会采取一些更为复杂、新颖的抽签方式。
例如1999年足协杯在最后总决赛的主客场次序抽签环节就不仅是抛硬币那么简单,其选择的方式为:先分别由两队选择单数还是双数,然后再分别由两队从数字1到9之间任意抽选一个数字,并求和,如若求和结果为单数,则由选择单数的球队选择主客场次序,反之则由选择双数的球队来决定。但这其中选择单、双的结果是不是完全一样的呢,得到的结果又是否真的做到完全的公平呢,让我们把它抽象为数学的概率问题来探究这个方式是否真的合理可行。
1.抽象问题:从数字1到9之间任选两数并做求和运算,其结果为奇数还是偶数的概率是否相等?
2.概率分析:不妨设A:“选出的数字求和结果为偶”,B:“选出的两个数字都为偶”,C:“选出的两个数字都为奇”。显然A=
3.结果分析:通过数学概率的计算,我们可以得出结论,在这个抽签环节中,选择单数的球队获得主客场次序选择权的机会更大一些,有55.5%的机会。显然这个抽签方式的制定存在一定的漏洞,并不能做到完全的公平,如果在事先了解它其中的概率问题,那么就能充分利用这一规则上的疏忽,在比赛中抢先占据有利地位。这同时又在另一方面提醒比赛规则的制定者,在制定并赛规则时应更加严谨,尽量保持比赛的合理性、公平性。
例如A、B两个人做一道判断对错的问题,答案无非两种,非对即错,显然两人的正确率并无并无什么区别都是1/2,假设在两进一步考虑,如果是A、B、C三个人一起做同一道多选题呢,当其中两人的选择结果相同时,他们选择正确的概率是多少?选择的人越多是否就代表着这就是正确答案呢?这里我们假设每个人选择的正确率均为p,同时剩余n个错误选项每个出现的概率也相同均为q,p+nq=1。此时选择相同的两人选择正确的概率为。同时这个概率又要满足大于一个人的正确率p,即我们可以得出结论,在p>q,即正确选项的概率要大于其余每个错误选项的概率的前提下,选择的人越多那么就代表着这个选项就是正确的答案。
(2)研究此类问题,其中蕴含了许多数学思想,例如逆推思想、化繁为简思想、分类讨论思想等等,这更加体现出了数学的广泛应用以及它在生活中发挥的巨大作用。同时,这也像我们展示了,数学思想的灵活运用,以及一些基本的概率公式。
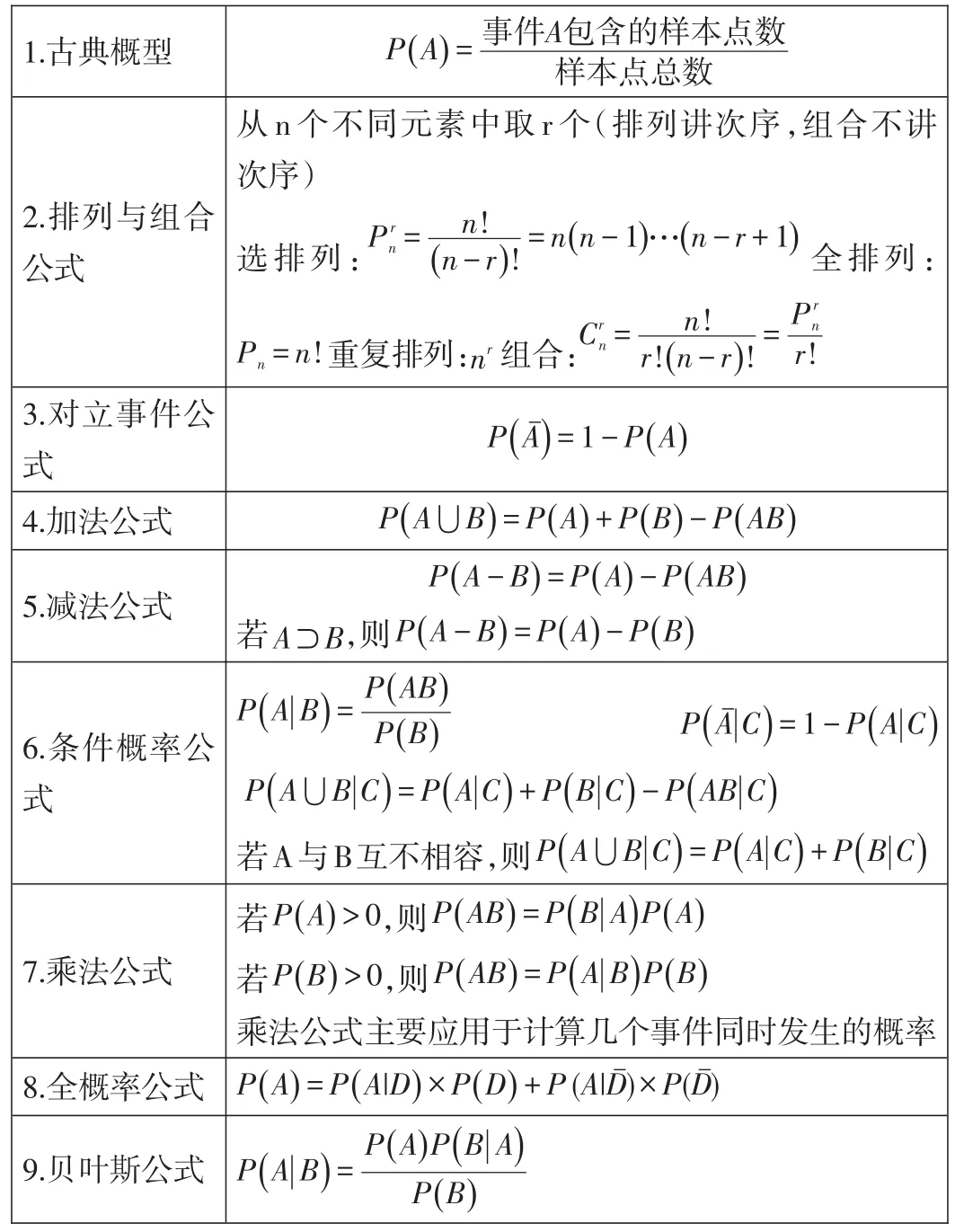
1.古典概型P()事件A包含的样本点数样本点总数从n个不同元素中取r个(排列讲次序,组合不讲次序)选排列:Pr2.排列与组合公式n= A= n! () n-r!=n() n-1…() n-r+1全排列:Pn=n!重复排列:nr组合:CrPrn n! r!() A+P()n=n-r!= Aˉ=1-P() A 3.对立事件公式4.加法公式5.减法公式P() r! P() A⋃B=P()B-P() AB若A⊃B,则P() A-B=P() A-P() AB P() A-B=P() A-P() B P() 6.条件概率公式A|B=P() P() Aˉ|C=1-P() A|C AB P() B AB|C若A与B互不相容,则P() A⋃B|C=P() P()A|C+P() B|C-P() A|C+P() B|C若P() A⋃B|C=P() A>0,则P() AB=P() B|A P() A 7.乘法公式若P() B>0,则P() AB=P() 8.全概率公式9.贝叶斯公式A|B P() B乘法公式主要应用于计算几个事件同时发生的概率P() A=P() A|D×P() D+P(A|Dˉ)×P(Dˉ) P() A|B=P() A P() B|A P() B
[1]王儒智.游戏规则中的概率问题[J].昌潍师专学报,2000,4(2),69~70.
[2]唐国兴.高等数学(二)第二分册[M].武汉:武汉大学出版社,1991.
[3]经家麒.抢数游戏及其推广[J].数学通报,1992(2).
[4]潇寒.[EB/OL].https://www.zhihu.com/question/37861500/an⁃swer/79406813.
