例谈数形结合思想在数学教学中的应用形式
2017-09-13陈玉玲
陈玉玲

【摘要】本文从“以形表数,以形想数,以形助数,以形解数”等方面展开论述,借助数形结合思想把复杂问题具体化,把抽象问题形象化,拓宽学生的思路,提高学生的解题能力,促使学生达到深刻理解所学知识的目的。
【关键词】小学数学 课堂教学 数形结合思想
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2017)07A-0071-02
数形结合思想是数学新课标的核心理念,鉴于“数”和“形”是贯穿整个小学数学教材的两条主线,“数”构成了数学的抽象化符号语言,“形”构成了数学的直观化图形语言的特点。在小学数学课堂教学中,借助数形结合思想可以有效地降低学生的学习难度,进而使学生的数学学习显得更加轻松、有效。那么,数形结合思想在小学数学课堂中如何应用才能更为合理、有效呢?笔者认为,教师可以从以下四个方面入手。
一、以形表数
抽象概括是概念的本质特点,在概念教学中,由于学生大多是以形象思维占主导,因而在理解概念方面具有一定的难度。针对这种现状,教师如能根据概念的特点,运用数形结合思想,则可以进一步帮助学生建立抽象概念与形象直观之间的桥梁,进而使学生能够达到轻松理解数学概念的目的。
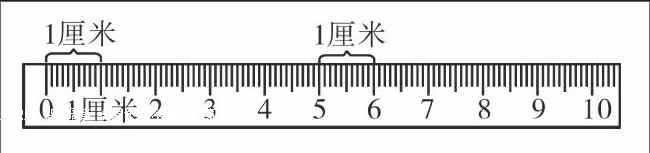
如在教学人教版数学二年级上册《厘米和米的认识》这部分知识时,教师不能单从1分米=10厘米,或者教师的口头讲述来让学生理解,而应根据学生容易被直观具体的事物所吸引的特点,采用数形结合的方法加深学生的理解,在学生对厘米和米这种长度单位有了大致认识的基础上,教师再通过多媒体技术向学生展示下图。
在这直观的图示中,借助图上的标注,学生明白了1厘米指的并不是0到1刻度的距离,而是任意两个相邻刻度之间的距离是1厘米,在这种情形下,以形表数,学生对厘米这个概念的认识更加深刻,起到了良好的教学效果。
在上述教学案例中,在“厘米”这个概念的认识上,为了使学生的感受更深刻,并且让学生对厘米的认识不再机械片面,教师主要借助了数形结合思想来深化学生的思想认识,进而拓宽了学生的思维面。
二、以形想数
在数学教学中,鉴于数学所学知识之间的逻辑性、抽象性比较强的缘故,教师可以采取数形结合的形式帮助学生找到解决数学问题的支撑点,进而让学生对数学知识有更好的了解与认识,从而促进学生对所学知识的理解与认识,提高教学效果。
如在教学《植树问题》时,由于学生本身生活经验不足,也缺乏植树的生活经历,因而在面对“两端种树”“一端种树”“两端都不种”“棵树”“间隔”等具体问题时,单凭学生的想象很难获得对所学知识的深刻理解。因此,为了帮助学生更好地理解所学知识,降低学习难度,教师主要采取了数形结合的方法来帮助学生理解。于是,借助多媒体,教师向学生展示了下图:
这样一来,在直观图例的示范下,学生可以清楚地看到什么是间隔,什么是段数以及关于栽种的具体情况,并对这些概念有了全方面的了解与认识,有助于学生获得对植树问题的真正认知,学习效果显著。
在上述案例中,针对学生对植树问题中的相关知识了解较浅等现象,教师主要借助多媒体和数形结合的思想,向学生全面展示了植树问题中可能出现的各种情况,进而让学生对所学知识的认识更加深刻,起到了显著的教学效果。
三、以形助数
计算教学作为数学学习内容的重要组成部分,教学时,在一些算理算法的理解上,由于一些理论知识比较抽象,教师可以借助数形结合思想,帮助学生把抽象难懂的计算过程变得直观、具体,如此一来,就能够比较容易帮助学生建立起数学知识之间的一一对应关系,有效降低学习难度,深化学生对所学知识的理解。
如在教学《有余数的除法》这部分内容时,由于学生已经具备了学习除法的初步经验,掌握了基本的操作要领。但是,在实际教学中,学生对有余数除法中“余数一定要比除数小”这个理论还缺乏足够的认识,为了帮助学生更好地理解这个算理,教师让学生拿出小棒,分别摆出:10÷9=、10÷8=、10÷7=、10÷6=……10÷3=……这些算式的结果。在此基础上,再让学生仔细观察这些算式中每个算式的商是多少?余数是多少?余数与商之间有什么关系?如果出现余数大于除数,这种现象说明了什么?这样教学,在直观的小棒的展示下,學生真正明白了余数比除数小的原因,收到了良好的教学效果。
在上述案例中,在关于“有余数的除法”的教学上,为了使学生真正明白其中隐含的算法算理的本质特点,教师主要采取了借助数形结合思想来帮助学生突破学习难点的教学方法,有效地化抽象为具体、化抽象为简单,促使学生轻松地获得对所学知识的深刻感受,教学效果显著。
四、以形解数
在小学数学教学中,有一些数学问题比较抽象,而且数量关系也比较隐秘,学生在解决问题的过程中不容易发现,或被运用到学习中。画图作为一种常用的解题方式,教师如能根据习题的特点,通过画图的形式帮助学生把习题中的隐秘条件一一发现并发掘出来,从而帮助学生找到解题的有效策略,将学生的思维真正引向深处。
如在教学“一块长方形的试验田,如果这块田地的宽增加4米,或者长增加6米,这块长方形试验田的面积都会比原来增加48平方米,求原来长方形试验田的长与宽各是多少?”这道习题由于已知条件比较复杂或者模糊,学生在解决问题时常常会有一种无从下手的感觉,为了降低学习难度,笔者主要采取了数形结合的方法来帮助学生理解。于是,根据习题信息,教师把文字信息转化成了下面的图形信息:
在直观图示的提示下,学生通过观察发现,如果用48÷4就可以得出长方形的长是多少,用48÷6就能得出长方形的宽是多少。如此教学,可以使学生不仅知其然而且知其所以然,真正使学生的数学学习走向深刻。
在上述案例中,由于习题中的条件较为复杂,学生理解接受起来具有一定的难度,针对这个特点,教师采取了借助数形结合思想来帮助学生理解习题的教学方法,有效地降低了学习难度,起到了良好的教学效果。
综上所述,数形结合思想在小学数学课堂应用的领域是非常广泛的,教师只有根据所学知识的特点,找准数形结合思想的着力点,并注重在课堂中的渗透与运用,那么,就可以真正达到为提高学生数学学习质量的目的。
(责编 林 剑)endprint
