几类Kantorovich型插值算子在Orlicz空间内的逼近
2017-09-12高雅吴嘎日迪
高雅,吴嘎日迪
(内蒙古师范大学数学科学学院,内蒙古 呼和浩特 010022)
几类Kantorovich型插值算子在Orlicz空间内的逼近
高雅,吴嘎日迪
(内蒙古师范大学数学科学学院,内蒙古 呼和浩特 010022)
分别讨论了以第二类Chebyshev多项式的零点、Jacobi多项式的零点、第一类Chebyshev多项式的零点为插值结点组的五类Kantorovich型插值算子在Orlicz空间内的逼近问题,得到了逼近阶的上界估计.
Kantorovich插值算子;Orlicz空间;Chebyshev多项式;Jacobi多项式;逼近
1 引言和主要结果

x=cosθ是n次第二类Chebyshev多项式.
在文献[1]中,∀f∈C[-1,1],以第二类Chebyshev多项式的零点为插值结点组的f的Bernstein型插值算子定义为:
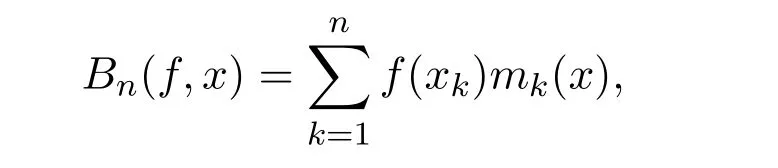
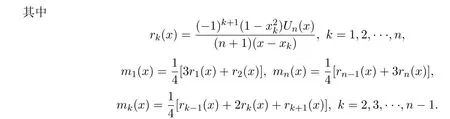
在文献 [2]中,以第二类 Chebyshev多项式的零点为结点构造了一个
组合平均的Bernstein型插值多项式算子,具体形式如下:
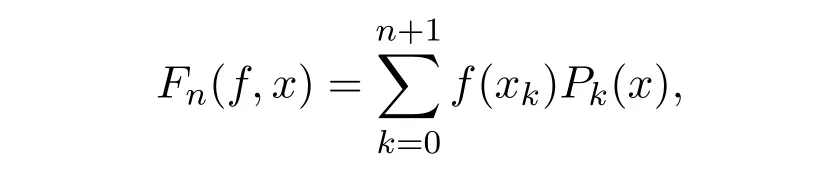
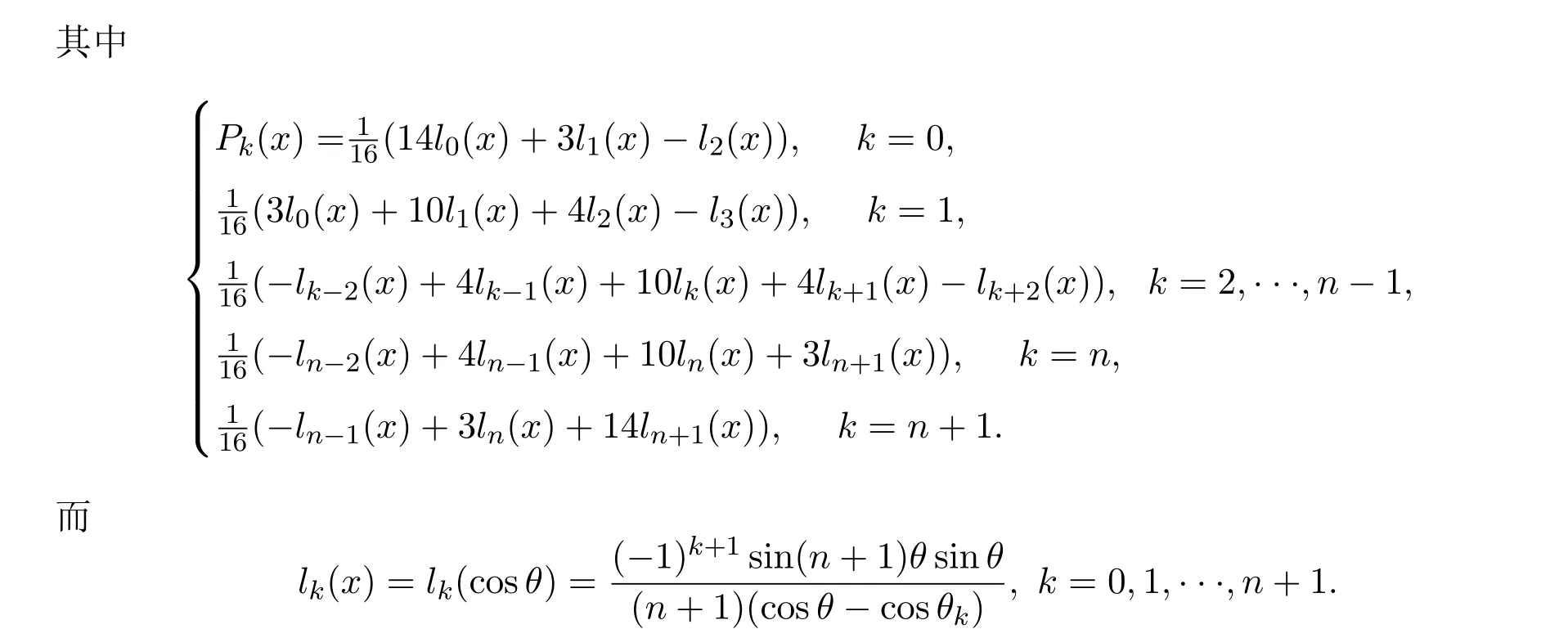
在文献[3]中,定义了另一类以第二类Chebyshev多项式的零点为结点的Bernstein型插值算子Gn(f,x),其定义如下:


设 f∈C[-1,1],xk是第一类Chebyshev多项式Tn(x)=cosnθ,x=cosθ,0≤θ≤π的零点.

文献[5]以Tn(x)的零点作为插值结点定义了一个Bernstein型插值多项式,定义如下:

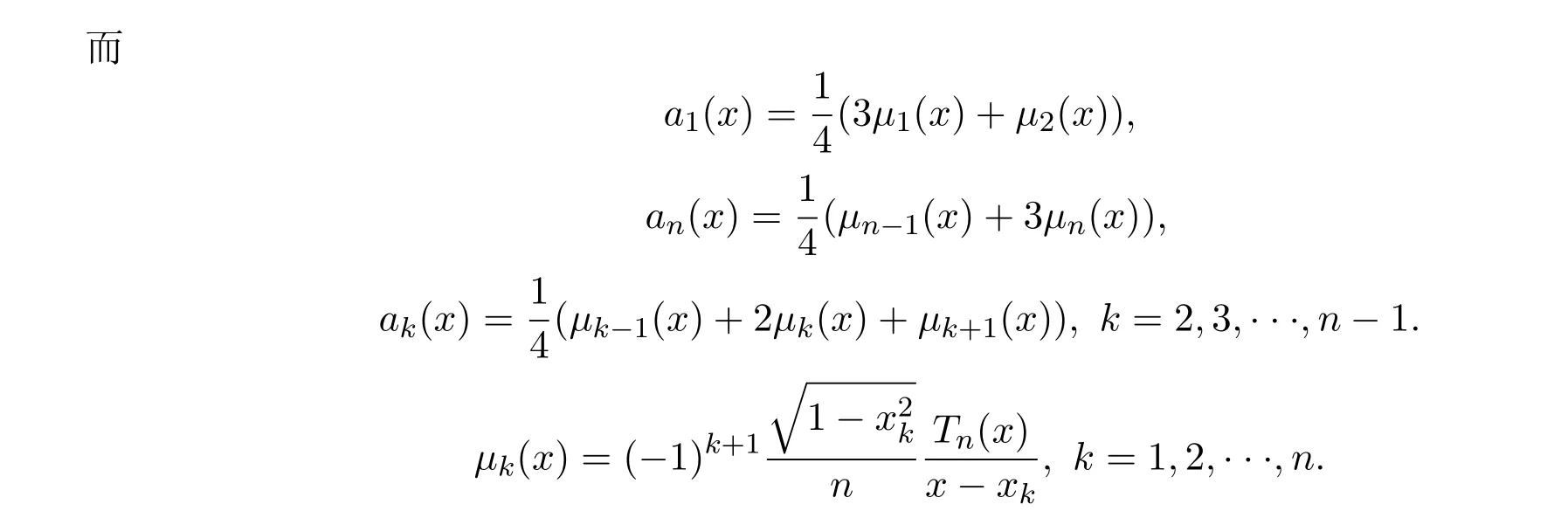
本文首先将以上五个Bernstein型插值算子修正为Kantorovich型插值算子,即
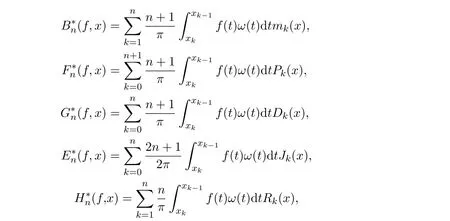
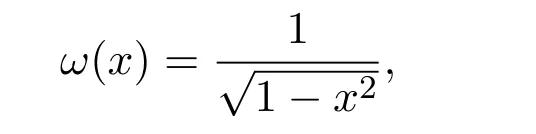
进而研究这五个修正后的插值算子在Orlicz空间内的逼近性质.
本文用M(u)和N(v)表示互余的N函数,关于N函数的定义及性质见文献[6].由N函数M(u)生成的Orlicz空间是指具有有限的Orlicz范数
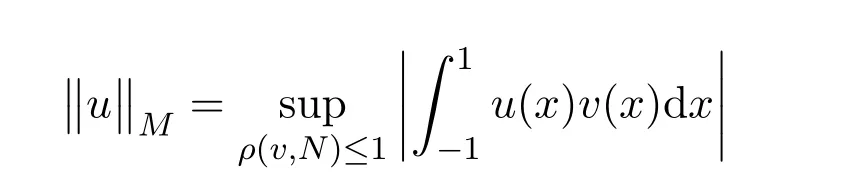
的可测函数{u(x)}全体,其中
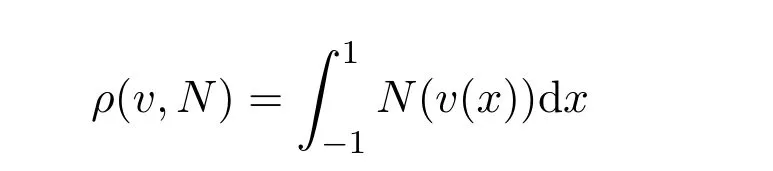
是v(x)关于N(u)的模.由文献[6]知上述Orlicz范数还可以由
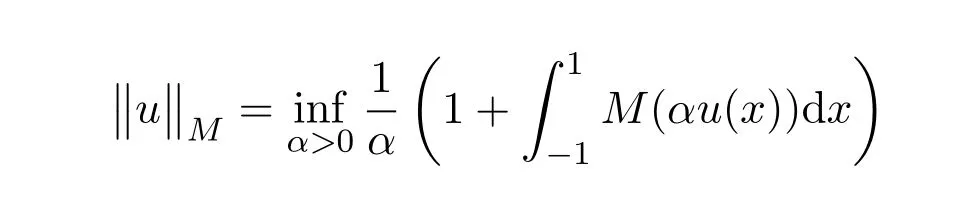
来计算.

其中
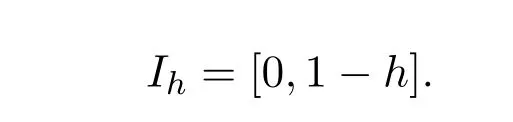
本文的主要结果:
定理 1.1若,则存在常数 C >0使得
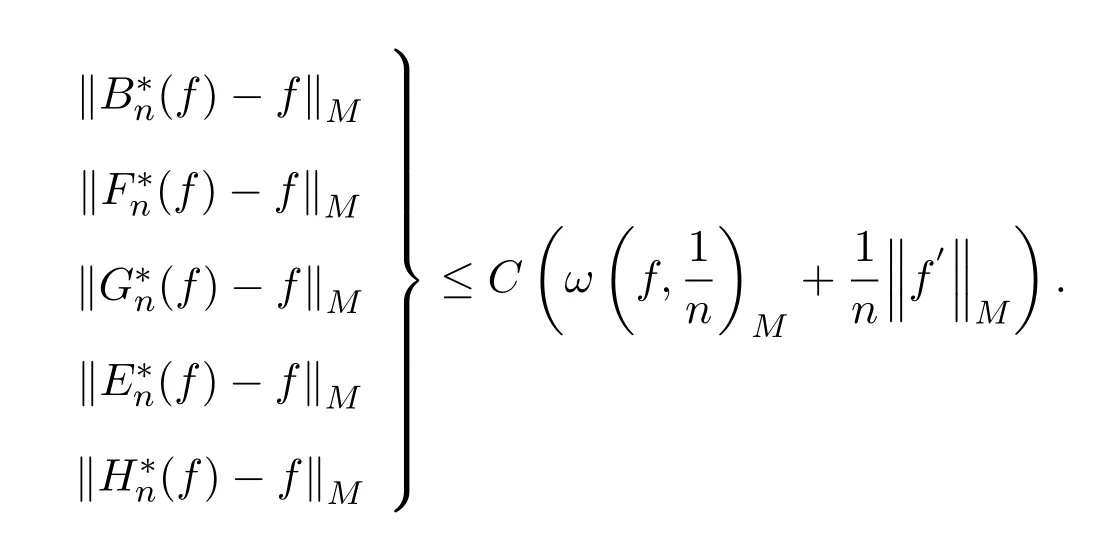
注 1.1用C表示与n无关的正常数,在不同处可以表示不同的值.
2 若干引理
引理 2.1[6](Holder不等式) 对任意 u(x)∈L∗M,v(x)∈L∗N,有
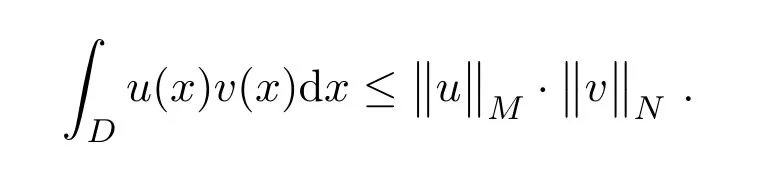
引理 2.2[7],则
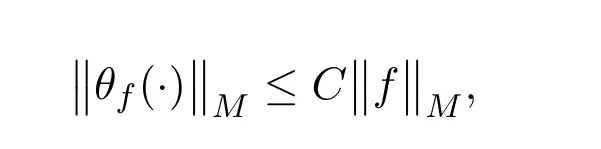
其中
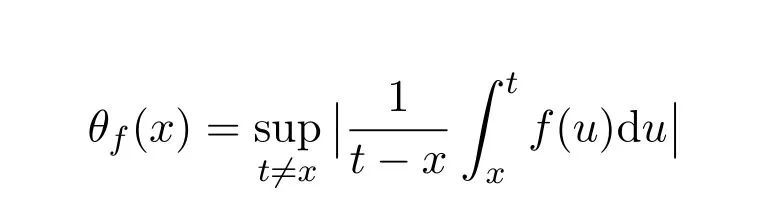
是f的极大函数.
引理 2.3对任意正整数n,
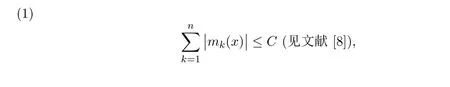

引理 2.4[11]对任意,存在n次代数多项式Pn(x),使得
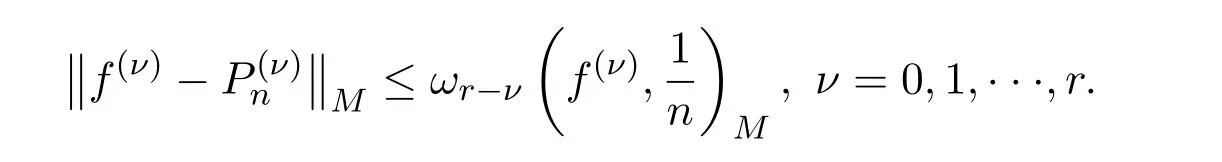
3 定理的证明

利用引理2.1得,上式中的

由引理 2.1 和
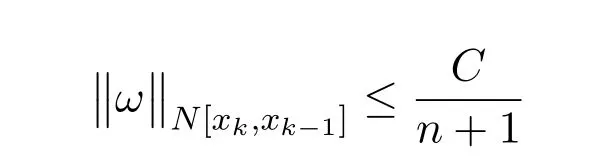
以及u(t)、v(t)在 [xk,xk−1]上的本性有界性知,
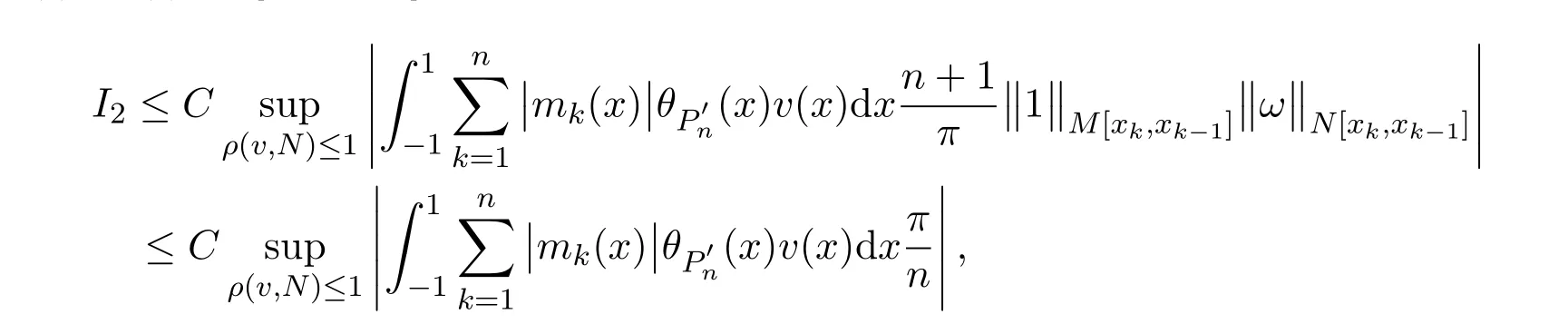
再由引理2.1、引理2.2、引理2.3以及v(x)在[-1,1]上的本性有界性,得



参考文献
[1]Varma A K.On an interpolation process of S.N.Bernstein[J].Acta Math Acad Sci Hungar,1974,31:57-62.
[2]崔利宏,金明爱,盛国辉.关于一个Bernstein型插值多项式的点态估计[J].延边大学学报,1997,23(4):10-14.
[3]Chauhan B P S,Srivastava K B.Uniform convergence and rapidity of convergence of Grunwald-type operators on extended Chebychev nodes of second kind[J].Indian.J.pure appl.,1978,9:1337-1343.
[4]Kis O.Certain interpolation processes of S.N.Bernstein[J].Acta Math.Acad.,Sci:hungar,1973,3:353-361.
[5]王淑云,何甲兴,成丽波.Bernstein算子和Grunwald算子的线性组合[J].吉林大学学报,2005,43(1):5-9.
[6]吴丛炘,王廷铺.奥尔里奇空间及其应用[M].哈尔滨:黑龙江科学技术出版社,1983.
[8]谢庭藩,孙燮华.关于Bernstein型和Bernstein-Grunwald型插值过程[J].数学学报,1985,28(4):455-469.
[9]孙燮华.两个Bernstein型插值过程的逼近阶[J].数学年刊,1984,5A(3):347-354.
[10]王淑云,孙毅,何甲兴.关于一个 Bernstein型插值过程收敛阶的点态估计 [J].吉林工业大学自然科学学报,2001,31(1):43-46.
[11]Wu Garidi.On approximation by polynomials in Orlicz spaces[J].Approximation Theory and its Applications,1991,7(3):97-110.
Approximation of several Kantorovich interpolation operators in Orlicz space
Gao Ya,Wu Garidi
(College of Mathematics Science,Inner Mongolia Normal University,Hohhot 010022,China)
In this paper,we study the approximation properties of fi ve kinds of Kantorovich interpolation operators in Orlicz space based on the zeros of the Chebyshev polynomials of the second kind and the Jocabi polynomials and the Chebyshev polynomials of the fi rst kind,we obtain the upper bound of estimation of approximation.
Kantorovich interpolation operator,Orlicz space,Chebyshev polynomial,Jacobi polynomial,approximation
O174.41
A
1008-5513(2017)04-0359-11
10.3969/j.issn.1008-5513.2017.04.004
2017-05-19.
国家自然科学基金(11161033);内蒙古自治区研究生科研创新基金(S20161013501);内蒙古自治区自然科学基金(2017MS0123).
高雅(1993-),硕士生,研究方向:函数逼近论.
2010 MSC:40A05
