基于PI控制器的不确定广义系统的非脆弱耗散控制
2017-09-12黎虹
黎虹
(沈阳工学院基础课部,辽宁 抚顺 113122)
基于PI控制器的不确定广义系统的非脆弱耗散控制
黎虹
(沈阳工学院基础课部,辽宁 抚顺 113122)
主要研究了一类不确定广义系统的耗散控制问题,基于线性矩阵不等式的处理方法给出了使广义系统容许且严格耗散的充要条件,并利用线性矩阵不等式的解给出了耗散控制器的设计方法,得到了一个具有非脆弱性的状态反馈PI控制器的显示表达,使得对所允许的不确定性闭环广义系统容许且严格耗散.最后用数值例子说明了所提出方法的正确性和有效性.
广义系统;严格耗散;PI控制器;非脆弱控制
1 引言
近几年,耗散性的概念逐渐被推广到广义系统中,并取得了一些好的研究成果[18].文献[1-5]利用线性矩阵不等式的方法,在适当假设下,分别给出了线性连续广义系统、滞后离散广义系统容许且严格耗散的充分必要条件,并且分别给出了状态反馈、动态输出反馈及基于观测器的严格耗散控制器的存在条件和设计方法.文献[6]研究了广义离散系统的鲁棒脉冲耗散控制问题.文献[7-8]研究了广义离散切换系统的耗散控制问题.随着信息技术的迅速发展,很多新型控制器不断涌现,但PID控制器由于其结构简单、鲁棒性能好并且易于操作等优点,仍然是目前使用最广泛的一种控制器,在各类系统中得到广泛的应用.运用耗散性理论,可以充分运用反馈控制器的增益和相位信息,使所得结果具有较小的保守性[9].基于这一理论,文献[10]考虑了基于PI控制器的正常线性系统的鲁棒耗散控制问题.
目前,关于PID控制器在广义系统中的耗散控制问题中的运用还未见报道.本文设计了状态反馈PI控制器,使闭环广义系统容许且鲁棒严格耗散,最后采用文献[10]中数值例子,计算得到了小增益控制器,具有更小的保守性.
2 问题描述
考虑如下的广义系统:
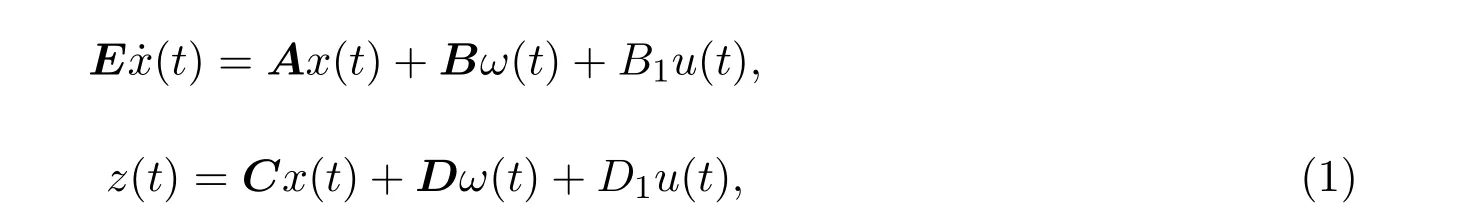
其中,x(t)∈Rn为系统状态,ω(t)∈Rq为外部扰动输入且满足:
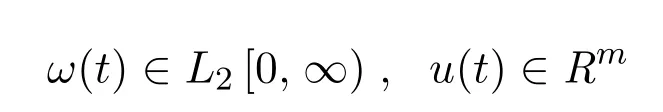
为控制输入,z(t)∈Rr为输出,矩阵E∈Rn×n为奇异矩阵,且系统中的其它矩阵为已知的具有适当维数的实常数矩阵.
针对系统(1),选择如下能量供给函数:
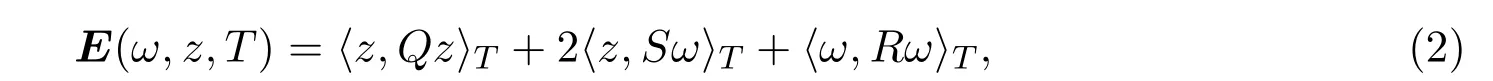
其中,Q,R为给定的对称矩阵且具有适当维数,S为给定的具有适当维数的矩阵,且
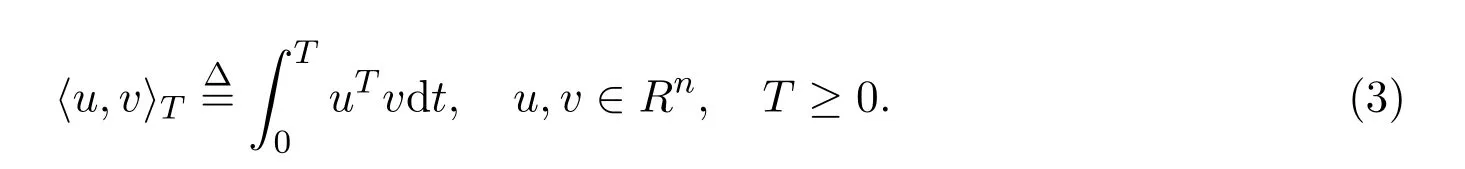
定义 2.1[1]对于能量供给函数(2),若

成立,则称系统(1)(u=0)是(Q,R,S)-耗散的.且如果对于T>0和足够小的α>0,有

成立,则称系统(1)是严格(Q,R,S)-耗散的.
假设2.1

引理 2.1[1]对于给定的矩阵Q,R,S和系统(1)(u=0),以下命题是等价的:
1.系统(1)容许且严格(Q,R,S)-耗散的;
2.存在矩阵P 可逆,使得


3 基于 PI控制器的严格耗散控制
设计如下状态反馈的PI控制器:
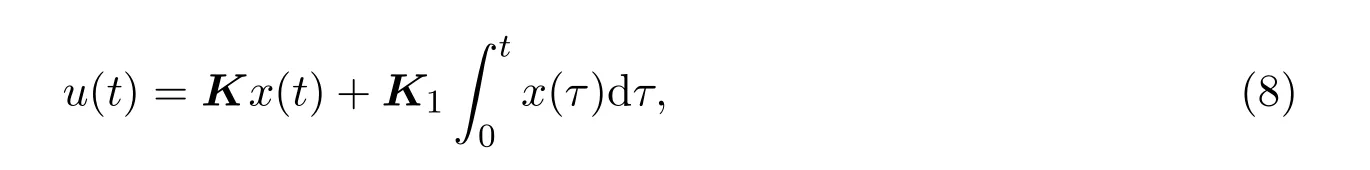
其中K,K1为待定的参数矩阵,使闭环广义系统

容许且严格(Q,R,S)-耗散,且有
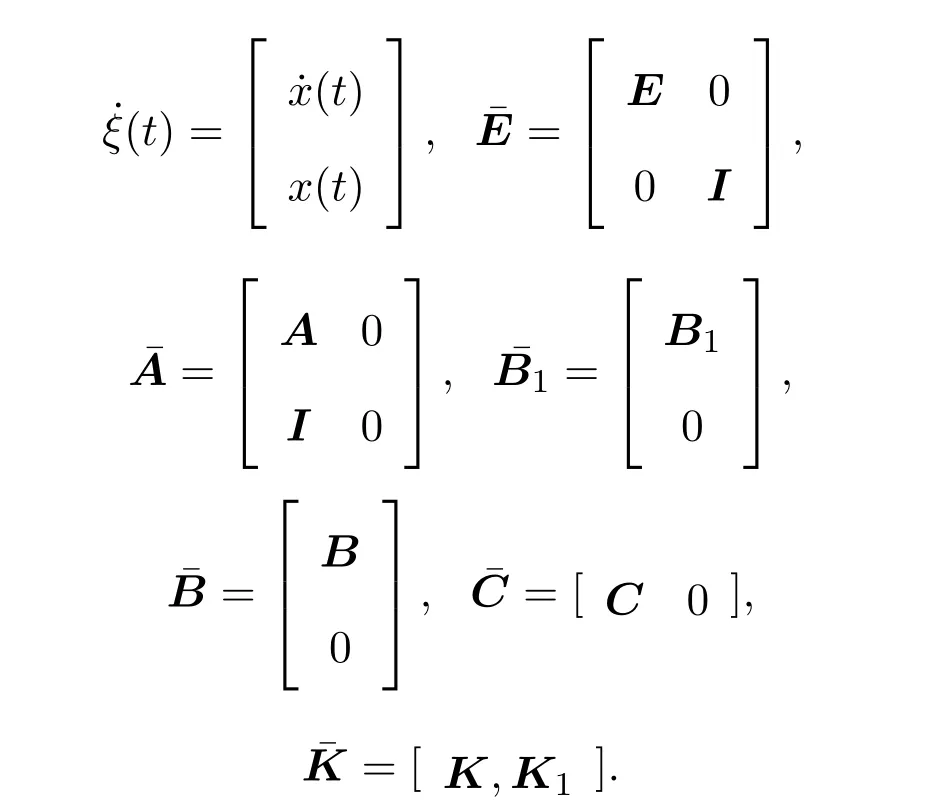
由引理2.1即可得到状态反馈PI控制器的存在条件和设计方法.
定理 3.1矩阵Q,R,S为给定矩阵且满足假设2.1,对于闭环系统(9),存在一个状态反馈PI控制器,使其严格(Q,R,S)-耗散的充分必要条件是:存在可逆矩阵Y 和W 使得不等式(10),(11)式成立.

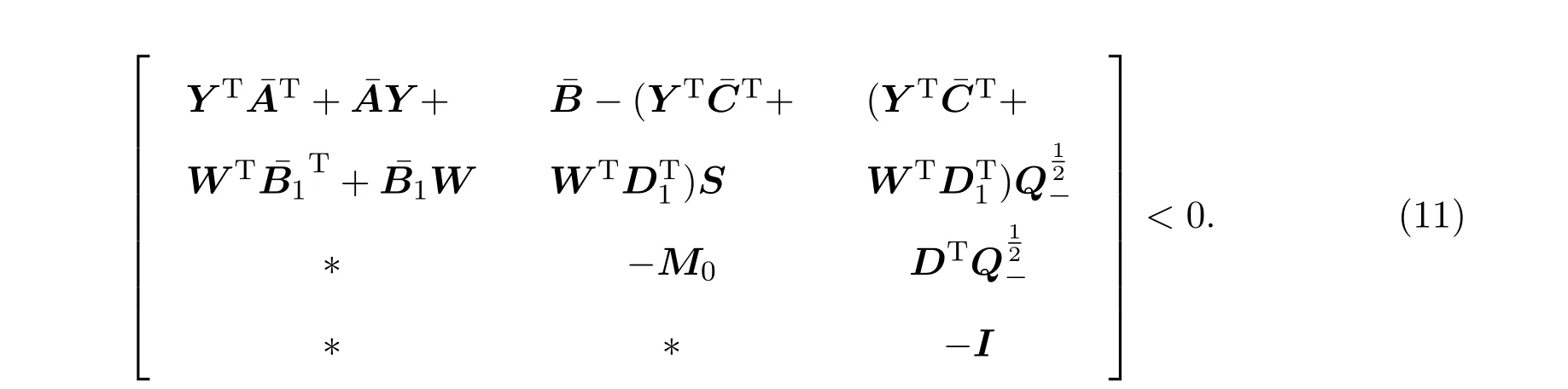
如果矩阵不等式(9),(10)存在一个可行解Y 和W,则

为一个状态反馈的耗散控制器,PI控制器增益的显示表达式由
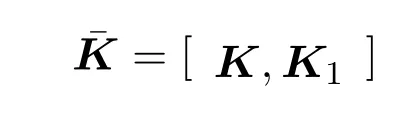
得到.
证明将增广系统(9)代入引理1得到
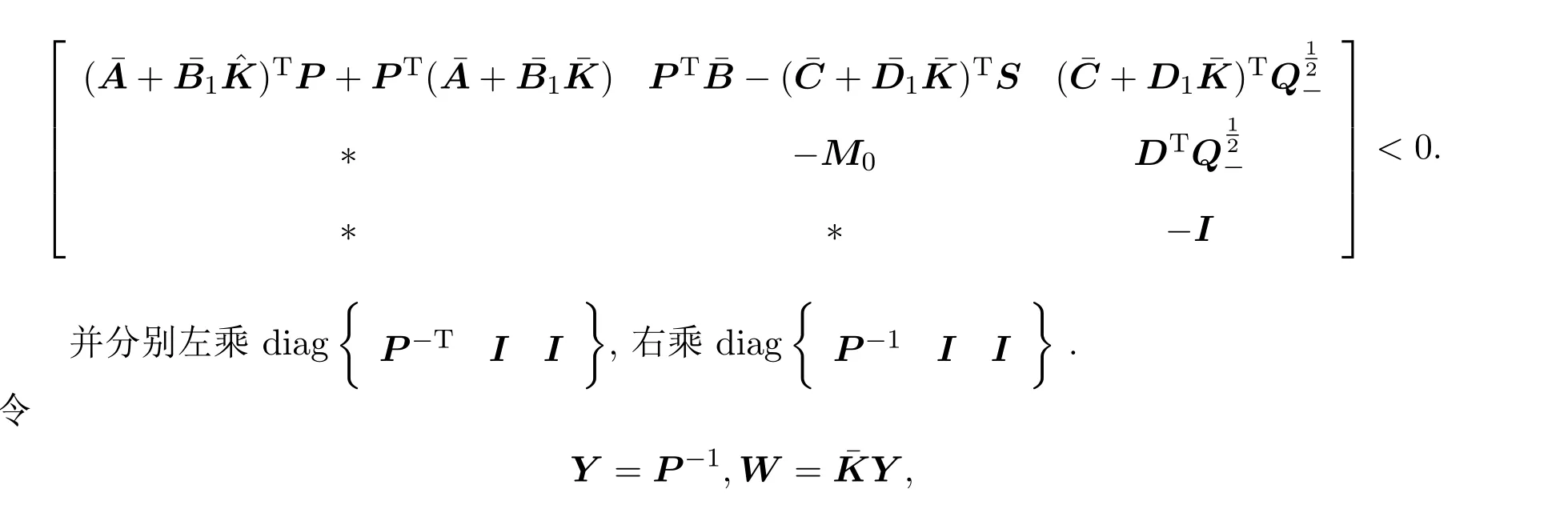
即可得证.
4 基于非脆弱 PI控制器的鲁棒严格耗散控制
考虑如下的不确定系统:

其中,参数不确定矩阵满足

且有
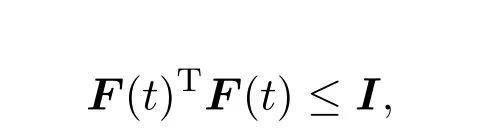
H1,H2,E1,E2,为已知矩阵.
引理 4.1[11]矩阵Q,R,S为给定且满足假设1,对于系统(12)(u=0),使其严格耗散的充分必要条件为:存在常数ε>0和矩阵P可逆,使得矩阵不等式(13),不等式(14)成立

考虑系统(12),设计非脆弱PI控制器:
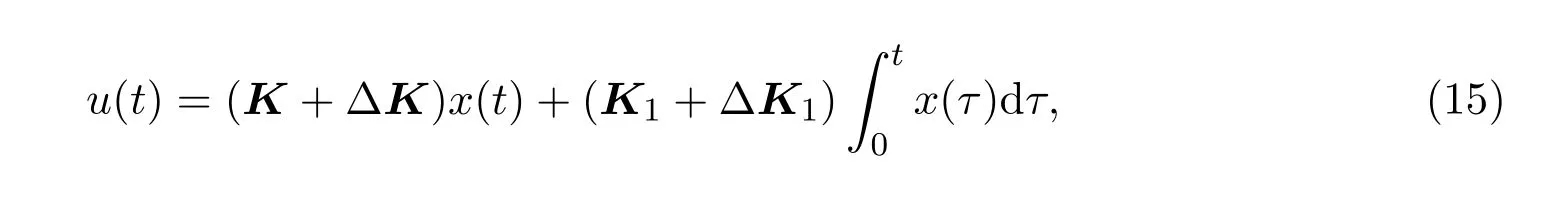
其中

E3为已知矩阵.
将非脆弱PI控制器(15)代入系统(12)可得闭环广义系统

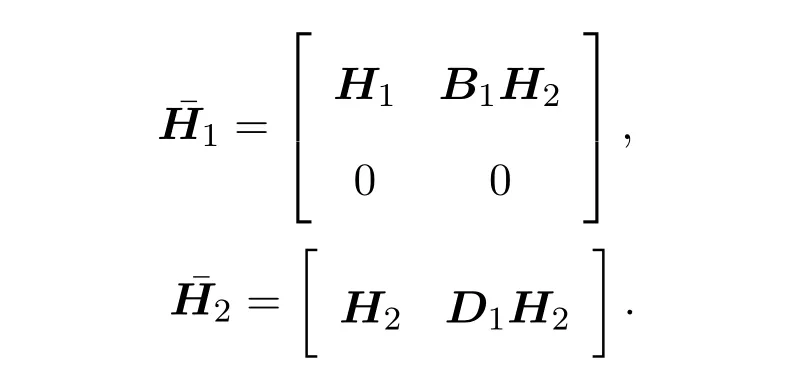
运用引理4.1,可以得到如下定理4.1.
定理 4.1给定矩阵Q,R,S满足假设2.1,对于闭环广义系统(16),存在一个状态反馈的非脆弱PI控制器,使其(Q,R,S)-耗散的充分必要条件是:存在常数ζ>0,可逆矩阵Y和W 满足如下不等式:

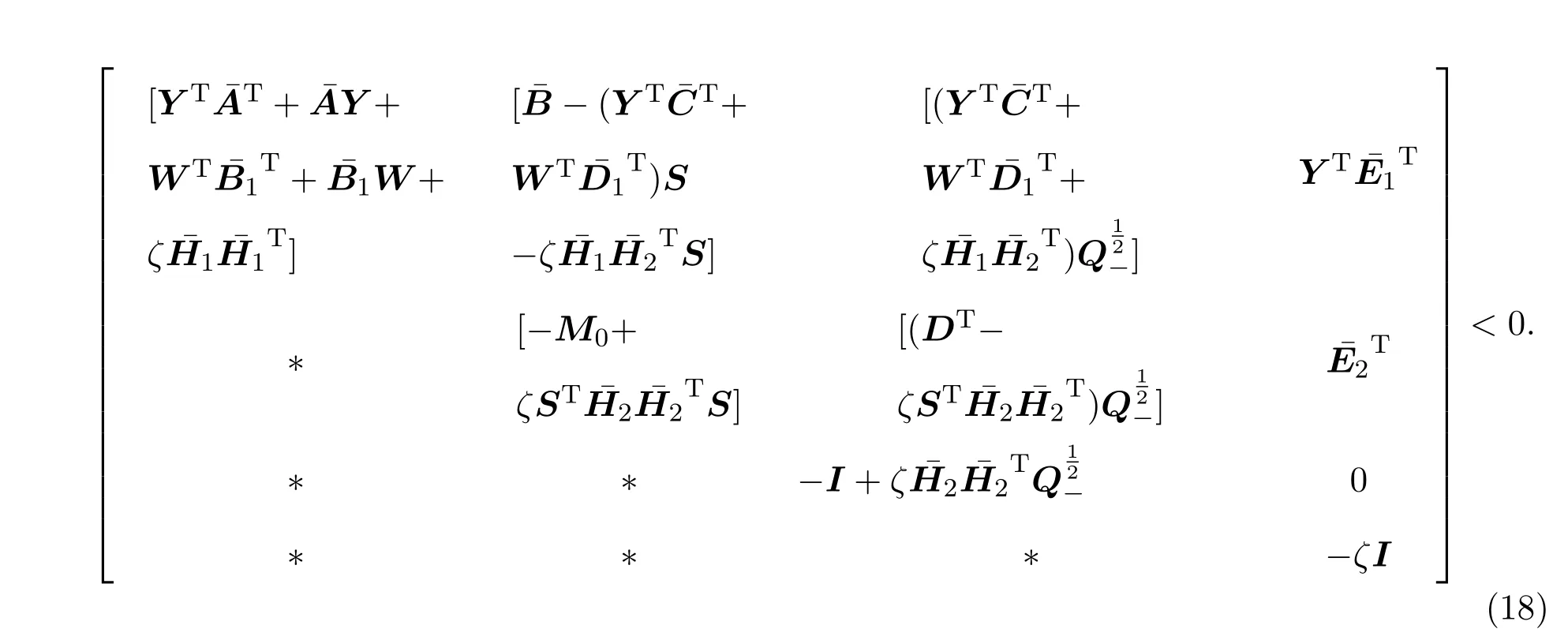
如果矩阵不等式(17),(18)存在一个可行解Y 和W,则

为一个状态反馈的非脆弱PI控制器,且控制器增益的显示表达式由
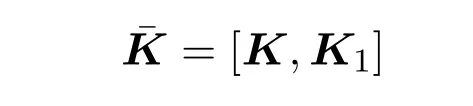
得到.
证明将闭环系统(16)代入引理4.1,根据定理4.1和Schur补引理即可得证.
5 数值算例
例 5.1采用文献[11]中的算例,考虑广义系统(1)选取参数矩阵为:
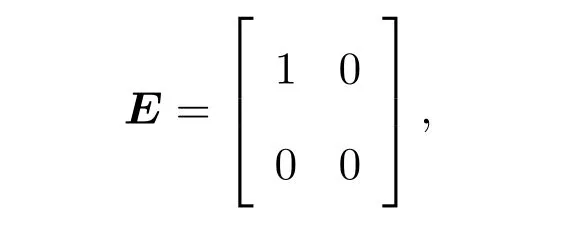

将已知矩阵代入式(9)求得增广闭环系统系数矩阵,再代入定理1中的矩阵不等式(10),(11),利用MATLAB中的LMI工具箱,求得可行解
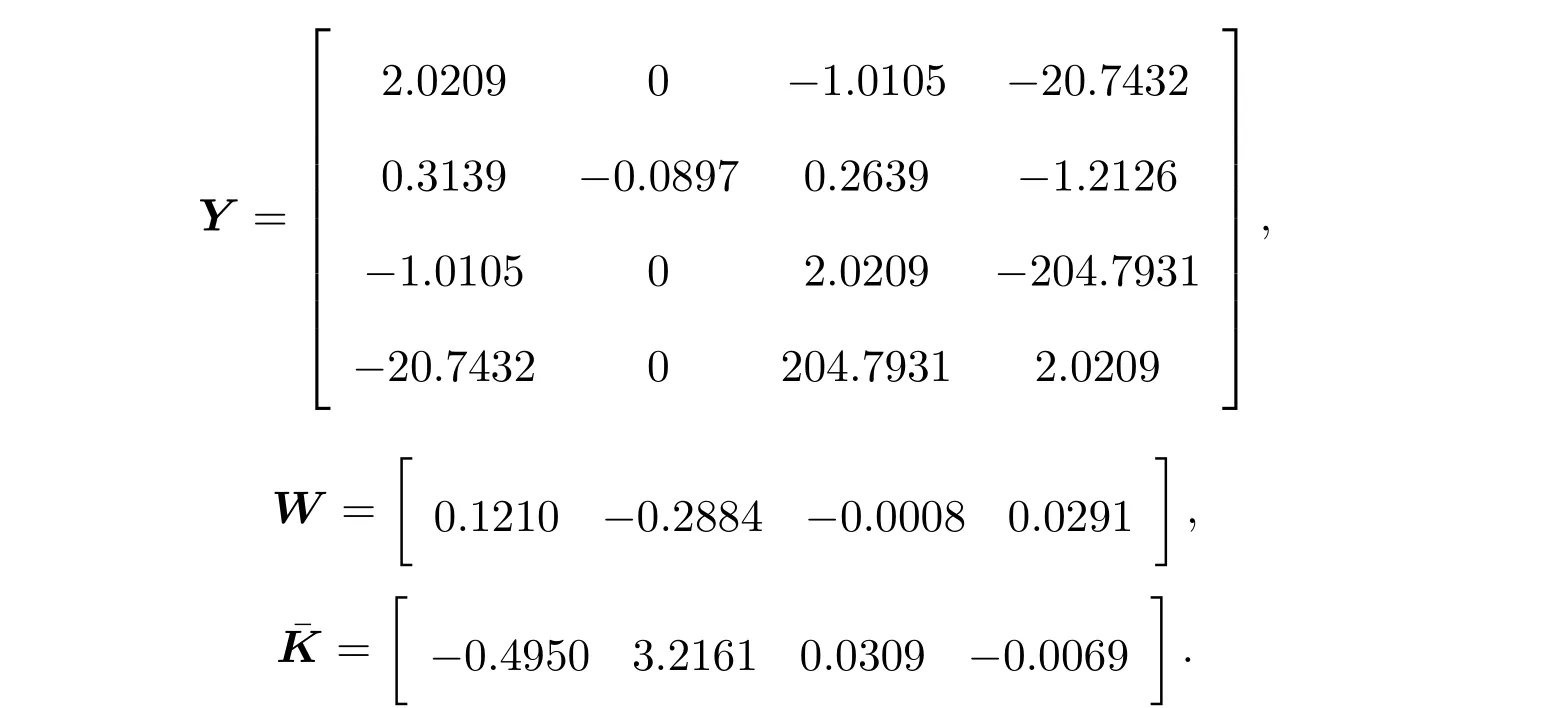
此时的控制器为
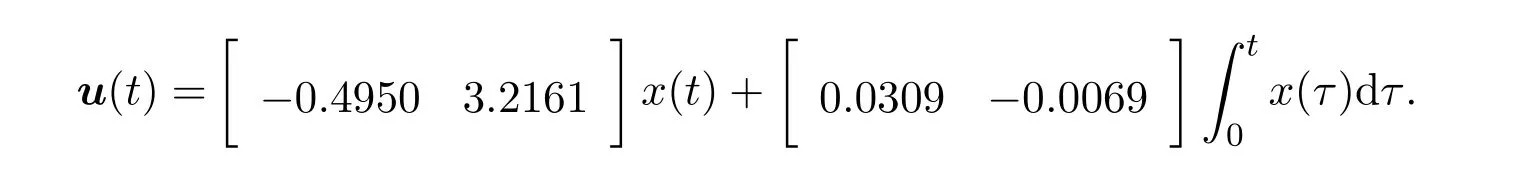
例 5.2 在例1的基础上考虑不确定广义系统(12),选取不确定性参数为
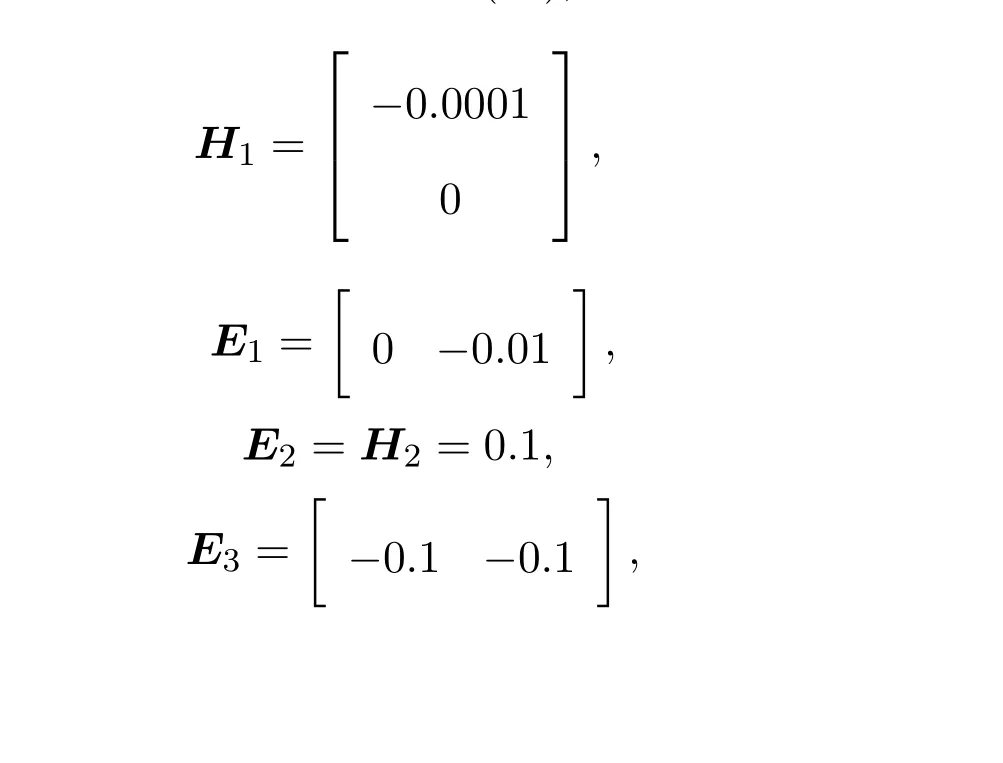
代入式 (16)求得增广闭环系统系数矩阵,再代入定理 2中的矩阵不等式 (17),(18),利用MATLAB中的LMI工具箱,求得可行解

此时的PI非脆弱控制器为:
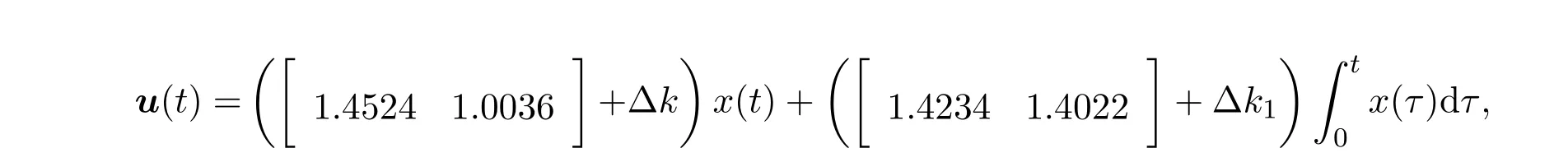
其中∆K,∆K1为满足(14)式约束条件的扰动.
6 结论
本文主要研究了不确定广义系统基于非脆弱PI控制器的严格耗散控制问题.分别给出了不确定广义系统的PI控制器和非脆弱PI控制器存在的充要条件及相应的设计方法,在所设计的控制器下,闭环广义系统容许且严格耗散.值得指出的是,本文给出的系统增广方式较为灵活巧妙,使得设计出的控制器为小增益控制器,更利于节约成本.
[1]董心壮,张庆灵.线性广义系统的鲁棒严格耗散控制[J].控制与决策,2005,20(2):195-198.
[2]董心壮,张庆灵.滞后离散广义系统的鲁棒严格耗散控制[J].控制理论与应用,2005,22(5):743-747.
[3]Masubuchi I.Output feedback controller synthesis for descriptor systems satisfying closed-loop dissipativity[J].Automatica,2007,43(2):339-345.
[4]张玉,董心壮.线性广义系统基于观测器的严格耗散控制[J].计算技术与自动化,2009,28(2):13-18.
[5]苏晓明,肖梅娥.不确定时滞双线性广义系统的鲁棒耗散控制[J].控制与决策,2012,27(4):623-631.
[6]Yang Li,Liu Xinzhi,Zhang Zhigang.Dissipative control for discrete singular impulsive dynamical systems[C].2011 30th Chinese Control Conference(CCC),2011:203-207.
[8]Lin Jinxing,Yang Shi,Fei Shumin,et al. Reliable dissipative control of discrete-time switched singular systems with mixed time delays and stochastic actuator failures[J].Control Theory Applications,2013,7(11):1447-1462.
[9]Xie S L,Xie L H,Souza C E.Robust dissipative control for linear systems with dissipative uncertainty[J].Int.J.of Control,1998,70(2):169-191.
[10]王淑平,张国山.基于PI控制器的线性系统的鲁棒耗散控制[J].控制与决策,2012,27(8):1139-1144.
[11]Li Hong,Shi Shuhui.Non-Fragile Dissipative Control for Uncertain Singular Systems via PD Controller[C].2016 28th Chinese Control and Decision Conference(CCDC).china:shenyang,2016:257-260.
Non-fragile dissipative control for uncertain singular systems via PI controller
Li Hong
(Basic Course Department,Shenyang Institute of Technology,Fushun 113122,China)
The question of dissipative control is considered for a class of singular systems with uncertainty,the necessary and sufficient condition of admissible and strictly dissipative is given by using linear matrix inequality.A non-fragile state feedback PI controller is designed by using the solution of linear matrix inequality such that the closed-loop system is both admissible and strictly(Q,R,S)dissipative for all the uncertainties.At last,numerical examples show the correctness and e ff ectiveness of the proposed method.
singular systems,strictly dissipative,PI controller,non-fragile control
O23
A
1008-5513(2017)04-0331-09
10.3969/j.issn.1008-5513.2017.04.001
2017-05-10.
辽宁省教育厅科学研究一般项目(L2015381).
黎虹(1981-),硕士,副教授,研究方向:广义系统的耗散控制.
2010 MSC:94A15
