桥上CRTS Ⅱ型板式无砟轨道均匀温度研究*

戴公连，杨凌皓，朱俊樸，苏海霆

(中南大学 土木工程学院，湖南 长沙 410075)

桥上CRTS Ⅱ型板式无砟轨道均匀温度研究*

戴公连，杨凌皓，朱俊樸†，苏海霆

(中南大学 土木工程学院，湖南 长沙 410075)

在某客运专线曲线段桥上设置温度传感器，通过对CRTS Ⅱ型板式无砟轨道进行长达两年的监控，得到其时变规律，利用时间序列差分法求得测点日平均温度，得到代表整体温度变化趋势的均匀温度时程曲线，有效反映了结构温度随大气的季节性变化规律.基于傅立叶曲线拟合及高阶矩统计模型研究其规律，提出无砟轨道整体的均匀温度变化规律.结果表明,结构各测点均匀温度呈现以365 d为周期的三角函数变化规律，其拟合参数可分别表示均匀温度变化规律中的中位值、幅值及相位差；各测点间的均匀温度拟合结果差异较小，可将轨道全截面作为一整体分析，用其统一温度代表轨道整体的均匀温度变化规律；通过高阶矩概率统计模型对统一温度分析，可得到具有概率保证的均匀温度变化方程.

桥梁工程；铁道工程；轨道结构；温度作用；试验分析

无砟轨道因其整体性好、稳定性高、刚度大、维修少等优点，现已成为世界高速铁路轨道结构发展趋势[1].我国通过引进与再创新，已经形成了适合我国路情的 CRTS Ⅱ型板式无砟轨道，并成功应用于京津、京沪、沪杭、沪昆等多条高速铁路中[2].由于“连续式”的结构特点，Ⅱ 型板对温度作用较为敏感，温度作用可使其出现变形，甚至可能产生结构裂缝，刚度降低，滑动层破损等危害[3].因此，为保证高速铁路的安全与舒适，温度对无砟轨道的作用不可忽略.

一般来说，混凝土结构受到日照作用、骤然降温作用和年温度作用3种温度影响[4].而国内外学者主要研究由于日照产生的温度梯度作为混凝土结构的主要作用，对年温度的作用讨论较少[5-8].我国现行高速铁路设计规范提出了在无砟轨道设计时，需根据当地气象条件，考虑年温度作用，但并未给出其具体如何取值、取多大值[9].文献[10]虽具体分析了年温度作用与其他荷载进行组合时，Ⅱ型板的相应性能情况，但在具体取值时，仅将结构整体升、降温10 ℃作为年温度作用；文献[11]将最高月和最低月的平均温度作为年温度变化的两个幅值.而在实际应用中，为保证高速铁路轨道平顺性，不仅需要掌握轨道温差的极值情况，还应掌握温度的时变规律以得到结构变形的时变规律.显然，上述文献中对年温度作用的取值方法难以反映真实情况，因此，有必要对无砟轨道年温度作用的取值方法做进一步的研究.

本文以某客运专线曲线段桥上CRTS Ⅱ型板式无砟轨道为研究对象，对其进行多达2年的温度监测，建立时程曲线，为研究其年温度时变规律，用差分法处理数据，从原始温度剥离日照等因素引起的波动温度，得到反映测点整体趋势规律的均匀温度时程曲线；并利用傅立叶曲线拟合对时程曲线进行拟合，得到结构均匀温度变化规律；对轨道内所有测点平均处理，建立该结构的统一均匀温度；使用高阶矩统计方法对均匀温度时程曲线与拟合曲线的差值分析，提出一定超越概率保证下相应的温度极值曲线.

1 CRTS Ⅱ型无砟轨道温度监测系统

以某客运专线曲线段桥上CRTS Ⅱ型板式无砟轨道为研究对象，测试其各测点温度随时间变化情况，监测系统位于北纬28.47°，东经117.97°，亚热带季风性湿润气候.采用BGK-3700电阻式温度计采样，仪器误差为±0.2 ℃；采样周期为0.5 h，每日采集48个温度数据.监测时间从2013年10月5日0时轨道完成铺设开始至2015年10月31日23时30分.测点布置如图1所示.

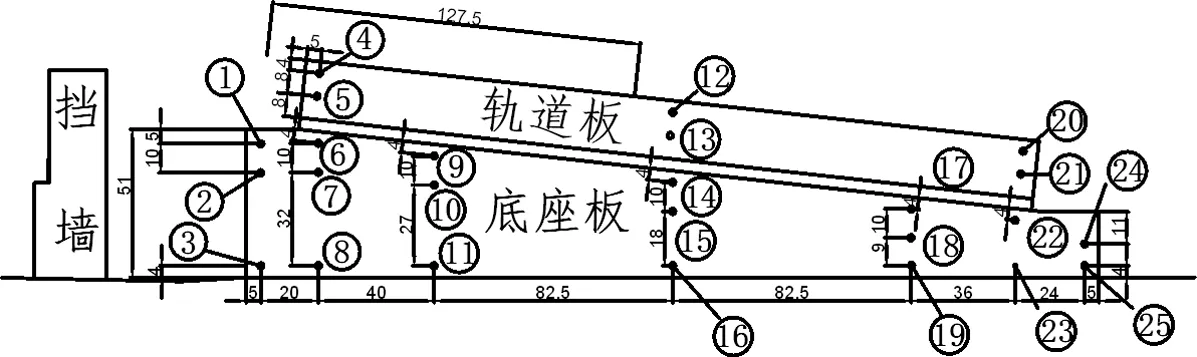
图1 温度监测系统测点布置图Fig.1 Arrangement of thermal sensors in track

2 均匀温度曲线的建立

为了保证高速铁路在使用时的舒适性，掌握轨道的变形规律至关重要，因此，除了确定结构温度作用的极值外，还必须掌握温度随时间的变化规律.为此，笔者根据监测系统采取的温度数据，以日期为横轴，测点温度值为纵轴，绘制相应的时程曲线加以研究.

对于本轨道结构的任一温度测点，其时程曲线均包含了趋势变化和短期波动变化的两种温度变化成分.趋势变化表示的是在季节性的气候变化下，结构测点温度随大气年温度的变化规律，反映了温度时程曲线的整体走势，是结构的年温度作用变化规律.短期波动变化表示的是结构测点温度在以日照为主要影响因素的作用下或是受到剧烈天气变化影响下，以日为周期发生的升、降温过程，在时程曲线上表现为具有一定规律的上下波动的“毛刺”.不过，这种波动规律由于受日照、风向与风速、剧烈天气变化等多种因素影响，很难单从本时程曲线进行分析，也并非结构年温度作用所研究的内容，因此本文不对此进行深入讨论.

以轨道板顶缘号12号测点为例，其监测温度的时程曲线如图2所示.

日期图2 测点12温度监测时程曲线Fig.2 Time-varing curve of point 12

从图2看出，在监测中由于仪器故障等原因而产生部分数据缺失，具体可分为：个别数据缺失和连续天数缺失.对于前者，采用拉格朗日插值法补充数据；对于后者，从图2中可看出,时程曲线在宏观上其温度变化的整体趋势规律表现为：夏季温度高，冬季温度低，整体变化大致呈三角函数变化，有明显的年周期性.因此，连续天数数据缺失并不影响温度变化的整体规律，即均匀温度变化的研究.

为尽可能排除“毛刺”的影响，将监测数据时程曲线的趋势变化和短期周期变化进行分解，在此采用时间序列差分法：以日为周期，对原始数据序列差分分解，得出其趋势变化的时程曲线.

由于在数据差分中使用了均匀处理的方法，因此可将结构温度的整体趋势变化的时程曲线定义为均匀温度曲线.得到的12号测点均匀温度曲线如图3所示.

日期图3 测点12的均匀温度曲线Fig.3 Uniform temperatrue curve of point 12

显然，图3的均匀温度曲线反映了图2时程曲线的整体趋势，并基本消除了波动温度产生的“毛刺”，其规律大致符合正弦变化.

将图2的原始温度减去图3的均匀温度，可得到被剥离出的波动温度，其表示结构受到日照等因素产生的以日为周期的温度升、降温过程，如图4所示.

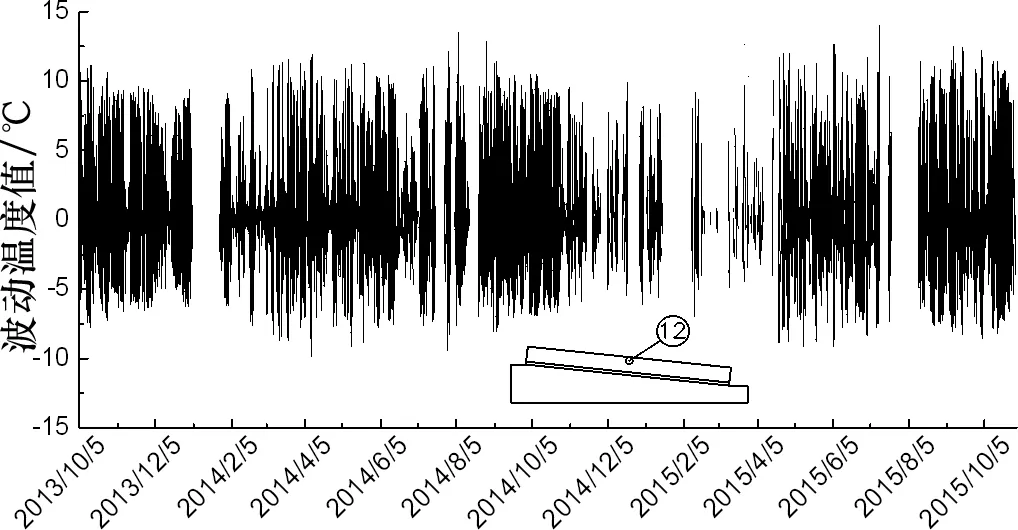
日期图4 测点12的波动温度曲线Fig.4 Fluctuating temperature curve of point 12

由图4可看出，波动温度总是在零线附近进行周期性的波动，符合时间序列分离的结果，从而从另一方面证明了均匀温度曲线的正确性.

3 均匀温度曲线的傅立叶拟合

3.1 傅立叶曲线拟合

若直接对测点均匀温度曲线进行拟合，其拟合优度可能不理想.经过分析，测点均匀温度曲线并不是很光滑，仍存在一定的上下波动.因此，有必要在拟合之前，在不改变整体变化规律的前提下，对其进行一定的平滑处理，以减小波动影响，提高拟合精度.

这里采用局部多项式估计法，简称Lowess法[12-13].根据数据误差大致服从正态分布，选用三次权函数[14]；利用目标规划，选取平滑点数r=28.

下面进行傅立叶曲线拟合.据上文所述，图3的测点均匀温度时程曲线反映了测点的年温度变化规律.为量化规律，得到具体方程表达式，有必要对其曲线进行拟合.由于曲线大致呈现正弦变化，因此利用傅立叶级数拟合，其中傅立叶级数表达式为：

(1)

式中:a0,an,bn和ω为傅立叶曲线拟合参数.

根据式(1)对各测点拟合，发现ω的取值在0.017 0～0.017 4中变化.而根据天体运动和气候关系，大气年温度的周期变化与太阳直射点在南北回归线之间的运动有关，周期为一回归年，即365 d，即大气年温度T=365.又大气温度与混凝土温度变化具有相同频率[15]，即结构温度变化周期也为T=365 d，因此对式(1)而言，可取圆频率ω=2π/365=0.017 2.在此基础上，对均匀温度时程曲线进行傅立叶级数拟合，各测点均满足拟合精度要求.

以测点12为例，得到的平滑曲线和拟合曲线如图5所示.

日期图5 测点12平滑处理与傅立叶拟合Fig.5 Smoothing curve and Fourier fitting curve of point 12

3.2 傅立叶曲线拟合阶数的影响

增大傅立叶曲线拟合的阶数，能提高拟合精度，但也要避免出现过拟合.以测点12为例，1—5阶拟合结果如表1所示.

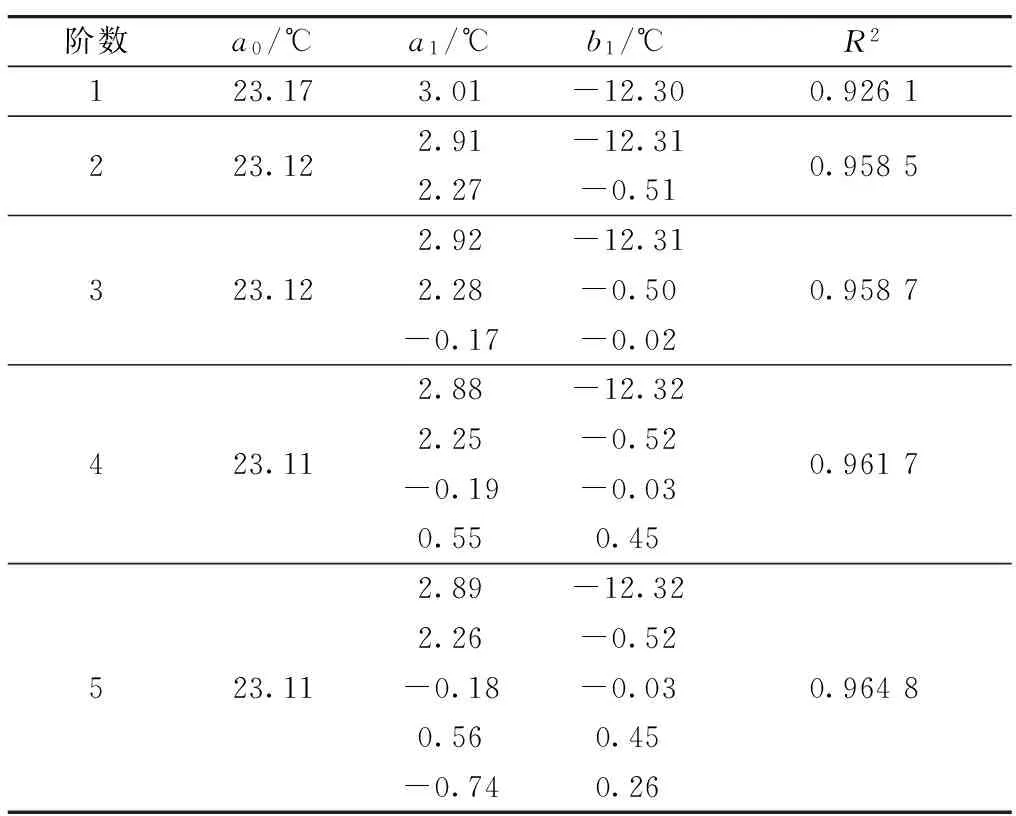
表1 测点12傅立叶曲线1—5阶拟合结果

从表1可看出，1阶到5阶R2均大于0.9，满足拟合要求，但其拟合参数a0,a1,b1相差并不大，1阶与5阶仅相差0.06 ℃,0.12 ℃,0.02 ℃，显然对于工程设计而言，1阶的傅立叶曲线拟合已能满足工程精度.并且1阶傅立叶拟合对后文确定均匀温度方程式各参数的物理含义更加直观.

3.3 均匀温度拟合方程物理含义分析

根据表1，测点12均匀温度拟合方程表示为：

T(t)=23.17+3.01cos(0.017 2t)-

12.30sin(0.017 2t)

(2)

根据三角函数变换公式，有

(3)

另外，为便于分析，令1月1日为时间原点，即t=1，则式(2)可化为：

T(t)=23.17-12.30cos[2π(t-16)/365]

(4)

根据三角函数的含义，可知均匀温度曲线方程的一般规律有：

T(t)=Tmean-ΔTcos[2π(t-φday)/365]

(5)

式中：Tmean为均匀温度曲线中位值；ΔT为均匀温度曲线变化幅值；φday为均匀温度最大值距1月1日的天数.

4 无砟轨道统一温度的建立

依据第3节所述方法，可得到各测点的均匀温度拟合方程.为研究轨道内竖向、横向均匀温度变化规律及轨道板、底座板之间的差异，现在选取结构一竖向(12-13-14-15-16)及一横向(6-9-14-17-22)测点，分别定为A组和B组.其拟合结果如表2和表3所示，均匀温度变化如图6所示.

表2 A组测点拟合结果

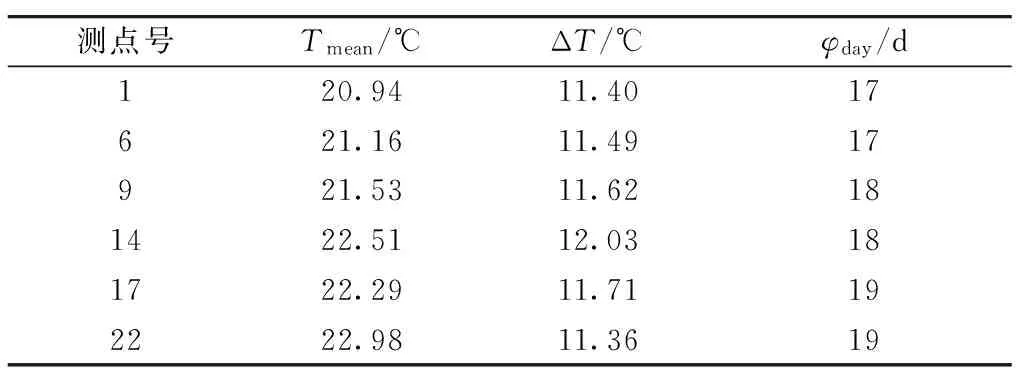
表3 B组测点拟合结果

日期(a)A组测点均匀温度曲线

日期(b)B组测点均匀温度曲线图6 无砟轨道指定测点均匀温度曲线Fig.6 Uniform temperature curve of specific points

从表2和表3可以看出,各测点结果拟合均较为接近.其中：在竖向上，测点间Tmean,ΔT和φday的差值最大值分别为1.35 ℃,0.55 ℃和2 d，在工程应用中，这一误差可忽略，因此，可认为在竖向上不同测点的均匀温度基本一致；同理，在横向上，测点间Tmean，ΔT和φday的差值最大值分别为2.04 ℃，0.67 ℃和2 d，因此，也可认为在横向上不同测点的均匀温度基本一致.

在实际工程应用中，显然无法考虑每个测点各自的规律，若能进行整体性简化，则更便于设计与结构分析.考虑到各测点的均匀温度变化规律基本一致，故在此建立统一温度曲线.

统一温度曲线将一个区域内的温度值用取平均的方式统一化，即一个区域最终仅用一个温度曲线表示，表示为：

(6)

式中：Tu，k为k区域的统一温度；Ti为k区域第i号测点温度.

在本文中，由于是对各测点的均匀温度曲线做统一化处理，故将其称为统一均匀温度曲线(以下简称统一温度).

根据式(6)绘制轨道板、底座板及无砟轨道整体的统一温度曲线，如图7所示.

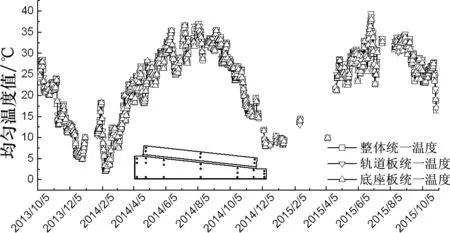
日期图7 无砟轨道统一均匀温度曲线Fig.7 Overall curve of track

由图7可知，3条曲线基本重合，其变化规律与各测点均匀温度曲线规律显然也一致，即随四季气温变化而呈现冬低夏高的趋势.故用第3节方法，经Lowess平滑及傅立叶曲线拟合后，得到对应的拟合参数值，结果如表4所示.

表4 无砟轨道统一温度拟合结果

三者拟合方程分别为：

Ttrack=22.73-12.40cos[2π(t-17)/365]

(7a)

Tbase=21.94-11.44cos[2π(t-19)/365]

(7b)

Twhole=22.17-11.65cos[2π(t-18)/365]

(7c)

从拟合结果可以看出，三者统一温度拟合结果相差很小，在1个单位以内.因此，可说明轨道板与底座板在均匀温度的特征规律上基本相近，故在一般设计上，为方便设计与结构分析，可用整体的统一曲线代表整个无砟轨道的均匀温度变化规律.

5 基于高阶矩法的均匀温度代表值计算

由图5可知，光滑的拟合曲线与均匀温度在同一时刻存在着一定的差值，以结构整体统一温度数据为例，在时间轴上绘出这一差值，如图8所示.

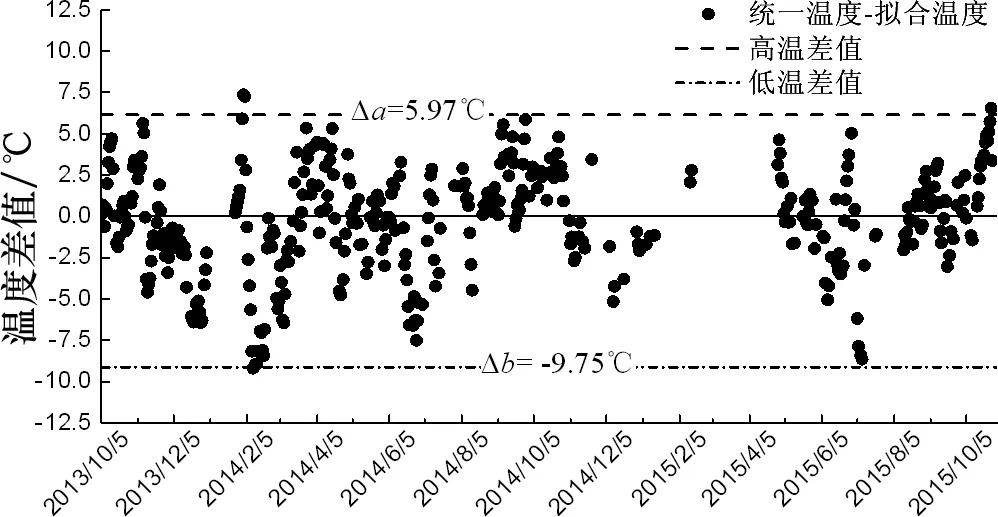
日期图8 统一温度-拟合温度差值示意图Fig.8 Differences between overall curve and fitting curve

由图8可知，这一差值代表总在零线附近波动且满足一定的分布规律，其表示的是均匀温度在时间上的随机性.对差值采用高阶矩法[16]进行统计分析，计算在超越概率1%即100年重现期下的值，可得正、负极值分别为：

Δa=5.97 ℃

Δb=-9.75 ℃

Δa=5.97 ℃表示在概率保证下，实际温度比整体统一温度Twhole高出的极大值，将Δa与式(7c)相加，可得到统一温度高温极值曲线；同理，Δb与式(7c)相加，可得到统一温度低温极值曲线.

Twhole,upper=28.14-11.65cos[2π(t-18)/365]

(8a)

Twhole,lower=12.42-11.65cos[2π(t-18)/365]

(8b)

将统一温度曲线与两条极值曲线绘制在同一图中，如图9所示.从图9中可看出，几乎所有的统一温度值都在两条极值曲线范围内，其表示在100年重现期下，无砟轨道统一温度极大值不会高于式(8a)，极小值不低于式(8b).显然，式(8)确立的无砟轨道统一均匀温度极值时程曲线可用于计算无砟轨道的轴向变形在不同季节可能发生的极值.其具有统计意义的极值曲线也能为工程设计提供参考.

日期图9 无砟轨道统一温度代表值Fig.9 Representative value of overall curve of track

6 结 论

1)对某客运专线曲线段CRTS Ⅱ型板式无砟轨道以半小时为采样频率，进行长达两年的温度监测.采用时间序列分析理论中的差分法分析，得到代表整体温度变化趋势的均匀温度曲线和以日为周期在零线附近上下波动的波动温度曲线.从图2可看出，结构的均匀温度随大气温度季节性变化而大致呈正弦规律.

2) 为提高拟合精度，采用Lowess法对均匀温度数据平滑处理，并以一回归年即365日为周期，对均匀温度曲线进行傅立叶拟合，以12号测点为例得到拟合方程.

3) 采用1—5阶傅立叶曲线拟合，其1—5阶的拟合优度R2均大于0.9，满足拟合要求，但1阶与5阶拟合结果相差不大，不超过0.12 ℃，说明1阶拟合已满足实际工程设计的需要；对1阶拟合结果利用三角函数变换可简化拟合结果，得到三角函数形式的无砟轨道均匀温度方程：T(t)=Tmean-ΔTcos[2π/365(t-φday)].

4)各测点拟合结果相差不大，用统一化方法，分别对轨道板、底座板及无砟轨道结构整体进行统一温度分析，得到的拟合方程见式(7)，三者统一温度规律相近，在实际应用中，可用轨道整体统一温度表示该无砟轨道的均匀温度变化规律.

5)监测得到的均匀温度与傅立叶拟合曲线存在一定差值，经过分析该差值总在零线附近波动，满足一定的规律.对这一差值用高阶矩的统计方法分析，得到超越概率1%下正、负极值分别为Δa=5.97 ℃，Δb=-9.75 ℃，将其与式(7c)相加，可得到超越概率1%下统一温度极值曲线(8)，其结果显示了无砟轨道均匀温度变化的基本规律，可用于计算结构的轴向变形在不同季节可能发生的极值；而具有统计意义的极值曲线也能为工程设计提供参考.

[1] SUN L，CHEN L L，ZELELEW H H.Stress and deflection parametric study of high-speed railway CRTS-Ⅱ ballastless track slab on elevated bridge foundations[J].Journal of Transportation Engineering，2013，139(12):1224-1234.

[2] 吴斌，陈文荣，刘参，等.列车竖向荷载下CRTSⅡ型板式无砟轨道结构受力特性试验研究[J].铁道科学与工程学报，2014,11(3)：37-42.

WU Bin，CHEN Wenrong，LIU Can，etal.Experimental study on mechanical characteristics of CRTSⅡ slab track under the vertical load of train[J].Journal of Railway Science and Engineering，2014，11(3)：37-42.(In Chinese)

[3] 张志超，曾志平，元强，等.温度荷载作用下桥上CRTS Ⅱ型板式轨道纵向力学特性研究[J].铁道科学与工程学报，2015,12(5):982-989.

ZHANG Zhichao，ZENG Zhiping，YUAN Qiang，etal.Study on longitudinal mechanical characteristics of CRTS Ⅱ slab track on bridge under the temperature load[J].Journal of Railway Science and Engineering，2015，12(5):982-989.(In Chinese)

[4] 刘兴法.混凝土结构的温度应力分析[M].北京:人民交通出版社，1991：10-13.

LIU Xingfa.Analysis of thermal stress of concrete structures [M].Beijing：China Communications Press,1991:10-13.(In Chinese)

[5] THOMAS N S.Temperature efeects in concrete box girder bridges [D].Calgary：School of Civil Engineering，University of Calgary，2004:3-50.

[6] LI D N，MAES M A，DILGER W H.Evaluation of tempera-ture data of confederation bridge：thermal loading and movement at expansion joint [C]∥Proceedings of the 2008 Structure Congress．Alberta，Canada：ASCE，2008:314 -324．

[7] 戴公连，苏海霆，闫斌.秋季桥上纵连板式无砟轨道竖向温差试验研究[J].湖南大学学报：自然科学版，2015，42(3)：94-99.

DAI Gonglian，SU Haiting,YAN Bin.Experiment study on the vertical temperature gradient of longi-tudinally connected slab ballasteless track on bridge in autumn[J].Journal of Hunan University:Natural Sciences，2015，42(3):94-99.(In Chinese)

[8] 欧祖敏，孙璐，程群群.高速铁路无砟轨道温度场简化计算方法[J].浙江大学学报:工学版，2015，49(3)：482-487.

OU Zumin，SUN Lu，CHENG Qunqun.Smiplified calculation method on nonlinear temperature effects of high-speed railway ballastless track slab[J].Journal of Zhejiang University:Engineering Science，2015，49(3)：482-487.(In Chinese)

[9] TB10621-2014 高速铁路设计规范[S].北京：中国铁道出版社，2015:81.

TB10621-2014 Code for design of high speed railway[S].Beijing：China Railway Press，2015:81.(In Chinese)

[10]班霞.温度作用下CRTS Ⅱ型无砟轨道结构体系的性能分析[D].长沙：中南大学土木工程学院，2012:42-45.

BAN Xia.Analysis of the performance of CRTS Ⅱ slab ballastless track structure under temperature [D].Changsha：School of Civil Engineering，Central South University，2012:42-45.(In Chinese)

[11]朱晓嘉.CRTS Ⅱ型轨道板温度效应及其对列车运行安全性的影响分析[D].成都：西南交通大学土木工程学院，2012:9-10.

ZHU Xiaojia.Analysis on CRTS Ⅱ track slab temperature effects and its influences on the running safety of the vehicle [D].Chengdu：School of Mechanical Engineering，Southwest Jiaotong University，2012:9-10.(In Chinese)

[12]黄喻.Lowess方法在同位素地层学中的应用[D].成都:成都理工大学信息管理学院，2007:14-20.

HUANG Yu.The application of Lowess fit to isotope stratigraphy [D].Chengdu：School of Information Management，Chengdu University of Technology，2007:14-20.(In Chinese)

[13]YANG Junwei.Thermal time-constant spectrum extraction method in AlGaN/GaN HEMTs [J].Journal of Semiconductors,2015，36(8)：084003-1-084003-6.

[14]董芳英，张帼奋.基因芯片数据标准化局部加权回归法权函数探究[J].浙江大学学报:理学版，2010，37(1)：22-29.

DONG Fangying，ZHANG Guofen.Normalization for microarray data：the weight function of local weight regression [J].Journal of Zhejiang University :Science Edition，2010，37(1)：22- 29.(In Chinese)

[15]刘鹏，余志武，宋力.自然环境温度作用谱和混凝土温度响应谱[J].建筑材料学报，2014，17(3)：532-537.

LIU Peng，YU Zhiwu,SONG Li.Spectra of temperature action and response of concrete in natural environment [J].Journal of Building Materials，2014，17(3)：532-537.(In Chinese)

[16]朱俊樸，戴公连，苏海霆，等.基于高阶矩法的高铁梁-轨系统温度作用代表值研究 [J].东北大学学报：自然科学版，2017,38(8)：1-6.

ZHU Junpu，DAI Gonglian，SU Haiting,etal. High speed railway box girder-track temperature action representative values research based on higher-order moment method [J].Journal of Northeastern University:Natural Science,2017,38(8):1-6.(In Chinese)

Research on Uniform Temperature of CRTS Ⅱ Slab-typeBallastless Track on Bridge

DAI Gonglian，YANG Linghao，ZHU Junpu†，SU Haiting

(School of Civil Engineering，Central South University，Changsha 410075，China)

Thermal sensors have been installed on a curved bridge of high-speed rail.By means of carrying out 2 years monitor of CRTS II ballastless track，the time-varing rules are revealed.Through daily temperature data calculated from the measured data by using difference method of time series，the time-varing curve of uniform temperature，which represents the trend of bulk temperature change laws，can be obtained.Then，the rules of track temperature variance with atmospheric temperature are effectively reflected.In order to examine the change law of uniform temperature，Fourier curve fitting and high-moment statistical model are utilized，and the overall curve representing the changing laws of track temperature are put forward.The results show that the track uniform temperature appeared trigonometric development with a tropical year (namely 365 days) as a cycle，and the regression parameters can represent its median，amplitude and phase-difference.The entire section of the track can be analyzed as a whole，because the fitting results among test points are close，which indicates that the changing laws of track uniform temperature can be expressed by its overall curve.By using high-moment statistical model to analyze the differences between overall curve and its fitting curve，the representative value of overall curve with probabilistic guarantee can be obtained.

bridge engineering; railroad engineering; track structure; temperature action；experimental analysis

1674-2974(2017)07-0136-07

10.16339/j.cnki.hdxbzkb.2017.07.017

2016-04-05

国家自然科学基金资助项目(51378503) , National Natural Science Foundation of China(51378503)；中国铁路总公司科技研究开发计划资助项目(2015G001-K)，Project of Science and Technology Research and Development Program of China Railway Corporation(2015G001-K)；中南大学中央高校基本科研业务费专项资金资助项目(2017ZZTS532)，Fundamental Research Funds for the Central Universities of Central South University(2017ZZTS532)

戴公连(1964—)，男，河南夏邑人，中南大学教授，博士生导师†通讯联系人， E-mail：zhujunpu@gmail.com

U24

A