大跨空间结构选形优化方法比较研究*

刘霞，郭立君，易伟建

(湖南大学 土木工程学院，湖南 长沙 410082)

大跨空间结构选形优化方法比较研究*

刘霞†，郭立君，易伟建

(湖南大学 土木工程学院，湖南 长沙 410082)

为了确定某大跨空间结构的最佳受力体系，结合结构形态学知识，根据ESO方法的基本原理，以有限元分析软件ANSYS为平台，建立初始设计域的三维实体模型，以每个单元的存活状态为设计变量，以结构体积最小为目标函数，对该大跨空间结构进行了结构受力体系的选形优化.为满足建筑意图及特殊基础条件的限制，最终选形结果确定为钢结构拱支承受力体系.最后，将ESO方法选形优化确定的结构受力体系与原设计院逆吊法选形优化确定的结构受力体系进行静力计算变形和内力的对比分析，说明了ESO方法选形结果比逆吊法选形结果具有优越性，验证了ESO方法对大跨空间结构受力体系选形优化的可行性及高效性，同时得出了拓扑优化方法对大跨空间结构受力体系选形优化的重要性和必要性.

大跨空间结构；选形优化；ESO方法；逆吊法；结构形态学；可靠性分析

随着科学技术的发展和人民生活水平的提高，大跨空间建筑越来越受到关注，尤其是大跨空间的公共建筑，充分展示出结构技术的最新成就与结构造型的魅力.纵观世界，国内外的大型公共建筑都是以大跨空间结构为前提的，从直接关系人民身心健康的体育建筑，到促进信息交流的博览建筑，再到规模巨大的交通建筑、娱乐设施、剧场音乐院等，这些大规模的公共建筑都需要大跨度的结构体系来支撑[1].

结构受力体系的合理性至关重要，大跨空间结构受力体系的合理性是建立在对结构形态正确选择的基础之上.随着计算机技术的迅速发展，越来越多的研究人员开始运用优化方法对结构的形态进行优化设计.Bletzinger等[2]对基于物理选形原理的数值模拟方法进行了系统研究，并成功实现了逆吊实验法和肥皂薄膜实验的数值选形，而且对面内存在预应力的自由曲面壳体结构进行了选形研究.2009年，张晋芳等[3]探讨了将ESO方法用于厚板转换层的结构拓扑优化及选形研究，针对优化结果提出了两种新型的转换板形态，并对其进行了静力、动力受力性能分析和结构经济性效益评价.2010年，杨海军等人[4]运用ESO方法对位移约束下的预应力钢结构体系进行了选形优化，建立了以索力值和结构拓扑为设计变量的刚度最大结构的寻优，优化结果与相应的体系受力性能吻合，印证了ESO方法选形优化的可行性，并为今后预应力钢结构选形提供了依据.2012年，王磊等[5]运用非均匀有理B样条方法对曲面结构形态进行优化设计，通过对世博轴阳光谷以及上海交响乐团排演厅两个自由形态曲面的优化实例，证明了该方法的可行性及高效性.2014年，谢亿民等人[6]揭示了ESO方法在建筑设计中的重要性，指出了该方法可以有效地用于西班牙圣家族大教堂、大跨步行桥、壳体结构、周期性壳体结构等的选形，而且正逐步开发易于建筑师进行结构形态概念优化设计的软件，从而实现建筑与结构的一体化设计.2014年，阴书玉等[7]运用ESO方法对深孔机床床身进行了轻量化设计，使得优化后的床身整体质量减少了14.47%，从而有效实现了工程的应用价值.

结构选形优化方法的发展，为实现大跨空间结构多样复杂的结构形态提供了依据.结构选形是对结构最佳受力体系的优化选择.结构受力体系的选择是一个综合性很强的决策问题[8]，它对结构的强度、刚度、稳定性、动力特性、造价、美学效应等有众多要求，需要工程师在结构选形[9]的初期就要充分把握好结构整体的概念设计思想，运用高效、可靠的优化分析方法对结构整体进行选形优化，以达到安全可靠、经济合理和技术先进等要求.

1 优化方法的选择

经过多年的发展和完善，一些通用的结构优化操作方法已经建立并得到广泛认可,在这些方法中，逆吊实验法、ESO方法、改进进化论法、非均匀有理B样条方法、充气薄膜法等在结构的选形优化方面都有不同程度的应用.

逆吊实验法[10]是利用了柔性结构在特定荷载作用下只受拉力的特点，确定结构的形状，再通过对结构模型进行固化翻转，获得在重力荷载作用下的纯压结构.从结构形态学的角度看，逆吊实验法的本质是实现零弯矩结构(或称为小弯矩结构).最初的逆吊实验法多是基于模型试验的方法，对结构进行形态选择；随着计算机技术的发展，数值分析[11]与逆吊实验法的结合被广泛应用.

非均匀有理B样条方法[12]是建立自由曲线、自由曲面形状选形优化的较先进有效的数值分析方法[13].该方法基于应变能的选形优化准则，以给定条件下整体结构的应变能最小作为自由曲面优化选形的目标函数[14]，对初始建筑曲面造型进行优化设计，得到的曲面结构以薄膜应力为主，保证曲面达到“薄”而“刚”的最优建筑造型.这些方法在结构选形优化方面发挥了重要作用，不少学者已将其应用到了大跨空间结构的选形中.

ESO方法最早是由澳大利亚的Xie和Steven共同提出的[15]，这种方法基于一个简单的准则[16]：在不显著影响结构整体性和基本形态的前提下，逐渐删掉结构中利用率不高的材料，最终得到一个最优拓扑构形[17].由于ESO方法所依据的准则简单而且可以通过有限元分析软件平台来实现[18]，所以该方法很快便得到了广泛应用[19].近几年也出现了在大型工程结构选形设计中应用ESO方法的案例，其中最早的尝试是日本的芥川河畔办公楼[20](Akutagwa River Side Project)，其在西、南、北3个立面的设计中都应用了ESO的拓展算法.

因此，本文主要针对原利用逆吊法进行结构受力体系选形的某大跨空间结构，采用ESO方法，利用ANSYS有限元软件平台上的优化设计功能对其进行结构受力体系选形优化，对2种方法最终确定的结构受力体系进行静力计算分析，得出了优化方法对大跨空间结构受力体系选形优化具有指导意义的结论.

2 结构选形与结构体系的建立

2.1 工程概况

本工程以滑雪、滑冰为主而命名为冰雪世界[21]，拟建场地为一废弃的水泥厂矿坑(图1)，该矿坑平面呈 U 型开口，未支承的自由边横向跨度达200 m，地上部分最大建筑高度约40 m，总建筑面积达 117 500 m2.建筑的设计使用年限为50年，抗震设防烈度为6度，抗震设防类别为乙类.

(a) 矿坑现场照片

(b)屋盖效果图

(c)三维模型图图1 冰雪世界示意图Fig.1 Ice and snow world

冰雪世界为一椭圆盘状自由流线造型的建筑，有上、下两部分主体结构构成，见图1所示.上部主体为一大跨度空间钢网壳，下部主体是一个中间有近似60 m直径开洞的大平板；平板承担着上部主体结构的全部荷载，荷载的分布极具不均匀性，荷载值和分布情况见表1和图2所示.结合建筑造型及矿坑周边支承条件，需要通过选形优化设计选择合适的下部主体结构.

表1 荷载分布情况

注：分布区域1—7见图2所示；表中A，B，C代表恒载的种类.

(a)均布荷载分布区域

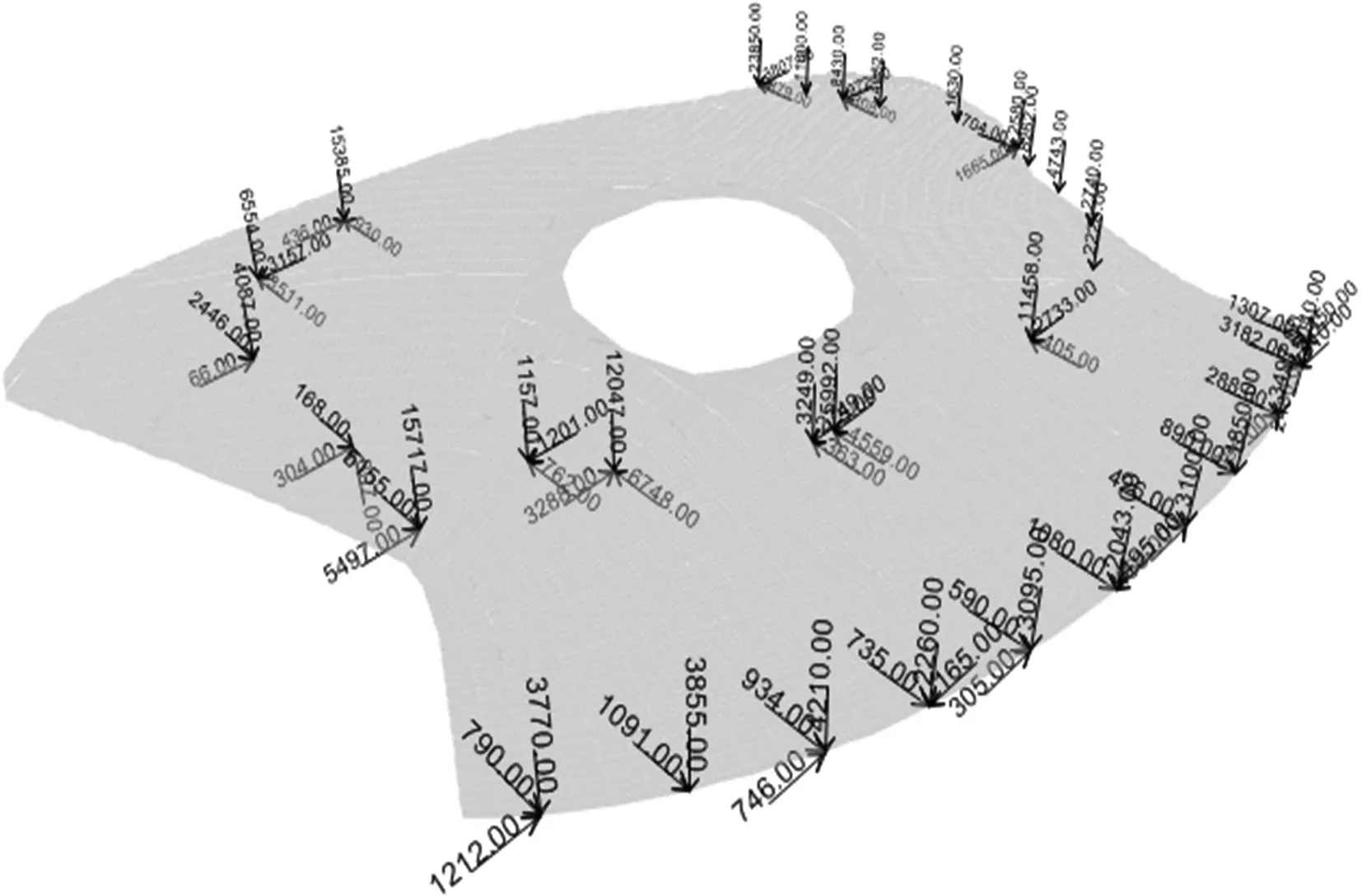
(b)集中荷载分布(单位：kN)图2 荷载分布情况Fig.2 Load distribution

2.2 基于逆吊法原理的选形

鉴于本工程的重要性及复杂性，设计院起初采用了逆吊法原理对下部主体结构进行了受力体系选形分析，拱面选形以初始平面、荷载分布、支座条件等为约束条件，基于逆吊原理和最低能量原理进行面外反向加载，找出拉应力流主要走向及分布范围，多次循环试算调整，最终得到假定荷载下弯曲应变能最小的曲面形状(图3).

图3 逆吊法选形基本过程示意Fig.3 Analysis procedure of inverse hanging method

整个选形流程包括如下步骤：

1)确定结构形态创建目标.

2)根据已知几何条件确定支承边界条件和形态控制条件.

3)创建初始曲面.

4)根据力学性能优化结构边界条件得到主应力迹线.

5)逆吊法创建曲面.

6)曲面离散化，沿主应力方向布置拱结构.

7)强制离散化单元满足形态控制条件，对拱结构布置的调整.

8)最终拱结构形态的确定.

在利用逆吊法进行选形优化时，值得注意的是楼面荷载分布的问题.对初始曲面施加荷载进行计算分析时，忽略了集中力的作用，只考虑了楼面均布荷载的分布，而且近似地将曲面分成4个不同荷载区域，按照一定的比例关系施加均布荷载，荷载的比例关系为A∶B1∶B2∶C=1∶3∶2∶2，如图4所示.

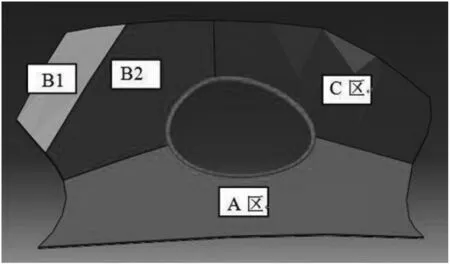
图4 逆吊法选形荷载分布图Fig.4 Load distribution of inverse hanging method

2.3 基于ESO方法的选形

ESO方法从包含所有设计的初始域出发寻优，本案例建筑和地基条件限定了下部主体结构的顶面和基础之间的最大允许高差为30 m，中部需开一近似直径60 m的圆洞，因此优化的初始设计域选定为如图5(a)所示的高30 m的中部开洞厚板，板的边界与周边地形吻合.有限元分析采用8节点的实体单元solid45单元建立初始设计域的三维实体模型，每个节点均具有3个自由度，即Ux,Uy,Uz3个平动自由度，单元的材料属性如弹性模量、泊松比等均依照混凝土材料来定义的；鉴于整个模型中间有一孔洞的存在，所以以中间孔洞为源面，采用体扫掠网格划分技术，扫掠整个模型生成体单元，而源面网格是由四边形网格组成，即扫掠生成的均为六面体单元.考虑到模型较大、三维结构受力复杂及软件的计算效率等问题，单元尺寸定为3 m.

(a)初始模型

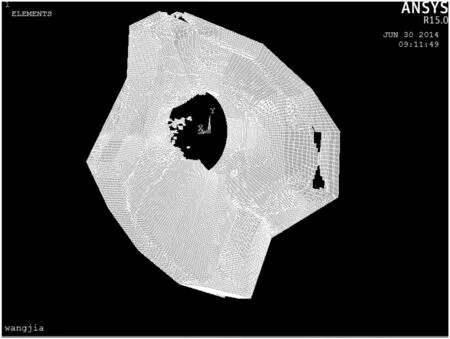
(b)优化后模型图5 三维实体ESO算法优化模型Fig.5 ESO computing results

在运用ESO方法选形优化中，删除单元的标准可以通过各单元对目标函数的贡献大小来衡量，即删除单元对目标函数贡献小的单元，保留贡献大的单元，这主要是借助目标函数的灵敏度分析来完成的.参考相关文献[22]，删除某单元时引起的目标函数的改变量称为目标函数的灵敏度，即定义单元的灵敏度为：

(1)

式中：Ki为第i个单元的刚度矩阵；ui为第i个单元的位移向量.

ESO方法选形的基本步骤为：1)给定结构初始设计域，指定单元类型和特性并将设计区域离散为有限元网格，在U型边界的三边施加约束；2)在楼面均布荷载和集中荷载作用下进行结构静力计算分析；3)提取各个单元信息，并按照式(1)计算控制截面单元的应变能；4)保留控制截面上具有最小应变能单元的信息，实现单元的删除操作；5)重复步骤2)—4)直到达到指定的体积比，迭代停止.图5为初始模型和优化后的模型.

由ESO方法优化结果(图5(b))可以看出，最终优化后的模型类似一个倒立的体育场看台，与穹顶结构形似.但由于是三维实体结构，单元为实体单元，模型大且单元重合遮挡，所以需要进一步操作分析来求得适合的结构受力体系.其具体操作步骤如下：

1)将ANSYS软件里的优化模型导入到CAD软件里面，把实体单元转化成直线，目的是易辨析和识别其结果，如图6所示.

图6 三维实体单元转化Fig.6 Transform of 3D solid element

2)结合模型受荷情况及优化结果，选取模型关键部位进行具体选形分析,采取的是样条曲线拟合点的方法进行曲线拟合，如图7所示.

3)根据曲线拟合结果，结合拱脚处建筑对标高的需求，采用曲线放样的方法生成曲面，如图8所示，该曲面即是ESO方法最终优化结果的类似体育场看台曲面.

4)精确分析曲面拟合结果，并结合基础U型开口、模型不规则、受荷不均匀等的特殊条件和建筑师对建筑效果的要求，决定下部主体结构采用钢结构拱支承受力体系，类似原设计方案，选取了3组主拱+板的钢结构拱支承受力体系，如图9所示.

图7 模型关键部位曲线拟合Fig.7 Curve fitting of model key positions

图8 拟合曲线生成拟合曲面Fig.8 Fitting surface by fitting curve

图9 拱支承钢结构受力体系Fig.9 The steel structural system of the supporting arch

在上述选形过程中发现，优化后的模型确实类似穹顶结构造型，由拟合得到的曲面可以看出，曲面壳体生成的控制点外壳线主要是沿径向方向(图10)，但由于U型边界一边开口且跨度大，使得直接沿径向方向传力体系的完整性削弱.因此，最后提出了类似原设计的环向三组拱支承的钢结构受力体系.

图10 曲面控制点外壳线Fig.10 The lines connecting surface control points

3 结构方案的分析比较

3.1 相同之处——结构构成

在建立的2种方案中，拱脚支撑在坑壁岩体上，在坑壁沿拱脚点的切线方向布置巨型钢筋混凝土基础，将荷载均匀扩散至岩石(图11).冰雪世界所需的结构楼面标高为-10.85 m，与拱脚的竖向最大距离近30 m，需要在拱上设置立柱及钢梁形成楼面，楼面板初步设计为200 mm厚的钢筋混凝土板，楼面板承担着屋盖及游乐区域的全部荷载.不同游乐区域的荷载要求差别较大，有明显的不均匀性，不均匀荷载作用下主拱结构受力不利，因此设置斜腹杆将上述梁柱构件与拱组成拱形桁架，减少主拱构件的弯矩，同时增强结构在沿拱跨度方向的整体性.

图11 拱脚基础形式Fig.11 Foundation arch types

洞口南侧跨越矿坑开口的5榀拱的拱脚由于受拱脚处岩石条件的限制，5榀拱的选形结果采用原方案的设计，其中深坑上方最南侧的3榀拱需向南侧倾斜放置，另2榀拱需向北侧倾斜放置，但总体上形成向南侧坑内倾斜的趋势，通过连系桁架将各榀拱联系在一起，提高拱受力的整体性.

各榀拱形桁架之间设置平面外连系桁架和连系梁，提高拱形桁架在平面外的稳定性.由于拱形曲面结构及拱形桁架总体上向坑内倾斜，产生倾覆力矩，连系桁架将各榀拱形桁架连成整体抵抗这一力矩，增加了结构的整体稳定性.

3.2 不同之处

3.2.1 洞口和拱脚位置的调整

根据ESO方法优化得到的拟合曲面和曲面上的控制点外壳线，相应地把径向的4榀主拱拱脚位置做了调整(图12)，这3处位置的径向拱对中间洞口起着三足鼎立的作用，两两近似120°的夹角，把整个壳体曲面分成西北、东北、南侧3部分，使剩下的3组环向拱能够相对独立地承担各自区域的竖向荷载作用，连系桁架最终把3部分形成统一的整体承担水平方向荷载的作用.

图12 拱脚位置变化Fig.12 Change of arches supporting location

楼面中间大约60 m直径的不规则开洞削弱了整体的完整性，主要由图12中三角形阴影区域的各榀拱和连系桁架发挥这一作用，其斜腹杆协调各榀桁架的变形产生轴力，并将轴力传递到连系桁架的上弦杆及梁板，最终通过锚杆传递到岩石.

3.2.2 拱形式和数量的调整

比较图3和图9两种选形方案可以发现，拱形式和数量的不同主要存在于B组拱和C组拱，各组分别减少了1榀拱，各组中的曲拱调整为直拱，直拱的受力性能较曲拱优越，对拱结构产生的扭矩作用小(图13)，而且减小了对中间洞口的挤压作用，从而能够削弱主体结构向坑内倾斜的趋势，提高了主体结构的整体稳定性.拱数量的减少主要考虑了B组拱和C组拱坑壁处的连系桁架可以锚固到岩石上，主体结构在静力作用下的位移和变形能够满足规范的要求，同时能够减少结构的用钢量和造价.

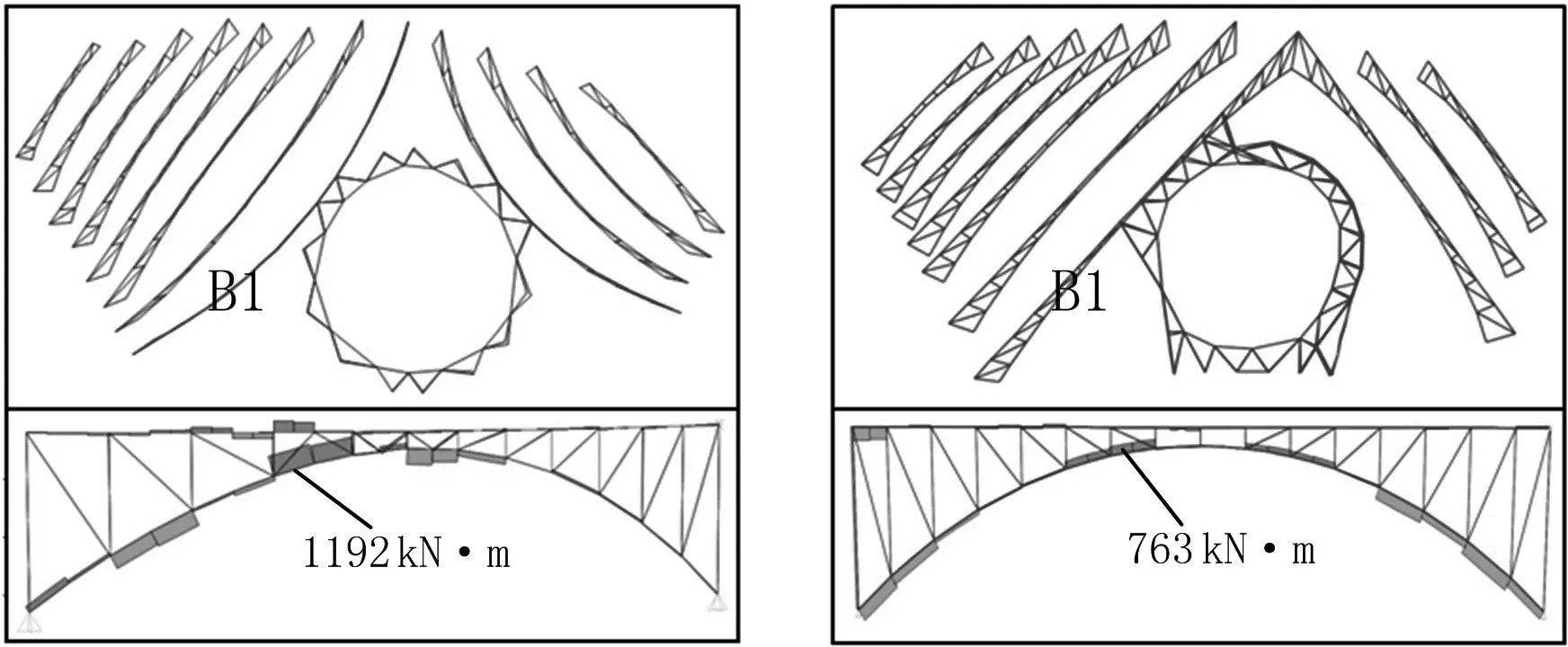
(a)原设计B1拱扭矩 (b) 现设计B1拱扭矩图13 两种方案的拱形式和数量比较Fig.13 Comparison of arch forms and quantities

3.2.3 静力荷载作用下的内力和变形

在静力荷载作用下，利用SAP2000有限元软件的自动优化设计功能，定义一组钢管截面为800～2 400 mm,壁厚为10～80 mm的自动截面选择列表，楼板采用200 mm厚的壳单元和C30的混凝土，对整体模型进行优化设计，使构件尺寸初步满足静力计算的要求，分析得到在各种工况下的内力和变形，分析结果如图14和表2,表3所示.

表2 整体模型在各种工况下的位移

Tab.2 Displacement of the model for various conditions

方案 位移/mm1.0D1.0L1.0D+1.0L1.2D+1.4L现设计(Ux)max484.955466(Uy)max49.56.34456(Uz)max-221-36.4-260-312原设计(Ux)max355.24045(Uy)max-20.85.6-28-31.5(Uz)max-156-23.4-182-210

注：D代表恒荷载，L代表活荷载；1.0,1.2和1.4是荷载分项系数.

(a)原设计变形图 (b) 现设计变形图

(c)原设计轴力图 (d) 现设计轴力图图14 整体模型在1.0D+1.0L下的变形和轴力图Fig.14 Deformation and axial force of the model in 1.0D+1.0L

方案荷载与内力区域1.0D1.0L1.0D+1.0L1.2D+1.4L现设计拱最大轴力/kNA1-72794-14054-85988-105825A2-72381-13730-86111-106080A3-74204-14464-88669-109295A4-69745-12493-82239-101186A5-63989-11176-75165-92434B1-70492-17367-87860-108906B2-63357-20625-83983-104905B3-38366-13616-51983-65103B4-47067-17788-64856-81385B5-56852-19662-76515-95750B6-39832-18571-58404-73799B7-42878-20538-63417-80208C1-25139-6946-32086-39892C2-32322-8042-40365-50047C3-48295-15890-64185-80200AB1-47481-9855-57336-70775BC1-12527-2563-15091-18621AC1-24698-6925-31624-39333AC2-38612-8013-46626-57554原设计拱最大轴力/kNA1-118120-16617-134738-165009A2-94336-13722-108058-132414A3-100002-15690-115693-141969A4-75218-11587-86707-106346A5-98820-13283-112103-137181B1-76691-13602-90293-111072B2-58704-14442-73147-90665B3-49804-14513-64335-80109B4-46201-15627-61829-77320B5-49962-19350-67838-85276B6-42266-18274-60541-76304B7-38313-15590-53903-67802B8-31177-11806-42983-53942C1-33913-5877-39790-48924C2-27907-6222-34130-42200C3-33243-11244-44488-55634C4-47045-17634-61289-76395AB1-36546-5710-42257-51850BC1-13345-2225-15571-19130AC1-29127-4867-33995-41767AC2-28767-5437-34205-42133

由分析结果可以看出，变形和内力主要是由恒荷载产生的，活载产生的变形和内力相对较小.结构总体上产生反向坑内变形的趋势，结构竖向位移和水平位移比原设计稍大，但都满足现行规范位移角限值1/250的要求[23]；主拱作为主要受力构件，各榀拱均承担着很大的轴力，表3中详细给出了各种工况下每榀拱上的最大轴力，详细比较现设计与原设计在1.0D+1.0L工况下的内力发现，现设计A组拱的总体内力低于原设计，B组拱、C组拱和4榀径向拱的总体内力都略低于原设计，而且各榀拱之间及每榀拱沿拱轴线的内力分布都相对比较均匀，说明了现设计选形结果比原设计具有一定的优越性.

3.2.4 结构材料利用率

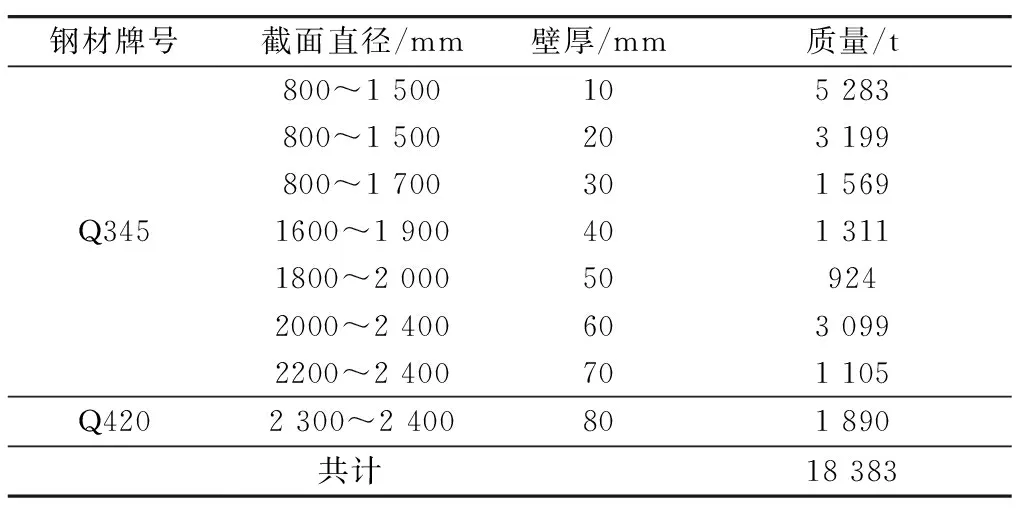
因圆形钢管截面和其他开口型钢截面相比，在构件的截面特性、受力性能和经济效益等方面都表现出了显著的优越性[24]，故本文初步选形优化以圆形钢管作为杆件.当截面尺寸小于2 400 mm时，采用Q345钢材；当截面尺寸为2 400 mm时，采用Q420钢材.因构件的应力水平与结构用钢量直接相关[25]，所以在进行优化设计时，将构件的应力比作为主要控制目标，考虑到结构的重要性及后期的商业利用，所有构件的控制应力比不大于0.8.现设计整体模型在静力荷载作用下的构件应力比及用钢量如图15和表4所示.

图15 构件的应力比Fig.15 Stress ratio of components

钢材牌号截面直径/mm壁厚/mm质量/tQ345800～1500105283800～1500203199800～17003015691600～19004013111800～2000509242000～24006030992200～2400701105Q4202300～2400801890共计18383

由原设计资料可知，原初步设计用钢量为41 176 t，显然，现设计的用钢量明显减少.由图15构件的应力比分布可知，结构的整体应力比接近比较合理的水平，从而达到了有效降低结构用钢量的目的；而结构的用钢量的大小直接与结构体系受力有关，因此，说明了基于ESO方法选形的结构受力体系对改善结构的整体受力起到了重要作用.

4 结论与建议

针对本文的研究，提出以下几点结论及建议：

1)本文主要利用ESO方法对一工程实例进行结构受力体系选形优化，并与原逆吊法选形结果进行对比研究，得出了2种方法在选形中存在的本质不同在于：逆吊法选形初期便确定了结构形态目标，选形是以曲面展开的，本着曲面—曲线—拱的选形路径；而ESO方法是基于不断删除低应力单元的准则，选形是以实体单元展开的，优化得到一个实体结构；最后本着实体—曲面—曲线—拱的选形路径通过一系列几何操作得到钢结构拱支承受力体系.

2)两种方法选形最后得到的曲面具有相似性，验证了两种选形方法的正确性及有效性.

3)根据本文分析结果，ESO方法选形结果比逆吊法选形结果具有优越性.ESO方法选形结果满足静力荷载作用下的内力和变形要求，具有一定的安全性；而且，在一定程度上降低了工程造价，达到了优化设计的目的.

4)就本文采用的钢结构拱支承受力体系，连系桁架和板面钢梁极大地改善了结构的整体刚度，减小了结构的变形，并形成了结构的抗侧力体系.

5)大跨空间结构受力复杂，工程造价高，利用优化分析的方法对结构受力体系进行选形是一个势在必行的发展趋势.因此，在选取优化方法时，需要综合考虑工程的实际情况，选取最适宜的选形方法以确保所求结果的可靠性与安全性.

[1] 王俊,赵基达,蓝天，等.大跨度空间结构发展历程与展望[J].建筑科学,2013,29(11):2-10.

WANG Jun，ZHAO Jida，LAN Tian,etal.Development process and future prospect of large-span spatial structures[J].Building Science，2013，29(11)：2-10.(In Chinese)

[2] BLETZINGER K U，RAMM E.Form finding of shells by structural optimization [J].Engineering with Computers，1993，9(1)：27-35.

[3] 张晋芳,赵人达.基于层次分析法的转换层结构选型[J].四川建筑科学研究,2009,35(1):51-54.

ZHANG Jinfang，ZHAO Renda.Selection of transfer floor structural types based on AHP[J].Sichuan Building Science，2009,35(1):51-54.(In Chinese)

[4] 杨海军,张爱林.基于Von Mises应力的预应力钢结构拓扑优化设计[J].北京工业大学学报,2010,36(4):475-481.

YANG Haijun，ZHANG Ailin.Topology optimization design of prestressed steel structures based on Von Mises stress[J].Journal of Beijing University of Technology，2010,36(4):475-481.(In Chinese)

[5] 王磊,杨彬,张其林.非均匀有理B样条曲面形状优化方法[J].湖南大学学报:自然科学版,2012，39(7):14-19.

WANG Lei，YANG Bin，ZHANG Qilin.Shape optimization of non-uniform rational B-spline surface [J].Journal of Hunan University：Natural Sciences，2012,39(7):14-19.(In Chinese)

[6] 谢亿民,左志豪,吕俊超.利用双向渐进结构优化算法进行建筑设计[J].时代建筑，2014(5)：20-25.

XIE Yimin，ZUO Zhihao，LV Junchao.Architectural design through bidirectional evolutionary structural optimization[J].Time Architecture，2014(5)：20-25.(In Chinese)

[7] 阴书玉,薄瑞峰,闫帅印,等.基于ESO算法的深孔机床多工况拓扑优化[J].制造技术与机床,2014(8):69-73.

YIN Shuyu，BO Ruifeng，YAN Shuaiyin，etal.Topology optimization under multiple loads for deep hole machine based on ESO algorithm [J].Manufacturing Technology & Machine Tool，2014(8):69-73.(In Chinese)

[8] 梅季魁,刘德明,姚亚雄.大跨建筑结构构思与结构选形[M].北京:中国建筑工业出版社,2003：1-60.

MEI Jikui，LIU Deming，YAO Yaxiong.The structural conception and form of large-span structures[M].Beijing：China Building Industry Press，2003：1-60.(In Chinese)

[9] 王光远,吕大刚,张世海.论结构选形的若干问题[J].哈尔滨建筑大学学报,2000,33(1):1-7.

WANG Guangyuan，LV Dagang，ZHANG Shihai.On some key problems for choice of structural styles[J].Journal of Harbin University of Civil Engineering and Architecture，2000，33(1)：1-7.(In Chinese)

[10]MEEK J L，XIA Xiaoyan.Computer shape finding of form structures [J].International Journal of Space Structures，1999，14(1)：35-55.

[11]武岳,李清明,沈世钊.基于逆吊实验原理的空间结构形态数值创建方法[J].建筑结构学报,2014,35(4):41-48.

WU Yue，LI Qingming，SHEN Shizhao.Computational morphogenesis method for space structures based on principle of inverse hanging experiment [J].Journal of Building Structures，2014，35(4)：41-48.(In Chinese)

[12]BAGNERIS M，MOTRO R，MAURIN B,etal. Structural morphology issues in conceptual design of double curved systems [J].International Journal of Space Structures,2008,23(2) ：79-87.

[13]LIU Min，XING Min，YANG Qingshan,etal.Computational morphogenesis of free from shell structures by optimization [J].Procedia Engineering，2012，31(1)：608-612.

[14]SEVILLA R，FERNNDEZ-MÉNDEZ S，HUERTA A.NURBS-enhanced finite element method [J].Archives of Computational Methods in Engineering，2008，76(1):56-83.

[15]XIE Y M，STEVEN G P.A simple evolutionary procedure for structural optimization [J].Computers & structures，1993，49(5)：885-896.

[16]CHU D N，XIE Y M，Hira A,etal. Evolutionary structural optimization for problems with stiffness constraint [J].Finite Elements in Analysis and Design，1996，21(4):239-251.

[17]LIU Xia，YI Weijian，LI Qiusheng，etal. Genetic evolutionary structural optimization [J].Journal of Constructional Steel Research，2008，64(3):305-311.

[18]张鹄志,刘霞,易伟建,等.复杂应力构件多荷载工况下的配筋优化[J].湖南大学学报:自然科学版,2014,41(9):42-47.

ZHANG Huzhi，LIU Xia，YI Weijian，etal. Reinforcement layout optimization of members under complex stress states and multiple loading cases[J].Journal of Hunan University：Natural Sciences，2014,41(9):42-47.(In Chinese)

[19]谢亿民,黄晓东,左志豪,等.渐进结构优化法(ESO)和双向渐进结构优化法(BESO)的近期发展[J].力学进展,2011,41(4):462-471.

XIE Yimin，HUANG Xiaodong，ZUO Zhihao，etal.Recent developments of evolutionary structural optimization (ESO) and bidirectional evolutionary structural optimization (BESO) methods [J].Advances in Mechanics，2011,41(4):462-471.(In Chinese)

[20]OHMORI H，FUTAI H，LIJIMA T,etal. Application of computational morphogenesis to structural design [J].Proceedings of Frontiers of Computational Sciences Symposium，2005，10 (11/13)：45-52.

[21]周健,张耀康,汪大绥,等.跨越100 m深坑——跨度达180 m的长沙冰雪世界主体拱形结构选形[EB/OL].[2014-10-14].http://chuansong.me/n/817401.

ZHOU Jian，ZHANG Yaokang，WANG Dasui，etal.The structural form design of “Ice and Snow World” cross a trench over 100 m deep and span of 180 m in Changsha city [EB/OL].[2014-10-14].http://chuansong.me/n/817401.(In Chinese)

[22]XIE Y M，STEVEN G P.Basic evolutionary structural optimization [M].Berlin:Springer London，1997:1-20.

[23]JGJ 7—2010 空间网格结构技术规程[S].北京：中国建筑工业出版社,2011：10-24.

JGJ 7-2010 Technical specification for space frame structures [S].Beijing：China Architecture & Building Press，2011:10-24.(In Chinese)

[24]关贤军,黄鼎业,尤建新.大跨预应力钢桁架优化设计和最优造价曲线研究[J].土木工程学报,2004，37(8):83-87.

GUAN Xianjun，HUANG Dingye，YOU Jianxin.Optimal design and cost-curve study for large-span prestressed steel trusses[J].China Civil Engineering Journal，2004,37(8):83-87.(In Chinese)

[25]吴耀华,吴文奇.钢管在结构工程中的应用与发展[J].钢结构,2005,20(2):45-49.

WU Yaohua，WU Wenqi.Application of steel tube to structural engineering and its development [J].Steel Construction，2005,20(2):45-49.(In Chinese)

Comparative Study on Optimization Methods for FormDesign of Large-span Spatial Structures

LIU Xia†，GUO Lijun，YI Weijian

(College of Civil Engineering，Hunan University，Changsha 410082，China)

In order to determine the optimal force system of a large-span spatial structure (LSSS)，based on the morphological knowledge and basic theory of ESO method，the three-dimensional solid model of an initial design domain was established by ANSYS software；and by taking the status of every unit as the design variables and the minimum volume as the objective function，the ESO method was then applied to the LSSS for structural force system optimization.To meet the architectural intent and the restrictions of special foundation conditions，the arch-bearing force system of steel structure was finally presented.Eventually，by comparing the static analysis results of the deformation and inner force for structural force systems determined by the ESO method and original inverse hanging method，the feasibility and availability of the ESO method was demonstrated.It is shown that the topology optimization methods are essential and necessary for optimizing structural force system of the LSSS.

large-span spatial structure; structural form optimization design; Evolutionary Structural Optimization(ESO); inverse hanging method; structural morphology;reliability analysis

1674-2974(2017)07-0007-09

10.16339/j.cnki.hdxbzkb.2017.07.002

2016-04-26

国家自然科学基金资助项目(51338004)，National Natural Science Foundation of China(51338004)

刘霞(1975—)，女，湖南常德人，湖南大学副教授†通讯联系人，E-mail:liuxiajy@tom.com

TU322

A