线路覆冰分层脱落动力响应的研究*

杜运兴，卢心龙，聂逸悠

(1.湖南大学 土木工程学院,湖南 长沙 410082;2.中国电建地产北京区域总部,北京 102300)

线路覆冰分层脱落动力响应的研究*

杜运兴1†，卢心龙1，聂逸悠2

(1.湖南大学 土木工程学院,湖南 长沙 410082;2.中国电建地产北京区域总部,北京 102300)

覆冰线路脱冰方式影响着整个线路的动力响应.利用数值试验方法建立了4塔5线有限元耦合模型，覆冰模拟采用附加冰单元法.研究了中跨中部导线外侧的两层覆冰同时发生脱落和两层覆冰在不同时刻相继发生不同厚度脱落时体系的动力响应.分析结果表明，两层覆冰在不同时刻相继发生脱落比覆冰在同一时刻一次性全部发生脱落引起的线路回弹高度、不平衡张力和跨中导线张力的最大值分别减小24%,17%和14%左右.当导线运动至最低点而第2层覆冰发生脱落时引起的线路回弹高度最大.无论两层覆冰脱落的时间间隔多长，线路脱冰后最终都具有相同的稳定振动状态.当最外层覆冰厚度占覆冰总厚度的3/5左右时，分层脱冰对线路体系的影响最小.对覆冰分层脱落的研究结果表明，以往采用覆冰一次性全部脱落假设得到的线路脱冰荷载取值偏保守，尚有可供优化的空间.

输电线路；脱冰；有限元；动力响应

线路覆冰时，冰的重量会导致线路上的支持结构和连接金具竖向负载增加、导线弧垂增大、同时导线张力变大.相邻导线不均匀覆冰或者不同期脱冰时，会在塔线连接处产生张力差，覆冰的脱落会导致导线向上跳跃引起相间短路，对铁塔产生较强的动力冲击作用.Morgan等[1]通过释放固定集中荷载的方式来模拟覆冰线路的脱冰过程，获得了各工况下导线的跳跃高度并推导了脱冰跳跃高度的近似计算公式；Fekr等[2]采用数值模拟的方法建立了输电线路数值模型，模拟了跨度、高差、覆冰厚度等参数对脱冰线路的影响；Kalman等[3]采用有限单元法定义了覆冰的破坏准则，使用脉冲荷载对机械除冰过程中线路脱冰的动力响应进行了模拟；Jamale-ddine等[4]建立了两跨简化缩尺的输电线路实验模型，采用集中荷载和均布荷载模拟各种脱冰工况，测量了各工况下导线的最大回弹高度、挂点张力、绝缘子位移和扭转角度；杨风利等[5]将四分裂导线简化为单根导线，分别研究了间隔棒、脱冰位置和数量、覆冰厚度、档距和高差等对脱冰导线动力响应抑制效果的影响程度；Laszlo等[6]开发了含间隔棒的各种分裂线路模型以代替以往常用的单一导线模型，考察了分裂导线的子导线发生脱冰后线路体系的动力行为，分析了应用间隔棒后脱冰线路的振幅、瞬态张力、最大跳跃高度和索张力的变化规律；沈国辉[7-8]和王昕[9]等人对塔线体系中导、地线脱冰的现象进行了数值模拟分析，研究了单分裂导线在各种不同覆冰和脱冰组合工况下的不平衡张力变化规律.

目前，各国学者在进行导线覆冰脱落的研究时，一般均假定附着在导线上的覆冰在某一时刻突然全部脱落，然而在大多数情况下导线外表面的冰并非在某一时刻全部脱落，线路上的脱冰通常是从线路上的局部位置开始，即每隔一段时间都会有不同位置的冰从导线外表面脱落，直至导线外表面的覆冰全部从导线上脱落完毕.因而真实的脱冰方式对体系的影响有别于以上学者分析时的假设.本文以分层脱冰的方式来模拟局部脱冰，研究分层脱冰对体系的整体影响.

由于脱冰试验线路受场地条件的限制，且从较小的比例模型上获得的数据并不能直接应用于实际线路的设计，所以当前的研究都倾向于采用数值模拟方法进行.计算机技术的发展和有限元理论在各研究领域的广泛应用，使得利用非线性有限元法来模拟线路脱冰振动成为一种比较有效的手段，因此，本文选择采用数值实验的方法，通过搭建塔线体系的耦合模型和简化模型，对线路外表面覆冰分层脱落的现象进行了探讨和研究.

1 数值模拟方法

1.1 线路有限元模型

本文中有限元模型所使用的输电塔型号为5B-ZBC1酒杯型塔，如图1所示，具体尺寸参照文献[10].输电塔架采用梁单元按空间刚架建模，考虑到导(地)线具有一定的抗扭刚度并承受一定扭矩，因而导(地)线采用忽略剪切变形的梁单元模拟，针对导(地)线抗拉不抗压的特性，利用MSC.Marc中的亚弹性材料来定义它的拉压方向的应力应变关系曲线(图2).当应变ε大于0时，弹性模量E取导(地)线实际的弹性模量；应变ε小于0时，弹性模量E取为0.导线和塔架之间连接使用的绝缘子串，采用Marc中的刚性连接来模拟(图3).文中模型使用的导(地)线具体参数如表1所示.

图1 5B-ZBC1塔Fig.1 5B-ZBC1 tower

图2 定义的应力应变曲线Fig.2 The stress strain curve defined in software

图3 绝缘子两端连接示意图Fig.3 Diagram of ends connection of insulators

型号弹性模量/GPa直径/mm单位长度质量/(kg·m-1)计算拉断力/kN导线 LGJ-400/356526.821.349103.9地线 JLB40-15010915.750.696790.62

1.2 输电线路找形分析和应力施加

架空线路是柔索结构，不能承受压力、弯矩和剪力，主要靠抗拉性能来承受外部荷载，会随着外力的变化而不断改变几何形态，具有极强的几何非线性.输电线路找形分析就是确定输电导线在自重作用下的平衡位置形态和相应的应力分布，它是进行输电线路动力分析的前提，其结果的准确程度直接影响后续动力分析的可靠性.本文采用文献[11]介绍的输电线路找形分析方法.为了证明该方法的适用性，采用一个简单的算例进行验证：建立一跨440 m的等高悬点架空导线，导线型号为LGJ-400/35，垂跨比为3.4%，按照文献[11]所述方法建立有限元模型，将其划分为220个单元.导线在自重作用下各个节点的弧垂和应力值如表2所示.由表2可知，二者误差较小，可以满足要求.

表2 有限元解和理论解对比

注:误差=(本文解/理论解-1)×100%.

1.3 阻尼

众所周知，线路在振动过程中会受到空气阻尼的影响，但这一影响在数值模拟中很难予以准确考虑.本文为简化计算，采用瑞利阻尼模型，即

C=αM+βK

(1)

式中:C,M,K分别为阻尼、质量和刚度矩阵；α和β为瑞利阻尼系数.对于输电塔通常取阻尼比为2%，覆冰导线取10%.一般而言β通常很小，为简化计算近似取0[12].

1.4 覆冰及脱冰荷载

假设冰均匀附着于导(地)线外表面，线路外侧的覆冰采用基于欧拉伯努利梁理论的闭合截面梁单元模拟，覆冰单元采用与导(地)线共节点的方式建立，如图4所示.进行线路自重找形分析时，冰单元处于“杀死”状态，自重阶段找形完成后“激活”冰单元并施加等效覆冰荷载进行自重和覆冰状态下的找形分析.等效覆冰荷载采用式(2)计算，进行脱冰的动力分析时，将外侧的覆冰单元移除即可.

图4 导线单元和覆冰单元Fig.4 Cable element and ice element in FEM simulation

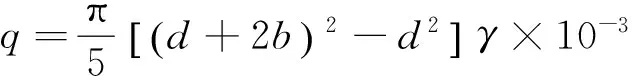
(2)

式中:q为单位长度上的覆冰荷载(N/m)；d为导线的直径(mm)；b为覆冰厚度(mm)；γ为覆冰重度(kN/m3)，取8.82 kN/m3.

2 线路脱冰模拟方法准确性验证

为验证本文采用附加冰单元法进行线路脱冰模拟的准确性，取以往的脱冰试验结果进行对比分析.线路脱冰的实测资料较少，而Jamaleddine等[4]于1996年在人工气候实验室内模拟覆冰脱落测得的数据记录全面，实验装置和过程描述详细，易于建立模型进行对比分析.该试验的简化模型如图5所示，模型由两跨档距为3.322 m的钢线组成，弧垂为0.196 m，初始拉力为6.603 N，试验钢线由直径为1.78 mm的不锈钢圆形截面绞接组成，用7根绞线绞织成直径为4.66 mm的线路，其单位长度质量为0.0926 kg/m.试验采用悬挂质量块的方式模拟覆冰，模拟的覆冰厚度为9.52 mm，脱冰工况为一档线路全部脱冰.

图5 试验模型Fig.5 Experiment model

在有限元软件中按照试验尺寸建立模型，每档划分100个单元进行脱冰分析.脱冰档跨中线路位移时程曲线的有限元和模型试验结果对比如图6所示(以覆冰平衡状态时的位置为零点).由于数值模型和试验模型的覆冰荷载施加方式不同，以及实际线路的阻尼也很难准确模拟，所以从图6中可以看出数值模型的峰值出现时间稍微滞后于试验模型，但二者的峰值数据均比较吻合，这表明本文采用附加冰单元法用于模拟脱冰没有问题.

图6 试验结果和数值模拟结果对比Fig.6 Results comparison of test and numerical simulation

3 典型输电线路覆冰分层脱落动力响应分析

输电线路表面的气候冰，在环境因素的影响下会逐渐从线路表面剥离，这一过程持续的时间因周围环境的不同而改变.目前，在关于线路覆冰脱落的研究中均假定覆冰均匀分布于线路外表面，且突然一次性全部脱落.本文在假设覆冰均匀分布于线路外表面的同时，进一步假定线路外表面的覆冰分为两层，这两层覆冰的脱落存在时间间隔Δt.为了探讨Δt的变化对覆冰线路结构动力响应的影响，本文首先建立了一个不包含输电塔的3跨等高悬点的简化模型，模型档距为440 m，垂跨比为3.4%，如图7所示.该模型两层覆冰总厚度为30 mm(15 mm+15 mm)，脱冰只发生于中跨.当中跨只发生最外层覆冰脱落时，脱冰跨跨中的竖向位移时程曲线如图8上半部分所示；当最外层覆冰在t1=2.0 s发生脱落后，第2层覆冰在不同的时刻t2发生脱落时，相对应的脱冰跨跨中的最大回弹高度统计如图8下半部分所示.

图7 简化模型Fig.7 Simplified model

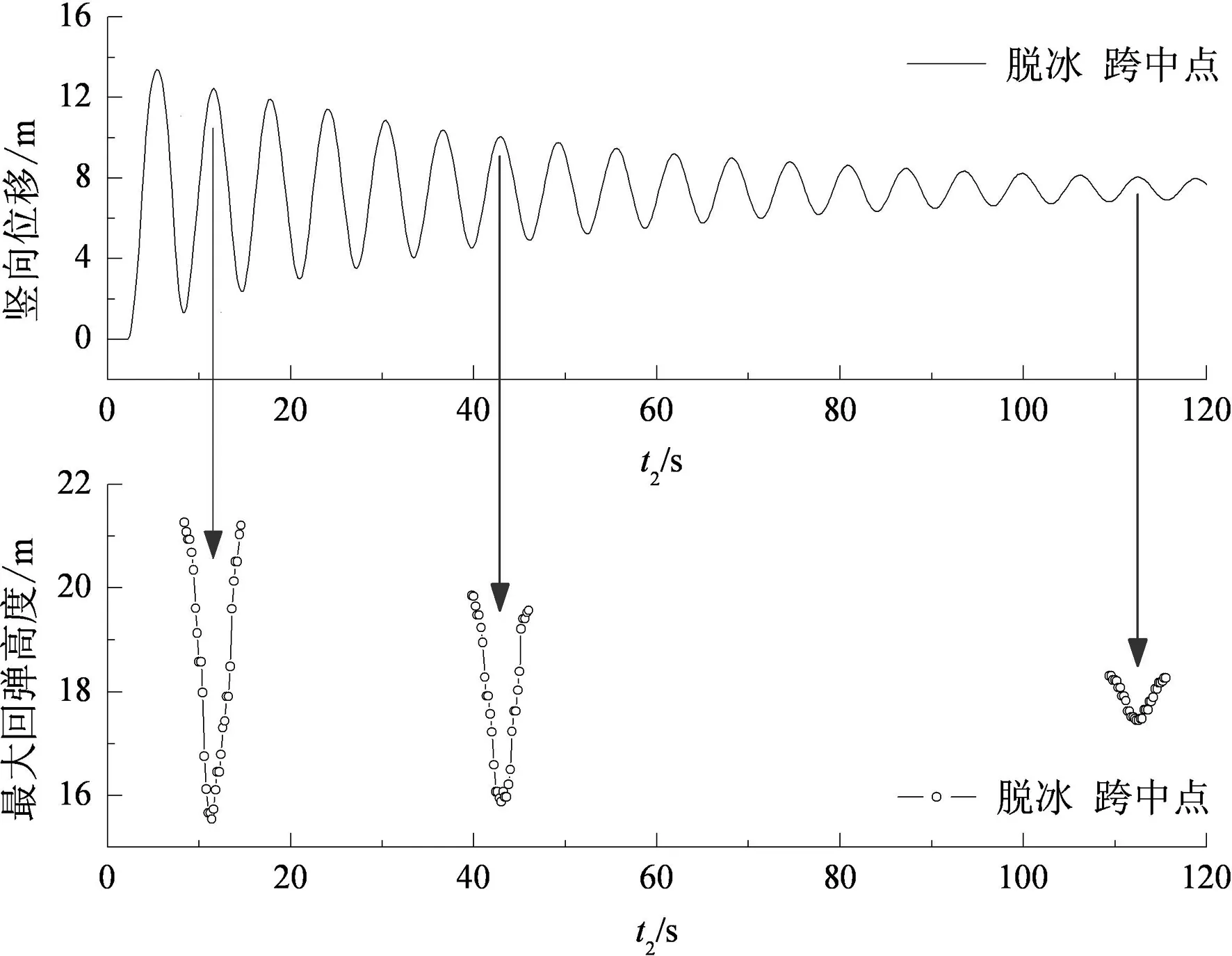
图8 回弹高度与Δt关系图Fig.8 The relationship of rebound height and Δt

从图8可以看出，当第2层覆冰发生脱落的时刻t2发生在脱冰跨导线运动至最低点时，脱冰跨中点的导线回弹高度最大；相反跨中导线运动至最高点发生第2层脱冰时，回弹高度最小.因此，当把第2层覆冰发生在图8上半部分跨中位移时程曲线的峰谷时刻的最大回弹高度连接起来即可得到一条随着时间间隔Δt变化的覆冰分层脱落产生的最大回弹高度上限曲线.为获得这一曲线，本文建立了包含输电塔在内的5跨输电塔线有限元模型(图9)，档距为440mm，垂跨比为3.4%.该模型中导(地)线覆冰均为30mm(15mm+15mm)，脱冰只发生在第2跨的中相导线，档距为440m，导(地)线处绝缘子串长为4.8m(0.6m).最外层15mm的覆冰在t1=2.0s(前2s为静力找形分析)时发生脱落，第2层覆冰在t2时刻(图10中标注的t2时刻)发生脱落，得到的结果如表3和图11—图15所示(图中所示的各变量点位置均位于跨中位置).

图9 塔线体系模型图Fig.9 Transmission tower-line system

图10 t2时刻位置Fig.10 Location of t2

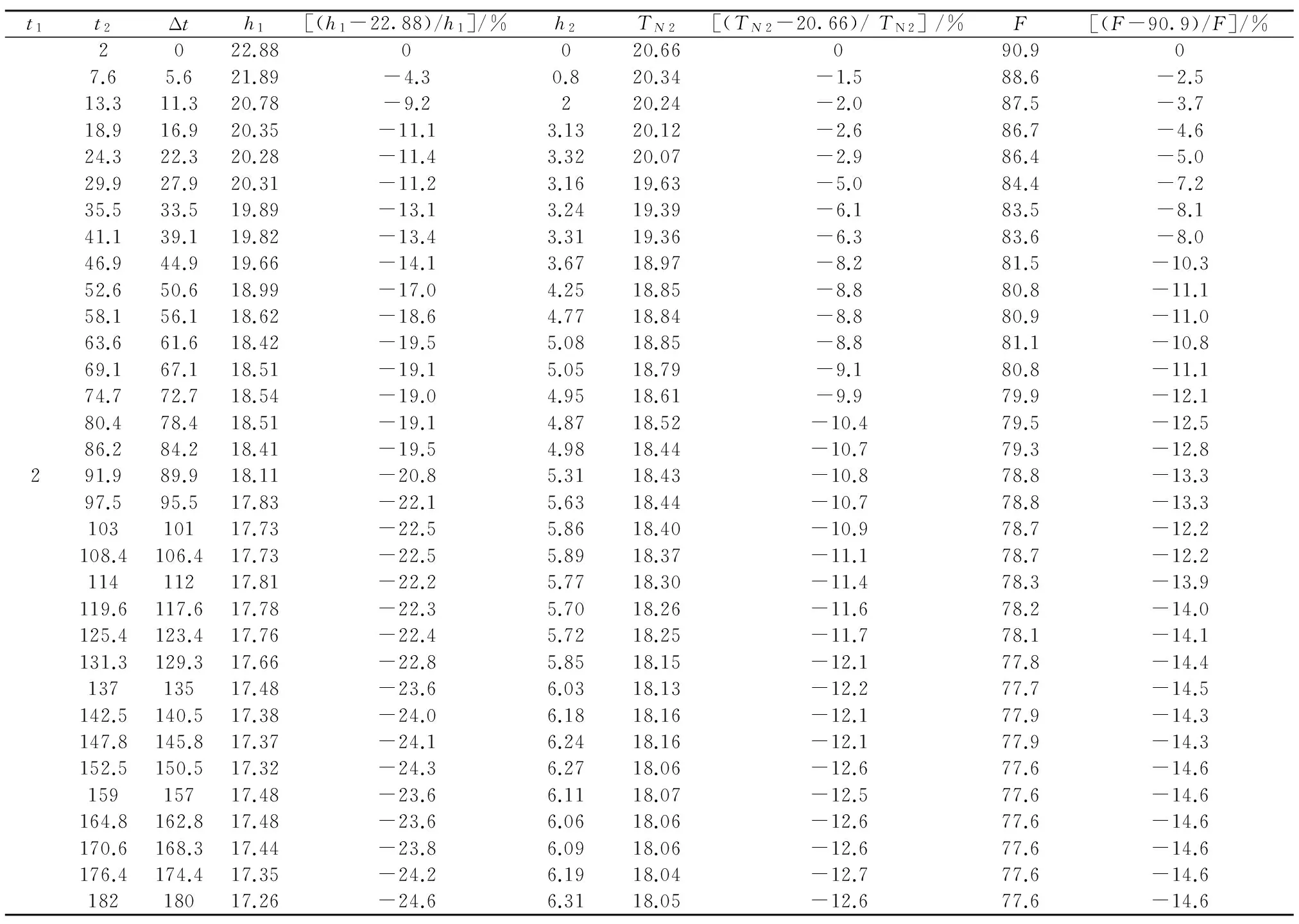
t1t2Δth1[(h1-22.88)/h1]/%h2TN2[(TN2-20.66)/TN2]/%F[(F-90.9)/F]/%2022.880020.66090.907.65.621.89-4.30.820.34-1.588.6-2.513.311.320.78-9.2220.24-2.087.5-3.718.916.920.35-11.13.1320.12-2.686.7-4.624.322.320.28-11.43.3220.07-2.986.4-5.029.927.920.31-11.23.1619.63-5.084.4-7.235.533.519.89-13.13.2419.39-6.183.5-8.141.139.119.82-13.43.3119.36-6.383.6-8.046.944.919.66-14.13.6718.97-8.281.5-10.352.650.618.99-17.04.2518.85-8.880.8-11.158.156.118.62-18.64.7718.84-8.880.9-11.063.661.618.42-19.55.0818.85-8.881.1-10.869.167.118.51-19.15.0518.79-9.180.8-11.174.772.718.54-19.04.9518.61-9.979.9-12.180.478.418.51-19.14.8718.52-10.479.5-12.586.284.218.41-19.54.9818.44-10.779.3-12.8291.989.918.11-20.85.3118.43-10.878.8-13.397.595.517.83-22.15.6318.44-10.778.8-13.310310117.73-22.55.8618.40-10.978.7-12.2108.4106.417.73-22.55.8918.37-11.178.7-12.211411217.81-22.25.7718.30-11.478.3-13.9119.6117.617.78-22.35.7018.26-11.678.2-14.0125.4123.417.76-22.45.7218.25-11.778.1-14.1131.3129.317.66-22.85.8518.15-12.177.8-14.413713517.48-23.66.0318.13-12.277.7-14.5142.5140.517.38-24.06.1818.16-12.177.9-14.3147.8145.817.37-24.16.2418.16-12.177.9-14.3152.5150.517.32-24.36.2718.06-12.677.6-14.615915717.48-23.66.1118.07-12.577.6-14.6164.8162.817.48-23.66.0618.06-12.677.6-14.6170.6168.317.44-23.86.0918.06-12.677.6-14.6176.4174.417.35-24.26.1918.04-12.777.6-14.618218017.26-24.66.3118.05-12.677.6-14.6

注：Δt=t2-t1为两层覆冰脱落的时间间隔，单位s；h1为第2层覆冰脱落后脱冰跨跨中最大回弹高度，单位m；h2为t2时刻脱冰跨跨中导线所处位置,相对于导线覆冰平衡时的位置而言，单位m;TN2为最大不平衡张力,图3中的N2节点处，单位kN；F为AS跨跨中最大导线张力，单位kN.

图11 t2与h1Fig.11 t2 and h1

图11中的曲线再次验证了前文简化模型所得结论：第2层覆冰发生脱落时(t2时刻)，线路所处位置越低(h2)，回弹高度h1越大(h2的波谷对应h1的波峰)，随着Δt的增大，回弹高度h1逐渐变小.若覆冰线路分两层脱落，则脱冰跨最大回弹高度随着两层覆冰的脱冰时间间隔Δt成指数函数变化，其函数拟合曲线为h1=1.78e-t2/4.37+4.89e-t2/59.79+17.06.当t2>180 s时，Δt对h1的影响趋向于稳定，h1基本维持在17 m左右，比最大值减小24%左右.由于本文建立的模型为理想对称模型，覆冰厚度均相同，相邻塔间无高差，且脱冰工况也是对称的，所以脱冰发生之前(t<2.0 s)线路的不平衡张力近似为0.当发生覆冰脱落后,不平衡张力开始出现(脱冰跨端部与绝缘子连接处，图3中2#塔的N2节点).

图12显示了脱冰线路中最大不平衡张力TN2随着Δt发生变化的情况，其规律符合指数函数TN2=2.91e-t2/52.25+17.95的分布.当t2>170 s后，线路最大不平衡张力稳定地维持在18 kN左右.当两层覆冰一次性全部脱落时，TN2最大为21 kN左右，比上述稳定值大了16.7%左右.

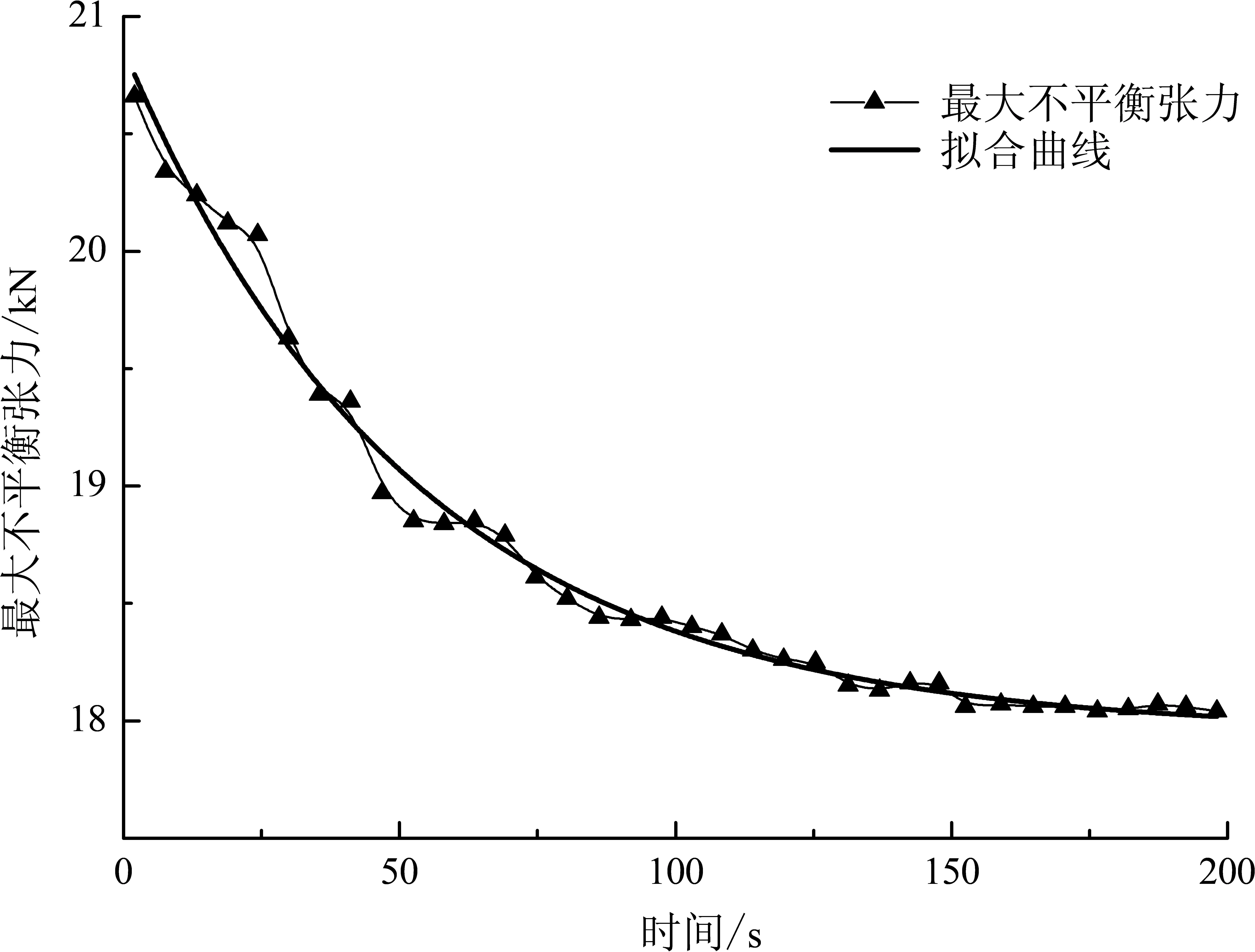
图12 TN2与t2Fig.12 TN2and t2

图13 N2点处不平衡张力TN2时程图Fig.13 Time history curve of unbalancete-nsionTN2 at location N2

图14 ISS跨竖向位移时程图Fig.14 Time history curve of vertical displacement of span ISS

图15 AS跨中张力F时程图Fig.15 Time history curve of tension F of span AS

图13-图15分别描述的是在t2=2.0,7.6,58.1,119.6和164.8 s时刻脱冰跨的不平衡张力TN2、回弹高度h1和AS跨中导线张力F的时程曲线.从图中可以看出，当t=2.0 s即第1层覆冰发生脱落时，TN2,h1和F第1次达到极值.当体系在振动过程中发生第2层覆冰的脱落时，TN2,h1和F均在很短的时间内第2次达到极值然后开始衰减且TN2,h1和F的第二极值均比第一极值要大(相关的增加百分比见表3)，Δt越小两个极值越接近，但最终结构体系均趋向于围绕同一水平的稳定状态上下振动.从上述分析可以得出结论：以往基于线路覆冰发生一次性全部脱落的假设进行的研究中，存在高估线路脱冰荷载的可能性.按照本文提出的覆冰分层脱落的构想进行的研究结果表明：覆冰发生分层脱落时脱冰跨最大回弹高度、最大不平衡张力及脱冰跨相邻的线路跨中最大张力分别比覆冰一次性全部脱落的假设减小了24%,17%和14%左右.

本文研究了覆冰线路分两层b1=b2脱落时脱冰线路的动力响应，实际线路脱冰过程中这两层覆冰可能并不相等，即b1≠b2.根据这一情况，本文设计了表4所示的6个工况进行了对比研究.6个工况中两层覆冰的时间间隔均取同一个固定值，即Δt=22.3 s，其中t1=2.0 s，t2=24.3 s，相关的计算结果如图16所示.从图16中可以看出,在6个设计工况中，h1,TN2和F的最大值均发生在工况6中，数值分别为22.9,20.7和90.9 kN；最小值出现在工况4中，数值分别为18.8,18.9和80.4 kN，比工况6分别减小了17.9%,8.7%和11.6%左右.随着最外层覆冰厚度占总覆冰厚度比重的增加，覆冰的分层脱落对输电线路体系造成的动力影响先增大后减小，当最外层覆冰厚度占总覆冰厚度的3/5左右时，脱冰对线路体系的动力影响最小.

表4 工况设置

图16 h1,TN2和F与b2关系图Fig.16 The relationship of h1,TN2,F and b2

4 结 论

本文基于输电线路覆冰分层脱落的假设，建立了4塔5线的输电线路模型，完成了静力找形分析，通过改变脱冰时间间隔Δt和两层覆冰的厚度比，探讨了输电线路覆冰分层脱落时结构的动力响应，并与基于线路覆冰一次性全部脱落假设得到的结果进行了对比分析并得到以下结论：

1)本文采用的线路找形方法与理论解相比误差较小，采用附加冰单元法模拟脱冰的结果与试验结果也很接近，可满足线路脱冰工况的动力响应分析.

2)基于覆冰分层脱落假设得到的脱冰线路回弹高度、不平衡张力和跨中线路张力值比基于覆冰一次性全部脱落假设的结果最大分别减小了24%，17%和14%左右.这表明以往按照一次性全部脱冰假设得到的结论进行线路设计偏于保守，对脱冰荷载的取值尚有优化空间.

3)当覆冰在线路运动至最低点发生脱落时，回弹高度最大.当最外层覆冰厚度占覆冰总厚度的3/5左右时，覆冰分层脱落对线路结构动力响应造成的影响最小.

[1] MORGAN V T,SWIFT D A.Jump height of overhead-line conductors after the sudden release of ice loads[C]//Proceedings of the Institutionof Electrical Engineers.England:IET Digital Library,1964,111(10):1736-1746.

[2] FEKR M R,MCCLURE G.Numerical modeling of the dynamic response of ice-shedding on electrical transmissionlines[J].Atmosphere Research,1998,46(1):1-11.

[3] KALMAN T,FARZANEH M,MCCLURE G.Numerical analysis of the dynamic effects of shock-load-induced ice shedding on overhead ground wires[J].Computers & Structure,2007,85(7):375-384.

[4] JAMALEDDINE A,BEAUCHEMIN R,ROUSSELET J,etal.Weigh-dropping simulation of ice-shedding effects on anoverhead transmissionlinemodel[C]//Proceedings of the 7th International Workshop on Atmospheric Icing of Struct-ures (IWAIS).Canada:Quebec University,1996:44-48.

[5] 杨风利,杨靖波,李正,等.覆冰输电线路脱冰跳跃及抑制方法研究[J].振动与冲击,2010,29(5):20-25.

YANG Fengli,YANG Jinbo,LI Zheng,etal.Ice-shedding and vibration suppression of a transmission line system[J].Journal of Vibration and Shock,2010,29(5):20-25.(In Chinese)

[6] LASZL O E,FARZANEH M.Vibrationof bundled conductors following ice shedding [J].IEEE Transactions on Power Delivery,2008,23(2):1097-1104.

[7] 沈国辉,袁光辉,邢月龙,等.导线覆冰脱落的数值模拟和参数分析[J].振动与冲击,2012,31(5):55-59.

SHEN Guohui,YUAN Guanghui,XING Yuelong,etal.Numerical simulation and parametric analysis of ice-shedding on conductors[J].Journal of Vibration and Shock,2012,31(5):55-59.(In Chinese)

[8] 沈国辉,袁光辉,孙炳楠,等.考虑脱冰速度效应的输电线路脱冰模拟[J].重庆大学学报,2010,33(9):132-138.

SHEN Guohui,YUAN Guanghui,SUN Bingnan，etal.Simulation of ice-shedding on transmission lines considering ice-shedding velocity effect[J].Journal of Chongqing University,2010,33(9):132-138.(In Chinese)

[9] 王昕,楼文娟.多跨输电线路脱冰动力响应研究[J].工程力学,2011,28(1):226-232.

WANG Xin,LOU Wenjuan.Dynamic response analysis of multi-span transmission line to ice-shedding shock[J].Engineering Mechanics,2011,28(1):226-232.(In Chinese)

[10]刘振亚.国家电网公司输变电工程典型设计500 kV输电线路[M].北京:中国电力出版社,2005:188-191.

LIU Zhenya.Power transmission project typical design of State gird corporation of China 500 kV transmission line branch[M].Beijing:China Electric Power Press,2005:188-191.(In Chinese)

[11]杜运兴,卢心龙.输电塔线体系风致覆冰脱落动力响应的研究[J].湖南大学学报:自然科学版,2015,42(11):88-94.

DU Yunxing,LU Xinlong.Research on dynamic response ofwind-induced ice-shedding of transmission tower-line system[J].Journal of Hunan University:Natural Sciences,2015,42(11):88-94. (In Chinese)

[12]胡位勇,严波,程皓月,等.输电塔线体系断线动力响应及杆塔破坏模拟研究[J].应用力学学报,2012,4(29):431-436.

HU Weiyong,YAN Bo,CHENG Haoyue,etal.Numericalinvestigation on dynamic response and failure oftransmission line and tower after wire breaking[J].Chinese Journal of Applied Mechanics,2012,4(29):431-436. (In Chinese)

Research on Dynamic Response of Ice Layer Shedding in Line System

DU Yunxing1†,LU Xinlong1,NIE Yiyou2

(1.College of Civil Engineering,Hunan University,Changsha 410082,China;2. Powerchina Real Estate Group Ltd Regional Headquarters in Beijing,Beijing 102300,China)

The ice-shedding way of iced conductors affects the dynamic response of transmission line system.In this paper，a finite element model of 4 towers and 5 spans is established by numerical method，and the ice is simulated by additional ice element method.The dynamic responses of the structure are analyzed when two-layer ice at mid-span of the middle conductor peels off at the same time and at different time with different thicknesses.The results show that the maximum rebound height，unbalanced tension and wire tension induced by one time ice-shedding are 24%，17% and 14% lower than those by ice-shedding at different time，respectively.The maximum rebound height of the system occurs when the second layer ice peels off and the conductor moves to the lowest position at the same time.The structure exhibits the same stable vibration state regardless of the interval time of the two ice layers shedding.When the thickness of outermost layer accounts for 3/5，the effect of ice layers shedding is minimal.The conclusions obtained by ice layer shedding research show that the values of ice-shedding load based on the assumption of one time ice-shedding are conservative，and there is some space for optimization.

transmission line system;ice-shedding;finite element;dynamic response

1674-2974(2017)07-0104-07

10.16339/j.cnki.hdxbzkb.2017.07.013

2016-04-15

国家自然科学基金资助项目(51261120374,51378199)，National Natural Science Foundation of China(51261120374,51378199)

杜运兴(1971—)，男，河南平顶山人，湖南大学副教授，博士†通讯联系人，E-mail:duyunxing@hnu.edu.cn

TM75

A