电子节气门的非奇异快速终端滑模控制*
2017-09-12孟志强喻文陈燕东高信严国鹏
孟志强,喻文,陈燕东,高信,严国鹏
(湖南大学 电气与信息工程学院,湖南 长沙 410082)
电子节气门的非奇异快速终端滑模控制*
孟志强,喻文†,陈燕东,高信,严国鹏
(湖南大学 电气与信息工程学院,湖南 长沙 410082)
为了提高汽车电子节气门开度控制的响应速度和精确度,研究与设计了一种非奇异快速终端滑模控制策略.建立了电子节气门控制系统的非线性数学模型;利用节气门阀片实际开度与期望开度的误差及误差的导数设计非奇异快速终端滑模面和终端吸引子,使用扩张状态观测器估计开度的一阶导数,设计了不存在奇异控制量且收敛快速的节气门非奇异快速终端滑模控制器,证明了这种控制器的李雅普若夫稳定性;对4种参考输入信号使用非奇异快速终端滑模控制和普通滑模控制在MATLAB/simulink 中进行了仿真.仿真结果表明,相比于普通滑模控制方法,非奇异快速终端滑模控制方法具有更短的调节时间和更小的跟踪误差,在4种参考输入信号的作用下,普通滑模控制器需要1 s甚至1.2 s的时间才可基本实现跟踪,且跟踪误差较大,而非奇异快速终端滑模控制器可确保电子节气门开度在0.1 s实现对参考信号的跟踪,且跟踪误差的绝对值小于0.2°,同时冲击扰动信号作用下的仿真结果表明非奇异快速终端滑模控制器具有较好的鲁棒性.
电子节气门;非奇异快速终端滑模控制;扩张状态观测器;李雅普诺夫稳定性
节气门是空气进入发动机的咽喉,在汽车发动机控制中起着举足轻重的作用.电子节气门具有严重的非线性(如复位弹簧的非线性、齿轮啮合间隙、库伦摩擦和粘滑摩擦等)、参数不确定性(如电路中电阻随温度上升而增大、设备老化、产品差异等)以及外部扰动(如气压变化等)和时滞等[1].因此,很难得到精确的电子节气门数学模型.为满足电子节气门开度响应速度快和精度高的要求,同时提高系统的鲁棒性,学者们一直致力于设计一种合适的控制律,如将神经网络控制[1]、PID控制[2]、模糊控制[3-4]、backstepping方法[5]、滑模控制[6-7]等方法引入电子节气门控制中,以提高节气门的控制精度和响应速度.
滑模控制可以很好地克服系统的不确定性,同时对外界扰动具有极强的鲁棒性[8-9].终端滑模 (Terminal Sliding Mode,TSM) 控制方法通过在滑模面中适当引入非线性函数,解决了系统无法在有限时间收敛至零的问题,但该方法在控制律中引入了状态量的负指数项[10].当系统状态量趋近于0时,该负指数项将导致控制律趋于无穷大,即产生了奇异问题,这在实际系统中是无法实现的.文献[11]以误差和误差的导数设计滑动超平面,提出了非奇异终端滑模 (Non-singular Terminal Sliding Mode,NTSM) 控制方法,该方法从数学角度直接避免了TSM的奇异问题,同时使得系统可以在有限时间内收敛.但是NTSM方法在远离平衡点处收敛速度过慢.为此,文献[12]改进并提出了非奇异快速终端滑模(Non-singular Fast Terminal Sliding Mode,NFTSM) 控制方法,该方法通过在滑动超平面引入状态量的高次项和设计带状态负指数的终端吸引子,保证了系统在远离平衡点处具有比NTSM控制更快的收敛速度.文献[13]将非奇异快速终端滑模控制用于汽车电子节气门控制,实现最少传感器的跟车控制.
为提高节气门开度的响应速度和精确度,提高系统的鲁棒性,本文以节气门阀片的实际开度与期望开度的误差及误差的导数来设计非奇异快速终端滑模面和终端吸引子,使用扩张状态观测器估计开度的一阶导数,设计了一种非奇异快速终端滑模控制律,采用李雅普诺夫稳定性理论分析了控制律的收敛性,最后在MATLAB/simulink中搭建仿真模型,仿真实验表明了该方法的可行性.
1 电子节气门的数学模型
电子节气门控制系统结构如图1所示[1],此控制系统由车载微控制器、斩波器和电子节气门体3大部分组成,以节气门开度θ为控制变量.
作为一个非线性系统,电子节气门体的非线性主要来自3个方面[3]:摩擦力、非线性复位弹簧和齿轮间隙.

图1 电子节气门控制系统结构图Fig.1 The structure diagram for an electronic throttle control system
节气门阀片在转动过程中存在的摩擦主要是粘滑摩擦和库伦摩擦.粘滑摩擦力矩正比于节气门阀片的转动速度,库伦摩擦力矩大小正比于库伦摩擦系数kstf.因此摩擦力矩TSS可表示为:
(1)
式中:θ为节气门开度;kslf为粘滑摩擦系数;kstf为库伦摩擦系数.
假设电子节气门复位弹簧的质量为零且弹性系数固定不变,则非线性复位弹簧的力矩Trsp可表示为:
Trsp=krsp(θ-θ0)+kpresgn(θ-θ0)
(2)
式中:krsp为复位弹簧弹性系数;kpre为复位弹簧预紧力矩;θ0为节气门“跛行回家”角度.
考虑到全新电子节气门齿轮间隙产生的非线性对系统影响较小,本文电子节气门控制系统建模时忽略齿轮间隙的非线性,在仿真阶段将齿轮间隙非线性与外界扰动一起作为有界扰动叠加到系统中.
在图1所示的控制系统中,对于斩波器部分有:
Ea=Kch×u
(3)
对于直流电机部分,根据基尔霍夫定律有:
(4)
(5)
Tm=Km×i(t)
(6)
式中:Kch为斩波器增益;u为斩波器控制输入电压;Ea为电机电枢电压;i(t)为电机电枢电流;Ra为电机电枢绕组电阻;La为电机电枢绕组电感;EV为电机反电动势;KV为电机反电动势常数;θm为电机旋转角度;Tm为电机输出转矩;Km为电机转矩常数.
以电机轴为参考点,根据牛顿第二定律,电机旋转角度θm的动力学方程为:
(7)
式中:Jm为电机转动惯量;bm为电机轴阻尼系数;Tl为电机负载转矩.
以节气门体阀片轴为参考点,根据牛顿第二定律,节气门体阀片旋转角度θ的动力学方程为:
(8)
式中:T为作用在节气门阀片轴上的转矩;J为节气门阀片转动惯量;θ为节气门阀片开度.
假定减速齿轮满足理想传动比关系且比例系数为N,则有:
(9)
由式(9)可得:
θm=N×θ
(10)
(11)
对式(10)分别求一阶导和二阶导可得:
(12)
(13)
(14)
通过整理式(1)~式(14)可得:
(Krsp(θ-θ0)+Kpresgn(θ-θ0))]
(15)
(16)
其中:
f(x)=a11(x1-θ0)+a12sgn(x1-θ0)+
a21x2+a22sgn(x2)+a23x2
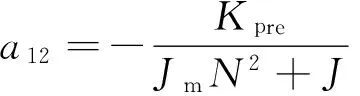
式中:d为有界扰动且满足|d|≤D.
2 控制器的设计
2.1 非奇异快速终端滑模控制器
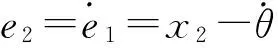
受文献[12]的启发,设计针对控制系统(16)的非奇异快速终端滑模面为:
(17)
式中:α∈R+;β∈R+;p,q,g,h均为正奇数,且满足1
p/q,sgn为符号函数.
设计趋近律为:
(18)
式中:φ∈R+;γ∈R+;m,n均为正奇数,且满足0 根据式(16),(17)和(18),设计非奇异快速终端滑模控制律为: |e2|2-p/qsgn(e2)+ (19) 因p,q,g,h满足1 p/q,使2-p/q>0,g/h-1>0,故式(19)不存在奇异现象. 2.2 滑模控制的收敛性分析 为了验证控制系统的收敛性,定义李雅普诺夫函数为: (20) 由李雅普诺夫稳定性原理可知,如果满足Ⅰ:选取的李雅普诺夫函数为具有连续一阶导数的正定函数V;Ⅱ:dV/dt为半负定且不恒为0,则系统在滑模面处为大范围渐近稳定. 对式(17)求导可得: (21) 对式(20)求导并将式(19)和(21)代入可得: -(φS2+γ|S|m/n+1)|e2|p/q-1 (22) 当系统状态运动到滑模面后,有S=0,因此由式(17)可得降阶方程为: (23) (24) 2.3 扩张状态观测器 控制律式(19)用到了电子节气门阀片开度的一阶导数.然而,在实际过程中可测量量仅为节气门阀片开度.因此,需要通过间接方法获取开度的一阶导数.文献[14]针对一类非线性系统设计一种具有抗干扰性的高增益扩张状态观测器,实现了对信号的n阶导数的观测.从文献的证明可以看出,观测误差的收敛速度与所选取的参数ξ有关,通过选取合适的参数,即可保证观测误差快速收敛,具体的证明过程详见文献[14].本文以节气门阀片的实际开度与状态观测器的观测值为误差,设计扩张状态观测器为: (25) 式中:a1,a2和a3均为正实数;ξ>0为摄动参数;1为对θ的估计值;2为对的估计值.通过选取合适的参数即可实现对的有效估计. (26) 为验证非奇异快速终端滑模控制策略的有效性,在MATLAB/Simulink环境下搭建了电子节气门控制仿真模型,系统整体仿真模型如图2所示,其中控制律模块为式(26),节气门数学模型模块为式(16),扩张状态观测器模块为式(25). 图2 电子节气门控制系统仿真结构图Fig.2 The simulation structure diagram for an electronic throttle control system 为了验证NFTSM控制律的效果,仿真实验使用普通滑模 (Sliding Mode,SM) 控制进行比对. 定义普通滑模面为: SS=e1+ce2 (27) 设计控制律为: (28) 电子节气门模型参数如表1所示,电子节气门仿真参数如表2所示.考虑到系统中存在齿轮间隙等未建模扰动,因此在节气门数学模型模块中加入一个最大值为5的高斯白噪声作为扰动. 所选取的节气门参考输入信号分别为:正弦信号、阶跃信号、三角波信号和近似阶梯信号. 表1 电子节气门模型参数表Tab.1 Electronic throttle valve mathematical model parameter 3.1 正弦信号跟踪响应性能分析 图3(a)和图3(b)分别为NFTSM控制器和SM控制器在幅值为60°的正弦信号作用下的跟踪波形和跟踪误差波形.从图3可以看出,两种滑模控制均能实现开度跟踪.NFTSM控制的电子节气门开度在0.1 s 就基本与参考信号一致,稳态误差小于0.1°,基本无超调;普通滑模控制的节气门开度需要近1 s时间才能实现跟踪,跟踪误差达到3°,且存在明显的振荡. 表2 电子节气门仿真参数表Tab.2 Electronic throttle valve simulation parameter (a)正弦信号跟踪曲线 (b)正弦信号跟踪误差曲线图3 正弦信号跟踪与跟踪误差曲线Fig.3 Tracking and tracking error curve of sine signal 3.2 阶跃信号跟踪响应性能分析 图4(a)和图4(b)分别为NFTSM控制器和SM控制器在幅值为60°的阶跃信号作用下的跟踪波形和跟踪误差波形.从图4可以看出,NFTSM控制的电子节气门和普通滑模控制的电子节气门在达到稳定状态时稳态误差均趋近于0.不同的是,NFTSM控制的节气门在0.1 s左右即可快速稳定至给定跟踪位置,而普通滑模控制的节气门需要大约1.5 s以后才能稳定至给定跟踪位置. (a)阶跃信号跟踪曲线 (b)阶跃信号跟踪误差曲线图4 阶跃信号跟踪与跟踪误差曲线Fig.4 Tracking and tracking error curve of step signal 3.3 三角波信号跟踪响应性能分析 图5(a)和图5(b)分别为NFTSM控制器和SM控制器在最大幅值为60°的三角波信号作用下的跟踪波形和跟踪误差波形.从图5 中可以看出,NFTSM控制的电子节气门不到0.1 s 即可与参考信号一致,在给定参考信号变化的过程中出现的最大误差的绝对值小于0.2°;普通滑模控制的电子节气门在给定参考信号处经过1 s后仍未能与参考信号保持一致,且在给定参考信号变化的过程中出现的最大误差超过3.5°. (a)三角波信号跟踪曲线 (b)三角波信号跟踪误差曲线图5 三角波信号跟踪与跟踪误差曲线Fig.5 Tracking and tracking error curve of triangle wave signal 3.4 近似阶梯信号跟踪响应性能分析 图6(a)和图6(b)分别为NFTSM控制器和SM控制器在最大幅值为60°的近似阶梯信号作用下的跟踪波形和跟踪误差波形.从图6中可以看出,NFTSM控制的电子节气门大约在经过0.1 s后能较地的跟踪给定参考信号且稳定后几乎无超调,调节过程中出现的最大跟踪误差的绝对值小于0.2°;而普通滑模控制的电子节气门在对给定参考信号跟踪过程中几乎一直处于调节状态,跟踪效果较差,最大跟踪误差的绝对值大于4°. (a)近似阶梯信号跟踪曲线 (b)近似阶梯信号跟踪误差曲线图6 近似阶梯信号跟踪与跟踪误差曲线Fig.6 Tracking and tracking error curve of sine signal 3.5 冲击扰动信号作用下的控制系统鲁棒性能分析 为验证系统的鲁棒性,4.5 s时,在节气门数学模型模块中分别加入幅值为30,50,70和90且持续时间为0.02 s的冲击扰动信号,用以模拟节气门体参数的变化和扰动影响. 以幅值为70的冲击信号为例,图7(a)和图7(b)分别为NFTSM控制器和SM控制器在幅值为60°的阶跃信号作用下的跟踪波形和跟踪误差波形.从图7中可以看出,NFTSM控制方法和SM控制方法均具有较好的鲁棒性,在冲击信号作用下,NFTSM控制方法出现的最大误差角度约为0.012 5°,SM控制方法出现的最大误差角度约为0.017°.其它幅值冲击信号作用下的角度误差见表3.结果表明NFTSM控制方法能使系统具有良好的鲁棒性. (a)4.5 s时施加幅值70的冲击扰动作用下, 阶跃信号跟踪曲线 (b)4.5 s时施加幅值70的冲击扰动信号作用下, 阶跃信号跟踪误差曲线图7 冲击扰动信号作用下的阶跃信号跟踪与 跟踪误差曲Fig.7 Tracking and tracking error curve of step signal under the impulsive disturbance signals 冲击扰动幅值NFTSMC最大误差/(°)SMC最大误差/(°)300.0058-0.0004500.00900.0060900.01500.0300 对电子节气门开度响应速度快和精确度高的要求,利用终端滑模控制的有限时间收敛和滑模控制强鲁棒性的特点,设计了基于电子节气门数学模型的非奇异快速终端滑模控制器,利用李雅普诺夫稳定性理论分析了控制律的收敛性.仿真实验结果表明,非奇异快速终端滑模控制器能确保节气门开度的良好跟踪,跟踪过程具有响应速度快、调节时间短和稳态误差小的特点,同时,非奇异快速终端滑模控制方法对节气门体参数的变化或扰动具有较强的鲁棒性,能够满足节气门的控制要求. [1] YUAN X,WANG Y,WU L,etal.Neural network based self-learning control strategy for electronic throttle valve[J].IEEE Transactions on Vehicular Technology,2010,59(8):3757-3765. [2] WANG H,YUAN X,WANG Y,etal.Harmony search algorithm-based fuzzy-PID controller for electronic throttle valve[J].Neural Computing and Applications,2013,22(2):329-336. [3] BAI R,LIU Y,WANG S.Fuzzy sliding-mode control of the electronic throttle system[C]//Proceeding of the 11th World Congress on Intelligent Control and Automation (WCICA).Shenyang,China:IEEE,2014:747-750. [4] CHEN L,RAN C.A fuzzy immune PID controller for electr-onic throttle[C]//Proceedings of the 2nd International Symposium on Computational Intelligence and Design.Changsha,China:IEEE,2009:72-75. [5] 陈虹,胡云峰,郭宏志,等.基于 backstepping 方法的电子节气门控制[J].控制理论与应用,2011,28(4):491-496. CHEN Hong,HU Yunfeng,GUO Hongzhi,etal.Control of electronic throttle based on backstepping approach[J].Control Theory & Applications,2011,28(4):491-496.(In Chinese) [6] PAN Y,OZGUNER U,DAGCI O H.Variable-structure cont-rol of Electronic throttle valve[J].IEEE Transactions on Industrial Electronics,2008,55(11):3899-3907. [7] 郑太雄,杨斌,李永福,等.车联网环境下电子节气门全局快速滑模控制[J].仪器仪表学报,2014,35(10):2356-2364. ZHENG Taixiong,YANG Bin,LI Yongfu,etal.Global fast sliding mode controller for electronic throttle valve under the environment of IoV[J].Chinese Journal of Scientific Instrument,2014,35(10):2356-2364.(In Chinese) [8]周华安,孟志强,王保田.光伏发电系统MPPT固定频率滑模控制[J].湖南大学学报:自然科学版,2015,42(10):97-101. ZHOU Huaan,MENG Zhiqiang,WANG Baotian.Fixed-frequency-sliding-mode controller used in photovoltaic system MPPT[J].Journal of Hunan University:Natural Sciences,2015,42(10):97-101.(In Chinese) [9] 黄守道,徐振宇,肖磊,等.基于滑模变结构的PMSM的直接转矩控制[J].湖南大学学报:自然科学版,2012,39(1):52-56. HUANG Shoudao,XU Zhenyu,XIAO Lei,etal.Direct torque control of PMSM based on sliding mode[J].Journal of Hunan University:Natural Sciences,2012,39(1):52-56.(In Chinese) [10]张袅娜.终端滑模控制理论及应用[M].北京:科学出版社,2011:2-5. ZHANG Niaona.Terminal sliding mode control theory and its application[M].Beijing:Science Press,2011:2-5.(In Chinese) [11]FENG Y,YU X,MAN Z.Non-singular terminal sliding mode control and its application for robot manipulators[C]//Proceedings of IEEE International Symposium on Circuits and Systems.Sydney,Australia:IEEE,2001:545-548. [12]李升波,李克强,王建强,等.非奇异快速的终端滑模控制方法[J].信息与控制,2009,38(1):1-8. LI Shengbo,LI Keqiang,WANG Jianqiang,etal.Nonsingular and fast terminal sliding mode control method[J].Information & Control,2009,38(1):1-8.(In Chinese) [13]李升波,李克强,王建强,等.非奇异快速的终端滑模控制方法及其跟车控制应用[J].控制理论与应用,2010,27(5):543-550. LI Shengbo,LI Keqiang,WANG Jiangqiang,etal.Nonsingular fast terminal-sliding-mode control method and its application on vehicular following system[J].Control Theory & Applications,2010,27(5):543-550.(In Chinese) [14]王新华,陈增强,袁著祉.基于扩张观测器的非线性不确定系统输出跟踪[J].控制与决策,2004,19(10):1113-1116. WANG Xinhua,CHEN Zengqiang,YUAN Zhuzhi.Output tracking based on extended observer for nonlinear uncertain systems[J].Control & Decision,2004,19(10):1113-1116.(In Chinese) A Non-singular Fast Terminal Sliding Mode Control for Electronic Throttle Valve MENG Zhiqiang,YU Wen†,CHEN Yandong,GAO Xin,YAN Guopeng (College of Electrical and Information Engineering,Hunan University,Changsha 410082,China) In order to improve the response speed and accuracy of automotive electronic throttle valve opening control,a Non-singular Fast Terminal Sliding Mode (NFTSM) control strategy was designed.Firstly,the non-linear mathematical model was obtained by analyzing the nonlinear and disturbance of the electronic throttle valve control system.Secondly,a NFTSM surface and a terminal attractor were constructed by using the error between electronic throttle opening and the desired opening and the derivative of the error,at the same time,an extended state observer was applied to estimate the first order derivative of the opening degree.Meanwhile,a NFTSM controller with no singular control and fast convergence was designed,which verified the stability of the controller by using Lyapunov's stableness theory.A number of simulations were conducted to test and verify the performances of the NFTSM control method and conventional sliding mode control method in MATLAB/simulink by using sine signal,step signal,triangle wave signal and approximate stair-step signal as the input signals respectively.The simulation results show that the NFTSM control method has shorter settling time and smaller tracking error compared with the conventional sliding mode control method.NFTSM controller can keep the electronic throttle opening consistent with reference signals in 0.1 s and has steady-state error less than 0.2°,while the conventional sliding mode controller needs more than 1 s and has large tracking error.In addition,the simulation results of the system under the impulsive disturbance signal show that the NFTSM controller has excellent robustness. electronic throttle valve;non-singular fast terminal sliding mode (NFTSM);extended state observer;Lyapunov's stableness theory 1674-2474(2017)08-0070-07 10.16339/j.cnki.hdxbzkb.2017.08.011 2016-12-09 国家自然科学基金资助项目(51577056),National Natural Science Foundation of China(51577056) 孟志强(1964—),男,湖南益阳人,湖南大学教授,博士生导师 †通讯联系人,E-mail: yw0214@hnu.edu.cn TP273 A

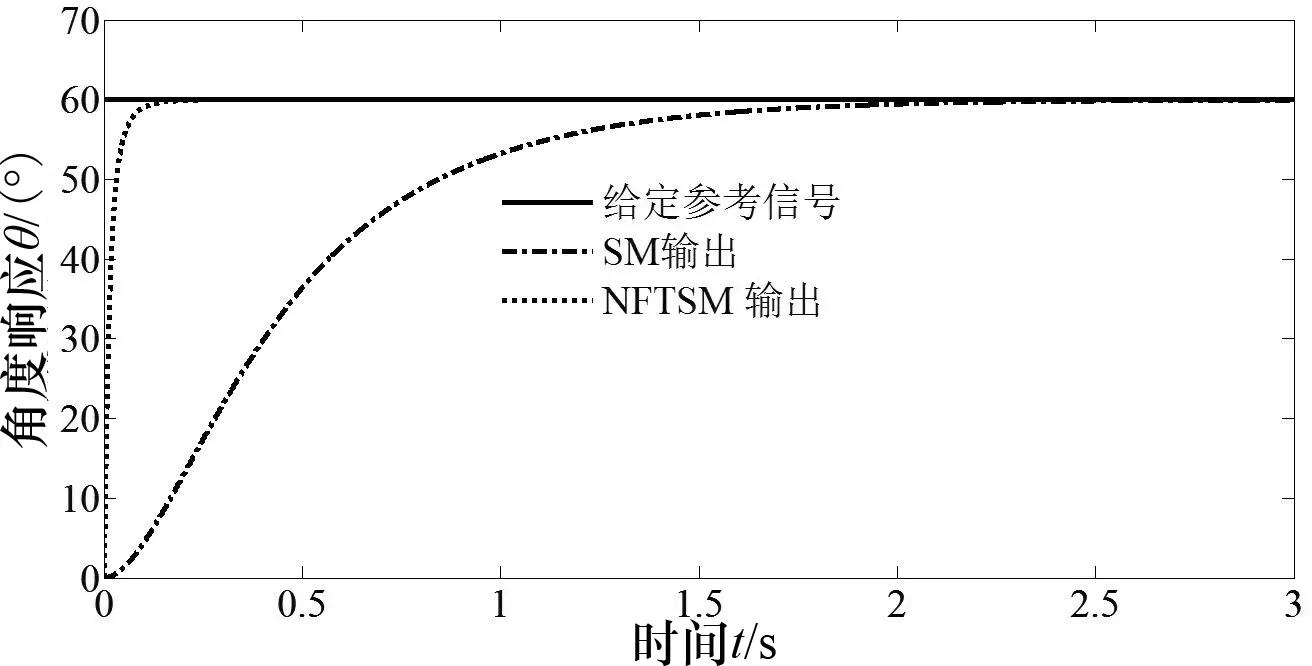
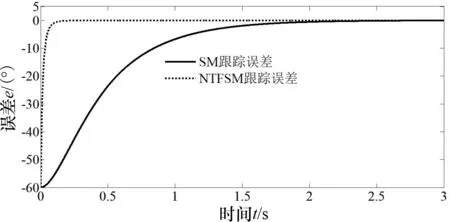
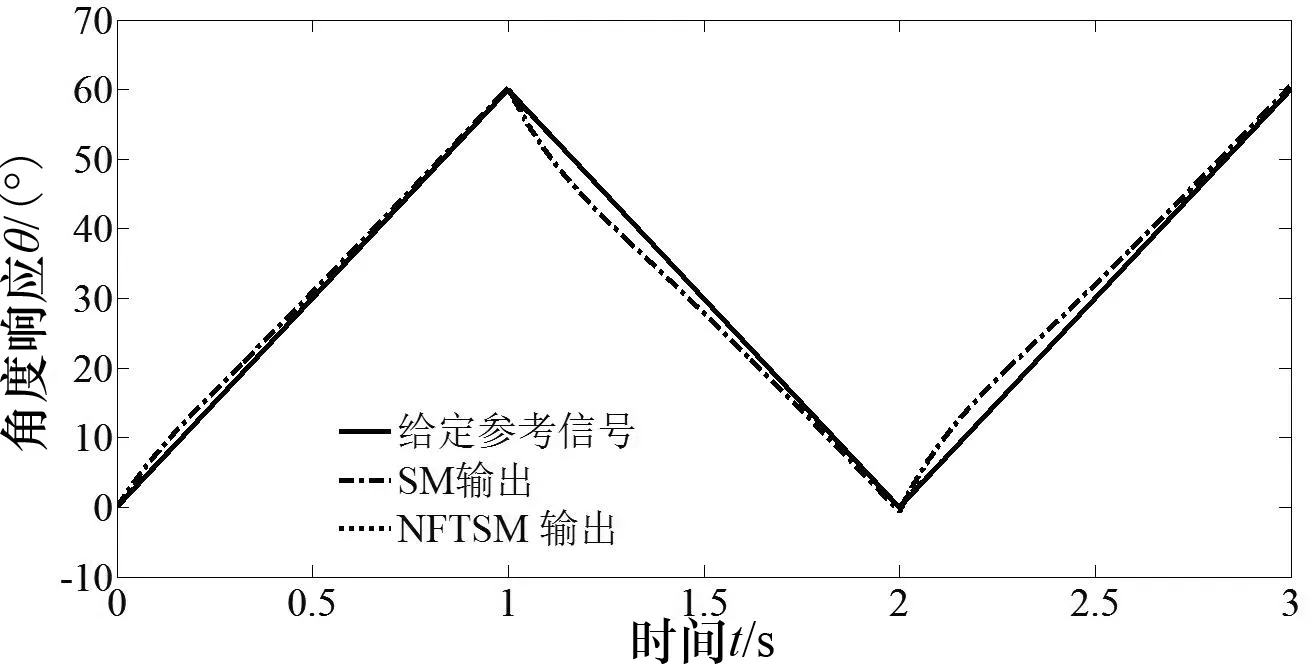
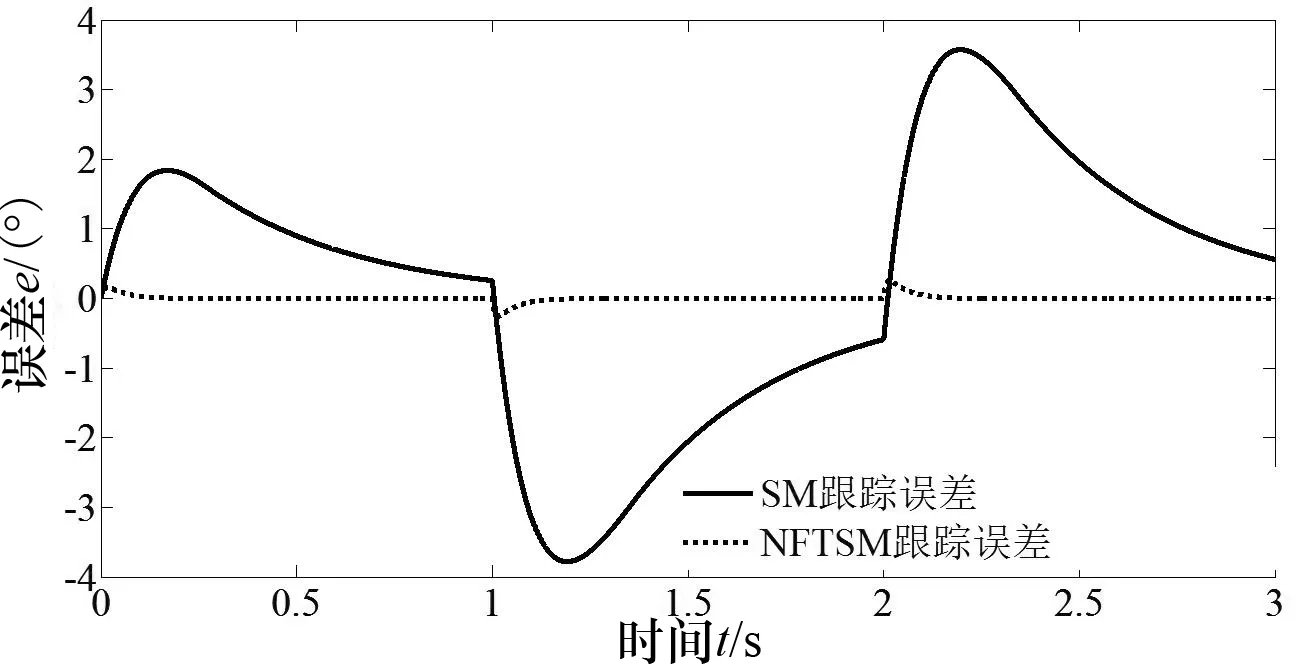
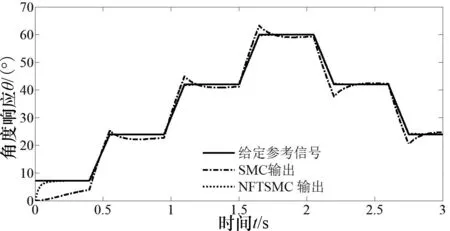
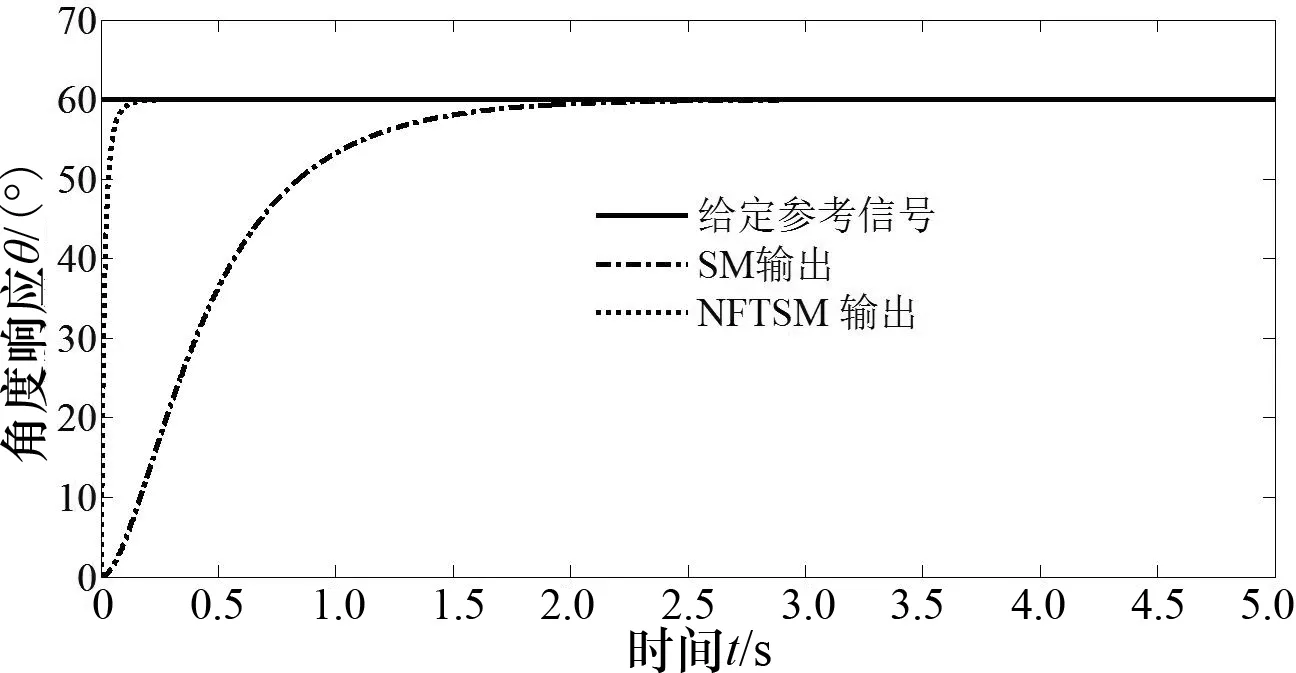
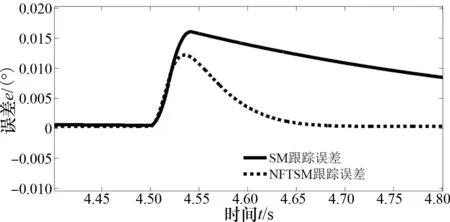
3 仿真实验





4 结 论
