基于固定共同题方法的IRT等值模型比较研究

张泉慧 张颖 何佳 邹杰文 王娇艳

（国家医学考试中心，北京 100097）

基于固定共同题方法的IRT等值模型比较研究

张泉慧 张颖 何佳 邹杰文 王娇艳

（国家医学考试中心，北京 100097）

等值模型的选择是题库建设的重要环节。本研究在IRT理论框架下，选择最为常用的Logistic模型，针对医学考试某一学科测试比较三种Logistic模型下固定共同题等值方法的差异。结果表明，单参数模型对共同题的参数固定更稳定，等值的精确性优于双参数模型和三参数模型，更适合用于该学科测试。

题库；Logistic模型；等值；IRT

随着国内考试行业的发展，等值的重要性已经受到广泛关注。等值是将一个测验不同版本的分数统一在一个量表上的过程，是实现测验公平的保证，也是题库建设的重要环节。等值方法需要基于特定的理论，目前主要有经典测验理论（CTT）和项目反应理论（IRT）两种，相比CTT理论，IRT理论采用非线性模型，建立被试对项目的反应与其潜在特质之间的非线性关系，项目参数稳定，不易受被试样本的影响，而且能够提供被试能力估计的精确性指标——测验信息函数。因此，IRT理论更适用于指导等值，并在实践应用中显示出了更大的优势，这也使其成为国外大型考试应用最广泛的理论模型。

在IRT理论中，最为常用的是Logistic模型。Logistic模型包括单参数模型（1PLM）、双参数模型（2PLM）和三参数模型（3PLM）。现阶段，国内一些大型考试中也采用了IRT理论，如公共英语等级考试（PETS）、大学英语四六级考试、汉语水平考试（HSK）等，这些考试都选择了不同的模型。但对于特定的考试，选择什么样的等值模型，尚没有相关的数据论证，更多的是基于经验的判断。因此，本研究使用医学考试中的一个学科测试作为研究对象，针对Logistic三种模型下的等值结果进行比较，等值方法主要选择目前较为常用的固定共同题参数方法，该方法需要固定共同题的参数，从而使两卷数据通过共同题的数据连接起来，位于统一的量表中。最后通过比较共同题固定前后的变化来评价等值的精确性，共同题固定得越好，说明这种等值模型越稳定，也就越适合于该测试，这一尝试也将为该学科的题库建设起到一定的铺垫作用。

1 研究对象与方法

1.1 研究对象

本研究使用同一类别、同一学科的两个年度的试卷，其中1份为标杆卷（设为Y卷），1份为待等值卷（设为X卷），试卷题目数量为66道，两卷包含14道共同题。

1.2 研究方法

本研究采用固定共同题方法进行等值，软件使用BILOGⅢ软件。研究中需要先估计标杆卷（Y卷）的参数（在BILOG中，参数是通过EM算法求解似然方程而得到的极大似然估计值）；然后，将Y卷共同题的参数固定，再估计待等值卷（X卷）的参数；虽然这一等值方法试图完全固定标杆卷中的已知参数，但在等值过程中，已知参数还是会随着等值的迭代而发生一些变化，所以最后我们通过分析这些变化的差异，对不同模型下的估计精确性进行比较。

2 研究结果

2.1 考生背景的描述统计

考生背景的描述统计如表1所示。

由表1可知，两卷样本量相近，不同背景的考生人数及比例也比较接近，说明该考试在年度间的群体没有较大变化，相对稳定。

2.2 试卷的单维性

两卷因素分析结果如表2所示。

在表2中，比较两份试卷的相关系数值与偏相关系数值，其KMO检验值接近1，说明样本采集充足度高，因素分析的结果可以接受。对两份试卷的相关系数矩阵进行Bartlett球形检验，P＜0.01，即相关矩阵不是一个单位矩阵，使用因子分析模型适宜。分析表中比值，试卷的第一特征值均超过第二特征值的3倍。根据Hambleton和Swaminathan的单维性检验标准[1]，第一特征值大于第二特征值的3倍，就可以认为测验是单维的。由此判断，该试卷考查的潜在特质是单一的，考生的作答主要受到考查特质的影响。这符合IRT理论的基本假设。

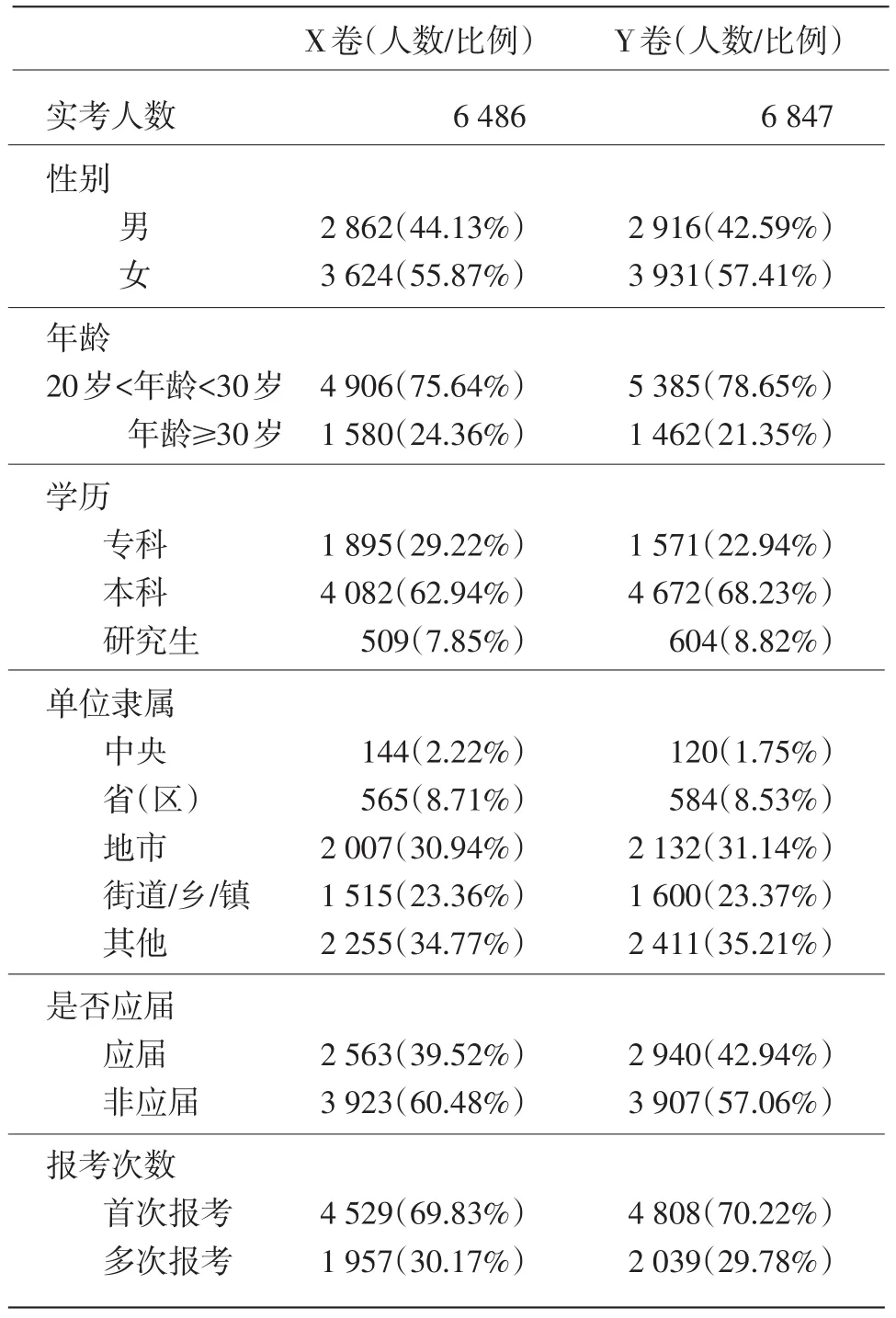
表1 考生背景描述统计

表2 两卷因素分析结果

2.3 试卷参数信息

2.3.1 共同题信息

每份试卷中均包含14道共同题，共同题与总卷的相关系数见表3，其中共同题均来自Y卷。

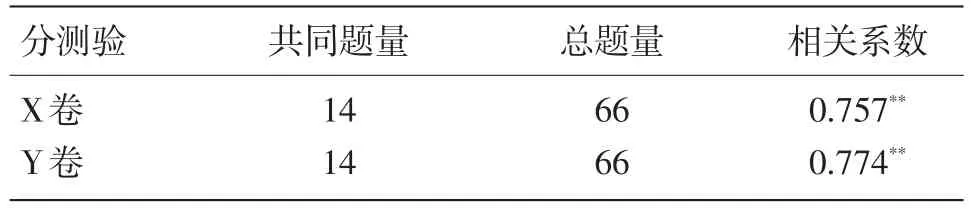
表3 共同题相关分析结果

按IRT理论来进行测验等值设计时，要求共同题应具有良好的代表性，与测验有较高的相关，题数不应少于题目总数的1/5。据表3显示，共同题与试卷之间的相关较高，题数超过1/5，说明共同题代表性良好，满足等值的要求。

2.3.2 参数估计结果

参数估计前，删去了试卷中缺考或全部答错的被试样本，三种模型下的估计结果见表4。

从整体来看，各试卷的样本量充足，完全满足IRT理论的样本量要求。三个模型下的参数估计结果并不相同，这和函数解析式不同有关，因为不同的模型中参数数量不同，对项目特征曲线的描述也会不同。总体来看，各模型中试卷平均b值大都在（-1.5，1.5）的区间内，2PLM和3PLM中平均a值都在0.4以上，3PLM中的平均c值小于0.25，说明试卷整体难度适中，区分度良好，猜测度低，质量良好。

对于试卷中的每一道题目，BILOG输出结果中都包含拟合度检验值（当测验题目大于20个，拟合度选择似然比统计量G2值计算）和每道题所提供的信息函数值。以一道试题为例，结果见表5。

分析表5，该题在三个模型中的拟合度均良好，拟合度良好的指标为Chi-sq值较小，PROB值＞0.01，提供的信息函数值（Info）较大。具体来看，该题在1PLM中的Chi-sq值最小，PROB值最大，Info值也最大，其次为2PLM，最后为3PLM。可见，对于这道题，三个模型均适合，以1PLM的拟合度为最优。

2.4 三种模型下的等值结果

等值中的迭代会使Y卷中需要固定的共同题参数发生变化，通过分析这些变化的差异，可以对方法的精确性进行比较。三个模型下的共同题变化如表6～表8所示。

将表6～表8中共同题的绝对偏差求平均，得到平均差异量（见表9），可知固定共同题参数法在三个模型中的等值存在差异，共同题固定的情况是：（1）b值以1PLM最优，参数值在等值前后仅有微小变化，其次为3PLM，而在2PLM中b值出现较大偏差，这主要是因为第9道共同题发生了严重的参数漂移，使得整体误差急速增大，除去该题目，其余题目固定较好，平均差异量为0.026，但这一数值也依然是三个模型中变化差异最大的。（2）a值比较：2PLM的差异量比3PLM小，这是因为3PLM中许多题目的a值发生了较大的漂移。（3）3PLM中c值的平均差异量为0.053，虽然数值变动在小数点后2位，但由于c值的变化范围很小，大致在（0，0.5）之间，所以微小的变化都会引起偏差。

表4 试卷平均参数信息

表5 项目参数估计信息

综上所述，随着模型参数的增加，计算愈加复杂，参数漂移的现象开始出现，这样就使得等值结果受到影响，可以设想如果随着多份试卷的等值并进入题库，误差会逐渐增大并不断累积。为了有效控制误差，保证等值的精确性，采用单参数模型是最佳的选择。

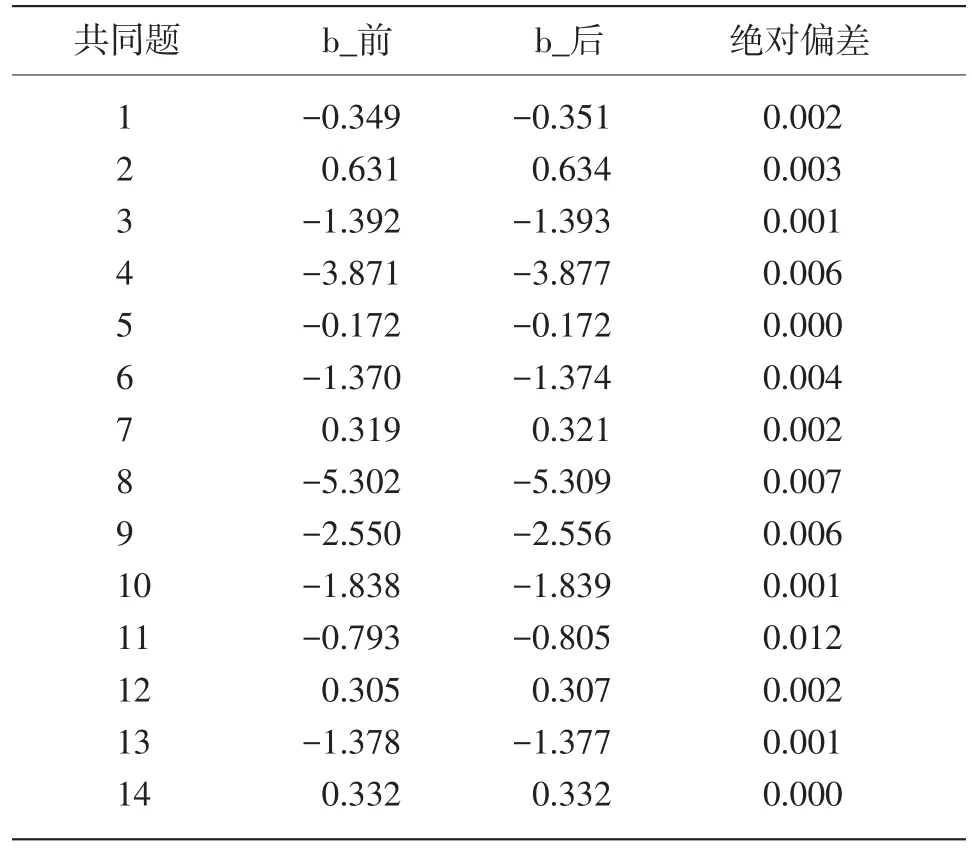
表6 1PLM模型中等值前后的共同题变化（b值）

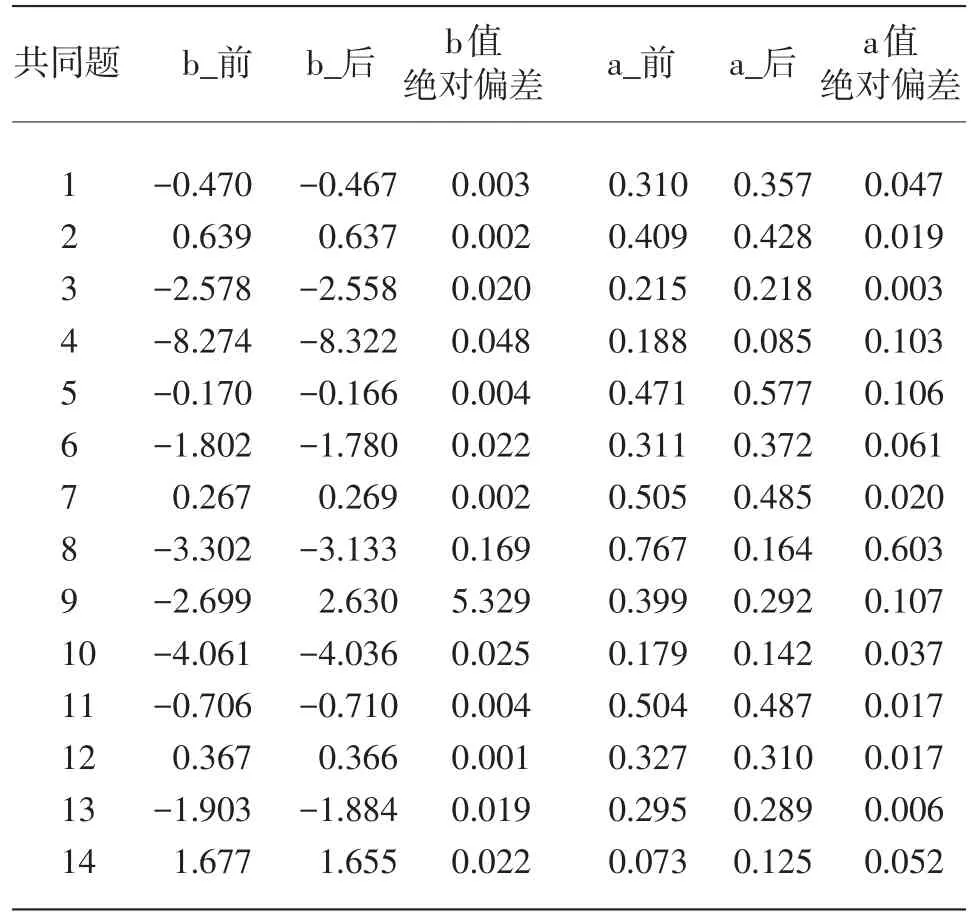
表7 2PLM模型中等值前后的共同题变化（b值/a值）

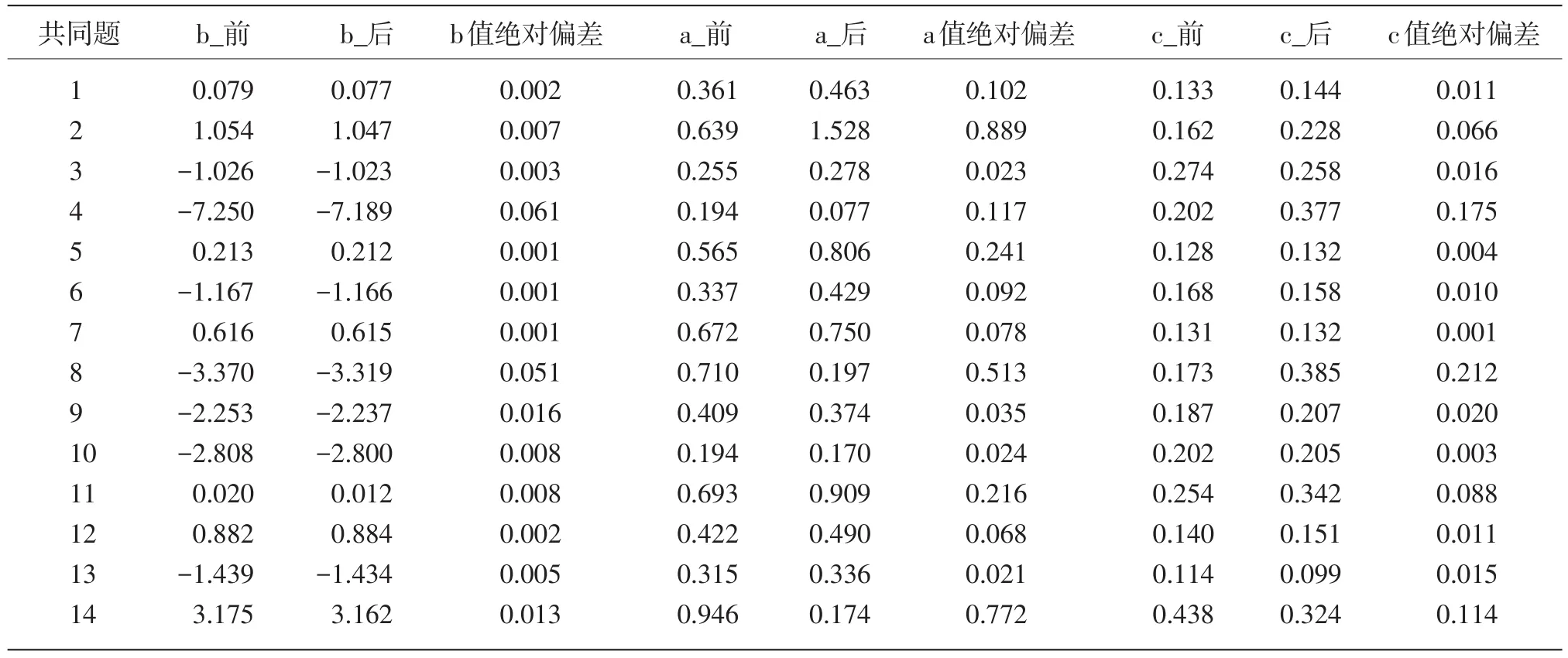
表8 3PLM模型中等值前后的共同题变化（b值/a值/c值）

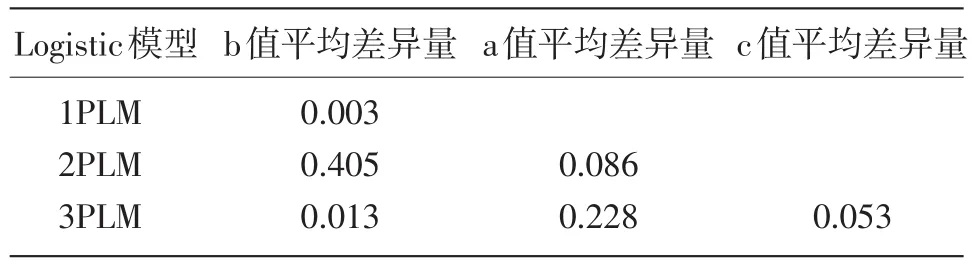
表9 三种模型下的共同题平均差异量比较

3 讨论

有关IRT等值模型的选择，在学术界并没有定论。单参数模型比较简单，使用较为方便，但它对项目参数性质的要求较多，比如区分度大致相同、猜测度很小等；2PLM要求项目的猜测度较小；3PLM涵盖较多项目信息，但参数估计更为繁杂。从题目的拟合度来看，由于3PLM增加了猜测度参数，对曲线的拟合程度更高，所以相比其他模型的总体拟合度要高；而2PLM比单参数模型增加了区分度指标，所以总体的拟合度也相对1PLM要好。但是参数的增加必然会增加估计误差。漆书青、戴海琦、丁树良在专著中也曾提到：尽管三参数模型在资料拟合上显示出很大优越性，但其参数估计很复杂，且单参数模型对伴随参数存在充分估计量，这是三参数模型无法比拟的。因此，选择模型时还需要结合具体情况来分析[2]。因此在本研究通过比较等值的稳定性，即共同题等值前后的变化差异来选择模型。数据表明，单参数模型等值的稳定性更好，参数固定的误差最小，运算更简单可行，因此最适合用于该学科测试。

此外，我们还发现等值过程中参数漂移现象，这说明参数变化超过了随机误差可以解释的范围。具体原因是，共同题在两个测验形式中所发挥的功能或不一致，虽然在形式上还是同一题目，但已无法起到媒介或链接的作用，这种共同题给等值带来的是一种系统误差。由于参数漂移的影响因素很多，如果简单剔除题目，也会引入误差，因此，本研究中并未删除漂移题目，而是将漂移的原因探讨作为进一步的研究方向。

[1]HAMBLETON R K,SWAMINATHAN H.Item response theory:Principles and applications[M].Boston,MA:Kluwer-Nijhoff，1985.

[2]漆树青,戴海崎,丁树良.现代教育与心理测量学原理[M].北京:高等教育出版社,2002.

A Comparative Study of IRT Equivalence Model Based on Fixed Common Item Parameters Method

ZHANG Quanhui,ZHANG Ying,HE Jia,ZOU Jiewen,WANG Jiaoyan
（National Medicine Examination Center,Beijing 100097,China）

Choosing a certain measurement model is an important part of constructing item bank.This study attempts to analyse the differences in three types of Logistic model by fixed common item parameters method under the IRT theory.The object of study is some kind of medical examination.The result is that the method of 1PLM is more stable,the parameters is smaller than 2PLM and 3PLM,so the 1PLM is suitable in this examination.

Item Bank；Logistic Model；Equivalence；IRT

G405

A

1005-8427（2017）06-0065-5

10.19360/j.cnki.11-3303/g4.2017.06.011

（责任编辑：周黎明）

张泉慧（1982—），女，国家医学考试中心，助理研究员；

张 颖（1973—），女，国家医学考试中心，研究员；

何 佳（1973—），女，国家医学考试中心，副研究员；

邹杰文（1986—），女，国家医学考试中心，实习研究员；

王娇艳（1984—），女，国家医学考试中心，助理研究员。