弹性连接失效对大跨斜拉桥地震响应影响*

2017-09-12焦常科李爱群伍小平

振动、测试与诊断 2017年4期

关键词：加劲梁主塔斜拉桥

焦常科,李爱群,伍小平

(1.上海建工(集团)总公司上海,200080)(2.东南大学土木工程学院南京,210096)(3.北京建筑大学土木与交通工程学院北京,100044)

弹性连接失效对大跨斜拉桥地震响应影响*

焦常科1,2,李爱群2,3,伍小平1

(1.上海建工(集团)总公司上海,200080)(2.东南大学土木工程学院南京,210096)(3.北京建筑大学土木与交通工程学院北京,100044)

首先,以附加弹性连接(elastic connection,简称EC)的线性单自由度(single degree of freedom,简称SDOF)系统为例，研究弹性连接的失效对系统动力时域响应的影响；其次，以一座半漂浮体系的大跨斜拉桥在两组地震作用下的地震响应为例，研究塔(墩)梁间弹性连接失效对大跨斜拉桥结构地震响应的影响。研究表明：弹性连接失效对大跨桥梁动力响应存在重要影响，动力响应存在明显差异；考虑弹性连接失效后，如果在地震中弹性连接出现失效，大跨斜拉桥加劲梁地震内力明显小于未考虑弹性连接失效的情况，但加劲梁和塔顶纵桥向位移会有所增加；应当设置合理的弹性连接及其失效限值，保护主体结构在地震中的安全。

弹性连接；失效；大跨斜拉桥；地震响应

引言

塔/墩梁间纵桥向设置弹性连接在静力情况下可有效限制塔/墩梁间的因温度、行车等产生的相对位移；在地震作用下，可有效限制加劲梁过大的纵向位移，并将纵桥向地震力合理分配到塔/墩上。常见限制墩梁位移的装置包括：a.钢板连接式；b.预应力钢绞线连接式；c.缆索连接式[1]。塔/墩梁间纵桥布置的弹性连接在一定程度上改变了结构的纵桥向纵漂频率(或消除纵漂振型)，但弹性连接本身并不耗能,在拉、压过程中存储(释放)弹性势能。研究表明，对于漂浮(半漂浮)体系大跨斜拉桥，纵桥向塔(墩)梁间设置恰当的弹性连接可有效限制地震过程中塔(墩)梁间的纵桥向相对位移，避免出现落梁；在弹性连接参数合适的情况下，可有效减小桥梁的地震响应。文献[2]研究了七塔斜拉桥(跨径布置为100m+200m×6+100m)塔梁间纵桥向3种连接方式下的地震响应特点，包括漂浮、弹性连接和双线型弹簧连接。焦驰宇等[3]基于Sap2000平台，采用反应谱法分析了塔梁间弹性索刚度变化引起斜拉桥地震反应变化的力学机理。包立新等[4]在评价宜宾长江公路大桥斜拉桥抗震性能时，认为其抗震结构体系采用“弹性索梁-塔连接体系”是合适的。与局部斜拉索松弛不同[5]，作为桥梁整体结构的关键构件之一，塔梁间纵桥向布置的减震装置失效对结构地震响应具有重要影响。

国内外学者针对塔梁间设置单个或多种被动减震控制装置对大跨斜拉桥地震响应的减震控制效果开展了广泛研究[6-10]，但该类减震装置失效对大跨斜拉桥动力响应的影响方面研究相对较少。大跨斜拉桥一般具有密集的低频振动模态，因而其地震响应受地震输入特性的影响较大；塔/墩梁间增加弹性连接会影响桥梁的前几阶振型，进而影响结构的地震响应。弹性连接在动态变形过程中，存储的弹性势能会在下一个反向变形中释放出来。一旦出现意外失效，将会导致大跨斜拉桥地震响应出现突变，由此可能对结构造成严重震害。笔者首先以线性单自由度系统的附加弹性连接失效后，分析附加弹性连接失效对其动力响应的影响；其次，以一座半漂浮大跨度斜拉桥为例，研究塔/墩梁间弹性连接失效前后大跨斜拉桥地震响应的特点。

1 SDOF系统动力响应

以SDOF线性(m，k，ξ)系统为例，其布局如图1所示。结构参数以及与之并联的弹性连接参数如表1所示。动力平衡方程如式(1)所示，其中：u为质点m相对地面位移；g(k0t+Δtu,f0)为弹性连接的回复力项；k0为弹性连接刚度；f0为弹性连接的失效荷载。当式(1)中首次出现|k0t+Δtu|≥f0时，该回复力项g(k0t+Δtu,f0)=0，以此作为弹性连接失效的依据。基于Newmark-β法编制Fortran程序对式(1)进行时域动力求解。

表1 SDOF系统参数Tab.1 Parameters of SDOF system

(1)

图2 SDOF动力响应对比Fig.2 Comparison of dynamic response of SDOF

当结构受到El-centro波(峰值调整为3m/s2)作用时，其位移响应时程如图2(a)所示。结构本身的弹性回复力与弹性连接EC的内力如图2(b)(c)所示。可见：a.在上述系统参数下，EC起到了减震效果，位移响应有所减小；b.EC失效后,结构的位移响应出现分叉，在随后的振动时间内，其位移响应逐渐与原结构一致;c.EC失效后，结构的动力特性发生变化，结构响应与EC失效后的动力特性以及地震输入特性直接相关，应当引起注意;d.EC内力首次超过限定值后，其内力衰减至0，如图2(c)所示，作为失效处理。EC失效后，结构回复力有所增大，并在后继的时间内逐渐衰减。

由线性SDOF系统(m，k，ξ)的动力放大系数[11]可见，回复力刚度k减小后，系统动力放大系数随激励频率比的变化出现明显偏移。对应漂浮/半漂浮体系的大跨度斜拉桥，在塔梁/墩梁处设置纵桥向弹性连接后，全桥动力特性发生变化，因而影响结构动力特性；加劲梁纵桥向变形过大时，可能会导致弹性连接的失效，也会引起动力响应的变化。

2 有限元模型

图3 有限元模型Fig.3 Finite element model of the bridge

以上海闵浦大桥为例，建立该桥的脊骨梁有限元模型如图3所示[12]。其中:TW与TE分别为浦东与浦西侧主塔；两侧的辅助墩编号分别为PWj和PEj(j=1,2,3,4)；全桥长为1 212 m；跨径布置为63m×4+708m+63m×4，边跨侧各有4个辅助墩。塔、梁、墩均采用Beam单元模拟，斜拉索采用只受拉Truss单元模拟；塔梁处布置的8个非线性黏滞流体阻尼器采用非线性Dashpot单元模拟。在结构静力初始平衡态(Initial Base State)的基础上进行动力分析。特征值分析表明该桥纵飘振型、一阶侧弯、一阶竖弯振型频率分别为0.082 75，0.257 5和0.285 47 Hz。主塔及辅助墩处布置的弹性连接基本参数如表2所示。笔者选取Tianjin和El-centro两组地震波作为输入。动力时程分析中，上述地震波的峰值均调整为0.15g。

表2 弹性连接参数Tab.2 Parameters of EC

图4 Tianjin波作用下桥梁主要地震响应Fig.4 Seismic response of the bridge under Tianjin motion

3 弹性连接失效分析

Tianjin和El-centro两组地震作用下，加劲梁轴力和竖向弯矩正、负向峰值包络沿桥长的分布、塔顶纵桥向位移及跨中纵桥向位移时程如图4和图5所示。不考虑弹性连接失效时，加劲梁轴力明显大于考虑弹性连接失效时的轴力；前者在主塔处出现明显的突变，如图4(a)和5(a)所示，因为弹性连接在纵桥向对加劲梁形成了有效的弹性约束，可直接将加劲梁的纵向地震作用传递给了主塔下横梁。中跨加劲梁横桥向弯矩不考虑弹性连接失效时，其双向数值明显大于考虑弹性连接失效的情况，如图4(b)和5(b)所示。主塔处弹性连接先于辅助墩处弹性连接失效，弹性连接失效值与表2所示一致(如图6所示),失效时刻与塔(墩)梁间相对位移峰值首次达到失效位移(f0/k0)有关。两组地震作用下，主塔处弹性连接失效时刻分别为7.215s和2.049s。弹性连接失效后，结构体系内出现能力释放及结构体系变化，加劲梁跨中及塔顶纵桥向位移时程会出现突变，随后该位移在斜拉索的对称布置下，逐渐回复到平衡位置处。考虑弹性连接失效后，如果地震中出现弹性连接失效，加劲梁和主塔顶部的纵桥向位移响应峰值会明显增大，源于主塔或辅助墩对加劲梁纵桥向的约束减弱，并由加劲梁导致主塔顶纵桥向位移响应增大，如图4(c)(d)和5(c)(d)所示。Tianjin波坐下加劲梁的内力及位移响应明显大于El-centro波下的加劲梁内力，源于前者在低频范围内更能激起结构的动力响应。设置适当的弹性连接刚度和失效内力限值对有效减小加劲梁地震内力有一定的作用，并且以弹性连接失效来消耗能量，起到保护主体结构的作用。但是，弹性连接的失效会导致塔(墩)梁间的约束减弱，并在弹性连接失效瞬间结构体系发生改变，内力瞬间释放出来，加劲梁纵桥向位移响应增加较为明显，这一点应当引起充分重视。

在考虑弹性连接失效情况下，Tianjin和El-centro两组地震作用下，辅助墩(PW1/PW2/PW3/PW4)墩顶及主塔(TW)处的弹性连接内力时程及失效状态如图6所示。其中:0值对应EC未失效；1值对应EC失效。

图5 El-centro波作用下主梁地震响应Fig.5 Seismic response of the bridge under El-centro motion

在Tianjin波和El-centro波作用下，主塔纵桥向位移、剪力及纵桥向弯矩的双向峰值包络及主塔与辅助墩基底纵桥向反力时程如图7和图8所示。考虑弹性连接失效后，主塔下塔柱纵桥向内力明显有所减小，除塔顶局部负向位移外，整体塔身纵桥向位移均有所减小，主要原因在于弹性连接失效后，塔梁间的纵桥向约束作用有所减弱。弹性连接失效后，加劲梁的纵桥向地震作用主要通过斜拉索传递给主塔。两组地震波作用下，考虑弹性连接失效后，主塔基底纵桥向反力峰值明显减小。Tianjin波作用下，边墩PW4基底纵桥向反力出现与主塔类似的现象；但El-centro波作用下，边墩PW4基底纵桥向剪力出现与主塔相反的现象，并且基底剪力在墩顶弹性失效后出现明显的短时震荡现象，如图7(a)(b)和8(a)(b)所示。边墩PW4处的弹性连接失效前，墩顶受到加劲梁纵桥向的约束和竖向压力。弹性连接失效后，纵桥向的弹性约束解除，其动力响应与边墩PW4的纵桥向侧弯振型和地震输入特性有关。

4 结论

1) 考虑弹性连接失效后，如果在地震中弹性连接内力超过其失效限值而出现失效，由于塔梁/墩梁见的约束减弱，结构的动力响应存在明显差异；大跨斜拉桥加劲梁地震内力明显小于未考虑弹性连接失效的情况，但加劲梁和塔顶纵桥向位移会有所增加。

2) 漂浮/半漂浮体系大跨斜拉桥的纵桥向弹性连接失效后，加劲梁的纵飘振型可能会较为明显，该体系转换会导致结构响应出现明显变化和局部的突变；结构的地震响应对地震输入具有较为明显的依赖性，应选择适合桥址场地特性的地震输入。

图6 弹性连接内力时程及失效状态Fig.6 Time history of internal force and the status of EC

图7 Tianjin波作用下主要地震响应Fig.7 Seismic response of the bridge the ground motion of Tianjin

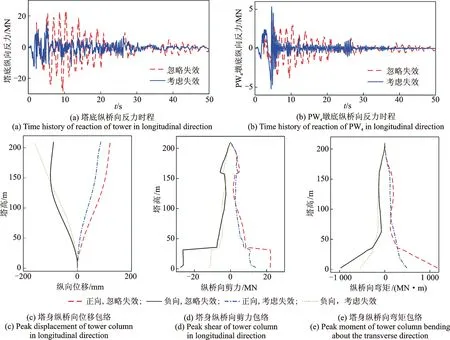
图8 El-centro波作用下主塔内力、位移峰值响应及主塔与辅助墩基底反力时程Fig.8 Seismic response of the bridge the ground motion of El-centro

3) 在确定塔梁/墩梁间的纵桥向弹性连接参数时，应给出相应的允许限值，以确定在进行地震响应计算中是否需要考虑弹性连接的失效。

[1] CJJ 166—2011 城市桥梁抗震设计规范[S].北京:中国建筑工业出版社,2011.

[2] Okamoto Y,Nakamura S.Static and seismic studies on steel/concrete hybrid towers for multi-span cable-stayed bridges[J].Journal of Constructional Steel Research,2011,67(2):203-210.

[3] 焦驰宇,李建中,彭天波.塔梁连接方式对大跨斜拉桥地震反应的影响[J].振动与冲击,2009,28(10):179-184.

Jiao Chiyu,Li Jianzhong,Peng Tianbo.Effects of different connecting styles between towers and deck on seismic responses of a long-span cable-stayed bridge[J].Journal of Vibration and Shock,2009,28(10):179-184.(in Chinese)

[4] 包立新,李小珍,卫星,等.宜宾长江公路大桥斜拉桥抗震性能评价[J].工程力学,2008,25(2):174-182.

Bao Lixin,Li Xiaozhen,Wei Xing,et al.Evaluation of seismic resistance capacity for Yibin Yangze river cable-stayed bridge[J].Engineering Mechanics,2008,25(2):174-182.(in Chinese)

[5] Wu Q,Takahashi K,Nakamura S.The effect of cable loosening on seismic response of a prestressed concrete cable-stayed bridge[J].Journal of Sound and Vibration,2003,268:71-84.

[6] Casciati F,Cimellaro G P,Domaneschi M.Seismic reliability of a cable-stayed bridge retrofitted with hysteretic devices[J].Computers and Structures,2008,86:1769-1781.

[7] Soneji B B,Jangid R S.Passive hybrid systems for earthquake protection of cable-stayed bridge[J].Engineering Structures,2007,29(1):57-70.

[8] Casciati F,Cimellaro G P,Domaneschi M.Seismic reliability of a cable-stayed bridge retrofitted with hysteretic devices[J].Computers and Structures,2008,86:1769-1781.

[9] Martinez-Rodrigo M D,Filiatrault A.A case study on the application of passive control and seismic isolation techniques to cable-stayed bridges:a comparative investigation through non-linear dynamic analyses[J].Engineering Structures,2015,99:232-252.

[10]Vader T S,McDaniel C C.Influence of dampers on seismic response of cable-supported bridge towers[J].Journal of Bridge Engineering,2007,5:373-379.

[11]Clough R W,Penzien J.Dynamics of structures[M].New York:Computers and Structures,Inc,2004:37-38.

[12]焦常科,李爱群.大跨斜拉桥多点激励随机地震响应研究[J].振动工程学报,2013,26(5):707-714.

Jiao Changke,Li Aiqun.Research on random seismic response of long-span cable-stayed bridge under multi-excitation[J].Journal of Vibration Engineering,2013,26(5):707-714.(in Chinese)