舰载反潜直升机吊放声纳区域反潜策略建模*

常 波，周晓光，田怀英，李 莹

（海军航空兵学院，辽宁 葫芦岛 125001）

舰载反潜直升机吊放声纳区域反潜策略建模*

常 波，周晓光，田怀英，李 莹

（海军航空兵学院，辽宁 葫芦岛 125001）

为提高舰载反潜直升机吊放声纳区域反潜搜索作战效能，对舰载反潜直升机吊放声纳区域反潜搜索策略问题进行了建模。根据潜艇目标位置信息的不确定性，研究了潜艇目标位置信息的概率分布函数，采用Markov状态转移概率矩阵描述了潜艇目标位置信息变化的方法。其次，给出了基于贝叶斯理论的潜艇目标信息概率分布函数更新公式。再次，推导了舰载反潜直升机吊放声纳区域反潜最优策略，给出了舰载直升机吊放声纳区域反潜搜索算法。最后给出了典型案例，验证了反潜搜索策略的有效性。研究成果可为舰载反潜直升机吊放声纳区域反潜提供决策依据。

反潜直升机，搜索策略，贝叶斯理论

0 引言

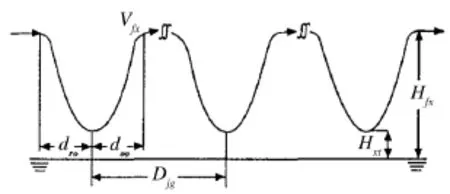
图1 吊放声纳搜索飞行剖面图

舰载反潜直升机作为海军重要的反潜装备，具有速度快、效率高等特点，一直倍受各国海军的重视。舰载反潜直升机一般采用应招搜潜方式，获取敌方潜艇目标信息后，飞往发现潜艇目标的海域，执行搜索、跟踪、攻击任务。舰载反潜直升机的反潜设备一般包括吊放声纳、浮标和磁探等设备［1］，能在短时间内搜索大面积的海域，准确探测潜艇目标位置。舰载反潜直升机使用吊放声纳搜索潜艇，一般采用边前进边逐点探测的方法，其飞行搜索作业剖面如图1所示［2］。舰载反潜直升机到达搜索海域后，按预定的搜索航线飞行，飞行高度一定在100 m以上，速度为100 kn。接近第一个探测点时，降低飞行高度和速度，当悬停点下降到高度小于50 m时，迎风悬停，放置吊放声纳，开机探测目标，监听2 min～3 min，如果没有发现目标，收起水下分机爬升到一定高度，增速，飞向第2个探测点，重复搜索操作。影响舰载反潜直升机吊放声纳搜索效能的因素很多，搜索路径是其中重要的因素之一。本文在分析潜艇目标概率分布的基础上，采用Markov状态转移概率矩阵描述潜艇目标位置信息变化，推导了舰载反潜直升机吊放声纳区域反潜最优策略，给出了舰载直升机吊放声纳区域反潜搜索算法，研究结果可为舰载反潜机反潜作战提供理论决策依据。

1 潜艇目标的概率分布

假定没有获取潜艇目标的任何位置信息，那么一般采用在搜索海域的均匀分布描述潜艇目标分布信息。对于应招搜索问题，假定潜艇目标的速度为V，在给定航向的均值时间为，总时间为 t，那么潜艇目标分布的概率密度函数为［3］：

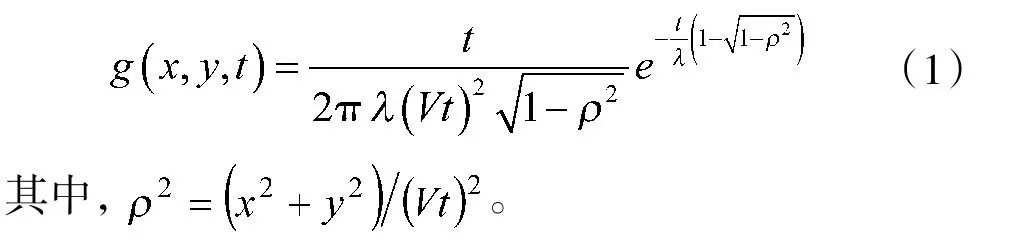
应用式（1），潜艇目标概率分布与时间t的关系如图2所示。图2中对比了10 min和20 min的目标分布状况。从图2中可以看出，20 min后的潜艇目标概率分布更加平缓，即目标分布的海域更大，为搜索带来更大的困难。

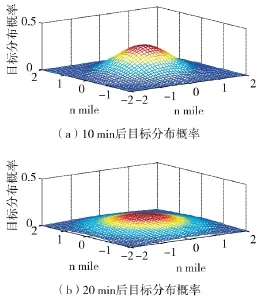
图2 目标分布概率

2 舰载反潜直升机区域反潜搜索作战建模

将搜索海域进行栅格化，假定存在n个单位区域栅格，如图3所示。潜艇目标初始位于栅格i的概率为 pi，其中。在离散时间（阶段），目标从栅格之间移动。如果在时刻t，目标在栅格i内，在时刻t+1目标移动到栅格j的概率为 pij，其中为Markov状态转移概率矩阵。

图3 搜索海域栅格

舰载反潜直升机执行贯序搜索。在时刻t，决定对某一栅格进行搜索，搜索过程持续到发现目标或者接到停止搜索命令为止。搜索栅格i的消耗为ci＞0，如果目标位于栅格i内，那么舰载直升机搜索栅格i发现目标的概率为αi。舰载直升机搜索的目的是在给定搜索次数的条件下，最大化发现目标的概率。或者最小化搜索损耗。一个舰载反潜直升机反潜策略是一个规则，即确定何时搜索哪一个栅格。搜索策略用描述，其中。根据搜索策略δ，在i阶段舰载反潜直升机将对δi栅格进行搜索。s=0意味舰载反潜直升机将立即停止搜索；s=∞的意思是舰载反潜直升机发现目标后才能停止搜索行动。

对于任何策略δ，状态概率P，整数m定义如下函数：

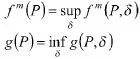
从定义可知：

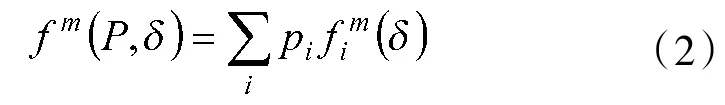
其中，T为状态转移概率矩阵。

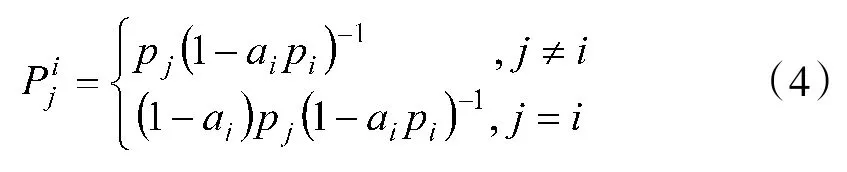
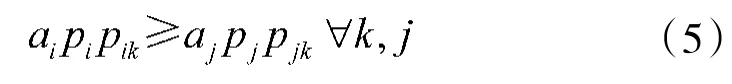
那么最大化第m（给定整数）次搜索发现目标的概率，最优的搜索策略是首先搜索栅格i。

证明：

设δ为任意搜索策略。对于任何栅格j，设Sjδ为首先搜索栅格j，之后采用搜索策略δ。假定栅格i是满足定理1的栅格，那么有：

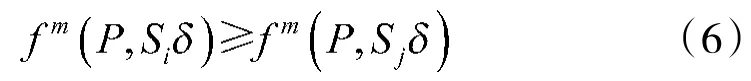
对于任务栅格j，任何策略δ，定理定义如下：

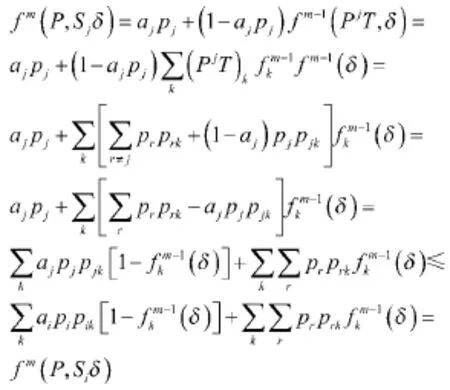
存在两个特殊情况：

根据定理1，如果潜艇目标初始位于栅格i的概率为 pi，其中，潜艇目标状态转移矩阵为，如果目标位于栅格i内，那么舰载直升机搜索栅格i发现目标的概率为αi，那么舰载反潜直升机区域反潜搜索最优算法如下：

①设m=1。

②选择搜索栅格i满足如下条件：

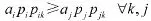
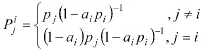
④m←m+1，返回步骤②。

⑤结束。

以下研究ai≡1，即舰载反潜直升机具有完全的探测能力的最优探测策略。

定理2.假定ai≡1，为最大化第m次搜索发现目标的概率，如果在目标状态为，最优的搜索策略是栅格i。那么在潜艇目标分布概率为，如果，且，其中，最优的搜索策略仍然是首先搜索栅格i。

证明：对于任何搜索策略δ和栅格j，设Sjδ为搜索策略，首先搜索栅格j然后采取策略δ。那么对于任何状态P，有如下公式：

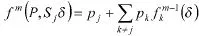
设栅格i为满足定理2的栅格，假定首先搜索栅格i，然后采取最优的策略δ*是状态分布P的最优搜

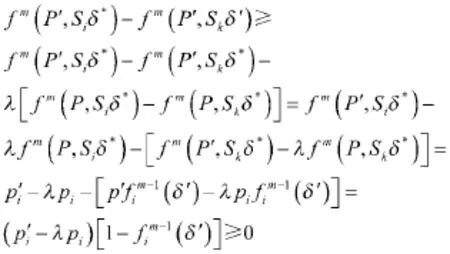
3 典型案例分析

3.1 基本想定

假定某一海域发现水面状态潜艇一艘，随即敌潜艇进入水下状态，假定潜艇2 kn。反潜直升机接受命令到飞往目标区域的时间为20 min，飞行速度为180 km/h，反潜直升机携带吊放声纳反潜装备，调放声纳作用距离为5 n mile，发现目标的概率为75豫。根据反潜直升机反潜作战能力，将搜索海域划分为5*5的25个方格。假定搜索海域为20 n mile*20 n mile，根据反潜掉放声纳的作用距离，将搜索海域划分为3*3方格，共有9个栅格，概率分布函数为：P=［0.075 0.1 0.075 0.1 0.3 0.1 0.075 0.1 0.075］。栅格集合C和邻接区域栅格集合Ci为：，

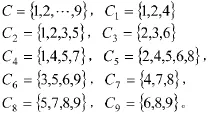
假定目标仍停留在原始栅格的概率为0.4，移动到邻接栅格的概率为0.6/mj，其中mj为栅格j的邻接栅格数量。所以状态转移矩阵为：

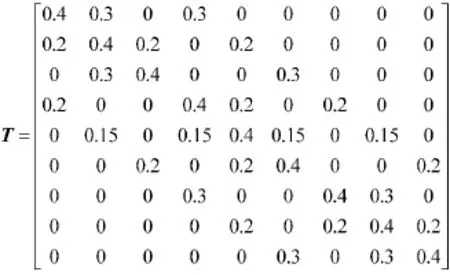
3.2 仿真结果分析

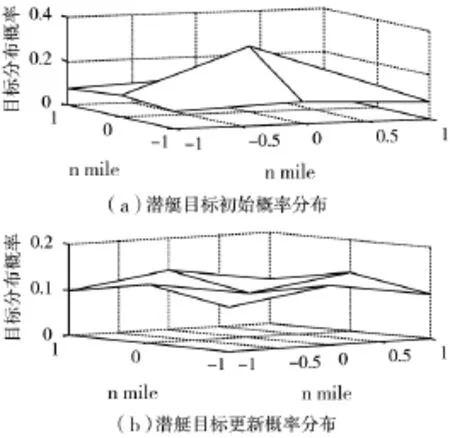
图4 潜艇目标概率分布函数

应用最优舰载反潜直升机反潜搜索算法，迭代10次，图4显示了潜艇目标概率分布函数的更新。根据最优反潜算法，舰载反潜直升机首先搜索栅格5，没有搜索到目标，更新潜艇目标的概率分布，如图 4（b）所示，从图 4（b）可以看出，栅格 5的概率分布是最小的。

根据最优反潜算法，第2次搜索的栅格为2，第3次搜索的栅格为4，最优的搜索策略为5，2，4，6，8，1，3，5，7，9，如图 5 所示。

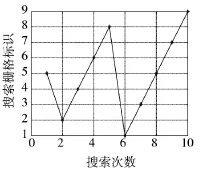
图5 舰载反潜直升机搜索策略

4 结论

本文对舰载反潜直升机吊放声纳区域反潜问题进行了建模研究，制定了舰载反潜直升机吊放声纳区域反潜最优搜索策略，该策略基于潜艇目标的初始概率分布，并根据舰载反潜直升机的搜索结果对潜艇目标概率分布进行更新，该策略较好的利用了先验概率知识和后验概率知识，具有较好的实用性和应用性。

［1］丛红日，勒天宇，刘卫东.吊放声纳搜索效能通用仿真模型研究［J］.系统仿真技术，2001，7（1）：72-75.

［2］金惠明，李建勋.反潜直升机吊放声纳搜潜策略分析［J］.电光与控制，2011，18（8）：26-30.

［3］郭辉，钱学东，刘启军.直升机吊放声纳搜潜机动建模仿真［J］.指挥控制与仿真，2009，31（1）：87-91.

［4］丛红日，王宗杰.反潜直升机应召搜索区模型研究［J］.舰船电子工程，2010，30（9）：48-52.

［5］KUNIGAMI M.Optimizing asw search for HVU protection using the FAB algorithm［D］.Monterey，California:NAVAL Postgraduate School，1997：45-50.

［6］DANSKIN J M.A helicopter versus submarine search game［R］.1401 Wilson Boulevard，Arlington，Virginia，Center for Naval Analyese，1966：66-68.

［7］CHEN H，SHEN D.Tracking evasive objects via a search allocation game ［J］.Marriott Waterfront，Baltimore，MD，USA，2010 American Control Conference，2010，10：33-36.

［8］FEWELL M P ，OZOLS S.Simple detection performance analysis of multistatic sonar for anti-submarine warfare［R］.

Edinburgh South Australia 5111 Australia .Maritime OperationsDivision Defence Science and Technology Organisation.2011.06：88-90.

［9］SCOTT D S.Game-theoretic anti-submarine warfare mission planning［D］.Monterey，California 93943:NAVAL Postgraduate School，2009：167-168.

［10］ROBBINS D L.Decision-making process of an antisubmarine warfare commander［D］.Monterey，California 93943，Naval Postgraduate School，1986：70-72.

［11］ASSAF D，SHARLIN B A.Dynamic search for amoving target［J］.Appl Probab，1994（31）：438-457.

Modelling and Research on Area Searching Strategies for Antisubmarine Helicopter With Dipping Sonar

CHANG Bo，ZHOU Xiao-guang，TIAN Huai-ying，LI Ying
（Naval Aviation Institute，Huludao 125001，China）

In order to improve operational efficiency of area searching for antisubmarine helicopter with dipping sonar，the area searching strategies for antisubmarine helicopter with dipping sonar is modeled and researched.Firstly，because of the uncertainty of submarine position information，the probability density of submarine position is researched，and the Markov transition probility matrix is used to describle the motion of helicopter.Secondly，the new submarine position probability is updated using bayes rule.Thirdly，the optimal search strategies for antisubmarine helicopter with dipping sonar is deduced，and the search algorithm is given.Finally，experimental results demonstrate the ability and validity of the optimal search strategies.The results of this paper can provide decision support for area searching of antisubmarine helicopter with dipping sonar.

antisubmarine helicopter，searching strategy，bayesian theory

E925.4；TJ85

A

10.3969/j.issn.1002-0640.2017.08.016

1002-0640（2017）08-0068-04

2016-06-08

2016-08-05

国家社科基金（军事学）资助项目（14J003-XXX）

常 波（1974- ），男，辽宁丹东人，副教授。研究方向：仪表电气与飞控，航空兵反潜作战。