一种弧段快速更新法的精密定轨精度分析

代桃高，李建文，刘旭芳，赵 静,景 鑫

(1.信息工程大学导航与空天目标工程学院，郑州 450001；2.北斗导航应用技术河南省协同创新中心，郑州 450001；3.91650部队， 广州 510320；4.成都信息工程大学，成都 610225；4.61363部队，西安 710054)

一种弧段快速更新法的精密定轨精度分析

代桃高1,2，李建文1,2，刘旭芳3，赵 静4,景 鑫5

(1.信息工程大学导航与空天目标工程学院，郑州 450001；2.北斗导航应用技术河南省协同创新中心，郑州 450001；3.91650部队， 广州 510320；4.成都信息工程大学，成都 610225；4.61363部队，西安 710054)

针对实时卫星精密定轨解算中卫星轨道精度易随预报弧段增长而降低的问题，提出一种基于非差模型并以24 h为解算弧段的弧段快速更新方法来提高卫星轨道的更新频率，以达到准实时精密定轨效果。实验结果表明：当实测弧段以每2 h滑动更新时，实测弧段轨道精度优于5 cm；预报轨道对用户实时可用性延后4 h；绝大多数卫星在预报第4个小时至第6个小时的合成1 d轨道精度优于10 cm，理论上可用于分米级导航定位。

准实时；精密定轨；滑动窗口；非差法；预报弧段；国际全球连续监测评估系统

0 引言

用全球卫星导航系统(global navigation satellite system，GNSS)进行导航定位时需要已知卫星坐标，才能在一次同步观测中实现用户位置解算。卫星坐标的获取可通过广播星历计算或精密星历内插得到，目前，广播星历轨道精度在2 m左右[1]，国际GNSS服务(The International GNSS Service，IGS)公布的精密星历轨道实测弧段精度优于3 cm，轨道预报弧段精度随预报时长而变化，预报1 d弧段轨道精度优于10 cm[2]，预报弧段轨道可服务于dm级导航定位。IGS超快速精密星历的更新周期为6 h。更新周期的长短影响精密星历对实时定位用户的可用性，而在卫星精密定轨解算过程中，待估参数过多，庞大的系数矩阵致使解算效率较低[3]，故一般无法实现实时的精密轨道更新。为满足用户的实时应用，需进行准实时的轨道更新(用预报轨道代替实时轨道)，即需要预报一段轨道弧段，一般卫星定轨解算时间越短，预报弧段也可相应缩短。整个卫星定轨过程需要一段时间的数据准备期、产品解算期及网络延迟；所以实时定位用户直接可使用的是预报星历。目前，我国自主建设的国际GNSS连续监测评估系统(The International GNSS Monitoring & Assessment System，iGMAS)分析中心，已具备4大卫星导航系统精密定轨解算能力，同时也可提供6 h更新的超快速轨道。

本文在iGMAS分析中心精密定轨软件的基础上，基于定长弧段滑动更新方法(后文称作滑动窗口)进行每2 h更新的定轨解算，预报后24 h轨道弧段，并利用IGS公布的最终轨道产品对该预报轨道各时段进行精度分析。

1 基于非差法卫星精密定轨原理

接收机接收到的观测量主要包括码观测量P、相位观测量L及多普勒观测量D。导航卫星精密定轨一般同时基于伪距和载波的组合观测方程进行数据处理。组合观测量的方式可以是非差或双差。双差观测量是非差观测量的线性组合，二者在数学模型上等价[4]。本文采用的是非差消电离层组合观测量。

1.1 观测方程

载波相位和伪距观测量的原始观测方程为

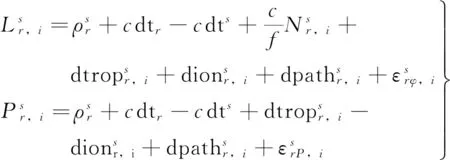
(1)

由式(1)可看出：原始观测方程包括难以用模型消除的电离层延迟误差，而基于双频的消电离层组合观测量可以较好削弱电离层的影响。本文采用消电离层组合观测量，载波相位和伪距的消电离层公式为

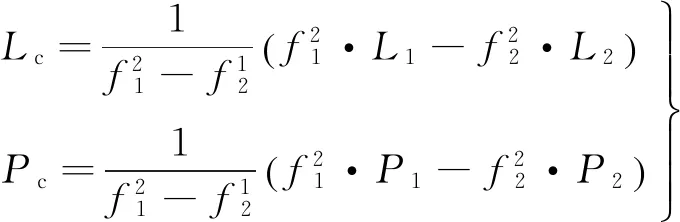
(2)

式中：Lc、Pc分别为消电离层载波相位及伪距组合观测值；f1、f2分别为双频载波频率；L、P分别为载波相位及伪距观测值。消电离层组合观测值虽消掉电离层影响；但观测噪声却放大3倍，模糊度也不再是整数：需要较长时间来固定模糊度参数。

1.2 数据预处理

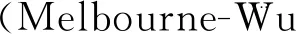
MW组合的观测方程为

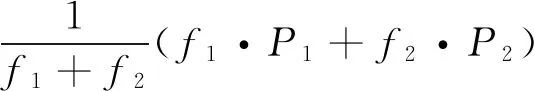
(3)

式中：Nw为宽巷模糊度；λw为宽巷波长。MW组合观测量几乎消除所有的观测误差，仅受观测噪声和多路径的影响[5]，这些影响可通过多历元观测平滑减弱或消除。若未发生周跳，Nw历元间变化很小，可通过该变化来判断当前历元是否发生周跳，详细实现方法见文献[5-6]。

电离层残差法基本公式为

(4)

式中：λ1、λ2分别为2载波的波长；N1、N2为对应的模糊度；A为与电离层电子含量相关的系数。由上式可看出电离层残差组合与接收机至卫星的几何距离无关，同时消除与频率无关的误差，仅包含电离层影响和整周模糊度与频率相关的误差[5]。若未发生周跳，电离层影响变化缓慢，适合于粗差剔除、周跳探测和修复，详细实现方法见文献[6-7]。

2 准实时精密定轨策略

本文采用的定轨软件是基于非差法的事后精密解算，无法实现实时的定轨解算。为满足轨道产品的实时应用，本文首先基于24 h弧段观测数据实现24 h弧段轨道精密解算，再进行轨道积分，外推预报24 h弧段。软件解算始终保持24 h弧段实测数据，并以此作为滑动窗口往后递推。

完成卫星精密定轨解算需要全球跟踪站观测数据，全球IGS跟踪站超过500个，若选站过多，会极大影响精密定轨解算时间，致使需预报弧段增长。本文基于均匀分布的选站原则，在全球范围共选站90个。数据处理结果显示：在选站90个情况下能在1 h内完成精密定轨解算，且实测弧段精度达到5 cm(见图2)，选用的90个跟踪站分布如图1所示。

精密定轨各颗星实测弧段精度统计如图2所示(选用2016年第100天～第106天定轨结果的均值)。

卫星精密定轨数据处理过程需进行参数控制及模型选择，本文归纳为2类：一类是与观测相关的模型、参数，这里称作观测模型；另一类是与力学相关模型、参数，这里称作力学模型。详细的观测模型及力学模型[8-10]如表1、表2所示。

表1 观测模型

本文基于滑动窗口模式的准实时精密定轨流程可描述为：经数据预处理干净后的24 h弧段观测数据，通过最小二乘批处理得到24 h实测弧段的精密轨道，通过轨道积分外推24 h轨道，由此卫星轨道一直连续向前递推。详细的数据处理流程图如3所示。

3 算例及分析

根据上一节基于滑动窗口的准实时精密定轨策略，本文选用了IGS跟踪站7 d观测数据进行准实时精密定轨。选用的跟踪站观测数据时间为2016年第100天～第106 天。精度评估标准是IGS公布的最终轨道产品，评估方式采用均方根误差(root mean square error，RMS)和标准偏差(standard deviation，STD)。

算例1：标准卫星精密轨道文件记录的是地固坐标系下的坐标，本文就3轴坐标分量随预报时长的变化趋势做了统计，限于篇幅仅给出3颗星(G01、G10、G30)3轴坐标分量趋势变化结果(其他卫星结果类似)，见图4～图6。

由上图可看出，基于滑动窗口的非差法准实时精密定轨预报弧段在第6个小时(10 800 s)后3轴偏差大于7 cm。预报弧段越长，轨道误差波动越明显，轨道精度整体呈下降趋势。

以上给出的是3轴坐标分量变化趋势，下面就卫星轨道的径向误差按每1 h统计RMS和STD，同样给出以上3颗星预报轨道径向精度变化趋势结果，如图7所示(7 d同时段累计)。

由图7可进一步得出G01、G10、G30预报轨道在6 h时轨道径向误差精度优于10 cm，预报24 h弧段轨道径向精度优于20 cm。

算例2：考虑本文精密定轨更新周期为2 h，而数据准备延迟约2 h，则用户可用精密轨道为预报弧段第4个小时后。由于本文采用2 h的轨道更新策略，故始终可为用户提供预报弧段第4至6小时弧段精密轨道。2 h更新的精密轨道对用户1 d实时可用性如图8所示。

用以上12个2 h弧段拼成24 h合成弧段，并以此评估预报第4个小时至第6个小时1 d合成弧段轨道精度。图9给出各颗卫星7 d定轨精度均值统计结果。

预报第4个小时至第6个小时1 d合成弧段7 d均值统计结果可看出：除个别卫星(G12、G16)预报精度较差外(约20 cm)，其余卫星轨道预报精度均优于15 cm；多数星轨道预报精度优于10 cm。

综上结果可看出：基于滑动窗口非差法准实时精密定轨方法的实测轨道精度优于5 cm，预报至12 h轨道精度下降至15 cm。基于2 h更新的准实时精密定轨方法的预报轨道实时可用性从预报弧段第4个小时开始。绝大多数卫星轨道预报弧段在第4个小时至第6个小时时，轨道精度优于10 cm。从时间序列及轨道精度上可看出，基于滑动窗口精密定轨方法得到的准实时精密轨道可以应用于实时精密单点定位服务中。

4 结束语

实时精密单点定位需要提供实时精密产品以削弱轨道、卫星钟差、电离层误差。由于轨道计算耗时较长，一般无法提供严格意义的实时精密轨道。若对一段弧段的精密轨道外推一段弧段，使其能覆盖当前观测时间，则可运用于实时定位服务。预报轨道精度随预报弧段增长而降低，为维持预报轨道精度需对其不断更新。本文基于定长弧段滑动更新模式的非差模型，实现了每2 h更新的准实时精密定轨，实测弧段轨道精度优于5 cm，绝大多数卫星在预报弧段第4个小时至第6个小时时的轨道精度优于10 cm，基本能做到为用户实时定位提供较高精度的准实时精密轨道产品。

致谢：感谢信息工程大学iGMAS分析中心提供的数据支持！

[1] 李征航，丁文武，李昭.GPS广播星历的轨道误差分析[J].大地测量与地球动力学，2008，28(1)：50-54.

[2] 李黎，匡翠林，朱建军，等.基于IGU预报轨道实时估计精密卫星钟差[J].大地测量与地球动力学，2011，31(2)：111-116.

[3] 赵齐乐.GPS导航星座及低轨卫星的精密定轨理论和软件研究[D].武汉：武汉大学，2004：63-64.

[4] 许国昌.GPS理论、算法与应用[M].北京：清华大学出版社，2011：106-107.

[5] 陈央央.GPS周跳探测与修复问题研究[D].西安：长安大学，2014：24-25.

[6] 陈品馨，章传银，黄昆学.用相位减伪距法和电离层残差法探测和修复周跳[J].大地测量与地球动力学，2010，30(2)：120-124.

[7] 王维,王解先,高俊强.GPS周跳探测的方法研究[J].武汉大学学报(信息科学版)，2010,35(6)：687-690.

[8] 楼益栋，施闯，葛茂荣，等.GPS卫星实时精密定轨及初步结果分析[J].武汉大学学报(信息科学版)，2008，33(8)：815-817.

[9] 李敏.多模GNSS融合精密定轨理论及其应用研究[D].武汉：武汉大学，2011：60-65.

[10]赵齐乐，刘经南，葛茂荣，等.用PANDA对GPS和CHAMP卫星精密定轨[J].大地测量与地球动力学，2005，25(2)：113-117.

Accuracy analysis on precise orbit determination based on quick updating method of arc

DAITaogao1,2，LIJianwen1,2,LIUXufang3，ZHAOJing4，JINGXin5

(1.Information Engineering University，Zhengzhou 450001，China；2.Beidou Navigation Technology Collaborative Center of Henan，Zhengzhou 450001，China；3.Troops 91650，Guangzhou 510320，China；4.Chendu University of Information Technology，Chendu 610225，China；5.Troops61363，Xi’an 710054，China)

Aiming at the problem that the satellite orbit accuracy could be lower with the longer forcasting arc in the near real-time determination of precise satellite orbiting，the paper proposed a rapidly updating method that the observing arc of 24 h was kept to improved the efficiency of updating the satellite orbit based on un-differenced model，in order to realize the near real-time determination of precise satellite orbiting.Experimental result showed that when the observing arc was sliding updated by every two hours，the accuracy of actual measured satellite orbit would be better than 5 cm；the real-time availability of forecasting satellite orbit would be delayed 4 hours；and the orbiting accuracy of compounded one day of most satellites would be better than 10 cm when forecasting at 4-6 hours，theoretically demonstrating the capability of dm-level navigation and positioning.

near real-time；precise orbit determination；sliding window algorithm；un-differenced algorithm；forecasting arc；iGMAS

2016-09-18

代桃高(1991—)，男，四川内江人，硕士研究生，研究方向为卫星精密定轨/定位的理论及应用。

代桃高，李建文，刘旭芳，等.一种弧段快速更新法的精密定轨精度分析[J].导航定位学报，2017，5(3)：28-32.(DAI Taogao，LI Jianwen,LIU Xufang，et al.Accuracy analysis on precise orbit determination based on quick updating method of arc[J].Journal of Navigation and Positioning，2017，5(3)：28-32.)

10.16547/j.cnki.10-1096.20170307.

P228

A

2095-4999(2017)03-0028-05