捷联惯导中求解圆锥误差系数的通用算法

严恭敏，杨小康，翁 浚，秦永元

(西北工业大学 自动化学院，西安 710072)

捷联惯导中求解圆锥误差系数的通用算法

严恭敏，杨小康，翁 浚，秦永元

(西北工业大学 自动化学院，西安 710072)

在捷联惯导姿态更新算法中，针对传统的由等效旋转矢量微分方程求解多子样优化圆锥误差补偿系数的推导过程比较繁琐的问题，提出了一种新的计算任意子样数优化圆锥误差补偿系数的数值算法。在圆锥角运动条件下，新算法对角速度和角增量三角函数作泰勒级数展开，再根据圆锥误差积分和不同子样角增量叉乘计算过程中的多项式系数向量叉乘特点，将叉乘运算转化为多项式系数的卷积运算，新算法易于软件编程实现。最后，通过仿真计算给出了所有共计21种1～6子样优化圆锥误差补偿系数及相应的算法漂移。

捷联姿态更新算法；优化圆锥误差补偿算法；等效旋转矢量；卷积运算；数值解

0 引言

目前，捷联惯导系统的姿态更新算法中普遍采取的思路[1]是：根据不可交换误差补偿算法，使用陀螺角增量的多子样采样构造等效旋转矢量，尽量消除转动不可交换误差，再利用等效旋转矢量计算姿态更新四元数，实现姿态更新。等效旋转矢量多子样算法的数学理论基础是等效旋转矢量微分方程(Bortz方程)[2]。由Bortz方程求解多子样不可交换误差补偿系数的方法主要有两类：一是在多项式角运动假设条件下，基于等效旋转矢量泰勒级数展开法的不可交换误差补偿系数求解[3-5]；二是在纯圆锥运动假设条件下求解的所谓优化圆锥误差补偿系数[6-7]，本文主要讨论后者。

虽然优化圆锥误差补偿系数的求解已得到了比较圆满的解决，理论上可获得任意子样系数的通式，但是它的推导过程略显繁琐[7]。本文放弃了传统的采用解析推导方法求解优化圆锥误差补偿系数的思路，在圆锥运动条件下将角速度和角增量三角函数展开成泰勒级数形式，通过仔细分析圆锥误差积分的多项式数值运算特点，给出了求解优化圆锥误差补偿系数及剩余漂移误差的通用数值算法，算法简洁，易于软件编程实现。经过仿真计算，本文给出了所有共计21种1～6子样优化圆锥误差补偿系数和漂移误差。

1 算法推导

等效旋转矢量微分方程(Bortz方程)[2]为

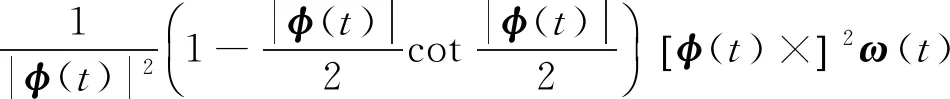
(1)

式中：t为时间参数；φ(t)、ω(t)分别表示等效旋转矢量、角速度。

式(1)在理论上严格成立，但比较复杂，不便于工程使用，通行的做法是将右端第三项视为小量，并将第二项中的等效旋转矢量近似为角增量[6-8]，从而近似有

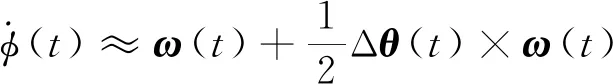
(2)

式中Δθ(t)为角增量。对式(2)右端第二项进行积分得

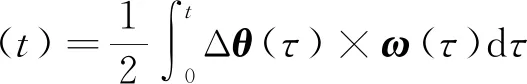
(3)

通常称δφ(t)为圆锥误差积分。

以下在圆锥运动条件下由角增量多子样采样估计圆锥误差积分，从而求解圆锥误差补偿系数。

首先，假设圆锥运动的角速度表达式为

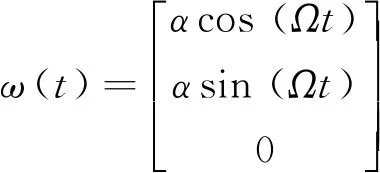
(4)

式中：α为半锥角；Ω为圆锥运动角频率。从后面推导过程中将会看到参数α和Ω均跟圆锥误差补偿系数的求解无关，所以为了书写简洁不妨把它们都作归一化处理，将角速度ω(t)展开为关于时间t的无穷级数形式，得

(5)

由式(5)积分，可得角增量

(6)

式中：Wx、Wy、Ax和Ay均为行向量，分别有：

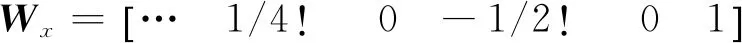
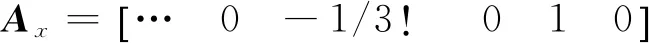
记姿态等效旋转矢量更新时间为[0,T]，根据式(5)和式(6)计算圆锥误差积分为

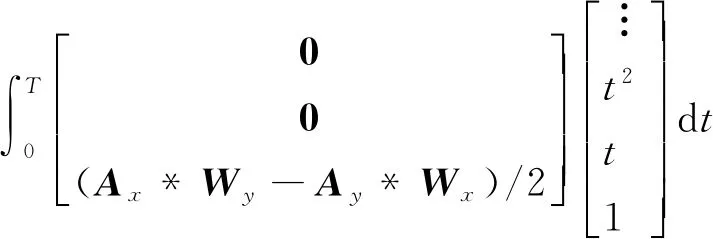
(7)

式中：运算符“*”表示两多项式系数向量之间的卷积运算。注意到，Ax和Wy的零次项系数为0、Ay的零次及一次项系数均为0，因而(Ax*Wy-Ay*Wx)/2的零次及一次项系数也为0，将其再积分后，U的零次～二次项系数均为0；再者，由于Ax和Wy(Ay和Wx)的偶(奇)次项系数均为0，因而(Ax*Wy-Ay*Wx)/2的偶次项系数也为0，将其再积分后，U的奇次项系数必为0。由上述分析可见，式(7)的z轴分量有

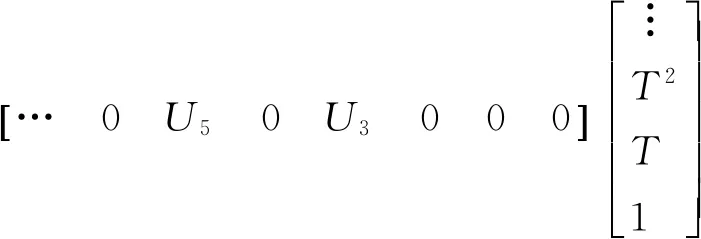
(8)

式中：Ui(i=3,5,7,…)为行向量U的非零元素。

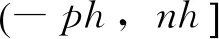
(9)

式中：有h=T/n和tj=jh，当tj>0时表示当前姿态更新周期内的角增量子样采样；而当tj≤0时表示利用了前面姿态更新周期的子样信息。

计算任意2个子样之间的叉乘积，可得

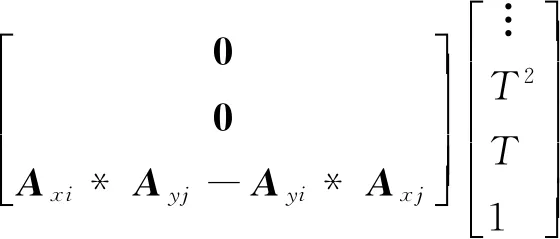
(10)

类似于式(8)对行向量U的分析，不难知道Vij的非零元素位置分布与U完全相同，则式(10)的z轴分量可写成

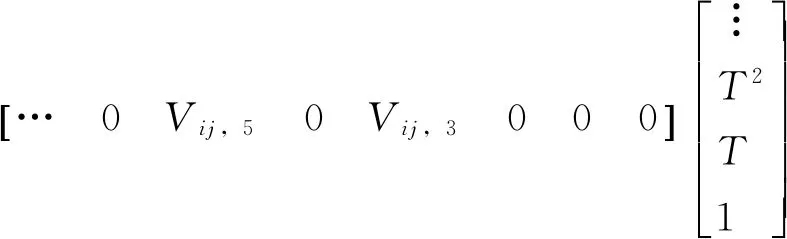
(11)

最后，对比式(8)和式(11)的行向量系数，利用N-1个子样叉乘积Δθi×Δθn(i=-p+1,-p+2,…,n-1)的线性组合对圆锥误差积分进行估计，可得系数关系式

(12)

式中kin即为N-1个待求解的优化圆锥误差补偿系数。

若令式(12)中前N-1阶非零低次项系数对应相等，可得N-1维线性方程为

(13)

如将式(13)简记为

Z=BK，

(14)

则可立即求得优化圆锥误差补偿系数

K=B-1Z。

(15)

此外，若在式(13)成立的情况下将式(12)两边第2N+1次项系数的差异定义为N子样剩余圆锥误差漂移系数ρN，则有

(16)

考虑到实际圆锥运动参数半锥角α、角频率Ω及姿态等效旋转矢量更新周期T，漂移系数ρN与以rad/s表示的圆锥误差补偿算法漂移εN之间的关系[9]为

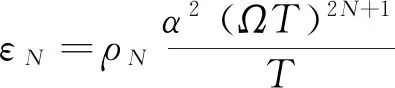
(17)

至此，完成算法推导。

2 仿真与分析

根据前一小节的公式推导，下面给出求解优化圆锥误差补偿系数的主要步骤：

1)根据式(5)和式(6)，设定角速度和角增量系数向量Wx、Wy、Ax和Ay；

2)根据式(7)计算圆锥误差积分系数向量U；

3)按需求选择子样参数n和p，根据式(9)和式(10)计算角增量子样Δθj及叉乘积系数向量Vij；

4)构造方程(13)，由式(15)～式(17)求解优化圆锥误差补偿系数kin、漂移系数ρN和算法漂移εN，完毕。

按照上述步骤，笔者编写了Matlab仿真计算程序[10]，表1列出了当N=1～6时的所有共计21种子样数的优化圆锥补偿系数及算法漂移的仿真结果，其中在计算算法漂移εN时，假设半锥角α=1°、锥频率Ω=2π rad/s且采样间隔h=0.01 s。为了表示简洁，使用Matlab的“format rat”命令将优化圆锥误差补偿系数kin和漂移系数ρN转换成分数形式，算法漂移εN仅保留了3位有效数字。表1中序号右上标未标注“*”号的结果与已有文献的结果完全一致[6-7]，而标注“*”号的结果是本文首次给出的。从表1算法漂移εN一列数据可以看出，在圆锥运动参数α、Ω和h相同的情况下，子样数N=n+p越多则算法漂移εN越小；而在子样数N一定的条件下，不论如何分配当前子样数n和以往子样数p， 都具有相同的算法漂移。显然，如果不考虑计算量的话，选择较大的N和较小的n， 有利于减小算法漂移并提高姿态更新输出频率。

表1 各子样(N=1～6)优化圆锥误差补偿系数及算法漂移

3 结束语

传统求解优化圆锥误差补偿系数的理论思路并不复杂，但公式推导过程稍显繁琐，本文通过三角函数的泰勒级数展开，采用卷积算法进行多项式向量的叉乘运算，给出求解优化圆锥误差补偿系数的方法和软件编程都非常简便，当然，读者还可根据需要任意设置子样数N(包括p和n)，运行程序后便可立即得到相应的系数，避免了繁琐的公式推导过程。最后，文中给出了共计21种1～6子样优化圆锥误差补偿系数及相应的算法漂移，为实际应用和算法选择提供了更多的参考和便利。

[1] SAVAGE P G.Strapdown inertial navigation integration algorithm design part 1：attitude algorithms[J].Journal of Guidance，Control，and Dynamics，1998，21(1)：19-28.

[2] BORTZ J E.A new mathematical formulation for strapdown inertial navigation[J].IEEE Transactions on Aerospace and Electronic Systems，1971，7(1)：61-66.

[3] MILLER R.A new strapdown attitude algorithm[J].Journal of Guidance，Control，and Dynamics，1983，6(4)：287-291.

[4] LEE J G，YOON Y J，MARK J G，et al.Extension of strapdown attitude algorithm for high-frequency base motion[J].Journal of Guidance，Control，and Dynamics，1990，13(4)：738-743.

[5] 秦永元，张士邈.捷联惯导姿态更新的四子样旋转矢量优化算法研究[J].中国惯性技术学报，2001，9(4)：1-7.

[6] IGNAGNI M B.Efficient class of optimized coning compensation algorithms[J].Journal of Guidance，Control，and Dynamics，1996，19(2)：424-429.

[7] PARK C G，KIM K J，LEE J G，et al.Formalized approach to obtaining optimal coefficients for coning algorithms[J].Journal of Guidance，Control，and Dynamics，1999，22(1)：165-168.

[8] 王立冬，孟亚峰，高庆.基于角增量和角速率的旋转矢量算法的等效性[J].宇航学报，2014，35(3)：340-344.

[9] 严恭敏，严卫生，徐德民.经典圆锥误差补偿算法中剩余误差估计的局限性研究[J].中国惯性技术学报，2008，16(4)：379-385.

[10]严恭敏.高精度捷联惯性导航系统Matlab工具箱[EB/OL].(2013-09-16) [2017-4-12].http：//blog.sina.com.cn/s/blog_40edfdc90101heg0.html.

A general numerical method to obtaining optimized coning compensationcoefficients for strapdown attitude algorithm

YANGongmin，YANGXiaokang，WENGJun，QINYongyuan

(School of Automation，Northwestern Polytechnical University，Xi’an 710072，China)

In strapdown attitude updating algorithm，the traditional deduction process from equivalent rotation vector differential equation to obtaining multi-sample optimized coning compensation coefficients is generally much cumbersome.Under the condition of coning motion，the trigonometric functions of angular velocity and angular increment are developed with the Taylor series expansion.According to coning error integral and the characteristic of polynomial coefficient vector cross production operation，contained in the process of different multi-sample angular increment cross production，the cross production is converted into convolution operation of polynomial coefficients.A new method to obtain optimized coning compensation coefficients of arbitrary multi-sample is deducted，and it is easy to implement with computer programming.Finally，a total of 21 kinds of 1～6-sample optimized coning compensation coefficients and the corresponding algorithm drift error are proposed via numerical simulation.

strapdown attitude algorithm；optimized coning compensation algorithm；equivalent rotation vector；convolution operation；numerical solution

2017-02-18

(1977—)，男，福建建瓯人，博士，副教授，研究方向为惯性导航与多源信息融合。

严恭敏，杨小康，翁浚，等.捷联惯导中求解圆锥误差系数的通用算法[J].导航定位学报，2017，5(3)：1-4,23.(YAN Gongmin，YANG Xiaokang，WENG Jun，et al.A general numerical method to obtaining optimized coning compensation coefficients for strapdown attitude algorithm[J].Journal of Navigation and Positioning，2017，5(3)：1-4,23.)

10.16547/j.cnki.10-1096.20170301.

V249.3

A

2095-4999(2017)03-0001-05