改进Smith控制与RBF单神经元PID的换热器控制系统
2017-09-11鲁广栋
鲁广栋
(辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125105)
改进Smith控制与RBF单神经元PID的换热器控制系统
鲁广栋
(辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125105)
为了高效控制工质出口温度,维持换热器稳定运行,针对Smith预估控制算法及径向基函数(RBF)神经网络辨识单神经元比例—积分—微分(PID)控制算法特点,提出了Smith控制算法和RBF神经网络辨识单神经元PID相结合的控制策略,对 Smith控制算法在结构上进行了改进,以提高RBF神经网络辨识单神经元PID控制的抗干扰能力,减少Smith控制算法对模型的依赖程度。仿真分析表明:应用于换热器工质出口温度控制系统,改进算法控制性能显著优于其它控制方法,抗干扰能力得到了大幅提高。
改进Smith控制; 径向基函数神经网络; 比例—积分—微分控制; 换热器温度控制
0 引 言
换热器是热力发电系统进行能量交换的重要设备,为了提高系统能量利用效率,维持系统高效、稳定运行,对换热器温度控制系统的研究具有重要意义[1~3]。由于换热器温度控制系统除具有容积滞后外还存在较强的时间滞后特性,被控变量不能及时反映系统所承受的扰动,调节效果具有较明显的超调量和较长的调节时间。
针对以上问题,国内外学者开展了大量研究[4~6]。Vasicˇkaninová A等人提出了将神经网络预测控制(neural network predictive control,NNPC)策略应用在换热器控制中,结果表明神经网络预测控制比常规PID控制的效果更好[7]。Kalogirou Soteris A等人将人工神经网络控制理论应用于太阳能换热器装置中,取得较好控制效果[8]。胡开明等人提出了基于Smith预估控制和组态技术的锅炉内胆温度控制,与普通比例—积分—微分(proportion-integration-differentiation,PID)控制相比控制器性能指标及系统抗干扰能力得到改进[9]。上述研究可使系统性能得到一定改善,但由于预测控制存在精度不高、滚动优化策略少、反馈校正方法单调等问题,使得预测控制的效果不理想,单独神经网络控制抗干扰能力不足,Smith控制算法对模型的依赖程度高。
针对以上问题,本文提出了一种改进的Smith预估控制与径向基函数(radial basis function,RBF)神经网络辨识单神经元PID的联合控制算法。算法利用RBF神经网络辨识单神经元PID在线辨识、在线学习、自适应的特点以及改进Smith控制算法具有抑制外界干扰,对模型依赖程度低的特点,将其应用于中低温余热温度控制系统中,对提高中低品位能源的回收利用有重要作用。
1 换热器温度系统模型
换热器作为热力发电系统的重要设备,在实际计算和控制中通常采用传递函数来描述。而换热器作为多容时滞对象,其模型阶次高,非常复杂,通常利用低阶近似方法对其进行处理。其中结构模型的建立和参数求解依据实测数据估计,其动态模型为[10]

(1)
2 改进的Smith预估控制
由于Smith预估控制[11]闭环传递函数分子上滞后环节的存在,被控量的响应要滞后设定值τ时刻;且其严重依赖于系统模型,很难得到广泛应用,因此,本文提出了改进的Smith控制算法,通过减弱其对模型的依赖程度更好地对延迟对象进行补偿,同时提高了系统的抗干扰能力,增强系统的稳定性。改进后的系统框图如图1所示。其中,d(s)为干扰信号,TS为微分运算。

图1 改进的Smith预估控制系统
改进Smith预估控制系统中,对TS的处理方式为用一系列采样时间点kT代表连续时间t,以一阶后向差分替代微分,即
(2)
3 改进Smith控制算法与RBF网络辨识单神经元PID控制
由于RBF网络辨识单神经元PID控制器抗干扰能力弱,稳定性较差,本文提出了一种将改进Smith预估控制与RBF网络辨识的单神经元PID控制相结合的控制算法,能够在一定程度上解决系统响应速度和超调的矛盾。结构如图2所示。
图2中,神经网络控制器(NNC)为单神经元PID控制器,神经网络辨识器(NNI)为RBF,协助 PID辨识被控对象的Jacobian信息。
改进Smith与RBF神经网络辨识的单神经元PID控制算法的控制过程归纳如下:

图2 改进Smith与RBF单神经元PID控制器结构
1)分别给出单神经元PID初始学习速率ηI,ηP,ηD及比例系数K和RBF网络输出层权值wj,节点中心cj,节点基宽参数bj以及学习速率和动量因子。
2)采用增量式PID控制器控制误差为
ys(k)=yout(k)-ym(k)
(3)
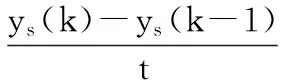
(4)
e(k)=rRin(k)-yy(k)-yx(k)
(5)
式中rRin(k)为k时刻系统;yx(k)为k时刻1回路输出信号;ym(k)为k时刻2回路输出信号;yy(k)为k时刻3回路输出信号。
3)单神经元网络的输入
(6)
4)Jacobian辨识信息
Vwj(k)=h(y(k)-ym(k)hj
(7)
wj(k)=wj(k-1)+Vwj(k)+α(wj(k-1)-
wj(k-2))
(8)

(9)
bj(k)=bj(k-1)+Vbj+α(bj(k-1)-bj(k-2))
(10)

(11)
cji(k)=cji(k-1)+Δcji(k)+α(cji(k-1)-
cji(k-2))
(12)
Jacobian矩阵算法为
(13)
式中 x1=Δu(k)。
5)加权系数的计算
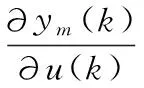
(14)
6)控制器的输出为

(15)
式中K为单神经元的比例系数;wi(k)为单神经元网络的权系数。
7)令K=K+1,返回步骤(2),进行下一次采样控制。
该算法兼顾RBF神经网络辨识的单神经元PID控制器和改进Smith控制算法的优越性能。RBF网络辨识单神经元控制器在满足系统稳定性前提下改善了响应迟滞的缺点,提高了系统响应速度;同时在误差较小范围内,精确控制。而改进Smith预估控制器在提高系统控制品质的同时,提高系统的抗扰动性能。
4 仿真研究
针对低温余热发电系统换热器出口温度控制,其传递函数如式(1),采样时间为t=5 s,RBF采用3-6-1结构,网络辨识的三个输入为:r=[Δu(k),yout(k),yout(k-1)],输出为yout(k),考虑低温余热利用系统中热源温度一般为150~180 ℃,故取系统输入的阶跃信号rin(k)=140.0,当k=90时,加入d(k)=50.0的扰动信号,在改进的Smith预估控制与RBF辨识的单神经元PID控制中η=0.5,a=0.1,ηP=0.06,ηi=0.021,ηd=0.015,K=20;在Smith预估模糊控制中kp=1.2,kd=0.8,ki=0.15;RBF网络辨识的单神经元PID控制的参数ηP=0.35,ηi=0.15,ηd=0.025,K=10,其他参数相同;在Smith预估与RBF辨识的单神经元PID控制中ηP=0.1,ηi= 0.018,ηd=0.02,K=25,其他参数与以上控制方法参数相同;为了验证本文所提算法的有效性,利用Matlab 7.0进行数值仿真。
4.1 不同控制方法系统仿真比较
仿真结果如图3所示。

图3 改进算法对系统进行控制输出波形及比较
由图3可知,在温度控制中仅仅采用常规Smith控制算法与RBF网络辨识单神经元PID控制相结合,当受到d(k)=50.0的外加干扰时,系统的抗干扰能力有所提高、但是响应速度变慢,故简单的控制器叠加组合对系统的控制性能改善作用不大。
在系统响应时间方面,改进算法 综上所述,改进算法在响应速度方面所需时间更短,在抑制外界干扰时,抖动幅度更小,恢复系统稳定更快。对控制算法的改进达到了预期效果。 4.2 系统鲁棒性验证 控制器的鲁棒性是评价其优劣的重要指标,对于改进控制算法采用Matlab进行仿真,分别将被控对象的增益延迟时间增加20 %,仿真结果如图4所示。 图4 不同控制器时,系统鲁棒性验证曲线 由图4(a),(b)可知,若系统的参数发生变化,改进算法较其他控制方法,在响应速度、抑制超调方面具有非常好的控制性能,若系统参数发生变化又加入d(k)=50.0的外界干扰时,改进算法能很好地抑制外加干扰,快速恢复系统稳定,可知,其鲁棒性能较其他控制方法十分突出。因此,在低温余热利用换热器温度控制系统中采用改进算法进行控制是比较理想的选择。 针对低温余热利用系统换热器温度控制中存在的时变性,大滞后等问题,提出了将改进Smith控制算法与RBF网络辨识单神经元PID联合控制,解决了常规Smith控制算法与RBF网络辨识的单神经元PID控制进行结合时系统响应速度慢,抑制外界扰动能力弱的问题,同时,克服了RBF网络辨识的单神经元PID控制抑制外界扰动能力差的弊端,实现了在线辨识、在线控制的目的,提高了控制系统的精度,增强了系统抑制外界扰动的能力,具有很好的动静态特性,以及较强的自适应性和鲁棒性能。 [1] 刘志远,吕剑虹.智能 PID 控制器在电厂热工过程控制中的应用前景[J].中国电机工程学报,2002,22(8):128-134. [2] Pang Z.Learning algorithm for RBF neura networks based on improvedk-means algorithm[J].Computer Engineering & Applications,2012,48(11):161-163. [3]RongPanxiang,SunJianpeng,LiuZhaoyu,etal.SimulationandresearchofboilercombustionprocessbasedontheimprovedRBFneuralnetwork[J].InternationalJournalofu-ande-Service,ScienceandTechnology,2013,6(5):79-87. [4] 韩 莉,张振宇,刘 倩,等.基于免疫遗传算法—BP神经网络的主汽温控制[J].化工自动化及仪表,2011,38(3):274-278. [5] 乔景慧.LLNFM与RBR融合的生料分解过程工况辨识模型[J].控制工程,2016,23(4):522-526. [6] 乔俊飞,李瑞祥.基于PSO-ESN神经网络的污水BOD预测[J].控制工程,2016,23(4):463-467. [7]VasicˇkaninováA,BakosˇováM,MészárosA,etal.Neuralnetworkpredictivecontrolofaheatexchanger[J].AppliedThermalEngineering,2011,31(13):2094-2100. [8]KalogirouSA,PanteliouS.Thermosiphonsolardomesticwaterheatingsystems:Long-termperformancepredictionusingartificialneuralnetworks[J].SolarEnergy,2000,69(2):163-174. [9] 胡开明,王怀平,葛远香,等.基于Smith预估控制和组态技术的锅炉内胆温度控制[J].华东理工大学学报,2014,37(3):316-320. [10] 夏 远,程大璋.基于智能控制技术在换热器控制系统中的研究[J].低压电器,2007(24):5-9. [11] 齐朝阳,郑恩让.迭代模型Smith预估控制:算法和稳定性[J].控制工程,2015,22(1):133-138. 鲁广栋(1992- ),男,硕士研究生,主要从事矿山节能理论与技术,低温余热发电系统控制策略方向的研究工作。 Heat exchanger control system based on improved Smith control and RBF single neuron PID LU Guang-dong (School of Electrical and Control Engineering,Liaoning Technical University,Huludao 125105,China) In order to control working fluid outlet temperature efficiently and maintain the stable operation of the heat exchanger,aiming at characteristics of Smith predicted control algorithm and radial basis function(RBF) neural network of single neuron PID control algorithm,control strategy combined Smith control algorithm and RBF neural network single neuron PID is proposed.Smith predicted control algorithm is improved in the structure to reduce its dependence on the model.Meanwhile,the anti-interference ability of RBF neural network PID is increased.The simulation results show that the proposed algorithm can make the control performance and the anti-interference ability significantly better than others when it is applied to temperature control system of heat exchanger. improved Smith control; radial basis function(RBF) neural network; proportion-integration-differentiation(PID)control; heat exchanger temperature control 10.13873/J.1000—9787(2017)09—0094—03 2016—10—10 TP 273 A 1000—9787(2017)09—0094—03
5 结 论
