与年龄相关的随机种群模型解的均方散逸性
2017-09-11张启敏李西宁
张启敏, 李西宁, 杨 莉
(宁夏大学数学统计学院,银川 750021)
与年龄相关的随机种群模型解的均方散逸性
张启敏*, 李西宁, 杨 莉
(宁夏大学数学统计学院,银川 750021)
讨论了一类与年龄相关的随机种群模型数值解的均方散逸性: 基于步长h受限制和无限制的2种条件, 利用倒向欧拉法和补偿的倒向欧拉法分析了该随机种群模型数值解的均方散逸性并加以证明, 结论证明补偿的倒向欧拉法更适合解决与年龄相关的随机种群模型数值解的均方散逸性问题.
随机种群模型; 倒向欧拉法; 补偿的倒向欧拉法; 均方散逸性
微分方程数值解的均方散逸性已引起了诸多学者的关注[1-9],本文考虑如下与年龄相关的随机种群模型[10]:
(1)
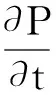
由于与年龄相关的随机种群模型的精确解很难得到,使得模型(1)的数值解十分重要. 因此,模型(1)数值方法的建立在计算数学领域中显得尤为重要. 近几年,TAN等[11]利用Split-stepθ方法讨论了模型(1)的数值收敛性;金小薇和张启敏[12]运用逐次逼近法研究了模型(1)系统解的存在性及唯一性;张彦山和张启敏[13]采用同时逼近年龄和时间的方法,探究了在固定时间内模型(1)种群数量的收敛问题;李西宁和张启敏[14]分析了模型(1)强解的存在性与唯一性;杨莉和张启敏[15]讨论了模型(1)数值解的全局稳定性. 然而关于模型(1)解的均方散逸性的研究并未见到. 因此,本文分别利用倒向欧拉法和补偿的倒向欧拉法讨论了模型(1)数值解的均方散逸性.
1 预备知识
令V=H1([0,A])≡{φ|φL2([0,A]),L2([0,A])},其中是偏导数,V是Sobolev空间,V′是V的对偶空间,H=L2[0,A]满足

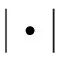
|x|≤m‖x‖,∀xV.
B(K,H)是K到H的有界线性算子,‖B‖2是Hilbert-Schmidt范数,即
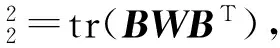
其中W是完备空间(Ω,,P)取值在可分的Hilbert空间上的Brown运动ωt的增量协方差算子. 令N(t)为强度的泊松过程,(t)∶=N(t)-t是泊松过程的补偿过程.
为了研究模型(1)数值解的均方散逸性问题,我们做出如下假设:
(i)存在常数ψ≥0,υ<0,ω≥0,η≥0,满足
(2)
(ii)模型(1)中的μ(t,a),β(t,a)满足
(3)
其中(t,a)Q,μ0和β是常数.
2 随机种群模型数值解的均方散逸性
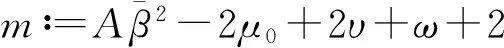
(i)对任意给定的ε>0,存在正数t*,满足

(ii)对任意给定的ε>0,模型(1)的数值解是均方散逸的,其中=(0,-2ψ/m+ε)是均方吸引集.
首先,利用倒向欧拉法讨论模型(1)数值解的均方散逸性:
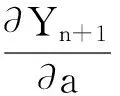
g(tn,Yn)ΔBn+h(tn,Yn)ΔNn,
(4)
其中初始值Y(0,a)=P(0,a),步长h=T/N>0,Yn表示当tn=nh时精确解P(tn,a)的近似解.ΔBn=B(tn+1)-B(tn)和ΔNn=N(tn+1)-N(tn)分别表示布朗运动的增量和泊松过程的增量.
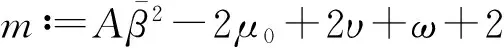
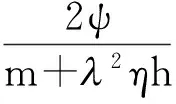
其中η>0时,h0=-m/(2η);η=0时,h0=+.
证明 根据式(4)有

|Yn+g(tn,Yn)ΔBn+h(tn,Yn)ΔNn|2.
(5)
从而有
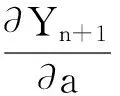
f(tn+1,Yn+1))〉+|Yn|2+|g(tn,Yn)|2|ΔBn|2+
|h(tn,Yn)|2|ΔNn|2+2〈Yn,g(tn,Yn)ΔBn〉+
2〈Yn,h(tn,Yn)ΔNn〉+2〈g(tn,Yn)ΔBn,h(tn,Yn)ΔNn〉.
(6)
由于E(ΔBn)=0,E(ΔBn)2=h,E(ΔNn)=h,E(ΔNn)2=h+2h2成立[11],则E|Yn+1|2≤E|Yn|2+hE|g(tn,Yn)|2+
(7)

(8)
则结合式(2)及式(3),推出
E|Yn+1|2≤[1+(ω+2+η)h+2ηh2]E|Yn|2+
(9)
即
[1+(ω+2+η)h+2ηh2]E|Yn|2+2ψh.
(10)
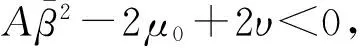
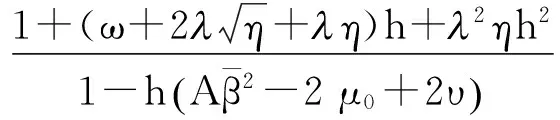

(11)
通过Cauchy-Schwarz不等式[12]有
E|Yn+1|2≤C1E|Yn|2+D1,
(12)
其中


通过递推算法推出

最后,利用补偿的倒向欧拉法讨论模型(1)数值解的均方散逸性:
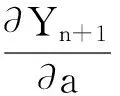
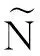
(13)

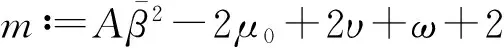

证明 根据式(2)推出
〈P(t,a), f(t,P)〉=〈P(t,a), f(t,P)〉+
(14)
类似地,由式(13)可得
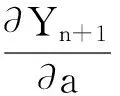
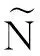
(15)

f(tn+1,Yn+1))〉+E|Yn|2+hE|g(tn,Yn)|2+
(16)
结合式(2)、(3)及式(8)可推出

2ψh[1+(ω+η)h]E|Yn|2,
(17)
即
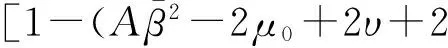
(18)


(19)
其中
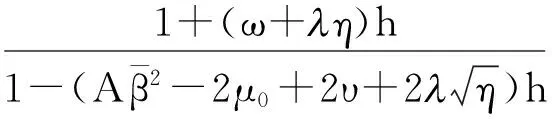

通过递推算法可知
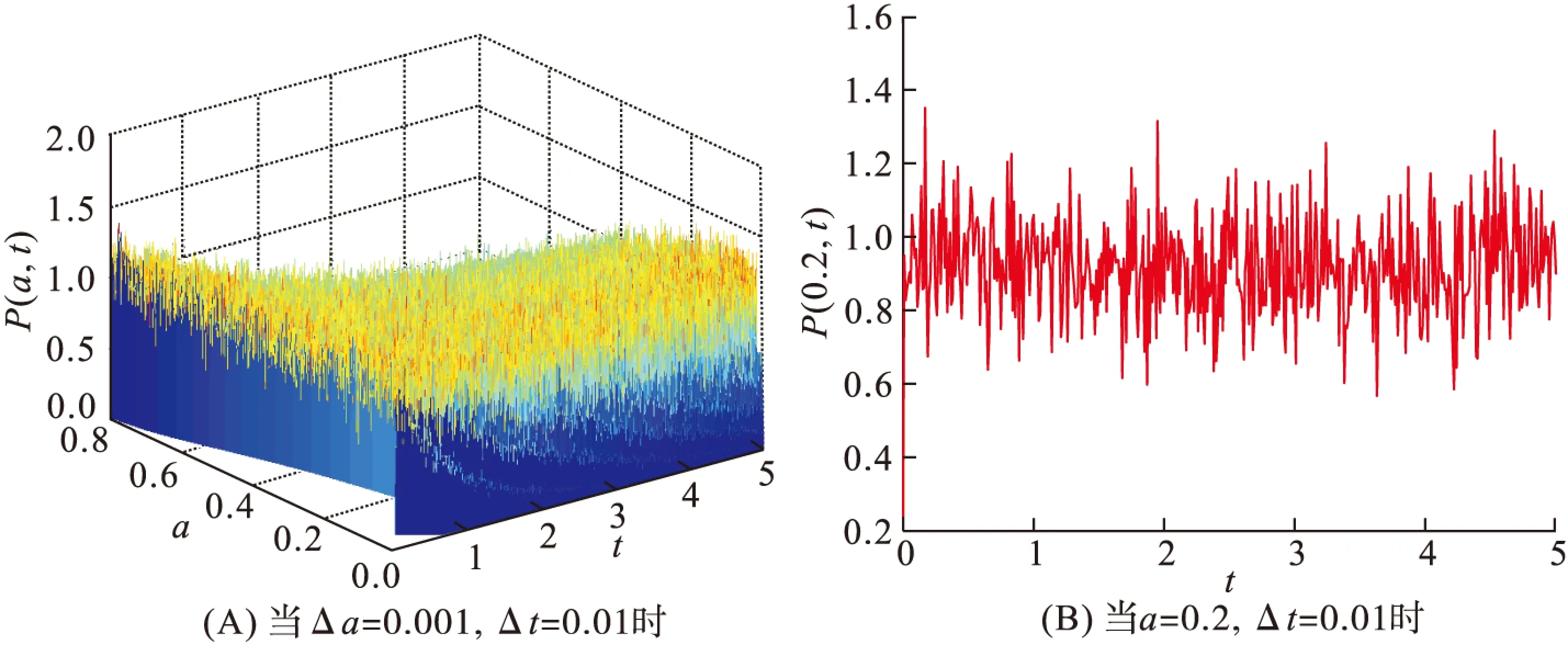
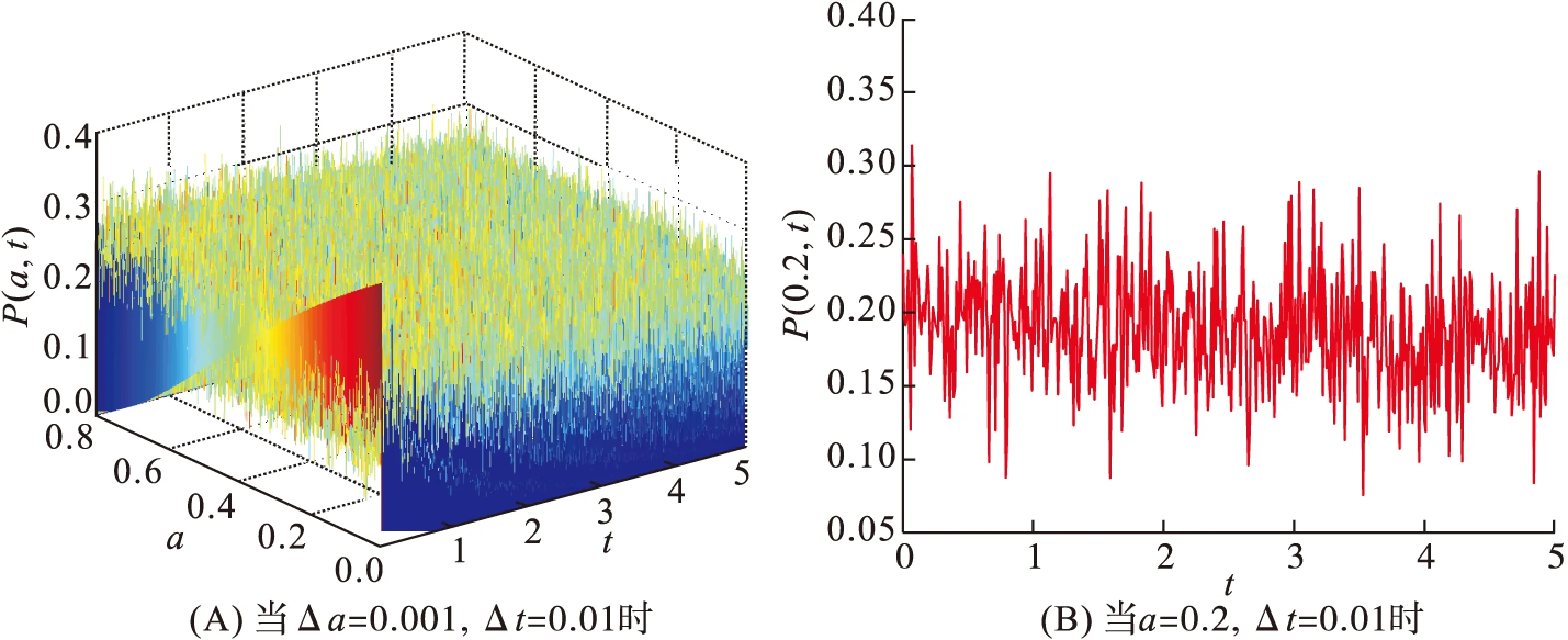
对任意的h>0有0 定理2得证. 利用下面的例子验证本文所得结论. 例1 考虑以下与年龄相关的种群模型: (20) 其中ωt是标准Brown运动,Nt是泊松过程. 图1 模型(20)的倒向欧拉法的数值模拟 图2 模型(20)的补偿的倒向欧拉法的数值模拟 本文引入了一类与年龄相关的随机种群模型系统,利用倒向欧拉法和补偿的倒向欧拉法讨论了这类与年龄相关的随机种群模型数值解的均方散逸性问题,发现倒向欧拉法适合解决步长受限制的随机种群模型数值解的均方散逸性,而补偿的倒向欧拉法适合解决步长无限制的随机种群模型数值解的均方散逸性. 因此,补偿的倒向欧拉法比倒向欧拉法更适合解决与年龄相关的随机种群模型数值解的均方散逸性问题. [1]STUARTAM,HUMPHRIESAR.Dynamicalsystemsandnumericalanalysis[M].Cambridge:CambridgeUniversityPress,1996. [2]GANS.Exactanddiscretizeddissipativityofthepantographequation[J].JournalofComputationalMathematics,2007,25:81-88. [3]GANS.Dissipativityofθ-methodsfornonlineardelaydifferentialequationsofneutraltype[J].AppliedNumericalMathematics,2009,59:1354-1365. [4]LIUX,WENL.Dissipativityofone-legmethodsforneutraldelayintegro-differentialequations[J].JournalofComputationalandAppliedMathematics,2010,235:165-173. [5]WANGL,DINGX.Dissipativityofθ-methodsforaclassofnonlinearneutraldelayintegro-differentialequations[J].InternationalJournalofComputationalMathematics,2012,89(15):2029-2046. [6]WANGLS,WANGXJ.Convergenceofthesemi-implicitEulermethodforstochasticage-dependentpopulationequationswithPoissonjumps[J].AppliedMathematicalModelling,2010,34:2034-2043. [7]RATHINASAMYA.Split-stepθ-methodsforstochasticage-dependentpopulationequationswithMarkovianswitch-ing[J].NonlinearAnalysis:RealWordApplications,2012,13:1334-1345. [8] 马婧,张启敏. 分数阶与年龄相关的随机种群系统的逼近控制[J]. 数学的实践与认识,2015,45(6):230-239. MAJ,ZHANGQM.Approximatecontrollabilityoffractionalstachasticage-dependentpopulationsystems[J].MathematicsinPracticeandTheory,2015,45(6):230-239. [9]ZHANGQM,LIUYT,LIXN.Strongconvergenceofsplit-stepbackwardEulermethodforstochasticage-dependentcapitalsystemwithMarkovianswitching[J].AppliedMathematicsandComputation,2014,235:439-453. [10]ZHANGQM,LIUWA,NIEZK.Existence,uniquenessandexpoenentialstabilityforstochasticage-dependentpopulation[J].AppliedMathematicsandComputation,2004,154:183-201. [11]TANJG,RATHINASAMYA,PEIYZ.Convergenceofthesplit-stepθ-methodforstochasticage-dependentpopulationequationswithPossionjumps[J].AppliedMathematicsandComputation,2015,254:305-317. [12] 金小薇,张启敏. 带Poisson跳的模糊随机种群扩散方程解的存在性与唯一性[J]. 华南师范大学学报(自然科学版),2014,46(4):16-21. JINXW,ZHANGQM.Existenceanduniquenessforstochasticfuzzyage-structuredpopulationequationswithdiffusionandPoissonjumps[J].JournalofSouthChinaNormalUniversity(NaturalScienceEdition),2014,46(4):16-21. [13] 张彦山,张启敏. 一类与年龄相关的种群系统的数值解[J]. 应用数学,2009,22(2):303-309. ZHANGYS,ZHANGQM.Numericalapproximateschemeforstochasticage-dependentpopulationequations[J].MathematicaApplicata,2009,22(2):303-309. [14] 李西宁,张启敏. 与年龄相关的随机种群系统强解的存在性与唯一性[J]. 宁夏大学学报(自然科学版),2007,28(3):197-201. LIXN,ZHANGQM.Existenceanduniquenessofstrongsolutionsforstochasticage-dependentpopulation[J].JournalofNingxiaUniversity(NaturalScienceEdition),2007,28(3):197-201. [15] 杨莉,张启敏. 与年龄相关的种群模型解的全局稳定性[J]. 河南师范大学学报(自然科学版),2016,44(2):9-14. YANGL,ZHANGQM.Globalstabilityofmoregeneralstochasticage-dependentpopulationmodels[J].JournalofHenanNormalUniversity(NaturalScienceEdition),2016,44(2):9-14. [16]MAQ,DINGDQ,DINGXH.Mean-squaredissipativityofseveralnumericalmethodsforstochasticdifferentialequationswithjumps[J].AppliedNumericalMathemati-cs,2014,82:44-50. 【中文责编:庄晓琼 英文审校:肖菁】 Mean-SquareDissipativityofTwoNumericalMethodsforStochasticAge-DependentPopulationEquationswithJumps ZHANGQimin*,LIXining,YANGLi (SchoolofMathematicsandStatistics,NingxiaUniversity,Yinchan750021,China) The mean-square dissipativity of the numerical solution for a class of stochastic age-dependent population equations with jumps is discussed. Based on the step length under the condition of limited and unlimited, it is essential for studying the mean-square dissipativity to use backward Euler method and compensated backward Euler method for stochastic age-dependent population equations with jumps. The results show that the compensated backward Euler method is more suitable for solving the mean-square dissipativity about stochastic age-dependent population equations with jumps. age-dependent population models; backward Euler method; compensated backward Euler method; mean-square dissipativity 2016-01-21 《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n 国家自然科学基金项目(11461053,11261043) O A 1000-5463(2017)04-0106-05 *通讯作者:张启敏,教授,Email:zhangqimin64@sina.com.

3 数值算例
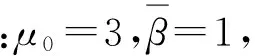
4 结论
