基于MED-Teager能量算子的滚动轴承故障诊断

刘正平，胡 俊，胡俊锋，张 龙

（华东交通大学机电与车辆工程学院，江西 南昌330013）

基于MED-Teager能量算子的滚动轴承故障诊断

刘正平，胡 俊，胡俊锋，张 龙

（华东交通大学机电与车辆工程学院，江西 南昌330013）

针对滚动轴承故障诊断中因实测信号背景噪声较大、信噪比较低，导致表征轴承故障信息的周期冲击成分被淹没于噪声中无法有效提取故障冲击特征的问题，提出一种基于MED和Teager能量算子的故障诊断模型。首先对信号最小熵解卷积（MED）处理消除采样过程中传递路径的影响；而后以Teager能量算子对滤波信号的能量值进行跟踪，从信号能量的角度进一步消除滤波信号中的带内噪声，使故障冲击特征得到二次增强；最后通过包络谱分析得到诊断结果。仿真数据及实验数据分析验证了所提诊断模型的有效性。

滚动轴承；最小熵解卷积；Teager能量算子；故障诊断

滚动轴承是旋转机械系统中最为重要的零部件，担负着传递力矩与动力的作用，由于常处于高速重载的恶劣工作环境，因此是旋转机械中的主要故障源。随着机械设备的结构复杂化日益严重，机械内部零部件的联系极为紧密，尤其对于轴承而言，一旦出现故障将引起整个机械系统的异常振动，轻则造成巨大的经济损失，重则威胁人身安全。可见，无论从经济角度还是安全角度，开展设备状态监测与故障诊断研究都显得极为必要[1-2]。

现有的故障诊断技术大多是基于振动信号的诊断，然而在数据采样过程中，受到工作环境、传递路径、多振动源相互耦合等因素的影响，实测信号往往存在较大背景噪声干扰，导致表征轴承故障信息的周期冲击成分被淹没于噪声中，这大大加剧了轴承的故障诊断难度。如何利用轴承的自身响应特性构造滤波器，将采样信号中的噪声成分去除、有效提取出故障冲击，成为提高故障诊断准确性的关键。

盲信号处理技术是信号处理领域的研究热点之一，其中，盲解卷积问题的求解作为该技术的难点问题，成为国内外学者广泛关注的主要研究方向。在此背景下，Ralph Wiggins[3]提出了最小熵解卷积（minimumentropy deconvolution,MED）的概念，用以解决盲信号处理技术中的解卷积问题的求解。该方法能够很好地消除信号中因传递路径产生的噪声成分，寻找出隐藏于背景噪声的故障分量，是滚动轴承故障诊断领域的优异算法之一[4]。冷军发等[5]将最小熵解卷积方法用于解决带式传送机传动滚动轴承早期故障难以提取的问题，并通过滤波后的包络谱分析，提取出轴承内圈点蚀故障特征。任学平等[6]考虑轴承信号受工况噪声干扰严重的问题，提出使用自回归模型消除信号中的非周期成分，而后对MED处理增强信号中的周期成分，取得了优异的故障特征提取效果。周士帅等[7]将LMD作为MED的预处理器，将信号分解成若干个PF分量后对前4个PF分量MED处理以放大故障冲击特征，成功提取出故障特征频率。上述研究虽然取得了较好的数据处理效果，但对于如何处理MED滤波后残留的带内噪声问题却未见考虑。

MED能够根据轴承故障信号的特征设计最优逆滤波器，以此消除轴承故障数据中包含的噪声分量，增强故障冲击成分的凸显状态，同时寻找出隐藏于混合信号中的故障特征信息。但对于强背景噪声下的低信噪比信号，由于噪声干扰过大，表征故障信息的异常冲击特征被淹没，MED虽然能在一定程度上消除噪声分量，但是带内噪声干扰依然严重，噪声消除效果不够理想。因此需要结合其他算法消除MED滤波后残余的带内噪声分量，以便得到更好的故障特征提取效果。Teager能量算子能够估计出信号源产生动态信号时所需的能量，从信号能量的角度增强信号的瞬态特征，特别适用于检测信号中的异常冲击成分[8]。本文提出结合MED和Teager能量算子两者的优势，期待解决MED算法带内噪声严重问题的同时为轴承故障特征提取技术的发展提供一种新思路。

1 方法介绍

1.1 最小熵解卷积

假设 x（t）为循环故障冲击成分，h（t）为传递函数，e（t）为噪声干扰成分。 则实测信号 y（t）可表示为

由于背景噪声及传递路径等因素的干扰作用，信号x（t）在逐步衰减为y（t）的过程中将失去源信号的部分特性，使熵值变大。解卷积问题便是寻找一个最优逆滤波器g（t），使输出y（t）能够恢复输入x（t）的各项特征信息。

其中，L 为逆滤波器 g（t）的长度。

在恢复输入 x（t）时，由于逆滤波器 g（t）的目的是使输出 y（t）恢复输入 x（t）的相关特征信息，因此恢复的程度越大则熵值越小。若要恢复到理想状态则其熵应取最小值，因此被称为最小熵解卷积。

由式（2）可知：

将上式写成矩阵形式：

式中：R 为 y（t）的 L×L 自相关矩阵； f=（f（l））T， f（l）的表达式：

其中：

式（6）经过迭代计算后可获得逆滤波器矩阵：

1.2 Teager能量算子

若实测信号表示为y（t），则信号y（t）的能量算子Ψ的表达式：

假设一质量为m的质量块和刚度为k的弹簧共同组成了线性无阻尼振动系统，那么，该系统的运动方程表达式：

式中：y（t）为质量块偏离平衡位置的位移量；A为振动幅值；ω为固有频率，ω=（k/m）1/2；θ为初始相位角。

振动系统处于t时刻的瞬时总能量E则为质量块动能与弹簧势能之和，即

由式（13）可得出结论：信号的瞬时总能量E与振幅A和频率ω的平方成正比。联合式（11）与式（12）：

对比式（13）与式（14）可知：振动系统的瞬时总能量E与Teager能量算子Ψ之间的差异仅为m/2（常数），由此可见，Teager能量算子Ψ能够准确跟踪振动系统的总能量E。

式（14）是对于连续时间信号的Teager能量算子的定义，而针对离散时间信号y（n），其Teager能量算子将变换为

由上式可知，若要计算出离散时间信号y（n）的Teager能量算子，仅需知晓时刻n处的3个采样点便可。由此可见，Teager能量算子对于信号中的瞬态变化十分敏感，拥有十分优异的时间分辨率。

1.3 MED-Teager能量算子故障诊断模型

考虑到MED对于强噪声干扰下的低信噪比信号特征提取效果不佳、带内噪声严重的问题，本文结合最小熵解卷积与Teager能量算子的优点，提出一种基于MED和Teager能量算子的滚动轴承故障诊断模型。诊断过程如图1所示，首先，MED根据采样信号的特征设计最优逆滤波器g（t），并对采样信号处理以初步消除采样过程中传递路径的干扰，使故障冲击特征得到一次增强；而后通过Teager能量算子计算出滤波信号的瞬时总能量E，从信号能量的角度进一步增强信号的瞬态特征，消除MED处理后残留的带内噪声；最后通过包络谱分析得到故障特征频率，与故障特征频率理论值对比以确定是否存在故障并指出故障部位。

图1 MED-Teager能量算子故障诊断模型Fig.1 MED-Teager energy operator fault diagnosis model

2 仿真数据分析

为了验证本文方法在滚动轴承故障特征提取中的有效性，根据实际工程中滚动轴承的运动状态构造出存在外圈故障的轴承仿真数据，设置采样频率为12 kHz，理论外圈故障特征频率为100 Hz，其时域波形图如图2（a）所示。图中由于仿真信号是针对轴承微弱故障，因此施加的背景噪声较大，表征着轴承故障的循环冲击特征被噪声的淹没效果较为严重，难以直观地从时域波形图中提取出故障冲击分量，因此需要对信号进行进一步操作以消除背景噪声干扰。MED根据采样信号的特征设计最优逆滤波器并对信号数据处理后的结果如图2（b）所示，其中噪声分量得到了极大程度上的消除，大部分冲击特征得到了凸显，但受到带内噪声影响，仍存在部分如300～400点处的瞬态冲击不清晰、冲击特征被掩盖等问题，因此需要进行进一步操作以增强故障信息。图2（c）为Teager能量算子对图2（b）计算后得到的系统瞬时总能量E的能量波形图，发现从系统能量的角度，隐藏于噪声中的脉冲分量能量得到了极大的增强，隐藏于图2（a）噪声中的300～400点处的故障冲击点也得以显示。包络谱中能够极为清晰地提取出故障特征频率的基频与倍频成分，其他噪声频率干扰被压制到极小范围，可见本文方法对于低信噪比信号的故障特征增强效果极为有效。

图2 仿真信号故障诊断过程Fig.2 Fault diagnosis process of simulation signal

3 实验数据分析

3.1 外圈故障

为进一步探究所提模型在故障诊断中的可行性，本节拟采用美国凯斯西储大学轴承数据中心[9]提供的实验数据进行分析。实验依托图3所示试验台，该试验台由电机、扭矩传感器、测功机和内部控制系统组成。可测试电机驱动端轴承（SKF6205-2RS轴承）及风扇端轴承（SKF6205-2RS轴承），轴承状态监测由3个加速度传感器完成，分别安装于驱动端、风机端和底座上。采用电火花技术加工不同程度的单点损伤故障以模拟现实工程中的点蚀现象。

选取故障直径0.178 mm（故障最小），安置于6点钟方向，由风机端加速度传感器采集的驱动端轴承外圈故障数据进行分析。此时采样频率为12 kHz，主轴转速 1 797 r/min，轴承参数：节径39.04 mm，滚动体直径7.94 mm，滚子个数 9，接触角0°，外圈故障特征频率为107.3 Hz。由于故障程度小且测点距离故障点较远，因此采样得到的原始振动信号图4（a）背景噪声干扰较为严重，时域波形图显得杂乱无章，极大一部分故障冲击被掩盖，从中难以提取出装载着故障信息的周期脉冲成分。运用本文所提诊断模型对该数据进行处理，图 4（b）为对图 4（a）MED 处理后的结果，经过处理后的信号消除了传递噪声干扰，信噪比明显增大，周期脉冲成分已经得到了极大的增强，能够基本判别故障脉冲点位置。运用Teager能量算子追踪信号能量，计算出系统总能量如图 4（c），相比 MED 滤波信号图 4（b），图4（c）噪声部分明显得到了极大程度的消除，而代表着轴承故障的周期脉冲成分得到了极大的增强，冲击位置极为清晰。图4（c）的包络谱图4（d）中频率噪声成分被压制到极小，提取出的包络谱故障频率也对应轴承外圈故障频率理论值，且其倍频成分十分清晰。综上所述，可判定该测试轴承存在外圈故障，结论与实际情况保持一致。可见所提模型在处理强噪声下的低信噪比信号是可行有效的，即该模型完全适用于轴承故障诊断领域。

图3 滚动轴承故障模拟实验台Fig.3 Rolling bearing fault simulation test bed

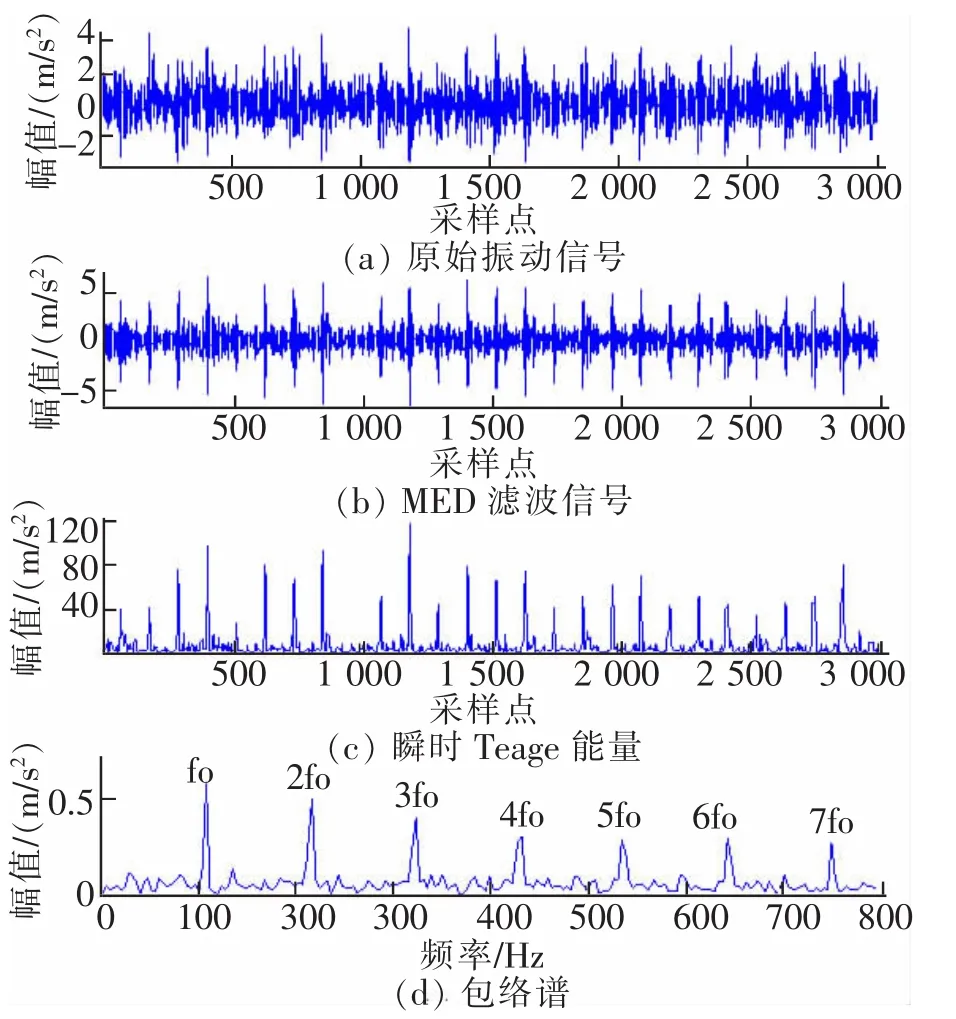
图4 外圈故障信号诊断过程Fig.4 Diagnostic process of outer ring fault

3.2 内圈故障

实验数据来源于华东交通大学检测技术与智能诊断研究所，实验平台的整体结构如图5所示，该实验平台可进行以下实验：①滚动轴承故障模拟；② 齿轮故障模拟；③轴系故障模拟。本次实验数据来源于滚动轴承故障模拟实验，测试轴承型号为N205EM型圆柱滚子轴承（轴承参数：节径38.5 mm，滚动体直径6.75 mm，滚子个数13，接触角0°），通过线切割技术在轴承的内、外圈和滚动体上分别加工不同的故障尺寸，加载装置可对驱动轴施加载荷，考虑到传感器处于不同位置时对于轴承运行状态的采样差异，分别在测试轴承座的3点钟、12点方向和底座上分别放置加速度传感器。

选取由底座加速度传感器采集、故障宽度为0.05 mm的内圈故障数据进行分析，测试时负载为0，主轴转速为1 388 r/min，采样频率为12 kHz，结合轴承参数可知内圈故障特征频率为176.73 Hz。由于故障直径为0.05 mm，程度较为轻微，且测点位置（底座）距离故障点距离较远，因此采样信号受到传递路径的干扰较大，其时域波形图6（a）中背景噪声能量较大，将携带有故障信息的循环冲击分量掩盖，仅部分冲击成分得到了展现，存在相当一部分如500，3 100，5 000，5 500数据点附近的故障脉冲隐藏于噪声，无法得到清晰体现。图6（b）中发现经过MED滤波后虽然初步去除了传递噪声干扰，于图6（a）中被噪声掩盖的故障冲击点也得以凸显，但是显然噪声消除效果不甚理想，带内噪声依然较大。对图6（b）计算估计其总能量值后，进一步消除了带内噪声，提高了信噪比，故障冲击特征已经十分明显。其包络谱的峰值频率与理论故障特征频率一一对应，且呈现出调制频带，为明显的内圈故障频率分布。因此可以判别该轴承存在严重内圈故障，与实际情况相符。

图5 旋转机械振动分析及故障诊断试验平台Fig.5 Rotating machinery vibration analysis and fault diagnosis test bed

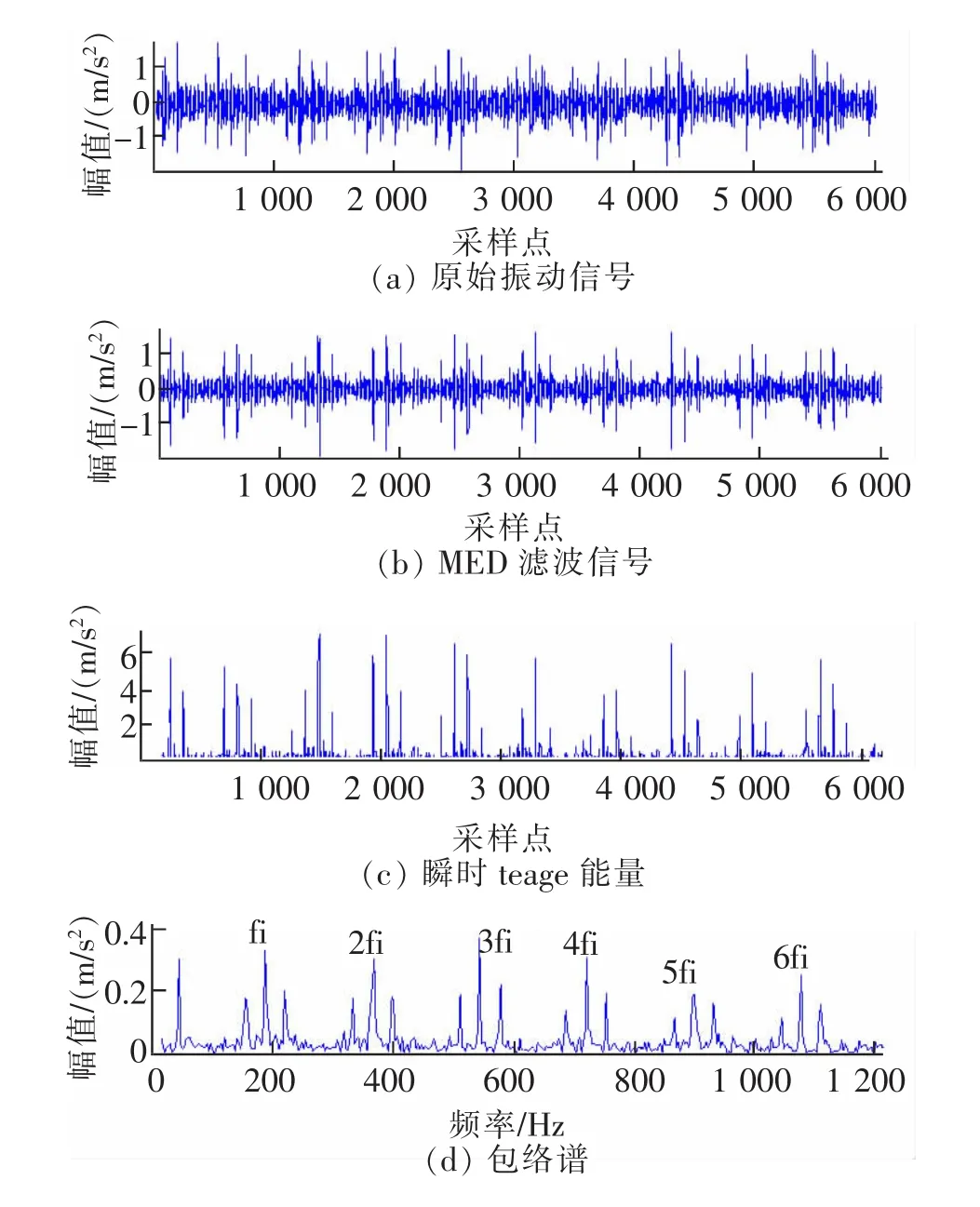
图6 内圈故障信号诊断过程Fig.6 Diagnostic process of inner ring fault

4 结束语

针对滚动轴承故障诊断中背景噪声干扰较大，无法准确提取故障脉冲信息的问题，提出MED结合Teager能量算子的方法，从信号能量的角度进一步消除带内噪声，增强故障冲击的突出效果，以此提升轴承故障诊断的准确率。本文方法的优势在于：

1）MED能够消除信号采集过程中带内噪声的影响，对于处理测点位置距离故障位置较远的采样数据具有极大的优势。

2）不以滤波的形式消除MED残存的带内噪声，而是通过Teager能量算子跟踪信号的能量值，从信号能量的角度消除带内噪声，增强故障信息的提取效果，并以信号能量作为包络线，减少了包络谱分析中的包络计算过程。

[1]陈小冬，熊国良，张磊.基于S变换和NMF的轴承故障诊断方法[J].华东交通大学学报，2016，33（5）：58-64.

[2]杨超，李亦滔.基于信号预处理和Hilbert变换的滚动轴承故障诊断[J].华东交通大学学报，2012，29（4）：1-4.

[3]WIGGINS R A.Minimum entropy deconvolution[J].Geoexploration，1978，16（1/2）：21-35.

[4]王宏超，陈进，董广明.基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J].机械工程学报，2013，49（1）：88-94.

[5]冷军发，郭松涛，荆双喜，等.基于最小熵解卷积的带式输送机传动滚筒轴承故障诊断[J].河南理工大学学报：自然科学版，2015，34（4）：514-519.

[6]任学平，张玉皓，黄培杰，等.基于自回归最小熵反褶积的滚动轴承故障诊断[J].仪表技术与传感器，2016（1）：90-92.

[7]周士帅，窦东阳，薛斌.基于LMD和MED的滚动轴承故障特征提取方法[J].农业工程学报，2016，32（23）：70-76.

[8]任达千，杨世锡，吴昭同，等.信号瞬时频率直接计算法与Hilbert变换及Teager能量法比较[J].机械工程学报，2013，49（9）：42-48.

[9]CASE WESTERN RESERVE UNIVERSITY．Bearing data center[EB/OL].2014-01-06[2017-03-26].http：//csegroups.case.edu/bearing data center/pages/welcome-case-western-reserve-university-bearing-data-center-website.

Fault Diagnosis of Rolling Bearings Based on MED-Teager Energy Operator

Liu Zhengping，Hu Jun，Hu Junfeng，Zhang Long
（School of Mechatronics&Vehicle Engineering，East China Jiaotong University，Nanchang 330013，China）

In the fault diagnosis of rolling bearings，the background noise is big and the signal noise is low,which causes a problem that the periodic impact component of bearing failure information is submerged in the noise and the fault characteristics can not be extracted effectively.Aiming at such a problem,a fault diagnosis model based on MED and Teager energy operator was proposed in this study.Firstly，the influence of transfer path was eliminated in the process of sampling by the MED method.Then the energy values of the filtered signal were tracked by Teager energy operator to further eliminate the band noise signal,which enhanced the fault impact secondarily.Finally，the diagnosis results were obtained by envelope spectrum analysis.The validity of the proposed model was verified by simulation data and experimental data analysis.

rolling bearing；minimum-entropy deconvolution；Teager energy operator；fault diagnosis

TP212

A

（责任编辑 刘棉玲）

1005-0523（2017）04-0097-07

2017－03－26

国家自然科学基金项目（51665013）；江西省青年科学基金项目（20161BAB216134）

刘正平（1963—），男，教授，硕士，研究方向为设备工程与管理，机械设备故障诊断。