北斗/GPS双模定位中快速选星算法研究

彭思博,郭承军,刘赋山

(电子科技大学 电子科学技术研究院,四川 成都 611731)

北斗/GPS双模定位中快速选星算法研究

彭思博,郭承军,刘赋山

(电子科技大学 电子科学技术研究院,四川 成都 611731)

采用双系统组合定位模式,导航接收机能在同一时刻接收到超过20颗可见星,大大增加了可见星的数量,能提供十分精准的定位。但可见星数量大幅度增加带来定位精度提升的同时也带来了大量的计算量,加上实际作业中的一些问题,都大大增加了选星时间。本文从GDOP与星座几何布局的关系出发,结合实际应用场景,提出了基于仰角和方位角排序的选星算法。该方法以满足定位要求为前提,根据可见星仰角排序初筛卫星,对不同仰角卫星进行合理的顶星选择,以卫星均匀分布为原则,将在理想情况和实际情况下寻找有效定位平衡点,以规避无效选星并减少计算量,从而大大减少选星时间,有效实现了在北斗和GPS双模定位中的快速选星。

GPS;北斗;双模定位;快速选星;仰角;方位角

0 引 言

在21世纪初,国内外的研究人员和学者对选星定位的研究主要集中于单个卫星导航定位系统。近几年,随着我国北斗导航系统的不断完善,使得北斗和GPS双模系统组合导航成为可能,相信在不久的将来,北斗和GPS以及其他系统将共同组成全球导航卫星系统(GNSS)。届时,全球导航卫星的数量将达到100颗以上,多系统组合导航中的可见星将大幅增加,系统可用性、可靠性以及定位的精度都将极大的提高[1]。但同时,在从增加的可见星中进行选择星座会产生相比单系统更大的运算量,运算量的增加带来的是时间成本的增加与实时性的降低,考虑到在一些如城市峡谷,遮挡较多的复杂环境中,最佳选星方案在实际中并不能使用,极大降低了定位的实时性。因此,在保证北斗和GPS双模导航定位精度的前提下提高定位的实时性是一个迫切需要解决的问题。本文从卫星星座几何布局与GDOP的关系出发,提出了一种适用于北斗和GPS双模定位的、实时性、适应性都较好的快速选星算法。

1 GDOP评价体系

在卫星导航定位系统中,影响定位精度的关键因素之一是几何精度因子(GDOP)[2]。在GDOP的评价体系中,由多颗卫星组成的多面体的体积大致与GDOP值成反比,该多面体所包围的空间体积越大,则GDOP值越小[3]。GDOP值的计算过程为对若干卫星观测矩阵H的伴随HT和H乘积求逆,其中H为m×m维矩阵,m为可见星数目。卫星导航定位的精度可表示为:σ=GDOP×σUERE,其中σ为定位精度的标准偏差,σUERE为用户等效距离的标准偏差。GDOP展开为

(1)

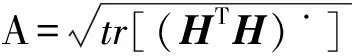
2 常用选星算法分析

2.1 最大矢端四面体体积法

最大矢端四面体体积法的理论依据是依据由星座内卫星所组成的多面体体积越大时,该星座组合的GDOP值越小,定位精度也就越高。该方法是从所有接收的卫星中选取四颗卫星的组合,计算由用户接收机与这四颗卫星所组成矢端四面体的体积。遍历所有四颗星的星座组合,然后从中选取构成星座体积最大的一组卫星来进行用户接收机位置的解算。同最佳几何误差因子法类似,虽然运算复杂度相对于最佳几何误差因子法相比略有下降,但在逻辑上也是釆用適历的方法对所有可见卫星进行次求体积的运算,运算量仍然较大,在可见卫星较多的情况下,运算量也很大,同样也会影响到用户接收机位置解算的实时性。另一方面,当卫星定位可见卫星数目大于5颗时,需要变换体积求解公式,对解算带来不便[4]。

2.2 最佳几何误差因子法

最佳几何误差因子法的原理主要是依据GDOP的值的定义,在所有可见星中,依据所要求的星座内观测卫星数目,依此遍历所有星座组合,计算出其相应的几何精度因子,然后再进行比较,为了得到定位精度更高的一组星座组合,从中选取值最低的一组来完成双模定位运算。这种方法完成的质量较高,可以获取DOP值最低的一个星座组合,但在可见卫星数目较多时,这种方法效率太低,占用时间较长,严重影响定位导航的实时性。

2.3 基于仰角的选星算法

仰角,是指用户所在位置到卫星位置的矢量在过用户所在位置的地球椭球切面上的投影与该矢量的夹角[1]。高仰角的卫星很容易被接收机捕获并跟踪,而低仰角的卫星相对要难很多。由此产生了一种基于仰角的选星算法。它通过设定仰角阈值来减少对低仰角卫星的无效选星,这极大的缩短了选星时间,能有效实现快速选星[5]。

3 基于仰角和方位角的选星算法

3.1 选星算法执行步骤

选星的第一步,便是对所有可见星的高度角以及方位角进行计算,获取的计算结果,针对其卫星系统来源对其进行区分。然后获取构成选用星座组合构成的底座星,设定遮蔽角为5°,将所有接收到的可见观测卫星分为两组,高度角为5°到60°的设为一组,高度角为60°到90°的设为另一组,分别分为低仰角组和高仰角组。在高仰角组中进行排序,选取仰角值最大的一颗星作为顶星。

在低仰角组中对方位角值进行排序。根据排序结果用方位角最大值减去方位角最小值然后除以4。得到方位角区间长度和4个方位角区间。再在低仰角组中找出4颗卫星,让他们的方位角值能够和4个方位角区间对号入座。此时,基本能够满足底座星的最均匀分布,完成了满足最优几何分布的局部最优星座分布,如图1所示。

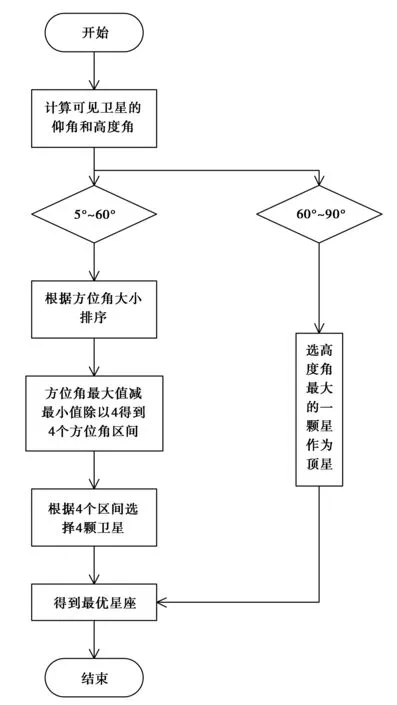
图1 快速选星算法流程图

3.2 选星算法性能分析

衡量一个选星算法的性能一般主要从算法的有效性、星座GDOP、运算量以及对后续导航定位运算的影响这几方面来考虑[6]。

1) 算法的有效性

该算法是以卫星星座几何布局与GDOP关系为依据进行设计的,该算法目标明确,流程简洁。统计分析表明,该方法能在不超过3次GDOP求解的情形下以不小于96%的概率获得GDOP小于等于6的要求。

2)GDOP值

该选星算法是以GDOP限制要求为前提来进行选星的,虽然最终所选星座的GDOP值不是最优的,但已经满足导航定位的需要,是符合要求的解。

3) 运算量

相比传统选星算法,该选星算法的计算量大大减少,在GDOP限制为6时,96%以上的选星时刻只需不超过三次GDOP计算,而所获得的GDOP均能满足导航定位要求。从总选星计算量来看,基于仰角和方位角选星算法不到传统选星算法的1%,这为北斗和GPS双模定位中实时定位提供了保证。

3.3 选星算法仿真分析

使用来自于IGS观测站北京站(BJFS站)的数据对以GPS和BD组成的双系统进行进行仿真分析。仿真时长为24 h,仿真结果如图2所示。图2为BJFS站选星前后卫星数对比图,由图2可见,选星后用于定位的卫星数远远少于选星前的可见卫星数,这极大的降低了接收机数据处理负担,有利于实现导航接收机快速实时定位。同时,当前卫星数也满足故障检测与排除要求。图3示出了选星后的GDOP曲线,由图可见,选星后,各时刻GDOP值较小,大部分都在5.5以下。一般,卫星系统可用性的选择规定为位置精度因子PDOP≤6[3],因此,采用基于仰角和方位角的选星结果是能满足导航定位要求的。图4示出了BJFS站各选星时刻采用有效仰角阈值自适应分阶选星算法进行选星求解时GDOP计算次数。从计算量来看,本文提出的选星算法在保证了GDOP值符合定位要求的同时大大减少了运算量,使得运算量相较于传统选星算法有了很大的提升。图5示出了采用传统选星算法各时刻GDOP计算次数,通过对比图4与图5可知本文所述基于仰角和方位角选星算法的计算量远远小于传统选星算法,所选卫星数能满足接收机自主完好性检测要求,所获得的星座GDOP也能满足导航定位的需要,是一种实时性良好的选星算法。

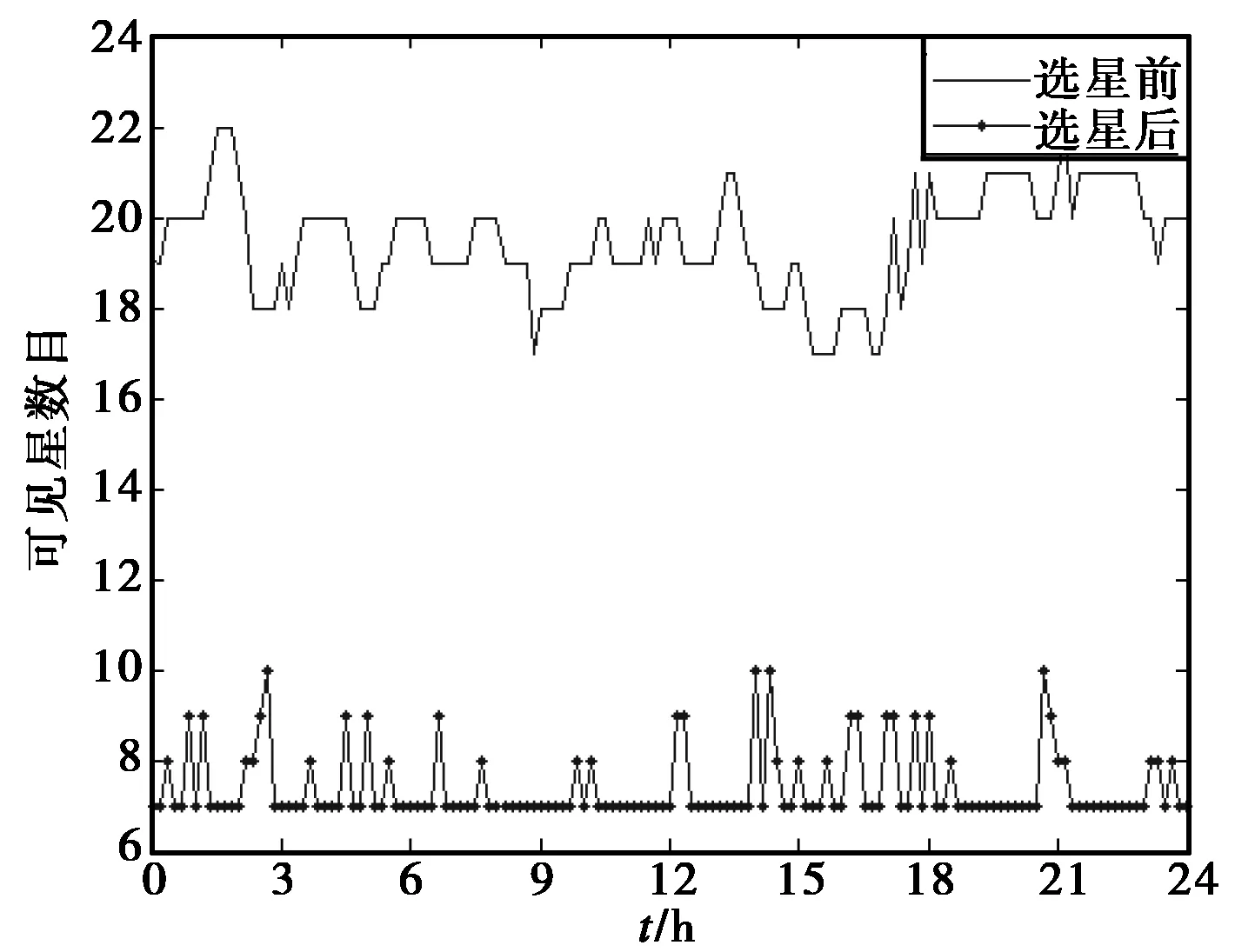
图2 选星前后卫星数对比图

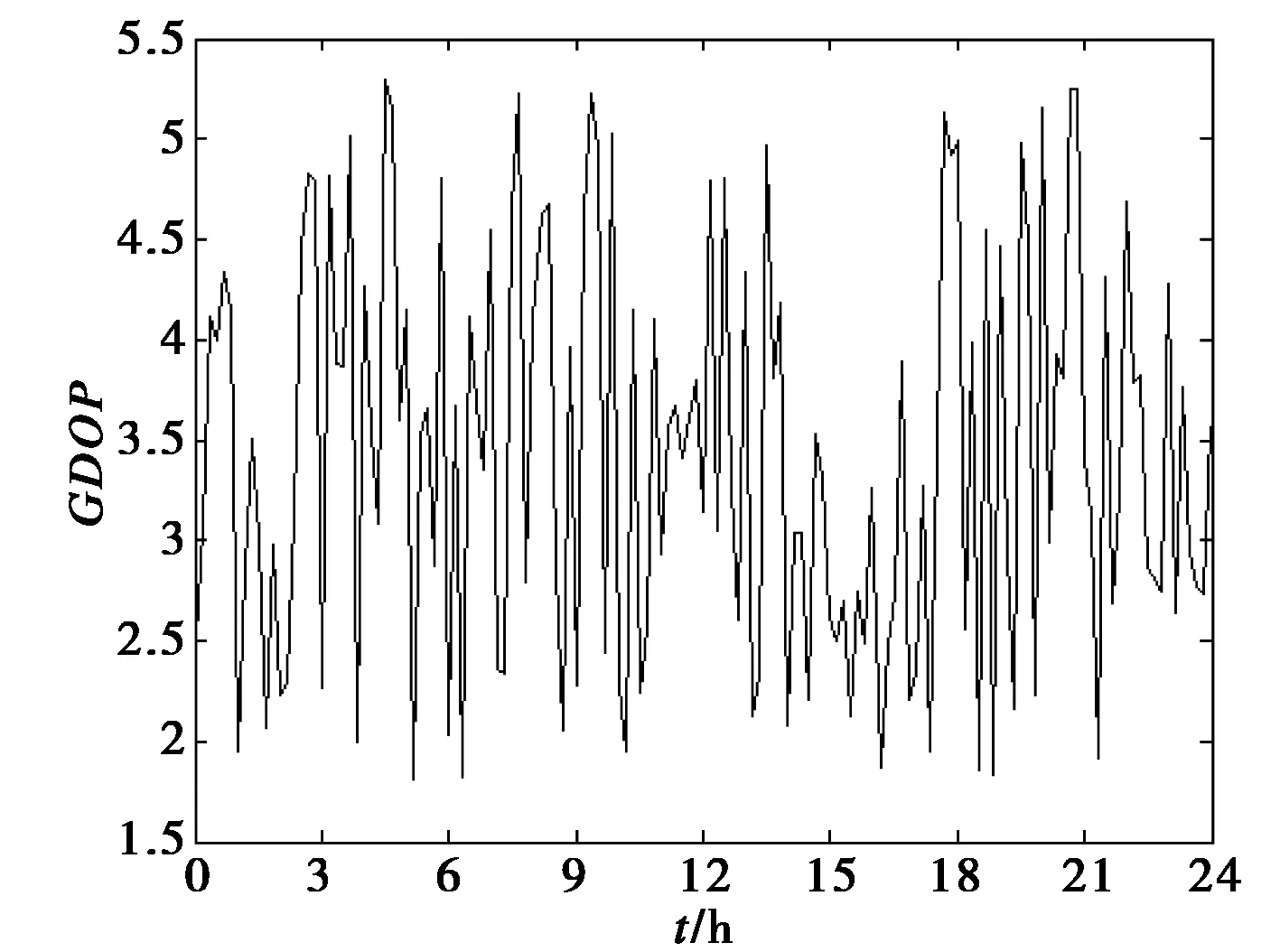
图3 各时刻选星后的GDOP值

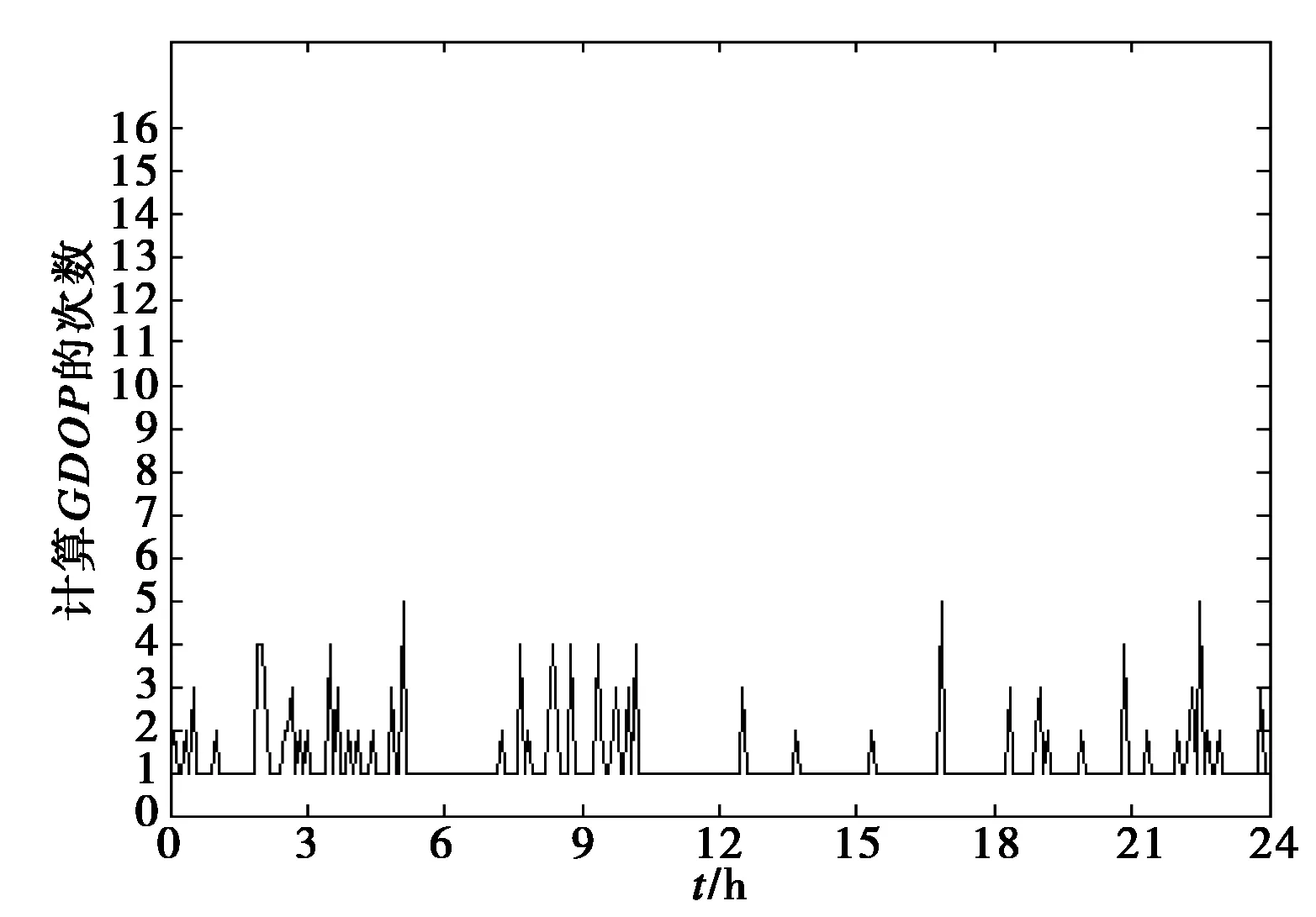
图4 各选星时刻GDOP的计算次数

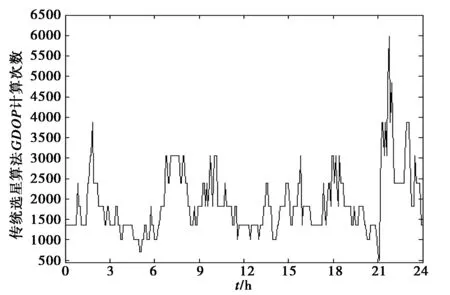
图5 各选星时刻传统选星算法GDOP的计算次数

4 结束语

本文以实现北斗和GPS双模定位快速选星为目的,从卫星星座几何布局的角度出发以获得满足设计要求的GDOP而非最优GDOP为前提,以卫星均匀分布为原则,仿真并实现了基于仰角和方位角的选星算法,详细讨论了其具体实施步骤,探讨了实际运行中的相关参数配置原则。仿真结果表明,该方法既能获得满足导航定位要求的GDOP值又克服了传统选星方法计算量大的缺点,该方法的计算量仅是传统选星算法计算量的1%左右,完全可以实现简单、快速选星并有效应用于组合定位中的实时选星。

[1] BRAFF R. Integrated GNSS/ALTIMETER landing system[C]//IONGNSS 20 the International Technical Meeting of the Satellite Division Fort Worth: The Institute of Navigation, 2007:2034-2949.

[2] KAPLA E D,HEGARTY C J. Urlde-rstanding GPS:Principles and application [M].2 ed.Beijing:Publishing House of Electronics Industry,2007:240-268.

[3] 丛丽,ABIDAT A I,谈展中,eta1.Analysis and simulation of the GDOP of satellite navigation[J].Acta Electronica Sinica,2006,34(12):2204-2208.

[4] 陈浩,范胜林,刘建业. GPS/Galileo组合导航定位系统中的选星算法[J]. 弹箭与制导学报,2009,29(4):13-15.

[5] 张强,张晓林,李宏伟,等.组合卫星接收机中的选星算法[J].北京航空航天大学学报,2007,33(12):1424-1427.

[6] KIHARA M, OKADA T. A satellite selection method and accuracy for the global positioning system[J]. Journal of the institute of Navigation, 2005:827-839.

Study on the Algorithm of Quick Select Satellite in Beidou/GPS Dual-mode Positioning

PENG Sibo,GUO Chengjun,LIU Fushan

(UniversityofElectronicScienceandTechnologyofChina,ResearchInstituteofElectronicScienceandTechnology,Chengdu611731,China)

With the continuous development of satellite navigation, following the US government first realized the GPS global positioning system, China has also developed independent intellectual property rights of the Beidou navigation system.The emergence of different satellite navigation systems makes it possible to use dual-system integrated navigation and positioning.Using a dual system combination positioning mode, the navigation receiver can receive more than 20 visible stars at the same time, which greatly increases the number of visible stars, providing a very precise positioning.But the number of visible satellites increased significantly to bring positioning accuracy at the same time also brought a lot of calculation, coupled with the actual operation of some of the problems, have greatly increased the election time.Based on the relationship between GDOP and constellation geometric layout, this paper proposes a satellites selection algorithm based on elevation and azimuth.The method is based on the requirement of positioning and filter based on the elevation of visible satellite, reasonable choice of different elevation satellites, follow the principle of uniform satellite distribution, will be find an effective positioning balance in the ideal situation and the actual situation, to avoid the ineffective selection of satellites and reduce the amount of computation, thus greatly reducing the satellite selection time.This method effectively achieved quick selecting satellite in Beidou/GPS Dual-mode Positioning

GPS; BeiDou; dual-mode positioning; rapid satellite selection; elevation angle; azimuth

10.13442/j.gnss.1008-9268.2017.03.003

2017-03-07

P228.4

A

1008-9268(2017)03-0011-04

彭思博 (1991-)，男,硕士研究生,研究方向为电子通信工程(卫星导航)。

郭承军 (1985-)，男,博士研究生,研究方向为GNSS互换性与泛位置服务、新时空体系、完好性及增强系统。

刘赋山 (1992-)，男,硕士研究生,研究方向为电子通信工程(卫星导航)。

联系人: 彭思博 E-mail: 18908096363@sina.cn