基于循环相关函数的北斗卫星导航抗干扰算法

李利军,黄际彦,刘征

(1.中国铁建电气化局集团第二工程有限公司,山西 太原 030023;2.电子科技大学,四川 成都 610054)

基于循环相关函数的北斗卫星导航抗干扰算法

李利军1,黄际彦2,刘征2

(1.中国铁建电气化局集团第二工程有限公司,山西 太原 030023;2.电子科技大学,四川 成都 610054)

当前国内外卫星导航信号空域抗干扰技术,或者需要信号到达角(DOA)信息,或者需要参考信号先验信息,或者会对导航信号和干扰同时抑制,无法形成最优的输出信干噪比(SINR),或者仅对白噪声干扰有效,无法抑制人造干扰。针对上述问题,本文提出了基于循环平稳特性的北斗抗干扰盲波束形成新算法。本文首先分析了人造干扰和北斗信号的循环平稳特性,基于此分析构造了新的盲波束形成算法的代价函数,并采用了拉格朗日方法推导了算法的解。该方法无需DOA和参考信号先验信息,可以形成阵列增益,得到最优输出SINR,可以同时抑制宽带白噪声干扰和人造调制干扰。理论分析和仿真结果证明了该方法的有效性。

北斗卫星导航系统;人造干扰;循环平稳特性;输出信干噪比

0 引 言

北斗卫星导航系统(GNSS)与美国的GPS、俄罗斯的GLONASS、欧盟的Galileo系统组成了全球四大卫星导航系统,是中国独立研发、自主运行的卫星导航系统[1-2]。北斗卫星导航系统作为一种无线电导航定位系统,在设计之初并未重点考虑抗干扰性能,不可避免的具有易受电磁干扰的特性。导航卫星信号的发射功率和接收信噪比低,接收机跟踪环路易失锁等特点使得干扰一方很容易对卫星信号进行有意的针对性的欺骗和干扰。研究表明,正常接收条件下卫星接收机天线的信噪比低于-20 dB.因此,使用一个很小功率的干扰源即可大范围内的使得卫星接收机不能正常工作。由此可见,北斗卫星导航系统的脆弱性会对经济与军事利益产生巨大的损害,发展抗干扰技术的意义重大[2-3]。

就卫星接收机抗干扰技术而言,主要分为时-频域滤波技术[4-5]和空域滤波技术[6-8]。时-频域滤波技术只能处理窄带干扰,对宽带干扰、欺骗式干扰、多径和伪卫星的远近效应效果不佳,因此发展了空时域联合滤波技术。基于波束形成的空域滤波技术是目前导航信号抗干扰技术的主要研究方向。传统的导航信号空域抗干扰技术主要分为三类:一是MVDR类算法[6]。该类算法需要知道卫星信号的DOA信息,该信息在实际环境中较难获得,对阵列误差敏感;二是MMSE、LMS和RLS等算法[7]。该类算法依靠锁相环捕获的导航信号作为参考信号,然而在干扰环境中,锁相环无法捕获到参考信号;三是功率倒置算法[8-9],该算法无需DOA和参考信号信息,但只能抑制干扰,无法形成信号阵列增益。

为了在无先验信息情况下,抑制干扰,同时得到阵列增益,研究人员发展了基于卫星信号周期平稳特性的OCAB盲波束形成算法[10]。尽管该算法能够有效抑制宽带白噪声干扰,然而其未考虑人造调制干扰与卫星信号具有相同的周期平稳特性,在人造干扰环境中,性能不佳。

针对上述问题,本文提出了基于循环平稳特性的北斗抗干扰盲波束形成算法。该方法无需DOA和参考信号先验信息,可以形成阵列增益,形成最优输出SINR,可以同时抑制宽带白噪声干扰和人造干扰。本文首先分析了人造干扰和北斗卫星信号的循环平稳特性,指出OCAB算法中的周期平稳特性是循环平稳特性的一个特例,并证明了人造干扰和卫星信号具备相同的周期平稳特性和不同的循环频率。这也是OCAB算法在人造干扰条件下失效的主要原因。基于循环平稳特性的分析,本文构造了新的盲波束形成算法的代价函数,并采用了拉格朗日方法推导了算法的解。仿真结果验证了本文算法的有效性。

1 基于多天线阵列的北斗信号模型

北斗二代卫星导航系统采用码分多址(CDMA)的多载波卫星导航系统,提供了多种的导航信号以满足不同用户的需求。北斗二代信号包括B1、B2和B3三个频点的信号,每个频点信号都是由I、Q两个支路的“测距码+导航电文+载波”构成。测距码分I支路的普通测距码(C码)和Q支路精密测距码(P码)。本文以B3频点的I支路为例说明,本文算法可直接扩展到其他频点的I、Q支路。B3频点I支路输出信号为:

S(t)=AICIDI(t)cos(2πf0t+φ) ,

(1)

式中:下角标I表示I支路;A为信号振幅;C为测距码;D为测距码上调制的数据码;f0为载波频率;Φ为载波初相。空域滤波技术采用多天线阵列进行卫星导航抗干扰处理。假设共有M个阵元,第一个阵元位置为(0,0,0),第i个阵元位置为(xi,yi,zi),卫星信号S(n)的方位角和俯仰角为(θd,φd),共有N个干扰,第j个干扰Ij(n)的来波方向为(θj,φj),则天线阵列接收信号可建模为

(2)

式中:n(n)为测量噪声;ad和aj分别为卫星信号和干扰的阵列流型。

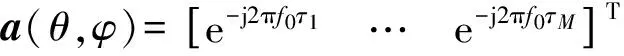
(3)

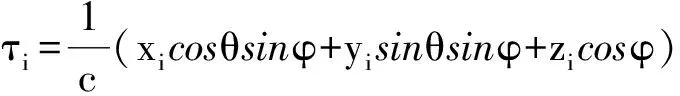
式中,c为电波传播速度。空域波束形成的目的就是找到每个阵元的权值,在阵列输出端进行加权叠加,从而在期望信号方向形成波束,在干扰处形成零陷,其阵列输出信号为

y(n)=wHx(n),

(4)

2 基于周期平稳的OCAB盲波束形成算法

为了在无先验信息情况下,抑制干扰,同时得到阵列增益,研究人员发展了基于卫星信号周期平稳特性的OCAB盲波束形成算法,并运用在GPS卫星系统抗干扰中。GPS和北斗信号结构形式类似,由式(1)可知,卫星信号由数据码、扩频码和载波组成,图1示出了C码的结构图。

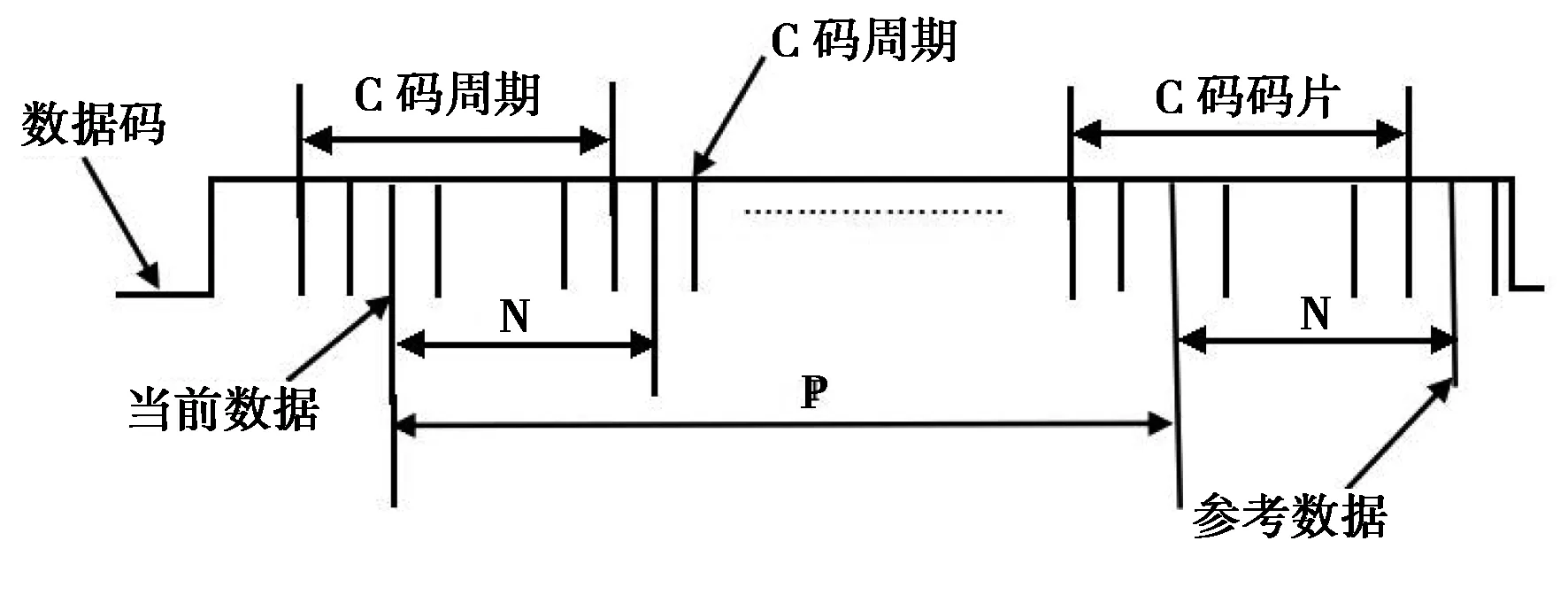
图1 卫星信号结构

由图1可知,一个卫星信号的数据码包含多个周期的C码(测距码)。设当前处理码片为S(n),参考码片为S(n-L),其中L为C码周期的整数倍。如果当前处理码片与参考码片同属于一个数据码,S(n)与S(n-L)将完全是相同的信号,这就是C码的周期平稳特性。OCAB算法首先构造它们的互协方差矩阵[10]:

Rxxl=E{x(n)x(n-L)H}

(5)

其中,Rs=E[S(n)S(n-L)H];Rj=E[Ij(n)Ij(n-L)H];Rn=E[n(n)n(n-L)H]=0.

明显的,由于L为C码周期的整数倍,Rs是相干积累可以得到最大互相关值,而此时Rn=0.OCAB算法利用上述周期平稳特性构造代价函数[10]:

(6)

式中:w为波束形成要求解的阵列权向量;Rxx=E{x(n)x(n)H}。该代价函数的目的是利用GPS信号的周期平稳特性得到卫星信号的最大增益,同时抑制干扰Ij(n)和噪声n(n)。

3 基于循环平稳特性的北斗抗干扰盲波束形成新算法

3.1 北斗信号循环平稳特性分析

尽管OCAB算法利用了卫星信号的周期平稳特性对卫星信号进行了相干积累,得到了最大的阵列增益,同时又最小化了噪声,然而其未考虑大多数人造干扰的周期平稳特性,在存在人造干扰情况下,性能恶化。若干扰是宽带白噪声干扰,此时干扰Ij(n)与Ij(n-L)相互独立,且均值为0,则

Rj=E[Ij(n)Ij(n-L)H]

=E[Ij(n)]E[Ij(n-L)H]=0.

(7)

此时,OCAB算法性能最优。若存在人造干扰时,Rj≠0,即意味着人造干扰与卫星信号具备相同的周期平稳特性,采用基于公式(6)的OCAB算法将会同时将人造干扰最大化,从而导致算法失效。下面以调幅干扰(AM)的循环平稳特性为例,说明上述结论。考虑实随机AM干扰:

x(t) =a(t)cos(2πf0t+θ)

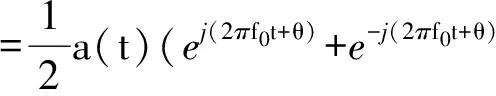
(8)

信号的循环平稳特性可由循环平稳相关函数描述:

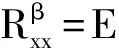
(9)

式中:τ为循环周期;β为循环频率。对比式(5)和式(9)可知OCAB算法的周期平稳特性是循环平稳特性当循环频率β为零时的特例。

由于式(8)中a(t)为实平稳信号,则有[11]:

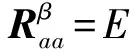
β≠0

(10)

将式(8)和式(10)代入式(9),可得实随机AM干扰的循环相关函数:

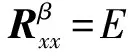
(11)

从上式中可知,对于AM干扰来说,当循环频率β=0时,式(5)中的Rj≠0.对于其他形式的调制干扰来说,采用相同的分析方法可以得到相似的结论。这也说明了人造干扰与卫星信号具备相同的周期平稳特性,采用基于公式(5)和(6)的OCAB算法将会同时将人造干扰最大化,从而导致算法失效。

采用相同的方法也可以证明卫星信号也具备循环平稳特性,其循环相关函数为

(12)

式中:ε为C码的码率,对于北斗二代B3频点来说ε=10.23 MHz.图2为北斗二代卫星基带信号与其自身的循环相关函数图和单频干扰与其自身的循环相关函数图。图中单频干扰定义为cos(2πf0t),f0=3.5 MHz.

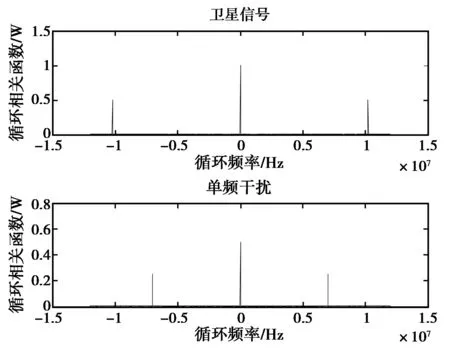
图2 北斗信号与单频干扰环相关函数

从图中可知,卫星信号与单频干扰的周期平稳特性(β=0)一致,基于周期平稳特性的OCAB对人造干扰无效。但是卫星信号与单频干扰循环频率不一样,因此采用循环相关函数可以抑制大部分人造干扰。

3.2 基于循环平稳特性的北斗抗干扰盲波束形成算法

基于上述分析,本文提出了基于循环平稳特性的北斗抗干扰盲波束形成新算法。首先重构代价函数

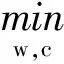
(13)

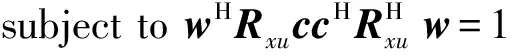
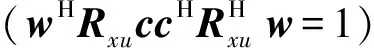
采用拉格朗日方法,上述代价函数变为

J(w,c)=wHRxxw+cHRuuc-

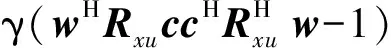
(14)

其中,γ为拉格朗日参数。令wJ(w,c)=0和cJ(w,c)=0,最小化J(w,c),得:

(15)

由上式可解得:

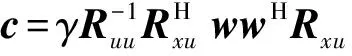
(16)

将式(16)代入式(15),可得:

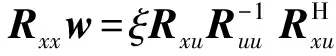
(17)

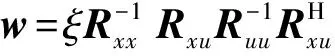
(18)

由上式可知,加权矩阵w的解为以下矩阵最大奇异值所对应的奇异矢量:

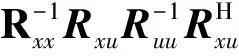
(19)

将加权矩阵w代入y(k)=wHx(k)中,即可将卫星信号S(k)提取出来。由上述代价函数和求解过程中可知,盲波束形成技术实际上就是利用了卫星信号在L和β处的循环对称相关矩阵Rss(β,L)不为0,而干扰信号和噪声在τ和α处的循环对称相关矩阵为0的特性，如图2所示,最大化卫星信号,而最小化干扰信号和噪声。

在求解滤波器权值w时,需要求解协方差阵Rxx、Rxu和Ruu,由于实际应用和仿真中,它们可以采用多个采样点信号的估计矩阵,对于具有N个采样点信号组成的数据块xN和参考数据块uN有:

(20)

由于数据码的存在,数据块可能受数据码的跳变影响。当输入信号数据块或者参考数据块被数据码跳变点隔开,则在协方差阵估计过程中可能会使部分数据被抵消掉,引起估计值的不准确,对于该问题,可采用文献[10]中的滑动平均方法解决。

4 仿真结果

参考北斗二代B3频点参数对仿真环境进行设置,参数如表1所示。

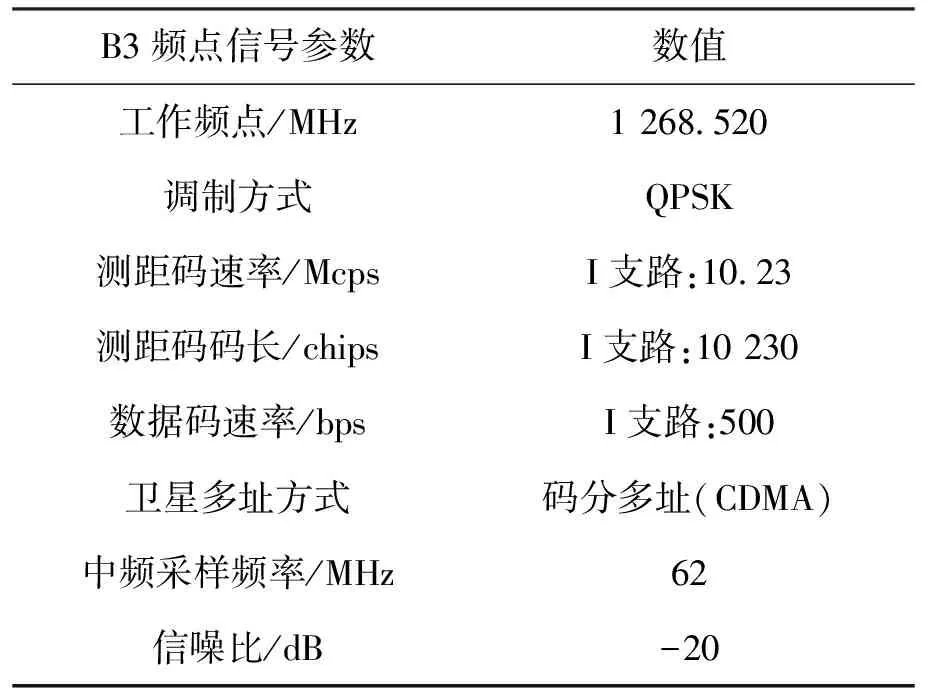
表1 北斗二代B3频点仿真参数

仿真中,MVDR算法[6]、OCAB算法[10]及功率倒置算法[8]都将与本文算法进行比较。OCAB算法、功率倒置算法和本文算法都属于盲波束形成算法,无需知道卫星信号到达角的先验信息。而MVDR算法需要知道卫星信号到达角的先验信息,当该先验信息无误差时性能最优,而存在误差时,性能恶化。多天线阵列采用9天线圆阵。卫星到达方位角和俯仰角为(240°,50°),干扰方向为(40°,75°)。干扰类型分别建模为宽带白噪声干扰、宽带扫频干扰和单频干扰。图3示出了不同宽带白噪声干扰下的输出信干噪比(SINR),从图中可以看出,OCAB、本文算法和MVDR算法的SINR高于功率倒置算法。这是因为功率倒置算法只能抑制强干扰,无法形成阵列增益。另外OCAB、本文算法和MVDR算法的性能一致,说明了OCAB和本文算法在宽带白噪声情况下,性能已经达到最优。这与式(7)的分析结果一致。图4和图5示出了在人造干扰(单频干扰和扫频干扰)下的四种算法的SINR对比。从图中可看出本文算法和MVDR算法SINR一致,优于其他两种算法,即本文算法性能已达最优。功率倒置算法能够有效抑制干扰,但是无法形成阵列增益,而OCAB算法在人造干扰情况下,性能严重恶化,这是由于人造干扰与卫星信号具备完全一致的周期平稳特性,基于式(5)和式(6)代价函数的OCAB算法会同时放大卫星信号及人造干扰。而本文算法考虑了卫星信号与干扰信号具备不同的循环频率这一特性,在人造干扰情况下,性能也达到了最优。

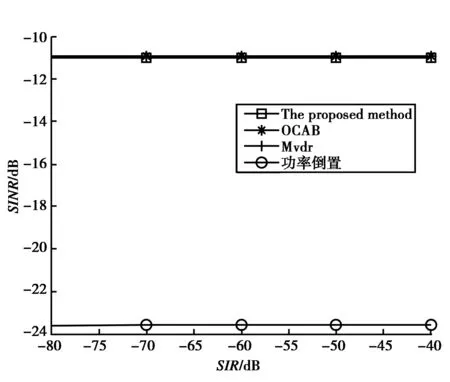
图3 宽带白噪声干扰下的输出信干噪比

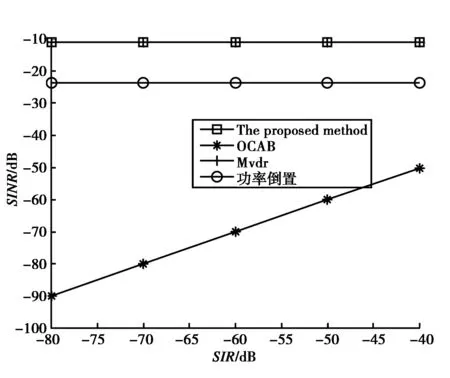
图4 单频干扰下的输出信干噪比

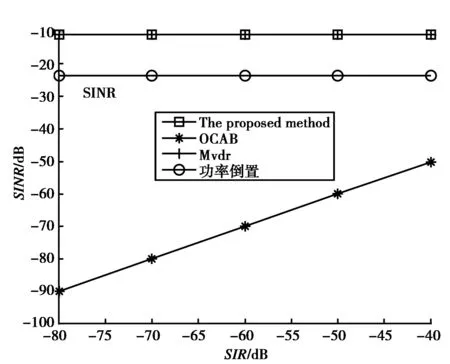
图5 扫频干扰下的输出信干噪比

5 结束语

基于北斗卫星信号的循环平稳特性,本文提出了一种新的北斗卫星抗干扰盲波束形成算法。该算法利用卫星信号与人造干扰之间不同的循环频率抑制干扰,无需DOA和参考信号先验信息,可以形成阵列增益,得到最优输出SINR,能够同时抑制宽带白噪声干扰和人造干扰。仿真结果验证了本文算法的有效性。本文中虽然使用的是北斗二代B3频点仿真环境,但可以推广到其他频点和卫星导航系统的抗干扰应用中,如GPS、GLONASS和Galileo.

[1] 张乃通,张中兆,李英涛. 卫星移动通信[M]. 北京:电子工业出版社,2000.

[2] MISRA P, BURKE B, PRATT M. GPS performance in navigation[J]. Proceedings of the IEEE. 1999, 87(1): 65-85.

[3] 王晓君,张伟,杜萌萌. 北斗卫星导航系统的应用及其抗干扰技术[J].河北工业科技, 2014,31(3):234-238.

[4] 徐海生.基于信道编码的卫星导航信号抗干扰技术研究[D].西安:西安电子科技大学,2009.

[5] 韩明. 基于混合扩频的卫星导航系统抗干扰技术研究[D]. 西安:西安电子科技大学,2009.

[6] CAPON J. High resolution frequency-wave number spectrum analysis[J]. Proceedings of the IEEE, 1969, 57(8): 1408-1418.

[7] KAY S M. Fundamentals of statistical signal processing: Estimation theory[M]. Englewood Cliffs, NJ: Prentice-Hall, 1993.

[8] COMPTON R T. The power-inversion adaptive array: concept and performance[J]. IEEE Transactions on Aerospace and Electronic Systems, 1979, 15(6):803-814.

[9] PARKINSON B W, SPILKER J J. Global positioning system: Theory and applications[M]. Boston: Artech House, 1996.

[10]SUN W, AMIN M G. A self-coherence anti-jamming GPS receiver[J]. IEEE Transaction on Signal Processing, 2005, 53(10): 3910-3915.

[11]GARDNER W A. Exploitation of spectral redundancy in cyclostationary signals[J].IEEE Signal Processing Magazine, 1991, 8(2): 14-36.

Beamforming Technique in Anti-Jamming Compass Receiver by Exploitation of Cyclostationarity

LI Lijun1,HUANG Jiyan2,LIU Zheng2

(1.ChinaRailwayConstructionEldctrificationBureauGroupCo.Ltd,Taiyuan030023,China; 2.UniversityofElectronicScienceandTechnologyofChina,Chengdu610054,China)

Although many anti-jamming methods in space domain have been proposed for satellite systems in the literature, they require the prior knowledge of DOA and reference signals, or cannot output optimal SINR since those algorithms suppressed both the desired signal and interference, or cannot mitigate the man-made interference. To counter the problems above, a novel blind beamforming method based on cyclostationarity of satellite signal is proposed in this paper for anti-jamming Compass Receiver. First, the cyclostationarities of compass signal and man-made interference are analyzed in the paper. An objective function based on the analysis results is constructed for the proposed method. Finally, the Lagrange method is used to obtain the solution. Compared with the existing methods, the proposed algorithm need not the prior knowledge of DOA and reference signals, can obtain the optimal array gains, and can suppress both the white noise interference and man-made intergerence. Theoretical analysis and simulation results are provided to show the effectiveness of the proposed method.

Compass Navigation Satellite System; man-made interference; cyclostationarity; signal to interference and noise ratio

10.13442/j.gnss.1008-9268.2017.03.009

2017-01-10

国家自然科学基金项目(批准号:61201275)； 中国铁建电气化局集团开放基金项目资助

P228.4

A

1008-9268(2017)03-0042-06

李利军 (1973-),男,高级工程师，现从事铁路四电工程、城市轨道交通机电设备安装工程的施工技术研究及施工管理。

黄际彦 (1981-),男,博士,副教授,主要研究方向为无线定位、阵列信号处理、通信中的信号处理技术等。

联系人: 黄际彦 E-mail: huangjiyan@uestc.edu.cn