非晶中结构遗传性及描述∗

武振伟李茂枝 徐莉梅 汪卫华

1)(北京大学物理学院,量子材料科学中心,北京 100871)

2)(中国人民大学物理系,北京 100872)

3)(中国科学院物理研究所,北京 100190)

非晶中结构遗传性及描述∗

武振伟1)†李茂枝2)徐莉梅1)汪卫华3)

1)(北京大学物理学院,量子材料科学中心,北京 100871)

2)(中国人民大学物理系,北京 100872)

3)(中国科学院物理研究所,北京 100190)

(2017年5月31日收到;2017年7月11日收到修改稿)

非晶态物质广泛存在于人们的日常生活和工业生产活动中,但人们对其原子结构及其结构与性能关系的认识还远不如对晶体材料那样充分.非晶态物质的原子结构不具备空间平移对称性,这使得传统针对晶体材料的实验技术和手段无法直接有效地应用到非晶态物质的结构分析中.用常规的衍射实验数据分析方法并不能直接地观察到非晶态物质的本征结构特征,但这些实验衍射数据往往隐含有极其重要的微观结构信息.本文简要综述了这些衍射数据背后所隐含的与金属玻璃中程序相关的结构信息.研究发现,非晶态物质中的一类隐含序与晶体结构中的球周期序紧密相关,意味着非晶态物质与晶体材料之间在原子结构上存在着非凡的同源性.进一步的研究结果还表明,不同隐含拓扑序之间纠缠的强弱与体系本身的玻璃形成能力存在明显的对应关系,这为衡量金属合金玻璃形成能力强弱的经验规律——混乱原理提供了微观结构上的理解,同时为进一步深入认识和理解非晶态材料衍射数据所隐含的微观结构信息提供了新的分析思路和方法.

非晶态物质,金属玻璃,结构遗传性

1 引 言

非晶态物质本征的原子排列方式一直是凝聚态物理和材料科学中最有趣和最基本的问题之一[1,2].与晶体材料不同,非晶态物质中原子的排列不具有长程有序性.但是,研究发现非晶态物质中存在着原子结构上的短程序甚至中程序.到目前为止,大量的科学研究都集中在对非晶态物质的短程序的描述和表征上[3−15],人们对其中程有序性的探讨和理解还处于刚刚起步的阶段[5−10].对非晶态物质中的中程序进行研究基于下面的这些问题:非晶态物质的微观是否遵循某些统一的规律?这些统一的规律是否与人们所熟知的晶体结构之间存在某些内在的联系?如果这些联系是真实存在的,那它将会以何种形式表现,并将怎样影响非晶态物质的物性?这些关键问题的回答,将有助于人们对非晶态物质原子结构本质的理解.事实上,非晶与其对应晶体之间的物性关系早已引起了人们的注意[15−22].早在20世纪50年代,就有科学实验报道晶体结构相对复杂的甘油或硅酸盐熔体可以被深度过冷[15],从而很容易得到其非晶态样品.但对于晶体结构相对简单的金属元素来讲,一般其对应熔体在实验室条件下只能被过冷几个开尔文,说明材料晶体结构的复杂程度与其玻璃形成能力之间具有一定的关联[17].此外,人们还认识到玻璃的结构中可能还包含部分晶体序,这些晶体序和局域五次对称性之间的几何阻挫通常被认为是液体过冷的结构基础[16−22].尽管已逐渐报道了大量的科研成果,人们对于玻璃和晶体之间的物性关联的物理起源仍不是十分清楚,这阻碍了人们对非晶态物质的原子结构及其结构-性能关系的进一步理解.

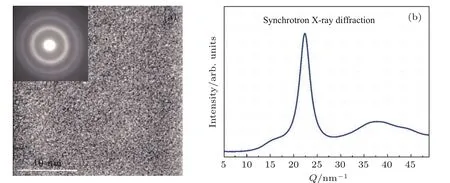
图1 非晶态物质的结构表征[10] (a)金属玻璃的高分辨透射电子显微镜照片,其中插图为选区电子衍射花样;(b)金属玻璃的同步X射线衍射数据曲线Fig.1.Structure characterization of metallic glasses[10]:(a)High-resolution transmission electron microscopy image and selected-area electron di ff raction pattern(inset);(b)the synchrotron X-ray di ff raction pattern.

实验室条件下,非晶态样品是通过快速降温液体避免结晶来获得.验证某种物质是否处于非晶态的实验手段有很多种,比如,X射线衍射、透射电镜或区域电子衍射技术[14].如图1所示,几乎所有的非晶态物质都具有类似的弥散环(区域电子衍射花斑)或扩展的衍射峰(X射线衍射)[10].但是,非晶态物质的原子结构在本质上却是千差万别的,它们在一定作用条件下的响应行为可能完全不同,具体表现为:保温处理以后所析出的晶体相不同[23−25];弹性极限和力学强度各异[26−31];阻抗晶化的热稳定性也存在差别[32−34].遗憾的是,造成这些不同的非晶态物质的本征结构上的差异,目前还不能通过简单的衍射实验数据分析而得来.诸如结构因子或对关联函数这类的实验衍射数据往往隐含有极其重要的微观结构信息.通过对大量金属玻璃的总体对关联函数的特征峰位的分析表明,金属玻璃中原子整体的堆垛方式包含了球周期序和局域平移对称性两种基本特征[9]如图2所示.与此同时,通过考察大量金属玻璃结构因子的第一峰峰位和相应的原子摩尔体积之间的关系[7],人们还发现金属玻璃的中程序具有类似分形的特征(图3).因此,对非晶态物质看似“杂乱无章”的衍射数据进行更加细致精确的描述和刻画十分必要,它有助于加深人们对非晶态物质本征结构特征的认识,并找到揭开不同玻璃结构本质差别的线索.

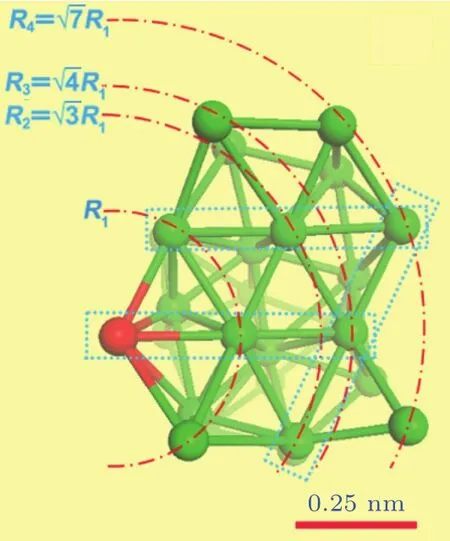
图2 金属玻璃中的球周期序和局域平移对称序[9]Fig.2.Spherical-periodic order and local translational symmetry in metallic glasses[9].

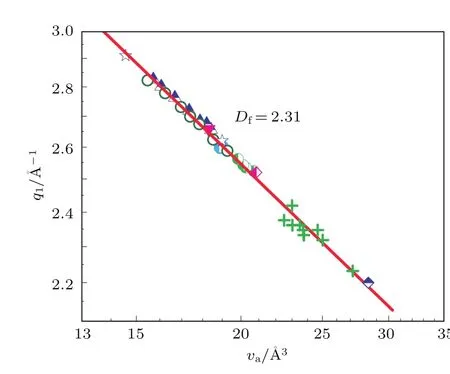
图3 金属玻璃中结构因子第一衍射峰(q1)与原子摩尔体积(va)之间的幂律关系,其中q1和va都在对数尺度下给出,图中红线为实验数据的拟合曲线,曲线斜率为2.31[7]Fig.3.Power-law scaling of the fi rst sharp di ff raction peak(q1)versus atomic volume(va)for a variety of metallic glasses.Both q1and vaare in a logarithmic scale.The solid line represents a linear fi t to the data[7].

本文重点介绍我们团队[35]对几种比较典型的金属玻璃的标度对关联函数(scaled pair correlation function,SPCF)进行的比较系统的分析.对于两种较为简单的单原子非晶Fe和Ni的研究表明,两种单原子金属玻璃在中程尺度上的原子堆积5方式有着本质上的区别:在非晶Fe当中隐含有部分体心立方结构所特有的原子排布方式(BCC有序排列),而在非晶Ni中却隐含了部分面心立方结构所特有的原子排布方式(FCC有序排列).这说明从球周期性的角度上,这两种不同的单原子非晶态物质的原子结构将与其相对应的晶体的晶格结构之间有着非凡的结构同源性.对三种二元非晶合金(包括CuZr,NiAl和NiCu)的标度偏对关联函数(scaled partial pair correlation function,SPPCF)进行分析发现每种体系中的隐含序列差异很大,相比单原子非晶情况要复杂很多,可能会同时混有BCC有序排列和FCC有序排列.这些不同的隐含序之间还有一定的概率发生结构上的相互纠缠,体系中的隐含序的种类和数量越多,它们之间发生纠缠的概率就越大,纠缠情况也会越复杂.进一步的分析表明,这种不同隐含拓扑序之间的纠缠的程度的大小与非晶合金的玻璃形成能力关系非常密切.本文还给出了一张金属玻璃中的隐含序列的图谱,从这张图谱中,人们可以更好地理解金属过冷熔体和金属玻璃的结构及其结构-性能关系.

2 金属玻璃中的隐含拓扑序

2.1 结构表征中的对关联函数

对关联函数(pair correlation function,PCF)是表征在相对中心原子距离为r的空间上发现其他原子的概率大小的一种关联形式,它可以在一定程度上反映体系中原子之间的平均距离和径向分布上原子结构的基本特征.不同元素a-b之间的偏对关联函数(partial pair correlation function,PPCF)的计算公式为

其中ρ为原子数密度;Na,Nb,和N分别是体系中两种不同类型的原子的数量和原子总数;rij为原子间距离.如果不对不同种类的原子加以区分,或者体系本身为单一元素系统,那么PCF的计算公式就可简单地表达成

对于非晶态物质而言,PCF上十几个Å范围以内的各个特征峰表征了其原子结构的短程到中程有序性,一些非常具体的原子结构信息隐含在这个范围内的峰位、半高宽和峰强之中.PCF上第一个峰值的产生由中心原子周围的最近邻所贡献,人们通常把它定义为短程序,超过第一峰位到大约1—2 nm距离上的各个峰位所表现出的原子结构特征,人们通常称之为中程序.随着r的增大,PCF逐渐趋于收敛,说明非晶中没有常规定义下的长程有序性.

2.2 单原子金属玻璃与其对应晶体之间的结构同源性

图4 温度为300 K时非晶态Ni和Fe的标度对关联函数曲线[35]FCC和BCC晶格结构标准序列中的特征常数以实竖线和虚竖线的形式在图中给出,可以明显地看到,Ni,Fe的各个标度峰的特征值与FCC或BCC标准序列里的某些特征常数具有明确的对应关系,因此,单原子非晶和其对应晶体之间在球周期序角度上具有类似的原子堆垛模式Fig.4.MD modeled PCFs of glassy Ni and Fe scaled by the fi rst peak position R1at 300 K[35]. The characteristic constants in corresponding FCC and BCC crystalline lattice structures(denoted by solid and dashed vertical lines,respectively)are also presented.It shows a clear correspondence of the scaled peak positions in PCFs of glassy Ni and Fe with some characteristic constants of FCC and BCC lattice structures.Thus,a pure glassy solid may share the same‘heart’or similar atomic packing nature with its crystalline counterpart.

图4 给出了非晶态Ni和Fe在温度为300 K时的SPCF,SPCF由对PCF进行重新标度得到,标度方式为PCF的自变量R被转换为R/R1,其中R1为PCF第一峰的峰位.可以明显地看出,在1.2 nm的长度范围内,曲线存在五个比较明显的特征峰,这些特征峰的出现预示着非晶态物质当中的一些短程到中程序的存在[35].通过对SPCF中各个标度峰的峰位Ri/R1(i=1,2,3,4,5)的集中分析发现,对于非晶态Ni,Ri/R1的数值分别为1.0,1.74,1.98,2.64和3.46,非常接近于一组常数数列仔细地分析考察非晶态Fe中Ri/R1的各个数值发现,它们分别为1.0,1.65,2.0,2.58和3.47.从以上数据分析可以看出,非晶态Ni和Fe的SPCF中,R1/R1,R3/R1和R5/R1三个标度峰的峰位数值几乎一致,但R2/R1和R4/R1两个峰的峰位数值却稍有不同.进一步研究发现,非晶态Fe中R2/R1和R4/R1的数值更加接近于常数但在非晶态Ni当中,这两个峰位的数值则更接近于常数.这种不同在接下来的分析研究中发现是意味深长和极其深刻的.表1给出了以上所讨论的数据.对比显示,不同种类的非晶态物质中Ri/R1数值对应于不同的特征常数,接下来的问题在于人们该如何来理解这些特征常数背后的物理意义,以及它们对体系的物性有何具体的影响.

表2给出了完美FCC和BCC晶格结构所对应的标准序列中的特征常数R0i/R01(i=1—14),这里的R0i表示第i层近邻原子相对于中心原子的距离.从表2中可以看出,R0i/R01(i=1—14)这组数值序列在FCC或BCC中是具有明显差异的,这种差异反映出FCC或BCC各自的本征晶格结构特征.从上述数据分析可以看出,一组特征常数序列可以用来表征其所对应的晶格结构,反之,不同的晶格结构就会表现出不同的特征常数序列.

表1 非晶态Ni和Fe的对关联函数中第一峰的峰位R1和被R1标度后的各个相对特征峰位,数据由分子动力学(MD)模拟得到[35]Table 1.The fi rst peak position R1and the relative atomic positions scaled by R1in the PCFs for glassy Ni and Fe obtained froMmolecular dynamics(MD)simulations[35].

表2 完美晶格点阵所对应的标准序列里的各个特征常数,表中共给出了四组数据,其中包括面心立方(F)、体心立方(B)、六角密排(H)和金刚石结构(D)Table 2.Relative atomic positions scaled by the fi rst peak position in four crystalline lattice structures.

对表1和表2中的数据进行对比分析可以得出以下规律:非晶Ni的SPCF中各个峰位特征值Ri/R1(i=2,3,4,5)对应于FCC晶格结构中的某些特征常数但对于非晶Fe而言,这组特征值序列更加接近于BCC晶格结构当中的一组特征常数序列从上述数据对比和图4所示的内容可以看出,单原子金属玻璃中的原子排布方式与其对应晶体的晶格结构之间有着某种潜在的联系,文献[35]把这种潜在的联系定义为两者在原子结构层面上的同源性(structure homology).在快速冷却液体而得到非晶态物质的过程中,一些晶体结构中所特有的原子排布规律被以某种特殊的方式“表达”到了非晶态物质当中,这些特征性的原子排布方式一般会隐含在实验衍射数据背后,且不容易被显而易见地观察到,可以称之为非晶态物质中的隐含拓扑序(hidden topological orders).

2.3 多组分金属玻璃中的隐含拓扑序

单原子金属玻璃与其对应晶体在原子结构上所表现出的非凡的同源性促使人们进一步对多元金属玻璃的隐含序进行了考察.文献[35]分析计算了四种多元金属玻璃Cu50Zr50,Ni50Al50,Ni50Cu50和Cu46Zr46Al8的各个组分之间的PPCF,并对PPCF做了相应的标度处理(SPPCF),所得的各个峰位特征值由表3给出.简单分析可以看出,多元非晶合金中隐含序分布情况比之前所述的单原子体系要更加复杂有趣.以非晶Cu50Zr50为例,Cu-Zr之间的PPCF中的所有特征值Ri/R1(i=2,3,4,5)都可以单一地从FCC标准序列中找到对应的特征常数.而在Cu-Cu之间的PPCF中,情况有所不同,其中Ri/R1(i=2,3,4)的取值可从FCC标准序列中找到对应,但R5/R1的取值(约3.6√7)更加接近于BCC标准序列中的一个特征常数类似的特点在Zr-Zr之间的PPCF中也有出现,其中Ri/R1(i=2,3,5)的取值可全部从BCC标准序列中找到对应,但R4/R1的取值(约2.41)却是来自于FCC标准序列.因此,Cu-Cu或Zr-Zr的PPCF中的隐含序,并不能由单一的FCC或BCC标准序列中的特征常数构成,这两组隐含序列中出现了来自不同晶格结构的特征常数的“杂化”.这种“杂化”现象是具有物理意义的,随后的论述将对这一现象和问题展开讨论.以上数据说明,在非晶态Cu50Zr50中存在三种不同的隐含序,且其中有两种隐含序存在“杂化”现象.

在非晶态Ni50Al50中,Ni-Ni和Ni-Al的隐含序中的特征值Ri/R1(i=2,3,4,5)可全部单一地从FCC标准序列中找到对应,而且它们所对应的特征常数也都完全一致,这表明Ni-Ni和Ni-Al的PPCF中隐含序是相同的.Al-Al中的隐含序则与上面提到的两组数据不同,它是一个“杂化”序列,其中Ri/R1(i=2,3,4)的取值都可以在BCC标准序列中找到对应,而R5/R1的取值(约3.11)则更倾向于来自FCC标准序列里的特征常数因此,在非晶Ni50Al50中,存在两种不同的隐含序,并且有一种是“杂化”的.对于非晶态Ni50Cu50而言,情况比较简单,它的所有PPCF中的隐含序的特征值都可单一地从FCC标准序列中找到对应,且对应的特征常数完全一致,说明在非晶态Ni50Al50中只存在一种隐含序,非常类似于单原子金属玻璃中的情形.最后对非晶态Cu46Zr46Al8做相应的考察发现,少量Al元素的引入使得体系中的隐含序变得更加复杂,如表3所列.Zr-Cu,Cu-Cu和Cu-Al的PPCF中的隐含序的特征值都可单一地来源于FCC标准序列,但它们所对应的特征常数有所不同,构成三种不同的隐含序.Zr-Al之间的PPCF对应一种来自于BCC标准序列的隐含序.Zr-Zr之间的隐含序具有如上所述的“杂化”现象,其中

Ri/R1(i=2,3,5)的取值可认为来自于BCC标准序列,而中R4/R1的取值(约2.43)更加接近于是来自于FCC标准序列里的特征常数.

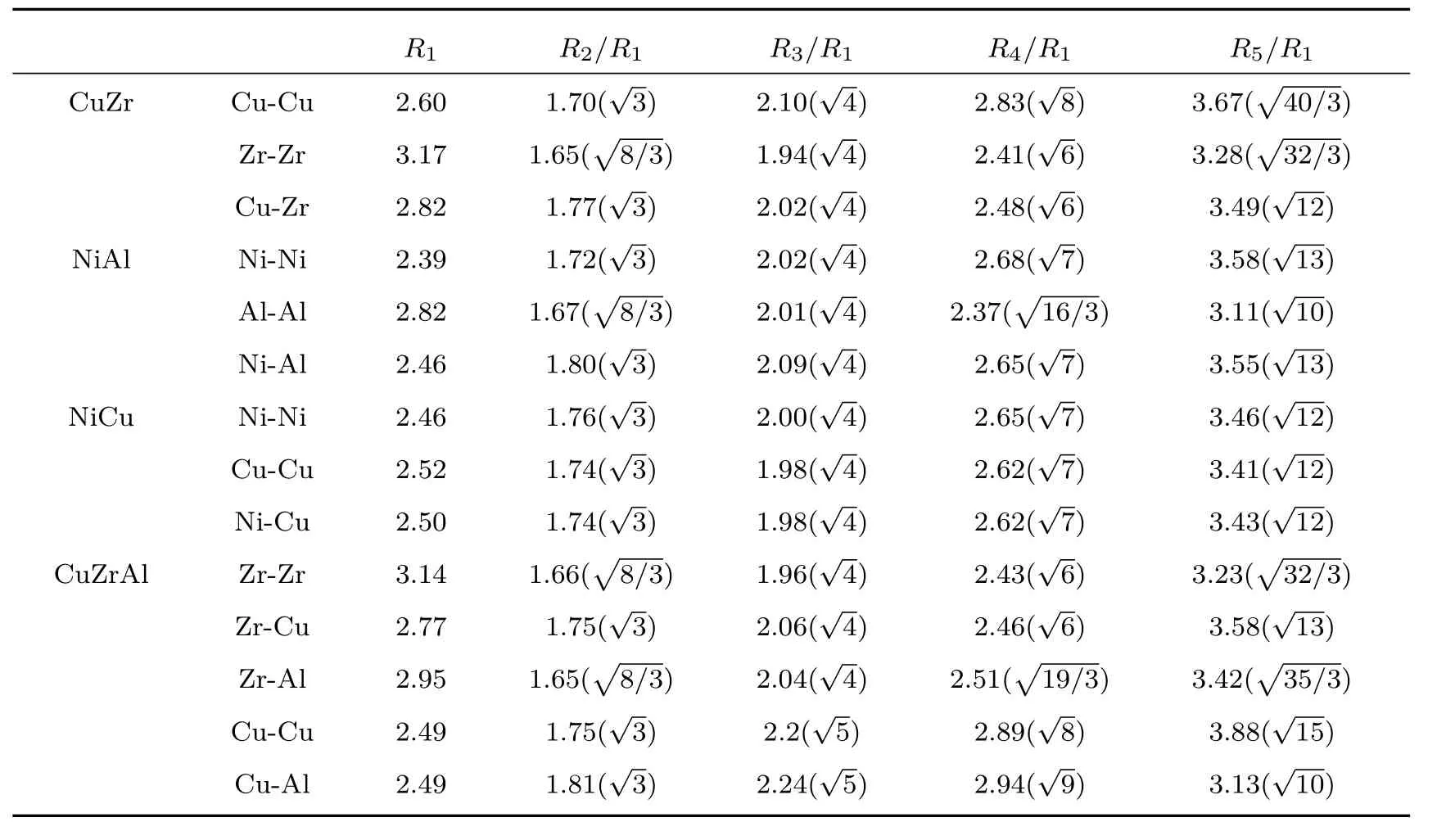
表3 非晶态CuZr,NiAl,NiCu和CuZrAl中各组偏对关联函数的第一峰峰位和各个对应标度峰的特征值[35]Table 3.The fi rst peak position R1and the scaled peak positions by R1in partial PCFs of CuZr,NiAl,NiCu,and CuZrAl metallic glasses obtained froMMD simulations[35].

2.4 金属玻璃中的隐含序图谱

基于以上的数据处理和分析可以得知,在金属玻璃的形成过程中,某些特定的原子排布方式(隐含序)会逐步建立起来,并隐藏于体系的PPCF或各种实验衍射数据中,这些隐含序中所出现的特征值并不是平凡和无规律可循的,它们往往对应于FCC或BCC标准序列里的某些特征常数.

如果将FCC或BCC标准序列中的特征常数看作是某种原子排列方式的基本结构“基因”,那么FCC或BCC的标准结构序列便可被认定为是一种标准“基因”谱.在玻璃形成过程中,体系继承和表达了来自于标准“基因”谱的某些特定的结构“基因”,这些结构“基因”的排列组合决定着这个体系中所特有的原子排布方式,这种原子排布规律的一种表示方法就是隐含序,它可以通过对体系的实验衍射数据进行分析得到.基于以上的类比假设,武振伟及其合作者[35]构建了一张能够更好地表达非晶中的隐含序与标准“基因”谱对应关系的非晶态物质结构“基因”图谱.如图5所示,FCC和BCC晶格结构所对应的标准“基因”谱分别以短红线和短蓝线来表示构成,其中每条短线代表FCC或BCC标准序列里的一个结构“基因”,它们之间的相对位置由其对应的标准序列里的特征常数来决定.对于某种金属玻璃,其PPCF中的峰位特征值被当成是一种遗传自标准序列的结构“基因”,用彩色柱状标记于相应位置,颜色与标准“基因”相对应.从图5可以看出,单原子金属玻璃从标准“基因”谱中继承了最少种类的结构“基因”,随着体系中化学元素组分的增加,越来越多不同种类的结构“基因”被遗传到金属玻璃的原子结构当中去.例如,在Cu50Zr50体系中掺杂少量的Al元素便会导致两种新的隐含序和七种新的结构“基因”在Cu46Zr46Al8体系中出现.很显然,不同的金属玻璃具有种类不同的隐含序,但在组成这些隐含序的结构“基因”中,某些结构“基因”的出现频次很高,例如总会出现的原因是显而易见的,总会出现对应着体系具有一定的局域平移对称性.也相当普遍,对应一些近等边三角形共边连接式的局域原子构型[36].另外,某些结构“基因”好像从来不会被遗传到金属玻璃当中去,它们对应FCC标准谱中的,以及BCC标准谱中的

最后需要强调的是,标准“基因”谱并没有引入完美HCP(c/a=)结构的特征常数,一是因为完美HCP中的特征常数绝大部分已被包含在FCC和BCC标准序列当中,二是特定的HCP结构其特征常数依赖于比值c/a,所以它并不具备FCC或BCC结构那样好的一般性.表2也给出了金刚石结构中的特征常数,数据显示,这些特征常数都已包含在FCC和BCC标准谱当中.综上所述,FCC和BCC结构所对应的特征常数更加具有一般性来代表结构“基因”,因此适宜用来作为结构的标准“基因”谱.

图5 金属玻璃的结构“基因”遗传图谱,从图中可以清晰地看出各个体系的玻璃形成能力与体系中隐含序的种类多少的关系Fig.5. The “genetic map” of hidden orders in metallic glasses.More “gene”sequences are often inherited in metallic glasses,as the number of component increases,so that more di ff erent hidden orders are formed.The hidden orders in a metallic glass are closely correlated with the glassforming ability of the metallic alloy.

3 隐含序与玻璃形成能力

2.4 节数据表明,单原子金属玻璃仅从标准“基因”谱中继承种类较少的结构“基因”,进而形成隐藏在体系原子结构背后的单一隐含序.对于二元非晶而言,标准谱中更多的结构“基因”被遗传到了体系当中,它们不同的组合形式使人们看到了种类繁多的隐含序.图6给出了非晶Cu50Zr50,Ni50Al50和Ni50Cu50的SPPCF曲线.在Cu50Zr50中三组SPPCF形态各异(图6(a)),表明体系中Cu-Cu,Cu-Zr和Zr-Zr之间所对应的原子排布方式有着明显不同.图6(a)非常形象地表现出Cu50Zr50中三种不同的隐含拓扑序之间的纠缠,暗示出体系中原子排列方式上的错综复杂.而在Ni50Cu50中(图6(c)),情况非常简单,三组SP-PCF曲线重合在了一起,表明体系中并没有由于不同的隐含拓扑序而导致的原子排布上的纠缠.Ni50Al50中的状况介于Cu50Zr50和Ni50Cu50之间.由于Ni-Ni和Ni-Al的PPCF中遗传有相同的隐含序,因此它们的SPPCF曲线形式上非常类似,从图6(b)可以看出,它们都与Al-Al之间的SPPCF曲线有一定程度上的“纠缠”,这是因为Al-Al之间隐含序区别于另外两组PPCF中的隐含序.以上结果表明,如果非晶态物质中存在两种或两种以上不相同的隐含序,那么这些不同的隐含序所对应的原子结构就会出现排列组合方式上的纠缠,体系中的隐含序种类越多,其中的纠缠就可能越强烈.此外,可以看到金属玻璃中大多数的隐含序所对应的组成结构“基因”都可以单一地从FCC(或BCC)的标准谱中找到,但对于某些特殊的隐含序,例如Cu50Zr50中的Cu-Cu和Zr-Zr之间,所谓“杂化”隐含序的现象时常发生,意味着这些隐含序中的结构“基因”并不能单一地从FCC(或BCC)的标准谱中找到,而是混合了来自FCC和BCC标准谱中的某些特定的结构“基因”.这些具有“杂化”性质的隐含序,会使得多组分非晶合金体系中隐含拓扑序的纠缠变得更加复杂.

图6 三组二元金属玻璃的标度偏对关联函数[35] (a)Cu50Zr50的各条标度偏对关联函数曲线相互缠绕在一起,说明体系内部的隐含序在结构上是相互纠缠的;(b)Ni50Al50中的状况介于(a)和(c)两者之间;(c)Ni50Cu50的所有标度偏对关联函数曲线重合,体系内部隐含序只有一种,所有该体系中不存在所谓拓扑结构上的纠缠Fig.6.The partial PCFs scaled by the fi rst peak position in three binary metallic glasses[35]:(a)In Cu50Zr50metallic glasses the partial PCFs entangle with each other,implying that these hidden orders are entangled topologically;(b)the situation of Ni50Al50metallic glass falls in between Cu50Zr50and Ni50Cu50;(c)in Ni50Cu50metallic glass,however,the scaled partial PCFs are almost collapsed together,indicating a very single hidden order,so that there is no order entanglement in this system.

4 隐含序与非晶物性的讨论

非晶态物质与晶体材料之间的结构同源性,以及非晶态物质中的隐含拓扑序的纠缠,对于理解玻璃及其玻璃转变方面的某些关键问题,可能起着至关重要的作用.隐含序与非晶态物质中原子结构的中程序密切相关.玻璃与晶体之间的结构同源性提示人们或许可以尝试从晶体的角度来探讨非晶中的一系列重要问题,例如最近的一项研究结果表明,金属玻璃与其对应晶体材料在力学性质方面关系密切[37],某种程度上也反映出非晶与晶体之间在原子结构层面上的某些相似性.

另一方面,非晶中隐含拓扑序的纠缠可能与体系的玻璃形成能力(glass forming ability,GFA)密切相关.体系中含有不同种类的隐含序在一定程度上反映了非晶合金中原子排布结构上的几何阻措.这种隐含序背后复杂的纠缠所导致的中程原子堆垛方式上的高度几何阻挫,提高了过冷液体阻抗晶化的能力,从而最终导致了某些金属合金体系具有良好的玻璃形成能力.这里用CuZr和NiAl合金来举例说明,这两者的玻璃形成能力差异很大,等效晶化速率非常不同[32],但两者在液体结构上并不存在某些平均性质上的明显差异[32],这使得从常规角度理解二者GFA的异同变得非常困难.然而,如果从隐含拓扑序的纠缠这个简单的物理图像出发,二者在玻璃形成能力上的差异可以很自然地得到解释:在玻璃形成过程中,CuZr体系比NiAl合金形成了更多的原子排布上的隐含序,这些隐含拓扑序的纠缠所导致的原子中程结构上的几何阻挫,最终导致CuZr合金的GFA要优于NiAl合金.同样的物理图像可以用来解释为什么NiCu合金的GFA如此之差,如表3所列,非晶NiCu中只存在一种隐含序,系统内部也就不会存在隐含拓扑序纠缠所导致的中程原子结构上的几何阻挫,从而最终导致了NiCu合金较差的GFA.这一点可以从MD模拟中非常直观地观察到,因为NiCu合金要使用相对于CuZr或NiAl高得多的降温速率才能得到其非晶态构型.实验上,微量掺杂是提高某种金属合金GFA的非常有效的手段[38,39],例如在CuZr中掺入少量的Al元素可以非常显著地提升体系的GFA,实验室制备非晶样品的临界尺寸可以从Cu50Zr50时的1 mm提升到Cu46Zr46Al8时到8 mm,掺杂效果非常明显[38,40].如果从隐含拓扑序纠缠的角度来对上述现象加以解释,那么微量掺入Al元素后,更多的隐含序被引入到体系当中(表3),隐含序之间复杂的纠缠所导致的高度几何阻挫有效地提升了体系的玻璃形成能力.

迄今为止,为找到具有更好GFA的金属合金体系,实验上总结出了一系列的经验规律,比如具有好的GFA的体系中通常至少含有三种原子尺寸不同的化学元素.这些经验规律或者混乱原理[41]都可以认为是不同隐含拓扑序之间的纠缠的外在表现,其中隐含序纠缠是它们的原子结构的起源.如在上面的讨论中提到的那样,化学组分的增加一般情况下都会导致系统引入更多的隐含序,从而更容易产生几何阻挫而抑制系统的晶化.同样,系统中各个化学组分之间原子尺寸大小差异较大时,也会相对更加容易地使体系引入更多的隐含序,从而增强系统的GFA.因此隐含拓扑序之间的纠缠是实验上获得具有良好GFA的合金体系的经验规律或混乱原理的结构根源,这一新的物理图像将为人们寻找具有优异GFA的合金体系提供新的途径.

5 结 论

与晶体材料不同,非晶态物质的原子排布不具有长程有序性.虽然已有众多的科学研究揭示出非晶中存在原子结构上的短程序甚至中程序,但到目前为止非晶态物质中原子排布的本质规律仍然是一个谜,同时也是凝聚态物理和材料科学领域最基本、最深刻、最有趣的问题之一.对于晶体材料而言,其原子结构可以采用现代微观结构分析技术如X射线衍射加以表征和研究.然而,这些表征和分析手段对于非晶态物质的结构探究而言却并不是那么的有力,不同非晶合金的衍射实验数据表面看上去非常类似,以至于区分不同非晶态物质的微观结构的差异变得非常困难,但它们的诸多物理性能如强度和韧性有着本质的区别,它们的热稳定性和GFA也存在很大不同,这些实验事实都从不同的角度说明了非晶态物质的微观原子结构是千差万别的,是有待进一步深刻分析和研究的.因此,非晶态物质的实验衍射数据背后是否隐含着其微观原子排布的某些规律,就是一个十分关键和有待进一步研究的问题,这也是本文的基本出发点之一.

武振伟等[35]采用MD模拟方法,通过对几种具有代表性的金属玻璃结构的衍射特征峰进行了更加详尽细致地分析后发现,在这些衍射特征峰的背后隐含着金属玻璃中程序的结构信息,并由此发展了一种新的表征非晶态物质结构中程序的方法.对于单原子非晶而言,隐含的中程序与相应晶体结构的球周期序紧密相关,表明在玻璃形成过程中,单原子非晶继承了部分的晶体球周期序,这也意味着非晶态物质与晶体材料之间存在着非凡的结构同源性.随着金属玻璃体系中化学组分的增加,这些中程尺度上的隐含序的种类也会随之增加.进一步的研究结果还表明,不同隐含拓扑序之间纠缠的强弱与体系本身的玻璃形成能力之间存在明显的对应关系,这个发现为金属熔体冷却过程中结构阻挫的形成从而抑制金属熔体的晶化而最终导致非晶态物质的形成提供了一个新的微观结构演化的物理图像,也为实验上寻找玻璃形成能力强的金属合金体系提供了新的理论思路.非晶态物质中隐含序的研究为衡量金属合金玻璃形成能力强弱的经验规律——混乱原理提供了微观结构上的理解,同时为进一步深入认识和理解非晶态材料衍射数据所隐含的微观结构信息提供了新的分析思路和方法.

[1]Anderson P W 1995 Science 267 1611

[2]Yavari A R 2006 Nature 439 405

[3]Bernal J D 1960 Nature 185 68

[4]Gaskell P H 1978 Nature 276 484

[5]Miracle D B 2004 Nat.Mater.3 697

[6]Sheng H W,Luo W K,Alamgir F M,Bai J M,Ma E 2006 Nature 439 419

[7]Ma D,Stoica A D,Wang X L 2009 Nat.Mater.8 30

[8]Li M,Wang C Z,Hao S G,Kramer MJ,Ho K M2009 Phys.Rev.B 80 184201

[9]Liu X J,Xu Y,Hui X,Lu Z P,Li F,Chen G L,Lu J,Liu C T 2010 Phys.Rev.Lett.105 155501

[10]Zeng Q,Sheng H,Ding Y,Wang L,Yang W,Jiang J Z,Mao W L,Mao H K 2011 Science 332 1404

[11]Hirata A,Kang L J,Fujita T,Klumov B,Matsue K,Kotani M,Yavari A R,Chen MW 2013 Science 341 376

[12]Pan S P,Qin J Y,Wang W M,Gu T K 2011 Phys.Rev.B 84 092201

[13]Zallen R 1983 The Physics of Amorphous Solids(Wiley Online Library)

[14]Luborsky F 1983 Amorphous Metallic Alloys(London,UK:Butterworth and Co(Publishers))

[15]Frank F C 1952 Proc.R.Soc.London Ser.A 215 43

[16]Nelson D R 1983 Phys.Rev.B 28 5515

[17]Watson R E,Bennett L H 1983 Scripta Metall.17 827

[18]Steinhardt P J,Nelson D R,Ronchetti M1981 Phys.Rev.Lett.47 1297

[19]Cheng Y Q,Ma E 2011 Prog.Mater.Sci.56 379

[20]Leocmach M,Tanaka H 2012 Nat.Commun.3 974

[21]Tanaka H,Kawasaki T,Shintani H,Watanabe K 2010 Nat.Mater.9 324

[22]Tanaka H 2005 J.Non-Cryst.Solids 351 3385

[23]Greer A L,Cheng Y Q,Ma E 2013 Mater.Sci.Eng.R 74 71

[24]Schneider S,Thiyagarajan P,Johnson W L 1996 Appl.Phys.Lett.68 493

[25]Mattern N,Kühn U,Hermann H,Ehrenberg H,Neuefeind J,Eckert J 2002 Acta Mater.50 305

[26]Schroers J,Johnson W L 2004 Phys.Rev.Lett.93 255506

[27]Dimiduk D M,Woodward C,LeSar R,Uchic MD 2006 Science 312 1188

[28]Chen M,Inoue A,Zhang W,Sakurai T 2006 Phys.Rev.Lett.96 245502

[29]Liu Y H,Wang G,Wang R J,Zhao D Q,Pan MX,Wang W H 2007 Science 315 1385

[30]Wang W H 2012 Nat.Mater.11 275

[31]Greer A L 1995 Science 267 1947

[32]Tang C,Harrowell P 2013 Nat.Mater.12 507

[33]Suryanarayana C,Seki I,Inoue A 2009 J.Non-Cryst.Solids 355 355

[34]Lee S W,Huh MY,Fleury E,Lee J C 2006 Acta Mater.54 349

[35]Wu Z W,Li MZ,Wang W H,Liu K X 2015 Nat.Commun.6 6035

[36]Bennett C H 1972 J.Appl.Phys.43 2727

[37]Makarov A S,Khonik V A,Mitrofanov Y P,Granato A V,Joncich D M,Khonik S V 2013 Appl.Phys.Lett.102 091908

[38]Wang W H 2007 Prog.Mater.Sci.52 540

[39]Lu Z P,Liu C T 2004 J.Mater.Sci.39 3965

[40]Yu H B,Wang W H,Bai H Y 2010 Appl.Phys.Lett.96 081902

[41]Greer A L 1993 Nature 366 303

PACS:64.70.pe,81.05.Kf,61.43.BnDOI:10.7498/aps.66.176405

*Project supported by the National Basic Research PrograMof China(Grant No.2015CB856801),the National Natural Science Foundation of China(Grant Nos.11525520,51631003),and the China Postdoctoral Science Foundation(Grant No.2017M610687).

†Corresponding author.E-mail:zwwu@pku.edu.cn

Inherited structure of amorphous matter∗

Wu Zhen-Wei1)†Li Mao-Zhi2)Xu Li-Mei1)Wang Wei-Hua3)
1)(International Center for QuantuMMaterials,School of Physics,Peking University,Beijing 100871,China)
2)(Department of Physics,Renmin University of China,Beijing 100872,China)
3)(Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China)

31 May 2017;revised manuscript

11 July 2017)

The inherent atomic packing mode of glassy solid is still one of the most interesting and fundamental problems in condensed-matter physics and material science.Although signi fi cant progress has been made and provided insights into the atomic-level structure and short-to-medium-range order in glass,the way of leading to the medium-range order is still unclear.Does a universal rule exist in nature to construct a glass structure as what has been discovered for crystals?Is there any connection between glassy and crystalline structures?If so,what does the connection look like and how is the connection related to the properties of the glassy solids?A glassy state is usually obtained through supercooling a liquid fast enough to avoid crystallization.The amorphous nature of glassy solid is experimentally ascertained by X-ray di ff raction(XRD),transmission electron microscopy or selected area electron di ff raction(SAED).Almost all kinds of glassy solids exhibit similar maze-like SAED patterns without any local lattice fringes and broad di ff raction maximuMcharacteristics in XRD data.However,the glassy solids are inherently di ff erent in atomic-level structure,demonstrated by their di ff erent response behaviors under certain conditions,for example,the diverse annealing-precipitated crystallinephases,the distinct mechanical strengths and ductilities,and the di ff erent thermal stabilities against crystallization.Unfortunately,such a di ff erence in inherent structure among glassy solids cannot be easily di ff erentiated froMa trivial analysis of the experimental di ff raction data.However,the di ff raction data such as structure factors or pair correlation functions(PCFs)are not as trivial as they look like.On the contrary,some studies have demonstrated that plenty of structural information is hidden behind the data of structure factors or PCFs,for example,global packing containing both spherical-periodic order and local translational symmetry has been revealed by analyzing PCFs of many metallic glasses.A fractal nature of medium-range order in metallic glassis also found by examining the relationships between the fi rst peak positions in structure factors and atomic molar volumes in many metallic glasses.In fact,the oscillation in the structure factor or PCF is an indication that a certain order does exist in amorphous solid.Therefore,a more careful scrutiny of the di ff raction data is desired to gain a more in-depth insight into the glassy structure features and fi nd a clue to unveil the natures of the inherent structures in di ff erent glasses.In this paper,we brie fl y review the recent molecular dynamics simulation results that the distinct hidden orders of atomic packing formula in mediuMrange in these pure glassy solids are unveiled to be inherited froMbcc order in glassy Fe and fcc order in glassy Ni,respectively,re fl ecting nontrivial structural homology between glassy and crystalline solids.By analyzing the partial PCFs of three two-component metallic glasses of CuZr,NiAl,and NiCu which are similar but have distinct glass-forming ability viaMD simulations,very di ff erent hidden orders are observed in each individual system,indicating that the hidden orders are more complex in multicomponent metallic glasses.The di ff erent hidden orders in a multicomponent metallic glass may be entangled topologically.More di ff erent hidden orders lead to more complex topological entanglement.Further analysis indicates that the formation of the hidden orders during cooling and their topological entanglement produces the geometrical frustration against crystallization and is closely correlated with the glass-forming ability of metallic alloys.A “genetic map”of hidden orders in metallic glass is fi nally constructed,which provides new insights into the structural properties and structure-property relationships in metallic glass-forming liquids and glasses.

amorphous solid,metallic glass,inherited structure

10.7498/aps.66.176405

∗国家重点基础研究发展计划(批准号:2015CB856801)、国家自然科学基金(批准号:11525520,51631003)和中国博士后科学基金(批准号:2017M610687)资助的课题.

†通信作者.E-mail:zwwu@pku.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn