胶体在非晶研究中的应用∗

陈科

(中国科学院物理研究所,北京 100190)

胶体在非晶研究中的应用∗

陈科†

(中国科学院物理研究所,北京 100190)

(2017年7月3日收到;2017年8月8日收到修改稿)

胶体玻璃作为一种软物质材料由于其独特的物理化学特性在非晶态物理的研究中有重要的应用.本文简要介绍了胶体玻璃与玻璃材料的联系,并通过具体的研究实例介绍了胶体玻璃在研究非晶结构、动力学以及热力学方面的应用,对胶体玻璃未来的研究进行了展望.

胶体,玻璃,非晶态材料

1 引 言

1.1 非晶中的基本物理问题

玻璃,又称非晶固体(amorphous solid),是一大类固体材料,包括常见的以二氧化硅玻璃为代表的氧化物玻璃,以塑料为代表的高分子玻璃,以及金属玻璃等.非晶材料除了在日常生产生活中有大量应用外,还在工业、能源、信息和国防等高技术领域有重要的应用价值和前景.例如,软磁非晶合金制作的变压器能够降低24%—48%的交流电传输损耗,非晶的自锐和耐磨的特性可应用于穿甲弹和舰艇甲板涂层上,非晶材料制作的核废料容器能够长时间防止放射性材料的泄漏.同时,非晶材料的应用也存在一些突出的问题,包括非晶材料的脆性,非晶材料的老化,以及非晶产品的均一性等.如何设计和调控非晶材料的性能是非晶材料发展和应用的瓶颈问题.目前,非晶生产工艺主要还是依赖试错的经验指导.这是由于目前对非晶体系中的基本物理问题缺乏清晰深入的了解和广泛有效的理论框架.

非晶中的基本物理问题大致可以分为三类,包括非晶的微观结构、动力学以及热力学问题,其中最根本的问题是非晶的微观结构.科学上对于一个材料的认识总是从结构和相互作用两个角度出发,建立基本的物理学模型,推导出材料的宏观性质.对于大部分晶体材料,原子的排布比较简单,可以用一个代表性的原胞来描述大量原子组成的晶格,材料性质的复杂性主要体现在原子间的相互作用上,例如半导体或超导体材料.然而对于大部分非晶材料,原子间的相互作用是相对简单的金属键或共价键,而材料结构则没有任何可测量的特征,也没有发现明显的组成非晶材料的基本结构单元.因此,结构的不定型性是非晶材料复杂性的来源.非晶材料结构形成于非晶制备过程,非晶固体通过迅速冷却液体得到,在液体迅速冷却的过程中,原子来不及形成有序的晶体结构就被“冻结”住了,因此非晶的结构缺乏周期性.现代材料结构表征技术,如X射线衍射和中子散射技术,主要探测的是原子排列的空间周期性,当应用在非晶材料中时只能得到大量平均之后的结果,无法在原子尺度上揭示非晶中原子排列的细节.如果说晶体的周期性结构为建立晶体材料的物理模型提供了一个起点,那么非晶结构信息的缺失使得建立非晶基本物理模型变得十分困难,尤其考虑到大量粒子带来的结构复杂性约随着粒子数的阶乘(N!)增加.如何从实验上更准确的测量和分析非晶结构特征是当前非晶研究的一个前沿问题.

图1 不同材料的玻璃化转变曲线[1]Fig.1.Viscosity for di ff erent glass-forming liquids during glass transition[1].

非晶中最令人惊讶的实验现象为“玻璃化转变(glass transition)”现象.当液体的温度下降到玻璃化转变温度Tg附近时,液体的黏度在很小的温度范围内会发生超过十个数量级的变化,如图1所示.原子运动的弛豫时间也从ps(1 ps=10−12s)量级增加到100 s量级.虽然通常原子的运动会随着温度的下降而减慢,然而在玻璃化转变过程中温度的下降幅度(十几K左右)远远不能解释其动力学变慢的程度.什么原因使玻璃在这么小的温度范围内,动力学从自由扩散的液体到几乎只有振动自由度的固体,这就是困扰了物理学近一个世纪的玻璃化转变难题.玻璃化转变过程中的另一个问题是玻璃中的弛豫时间是否发散,这决定了应该把玻璃材料划为是固体还是极端黏稠的液体.根据经验,玻璃是固体毋庸置疑.常见的玻璃材料显然满足人们对于固体的一般感性认识,例如非常坚硬、在冲击下会碎裂等.然而,黏度非常高的流体也能在短时间尺度上表现出类似固体的性质,在很长的时间尺度上表现出流动性.例如澳大利亚昆士兰大学的一个研究项目数十年来观察一块漏斗中凝固的沥青.这块沥青看上去完全是一个坚硬的固体,然而每8年左右这块沥青就会滴下来一滴,我们通常所见的玻璃材料的黏度比这块沥青还要高得多[2].除了玻璃化转变这一难题以外,玻璃中还有很多其他的动力学问题,例如,玻璃材料中存在着特征时间范围非常广的各种弛豫过程,同时玻璃中的局域动力学在空间上和时间上都存在不均匀性,这些动力学现象的微观起源也是目前正在探索的问题.

从统计物理的角度看,玻璃不是一个热力学的平衡态,而是处在亚稳态(metastable),玻璃内部时刻都在发生弛豫过程,对这样的系统原则上很难建立严格的热力学模型.然而,由于玻璃中的弛豫过程十分缓慢,实验上可以近似的把玻璃态作为一个平衡的热力学状态来研究,通过测量玻璃材料的比热和声子振动模式了解玻璃内部能量的分布和变化.实验研究发现,玻璃材料的比热在低温区存在一个“异常”高的比热峰,相应的声子振动模式在低频段也存在高过晶体材料的声子态密度(图2),这两个实验现象(比热峰和振动态密度峰)一般都被称为玻色峰(Boson peak)[3,4].比热和振动态密度的实验现象是相互关联的,这表明在玻璃材料中存在大量的低频振动模式,这些低频振动模式在比热上表现为在低温区间能够“容纳”更多的热量.值得注意的是,玻色峰在玻璃材料中广泛存在,并且和材料的力学性能有非常密切的关系,这说明尽管不同的非晶体系在组成和结构上千差万别,它们在内部集体运动方面有很多共同的特征,发现和理解这些特征对于理解非晶的本质有重要的意义.同样,由于实验手段的局限,目前对于玻色峰的微观起源仍然没有公认的物理机制.

图2 氧化硼玻璃的低温比热[5]Fig.2.Low temperature speci fi c heat of B2O3[5].

从非晶中的基本问题可以看出非晶研究中的一个根本困难在于:由于缺乏有效的微观实验观测手段,对非晶的微观结构和运动的了解十分有限.尽管能够通过动力学和热力学的测量了解非晶内部的运动规律,这些结果对于掌握完整的非晶微观信息来说无异于管中窥豹.这一困难严重制约了非晶理论框架的建立,使得很多基本的物理问题无法得到确定的判断.探索新的观测非晶微观结构和运动的实验系统和方法成为非晶物理研究的一种重要方向.胶体玻璃作为一个模型系统为非晶物理的微观细节的研究提供了一个有效的平台.

1.2 胶体和胶体玻璃

胶体(colloids)一般是指固体颗粒和连续介质的混合物,其中固体颗粒的尺寸在10 nm—10µm之间.最常见的胶体体系是固体粒子分散在液体中,例如日常生活中的牛奶、墨水、油漆等都是这一类的胶体溶液.由于胶体粒子的尺寸较小,溶液中的胶体粒子有非常显著的热运动,这一点和原子及分子的运动十分相似.胶体粒子间有较强的范德瓦耳斯吸引力,一般为了维持胶体溶液的稳定会在胶体颗粒表面引入电荷或者高分子链防止胶体粒子聚集沉降.严格说,胶体粒子间的相互作用需要考虑到大量原子、离子之间的多体相互作用.但是在很多情况下溶液中的胶体粒子相互作用可以合理简化成相对简单的形式,例如硬球模型、弹性接触模型等,这使得胶体体系的实验观察能够和很多理论模型进行对比.由于胶体溶液的这两个特点,很早就有人开始利用胶体体系作为模型系统来研究凝聚态物理中的一些基本问题,在这一类研究中,大量的胶体粒子被看成“巨原子”在热涨落的驱动下形成各种热力学相(如液体、晶体),通过观测胶体粒子运动的统计行为可以得到各种相的结构和动力学细节,以及系统在不同相之间的转变机制[6−9].

利用胶体体系研究原子/分子系统的相行为,首先需要了解胶体体系的热力学驱动量.在原子系统中,温度T对系统的相行为有决定性的作用.然而,由于胶体粒子尺寸较大,同时受限于胶体溶液的液体环境,在实验室范围内能达到的温度变化对于胶体粒子的热运动影响非常小.在胶体体系中主要的热力学驱动量是熵,下面以最简单的硬球模型为例来理解熵在胶体体系的热力学过程中的作用.首先定义硬球模型中粒子间的相互作用势:

在硬球模型中,粒子间的相互作用势能为零,因此体系的内能U只有粒子动能的贡献(3/2)NkBT,这一项在温度和粒子数一定的情况下为常数.这样体系的自由能F=U−TS由体系的熵S决定.统计上体系的熵取决于体系所能达到的状态数,对硬球体系来说系统状态数正比于体系中的自由空间的大小.胶体体系中自由空间的大小一般用堆积比φ=NVp/V来描述,这里Vp是粒子的体积,V是粒

子充满的空间的体积,N是粒子数.堆积比越低体系的自由体积(或者自由体积密度)越高,相应的熵就越高.这样就能够建立起胶体体系和原子分子体系的热力学相行为的对应关系——胶体体系在低堆积比时的相行为对应原子分子体系在高温时的相行为;胶体体系在高堆积比时的相行为对应原子分子体系在低温时的相行为.通过调节胶体体系的堆积比就能够驱动胶体体系中的热力学相变.

图3给出了理论计算的单分散三维硬球胶体系统的相图,可以看到在堆积比低于0.494时体系处于液体状态,当堆积比高于0.494时体系开始出现结晶,一直到φ=0.74时,体系按照堆积比最高的六角密堆的方式完全结晶.当胶体体系的堆积比由低到高变化时,体系的结构和运动特征也从无序的液体到周期性的晶体变化,对应于平衡态原子体系中温度由高到低的变化.原子材料中的玻璃是通过迅速冷却液体,使其来不及结晶得到的,在胶体体系中也可以使用同样的策略.当胶体溶液的堆积比高于0.494时体系进入过冷状态.由于胶体粒子比原子大得多,其结晶的成核时间也非常长,因此胶体液体很容易达到深过冷状态而不结晶.实验中经常通过增加胶体粒子的不均一度来进一步阻止结晶的发生.过冷液体在φ=0.58左右发生胶体玻璃化转变,φ在0.58—0.64之间为玻璃态.对硬球体系来说,0.64是硬球随机堆积比的上限,对于软球来说这个上限可以更高,甚至超过1.硬球胶体体系的相图在实验上得到了很好的验证.

通过改变堆积比得到的高密度非晶胶体体系就是胶体玻璃.胶体粒子由于尺寸较大,驰豫时间长,能够方便观测,甚至直接利用光学显微镜观察,是研究非晶体系微观结构和运动的理想平台.需要注意的是,胶体玻璃和原子玻璃虽然在很多性质上十分相似,两者之间仍然有很多本质的区别.例如溶液中的胶体粒子的运动是有阻尼的布朗运动,而原子则是在真空环境中运动,因此两者在极短时间尺度上有完全不同的动力学.然而当原子经历大量随机碰撞之后的扩散行为和胶体粒子的扩散没有本质区别.同时胶体粒子之间的相互作用一般比较简单,而且通常是各向同性的球对称的,这与原子系统中的共价键和离子键的相互作用方式有较大的区别,比较接近金属材料中的金属键.通过胶体玻璃得到的结果一般只能得到一些原理性的、普适的规律,而不能对特定的非晶材料进行对应性的定量研究.另外,胶体体系和原子体系非常重要的一点区别是,胶体粒子不满足全同性的假设.胶体粒子一般通过化学合成的方法获得,在合成过程中每个粒子不可能在原子尺度上保持完全一致,而且经常为了便于获得玻璃态会有意使胶体粒子的直径有一定的分布.因此原子体系中基于原子全同性的一些结论,包括量子效应,在胶体玻璃中都不再适用.

图3 硬球体系随堆积比变化的相图实线:平衡态硬球胶体体系相图,随着堆积比的增加体系经历液态、液固共存区到晶体.虚线:非平衡态硬球胶体体系相图,随着堆积比的增加,体系进入过冷液体区,经过玻璃化转变形成胶体玻璃.插图为不同堆积比下胶体体系的共聚焦显微照片[10]Fig.3.Phase diagraMof monodisperse colloidal hard spheres as a function of volume fraction Solid line:Phase diagraMof equilibriuMphase.The systeMevolves froMliquid to crystal with a coexistence region in between.Dashed line:Phase diagraMof non-equilibriuMphases.The systeMevolves froMliquid to glasses through supercooling.The insets are micrographs of colloids at di ff erent packing fractions,obtained by confocal microscopy[10].

1.3 胶体玻璃的主要研究手段

实验上研究胶体玻璃的主要手段包括光学显微实验、激光散射实验以及流变学实验.以下分别对光学显微技术和激光散射技术做简单介绍.

1.3.1 光学显微

微米大小的胶体粒子可以使用现代光学显微镜进行观察.最早的胶体粒子的显微观察可以追朔到布朗发现花粉颗粒的无规则运动.随着实验技术的发展,现代光学显微镜加上数字摄像机能够快速准确地记录胶体粒子运动的图像,实现对胶体玻璃结构和运动的实时观测(图4).光学显微技术有几种常用的观测模式,其中最常用的是明场显微技术.当胶体粒子的折射率与周围的溶剂差别较大时,明场显微镜能够非常清晰地从背景中分辨出胶体粒子.这一技术在胶体粒子排布在同一平面内时尤其方便.当胶体粒子的折射率与溶剂相接近,或者胶体粒子的直径远小于可见光波长时,普通的明场显微方法无法清晰地观察到胶体粒子,这时可以使用荧光显微技术.将荧光染料枝接到胶体粒子上,荧光染料在高频光的激发下发出可见光,使粒子在显微镜下可见.从荧光显微技术发展而来的是扫描共聚焦技术,共聚焦显微镜首先将激发光(通常为激光)聚焦于样品中一点,然后通过共焦面上的针孔将被照射点前后的荧光信号屏蔽,利用探测器实现对三维空间荧光强度的精确测量.通过扫描装置对样品进行逐点扫描可以得到高精度、低噪音的光强空间分布,用于数字重构样品的三维结构,实现对胶体玻璃结构的三维观测[11].理想情况下,如果胶体粒子的折射率和周围溶剂的折射率一致,激发光和荧光信号都能够不受散射沿相同路径传播,获得高质量的三维图象.实验中通常用折射率匹配的方法来接近这一条件.在一些特殊的胶体溶液中,粒子和溶剂之间的折射率能够达到很高的匹配度,使观察上百层的高密度堆积的胶体玻璃成为可能.

图4 现代光学显微视频系统 (a)光学显微镜与视频摄像设备;(b)胶体粒子在显微视频中的图像;(c)粒子跟踪技术对胶体粒子的识别和定位(白色圆圈)Fig.4.Modern video-microscopy system:(a)The optical microscope connected to a CCD camera;(b)an image of colloid particles recorded video microscopy;(c)identi fi cation and locating of colloid particles with particle tracking technique(white circles).

光学显微实验获得的数字图像通过数字图型处理软件进行分析,可以得到粒子的轨迹,常用的方法是粒子跟踪技术(particle tracking).粒子跟踪技术通过分析图片中的亮度分布,可以识别粒子并精确确定粒子的位置坐标(图4(c)).对于高质量的数据,粒子定位的精度可以达到10 nm以下,远远小于光学分辨率,更比粒子本身的直径要小得多,实现对胶体玻璃结构的高精度测量[12].通过连接不同帧之间同一粒子的位置能得到胶体粒子的运动轨迹,这为进一步分析研究胶体玻璃的结构和运动提供了基本数据.光学显微实验得到的粒子轨迹数据在一定程度上兼顾了局部和整体测量的需要.例如,利用胶体粒子位置信息可以直接测出胶体非晶中的结构因子和对关联函数,也可以精确测量和分析各种具体的空间位形.利用粒子的运动轨迹可以计算出单个粒子和体系平均的均方位移(mean square displacement),也可以在实空间内观察不同区域动力学的差异和演化.由于粒子跟踪技术有很高的空间分辨率,即使在动力学很慢的情况下仍然能够测到非晶结构的微小变化,例如在老化过程中的结构驰豫.光学显微方法在非晶结构测量方面的显著优势,是研究非晶中一些基本问题,特别是非晶性质与结构的关联问题的重要方法.

1.3.2 激光散射

光学显微技术能够直接观察胶体玻璃中粒子的运动,然而光学显微镜受视场大小的影响,一般只能同时观察几千到几万个粒子的运动.这虽然能够提供大量的统计信息,但是相比非晶材料中的原子数来说仍然非常小.另一方面,光学显微技术的时间分辨率受摄像设备采集速率的影响,难以捕捉到快速的动力学过程,特别是对200 nm以下的胶体粒子,普通的光学显微镜很难有效观察.这种情况下可以使用动态光散射(dynamic light scattering)来研究.动态光散射的原理如图5所示,由于胶体粒子和溶剂之间有折射率的差异,激光照到胶体粒子上会发生散射,利用探测器可以测量散射光的光强.可以想象,如果胶体粒子保持静止,其散射的光强不会发生变化;当胶体粒子运动时测到的散射光的强度也会随之起伏.通过测量散射光变化的快慢,可以推算出胶体粒子运动的速度,从而获得胶体玻璃中动力学的信息.具体通过测量散射光强度的自关联函数

可以得到胶体玻璃中非常广的时间尺度上的弛豫信息.

除了动态光散射以外,静态光散射可以用于测量胶体玻璃的结构.和X光衍射类似,由于激光的波长和胶体粒子之间的距离接近,可以通过测量不同方向k的散射光得到胶体玻璃的结构因子S(k),通过结构因子可以得到胶体粒子在实空间的位置关联函数g(r).

图5 动态光散射原理[13] 大粒子热运动较慢,其散射的激光光强变化也慢(上图);小粒子热运动较快,其散射的激光光强的涨落也快(下图)Fig.5.DiagraMof dynamic light scattering(DLS)measurements for colloidal particles. The intensity fl uctuation for larger particles is slower due to slow thermal motion(upper panel);for smaller particles,the fl uctuation is faster(lower panel)[13].

2 胶体玻璃在非晶结构研究中的应用

2.1 阻塞相变

非晶结构研究试图回答的一个根本问题是:“在从液体到玻璃转变的过程中,系统的结构有没有发生根本性的变化？”对这一问题的回答除了实验观测之外,更多的需要理论的思考和指导,其中一个理论就是阻塞(jamming)理论.阻塞理论本身并不是针对玻璃建立的理论,而是更为广泛的研究无序体系的相行为的一个框架理论,包括宏观的颗粒体系、胶体体系到原子分子材料[14−16].阻塞理论认为在零温度下,硬球系统的堆积比超过一定阈值时粒子之间会发生从没有接触到接触的转变,同时体系也从不能抵抗剪切的类液状态转变到能够抵抗一定剪切的类固状态.详细的数值模拟研究发现,这一转变过程中观察到很多类似热力学相变的标度关系,因此也称为阻塞相变(jamming transition)[17−19].显然,零温阻塞相变和玻璃化转变前后的情况十分相似,两者最大的区别是玻璃化转变是在非零温条件下发生的.当推广到温度不为零的情况时,阻塞理论认为在无序体系中,温度T,剪切应力Σ和堆积比的倒数1/ϕ在引起阻塞相变过程中起到同等的作用.例如对于一个阻塞(类固)的无序体系,通过升高温度、施加剪切应力或者减小体系的堆积比都能达到去阻塞(unjamming)的效果,使体系呈现出类液的特性.在这个框架下,可以得到一个阻塞相变的相图(图6),利用这个相图有望对广泛的无序体系建议一个统一的描述,因此阻塞理论受到了学术界,包括非晶研究者的重视和研究.

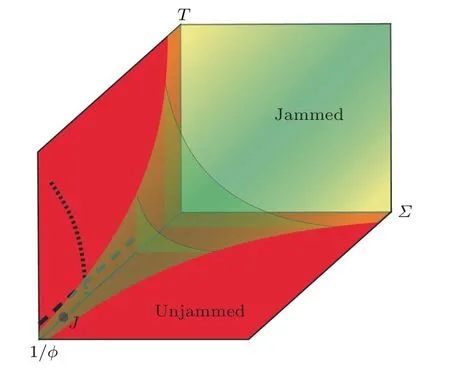
图6 阻塞相图 图中三轴分别为温度T,堆积比的倒数1/ϕ和剪切应力Σ;温度的降低、堆积比增加以及剪切应力减小都能造成无序体系的阻塞转变;图中的J点是零温条件下的阻塞转变点,在非零温情况下,阻塞转变区是相空间中的一个三维曲面[20]Fig.6.The phase diagraMof jamming transition.The 3 axes are temperature T,inverse packing fraction 1/ϕ and shear stress Σ.Jamming transition can occur by lowering the temperature,increase the packing fraction or decreasing the shear stress.Point J in the diagraMis the jamming transition point at zero temperature.When the temperature is not zero,the boundary of the transition is a 3D surface in the phase space[20].

图7 胶体玻璃在阻塞相变附近对关联函数g(r)随堆积比的变化,内插图为g(r)的第一个峰随堆积比的变化[20]Fig.7.The comparison of pair correlation function g(r)of colloid particles with di ff erent volume fraction near jamming transition,the inset shows the evolution of the fi rst peak of g(r)as a function of volume fraction[20].

胶体体系中热运动十分显著,显然是一个非零温体系.为了研究在非零温状态下阻塞相变的结构特征,Zhang等[20]利用温敏性的胶体粒子在准二维情况下测量了胶体玻璃中的对关联函数随着堆积比的演化(图7).研究的关键是如何调节胶体玻璃中的堆积比,Zhang等使用了一种特殊的温敏胶体粒子(聚异丙基丙烯酰胺,PNIPAM).在一定温度范围内,PNIPAM胶体球的直径随着温度的升高而减小,利用这种性质可以通过改变样品温度原位调节胶体玻璃的堆积比[21−23].在胶体玻璃的研究中,原位调节堆积比是一种非常有用的实验手段.因为不同玻璃样品之间很难有完全相同的微观结构,原位调节堆积比能有效排除由于样品的初始构型不同造成的测量差异.在这个实验中,通过观测由两种不同直径的胶体粒子混合形成的二维胶体从液态到固态的演化,研究者发现在阻塞相变点附近系统的动力学急剧变慢,并且空间和时间分布变得十分不均匀,这些特征都符合玻璃化转变的特点.同时,他们还发现胶体玻璃的结构也发生了定性的变化,胶体玻璃的对关联函数g(r)的第一个峰高g1在阻塞转变点附近达到最高值,这表明在阻塞转变后胶体玻璃的结构不只是液体结构的简单冻结和压缩,而是一种新的固体的结构.这一结构特征与同时观测到的系统动力学特征暗示玻璃化转变过程中也可能发生了类似的结构转变.由于g(r)是一个高度平均的结构参数,虽然这一结果并没有指出具体的构型变化,但是为进一步发现玻璃中的特征结构供了一条重要的实验线索.同时,数值模拟表明,g1的峰值在零温情况下是一个发散的峰,这说明实验观察到的g1峰值可以作为非零温条件下阻塞相变的转变点.

2.2 非晶中的结构关联长度

随着对非晶结构研究的深入,人们开始思考非晶看似杂乱无章的结构之间是否存在某种关联.这种论点可以在很多实验事实中得到支持.例如,在玻璃的结构因子测量中发现在对应原子最近邻的峰之前存在一个特征峰,这说明在若干个粒子直径的尺度上存在一些关联结构[24];从热力学的角度看,如果玻璃的结构完全和液体一样,由结构简并度带来的熵将很难维持玻璃的类固体性质.如果玻璃中有较大尺度的相关结构则能解释玻璃化转变过程中的动力学变慢和玻璃的固体特性.研究玻璃中相关结构的一个理论是随机一级相变理论(randoM fi rst-order transition,RFOT)[25,26].这个理论认为在玻璃化转变过程中,液体里产生了一些结构相关的团簇,这些团簇的尺寸随着温度的降低不断增大,使得体系的动力学迅速变慢.这一图像和经典的晶体成核理论十分相似,主要区别是在RFOT理论中生成的团簇不具有周期性的晶体特征.

如何在实验上检验和观测到RFOT理论预言的具有相关结构的团簇一直是非晶研究中的热点.主要困难是非晶中的这类团簇的具体构型并不清楚,因此不能像晶体结构一样“按图索骥”.于是有理论工作者提出了一个新的策略——测量相关结构的尺度[28,29].这个设想假设玻璃中分布着各种大小相近的结构相关团簇,在这些团簇的内部结构是高度相关的,而团簇之间的结构则没有什么相关性,这时候如果将空间中的原子都“冻住”,只留下在一定半径的球体内的原子可以自由运动(如图8所示).当球的半径远大于相关团簇的特征尺寸时,球中心处的粒子的运动并不会受外部粒子冻结的影响,当球的半径接近或小于团簇的特征尺寸时,球中心处粒子的动力学会由于团簇内部的结构相关性而迅速变慢,甚至停止.按照这个方法,原则上可以在不了解团簇的具体构型的情况下,探测团簇的特征尺寸及其随温度的变化.显然,这样的实验在原子非晶里几乎是不可能完成的,因为这需要同时冻结1023数量级的原子的运动,然而在胶体玻璃中,这样的实验是可行的.

在二维的胶体玻璃中,Nagamanasa等[30]利用光镊固定胶体粒子测量了胶体玻璃中相关团簇的特征尺寸随堆积比的演化.当一束激光通过透镜聚焦之后,在焦点附近会产生很强的电场梯度,这种电场梯度能够极化和捕获微小的电介质物体.通过控制激光的位置和强度能够实现对微小物体的操纵和控制,这一技术手段称为光镊(optical tweezer)[31,32].现代光镊通过高速扫描或波前调制的方法可以同时控制成百上千个胶体粒子运动.Nagamanasa等利用多个光镊固定住胶体玻璃中的一部分胶体粒子,在二维胶体玻璃中形成一面“墙”.然后测量“墙”附近的胶体粒子运动受到的影响,发现当样品的堆积比较低时,只有非常接近这面墙的粒子的运动会受明显影响,而当样品的堆积比增加时,墙对粒子运动影响的范围明显增加,这表明与墙的结构相关的团簇的尺寸越来越大.这些团簇的结构关联长度可以通过测量离墙不同距离的粒子变慢的程度来定量获得.图9(c)显示胶体玻璃中的结构关联长度随着样品的堆积比增长,这第一次从实验上证实了RFOT理论的主要论点.

图8 冻结边界法测量非晶中的结构相关长度[27] (a)选取一个平衡的液体构型;(b)冻结在一定范围R之外的所有原子的运动;(c)维持外部原子冻结的条件下观测R内部的不同构型;(d)比较在中心处不同构型之间的差异Fig.8.Probing structural correlation length by freezing boundary in amorphous systems[27]:(a)Pick an equilibriuMcon fi guration;(b)freeze all particles outside of a certain region R;(c)observe di ff erent con fi gurations inside R with the boundary fi xed;(d)compare con fi guration with the initial con fi guration near the center of R.

2.3 胶体玻璃中的结构缺陷

按照随机一级相变理论的物理图象,玻璃中的关联结构可以类比于晶体中的晶畴.晶畴在材料结晶时不断长大,直到不同晶畴之间相互接触成为固体.晶畴内部的结构有很高的相关性,晶畴之间的结构则比较混乱,成为缺陷.按照这个类比,可以推知在玻璃中关联结构团簇之间的区域可能是玻璃中的缺陷.固体中的缺陷除了与背景结构差异之外还有一个有明显的力学特征,即容易发生形变.因此可以通过观测玻璃中局域形变区域来发现非晶中的结构缺陷.发现和识别玻璃中的结构缺陷,不仅有助于理解玻璃的结构特征,而且对于设计和调控非晶材料的力学性能有重要意义.

Yang等[33]研究了胶体玻璃中的局域形变,并分析了这些形变区域的结构,发现胶体玻璃中缺陷区域的结构相关性明显低于背景的结构相关性(图10).Yang等利用双分散的温敏性PNIPAM胶体粒子制备准二维胶体玻璃,胶体溶液中加入了少量红外染料.红外染料吸收可见光后放出红外辐射,实现对样品的局部加热.利用PNIPAM粒子的温敏特性,通过周期性的强光照射可以在胶体玻璃中诱发局域的形变团簇.在这个实验中,诱发局域的而不是大范围的形变对于实验结果的分析十分重要.因为原则上任何形变都有可能造成体系的势能分布发生变化而激发新的形变,形成连锁效应.胶体玻璃中大范围的形变对实验结果的分析造成很大的困难.通过调控样品中的染料浓度和光照强度可以方便地调节局域温度变化幅度,使其刚好能够激发局域的结构变化.

Yang等分析了实验观察到的形变团簇的结构,发现形变区域包含了较多的自由体积(free volume)非常大和自由体积非常小的粒子,这说明在玻璃中极端自由体积的区域都容易发生形变,这对于硬球模型中只有自由体积大的粒子容易发生形变的观点是一个修正.当他们研究另外一个结构参数—局域结构熵S2时,发现S2与局域形变的关联性远高于任何基于最近邻的结构参数.局域结构熵是一个基于局域对关联函数g(r)的物理量,具有熵的量纲,它考虑了粒子周围所有距离上的粒子排布,是一个描述了玻璃中局域结构的无序度的量[34].实验发现,S2高的区域(结构无序度高)比S2低(结构无序度低)的区域发生形变的概率高约两个数量级.在周期性激发的情况下,胶体玻璃中的局域结构熵能够很好地预测形变的发生.因此可以利用S2作为玻璃中的结构参数来判断和识别结构缺陷.这个实验证实了玻璃中存在不同有序度的结构,其中有序度低的区域容易发生形变,这支持了玻璃中可能存在相关结构的猜想.

图10 胶体玻璃的局域形变团簇与结构熵S2[33] (a)胶体玻璃中S2与形变团簇S2的分布;(b)不同S2粒子的形变概率;(c)胶体玻璃中局域形变团簇与S2在空间上的分布Fig.10.Local structural entropy S2and rearranging clusters in colloidal glasses[33]:(a)Distribution of S2for all particles(black squares)for rearranging particles before deformations(red circles)and for rearranging particles after deformations(blue circles);(b)rearranging probability as a function of initial S2;(c)spatial distribution of particle S2and rearranging clusters.

3 胶体玻璃在非晶动力学中的应用

3.1 胶体玻璃化转变

玻璃化转变中动力学急剧变慢的基本机制是非晶物理中的一个核心问题.人们在研究玻璃化转变的过程中发现,在降温过程中过冷液体的黏度或弛豫时间随温度的变化规律并不总是一样的[36,37].对于一些系统,在接近玻璃化转变的过程中液体的黏度变化比较平稳,可以用Arrhenius公式来描述,

这类玻璃称作强性玻璃(strong glass),其弛豫过程可以用一个单一的激活能来描述(图11中的直线).对于另外一类形成玻璃的液体,其黏度在离玻璃化转变温度Tg较远时变化比较慢,随着温度接近Tg,黏度随温度的变化率急剧上升,这类玻璃的黏度对温度极为敏感,因此被称为脆性玻璃(fragile)(图11中的曲线).在这里“强”和“脆”并不是指材料的强度或弹性模量,而是指玻璃状态的稳定性,脆性玻璃的稳定性很容易被很小的温度变化破坏.预测和调控玻璃材料的脆性对于改善玻璃的力学性能有十分重要的意义.然而,人们虽然发现了各种强性和脆性的玻璃体系,但是对于玻璃性质的这种差异并没有明确的物理解释,预测玻璃的强脆特性主要还是依靠一些经验.

图11 不同材料的玻璃化转变曲线[35]Fig.11.Glass transition curves for di ff erent materials[35].

图12 软球和硬球胶体玻璃的结构弛豫与玻璃化转变曲线[38] (a)硬球胶体玻璃的中间散射函数;(b)软球胶体玻璃的中间散射函数;(c)不同硬度的胶体球的玻璃化转变曲线;(d)(c)图中玻璃化转变曲线归一化后的对比图Fig.12. Structure relaxations and glass transitions for both hard and soft colloidal glass[38]:(a)The selfintermediate scattering function for hard colloid particles;(b)the self-intermediate scattering function for soft colloid particles;(c)glass transition curves for hard and soft spheres;(d)same as(c)with volume fraction normalized by glass transition volume fraction.

在胶体玻璃中,玻璃化转变影响因素不再是样品的温度,而是样品堆积比.通过研究胶体玻璃的黏度或弛豫时间随堆积比的变化能得到胶体玻璃的玻璃化转变曲线.其中黏度的一般用流变仪测量,而弛豫时间一般使用光散射的方法得到.需要指出的是,在胶体玻璃化转变过程中黏度或弛豫时间的变化可以达到4—5个数量级,这和原子分子玻璃化转变过程中的12—14个数量级的变化相比非常小.这主要是因为硬球胶体很难达到很高的堆积比,而软球自身的力学模量限制了系统黏度的变化范围.尽管如此,胶体体系在玻璃化转变过程中的实验现象仍然能够为理解玻璃化转变的基本问题提供定性的知识.Mattsson等[38]研究了不同硬度的温敏胶体粒子的玻璃化转变过程(图12),发现软胶体粒子制备的玻璃表现出强性玻璃的特性,硬胶体球制备的玻璃表现出脆性玻璃的特性.

他们通过调节粒子合成过程中的交联剂等因素制备了硬度不同的PNIPAM胶体粒子.由于PNIPAM粒子的温敏性,降低样品温度时堆积比升高,使胶体溶液发生胶体玻璃化转变.这个实验利用动态光散射测量了溶液中胶体粒子的中间散射函数(intermediate scattering function,ISF),通过对ISF的衰减曲线进行拟合获得样品在不同温度下的弛豫时间.图12显示的是不同硬度的胶体粒子的玻璃化转变曲线,这里堆积比在一定程度上对应于原子分子玻璃中温度的倒数1/T.实验结果清晰地表明不同硬度的胶体球有不同的玻璃化转变规律,其中软球胶体体系的弛豫时间在接近玻璃化转变过程中稳定变化,玻璃化转变曲线能够很好地用Arrhenius公式拟合,而硬球胶体体系的弛豫时间随着堆积比的增加变化的速率越来越快,在玻璃化转变附近有急剧增加.虽然这个实验并没有明确解释为什么软球和硬球体系的玻璃化转变过程会有如此明显的差异,Mattsson等的研究为调控玻璃的脆度提供了一条有用的思路,也为理论上解释玻璃的强脆性质提供了新的实验依据.

3.2 非晶中的动力学不均匀性

除了在玻璃化转变过程中的急剧动力学变慢以外,有关玻璃动力学的另一大问题是过冷液体和玻璃中的动力学不均匀性.实验和数值模拟都发现玻璃中不同区域的结构弛豫时间有很大的差异,这与通常认为的玻璃是一种性质均匀的材料的直观印象显然是不符的[39−42].更令人不解的是,玻璃中动力学不仅在空间上不均匀,而且在时间上也不均匀,玻璃中不同区域的动力学快慢会随着时间变化,在这一时刻动力学快的区域在一段时间后会变慢,一些慢的区域会变快.虽然从宏观上看,玻璃的性质十分均匀和稳定,在微观动力学的层次上,玻璃内部似乎非常热闹,不同局部的运动时快时慢.在高温液体中,各处的动力学是十分均匀的,当液体接近玻璃化转变时,动力学不均匀性变得越来越明显.动力学不均匀性是普遍存在于非晶体系中的独特现象,这一现象的微观机制一直是学术界研究的热点问题.

一种非晶中的动力学不均匀性的微观理论是所谓的“协同重排理论”.这个理论认为,当非晶体系的整体动力学随着温度的降低变慢时,玻璃中任何一个粒子要实现大的位移都需要得到周围粒子的“配合”,周围的粒子需要给这个粒子腾出空间,同时这些腾出空间的粒子又需要更多的粒子为它们的位移创造条件.这就像在拥挤的地铁里,如果周围的人都不愿意让开,一个人就很难移动,而下车的时候,当大家都朝一个方向协同运动时就容易多了.过冷液体或玻璃中的任何重排都是以一个协同重排区(cooperatively rearranging regions,CRR)的形式进行的[7].在高温情况下,粒子间的距离较大,只需要最近邻的几个粒子相互协同就能实现较大的位移,在温度较低的时候,需要更多的粒子协同运动,团簇的尺寸也就越大.这造成协同运动变得十分困难,运动发生的频率也越来越低,这反映在动力学测量上就表现出更慢的动力学.

为了检验这一物理图象,Weeks等[43]利用共聚焦扫描显微实验研究了硬球胶体体系中的动力学不均匀性的微观细节.特殊合成的PMMA胶体粒子能够与有机溶液实现良好的折射率和密度的匹配,可以利用激光共聚焦技术观察胶体玻璃的三维结构.随着溶液粒子浓度的增加,体系经历玻璃化转变,从粒子均方位移的测量可以看出,体系的动力学变慢大概两个数量级.Weeks等测量了体系中运动较快的粒子的分布,发现在玻璃化转变过程中体系中运动较快的粒子确实在空间上形成团簇,从而首次从实验上证实了协同重排的图像(图13(a)).随着堆积比的增加,这些团簇的尺寸也不断增加,与体系动力学的变慢同步.同时他们也观察到了快动力学团簇随着时间的不同出现在过冷液体中的不同位置,证实了动力学在时间上也是不均匀的.当体系的堆积比超过玻璃化转变的堆积比后,他们只观察到了一些较小的动力学团簇,这是由于在玻璃化转变之后体系的α弛豫已经超出实验的时间尺度,因此所测量到的动力学团簇反映的是局域的β弛豫过程(图13(b)).共聚焦显微实验能够得到每一个粒子的运动轨迹,通过分析粒子轨迹,他们提出了非晶动力学不均匀性的微观物理图像.实验发现在过冷液体中粒子大部分时间在由自己近邻形成的笼中运动,由于受到笼的限制,粒子的动力学较慢.然而,粒子偶尔能够突破这个近邻形成的笼的束缚,在短时间内实现大的位移,此时粒子表现为快动力学行为.然而很快这个粒子又被新的近邻束缚,动力学重新变慢(图13(c)).这从微观上解释了为什么非晶动力学在空间上和时间上都在不断变化.虽然Weeks等的实验并没有回答非晶动力学不均匀性的起源这一基本问题,但为研究动力学不均匀性提供了直观的实验观察结果,是非晶研究中开创性的经典工作.

图13 硬球胶体玻璃中的动力学不均匀性[43] (a)过冷液体中的快速动力学团簇(大球);(b)玻璃化转变之后的快速动力学团簇(大球);(c)胶体玻璃中粒子的运动轨迹Fig.13.Dynamical heterogeneity in colloidal glasses formed by hard colloid particles[43]:(a)Fast-moving clusters(large spheres)in supercooled liquid;(b)fast-moving clusters(large spheres)in after glass transition;(c)the trajectory of a single particle in colloidal glass,the particle is tracked in 3D,the 2D projection is shown.

3.3 胶体玻璃的老化

由液体快速冷却形成的玻璃的自由能并不是处在体系热力学自由能的最低状态,而是处在一个亚稳态上.因此玻璃在形成之后内部还在不断发生结构的弛豫,玻璃的宏观性质也随着时间在演化,这一过程称为玻璃的老化(ageing)[44−46].经过玻璃化转变之后,体系的动力学已经接近冻结,然而随着老化的时间增加,体系的动力学还会进一步变慢,往往能够发生好几个数量级的变化.与玻璃化转变过程十分类似,在老化过程中玻璃的结构同样没有发现有明显的变化.要了解玻璃老化的微观机制,需要详细测量老化过程中粒子的运动,这在原子分子玻璃中显然十分困难,因此可以利用胶体玻璃来研究非晶的老化过程.

在胶体玻璃中研究非晶的老化也存在一些困难.通常胶体玻璃并不是通过温度的骤降获得的,而是通过改变体系的堆积比来实现的.在常用的硬球体系中,要研究体系在不同堆积比下的行为就需要单独制备不同堆积比的样品.这样的样品在观察时经常已经老化了一段时间,由于老化的动力学是不断变慢的,这时在胶体玻璃中观察到的老化过程已经不明显.为了在胶体玻璃中观测玻璃的老化,需要实现在样品中原位的玻璃化转变,并且在玻璃化转变之后立即对样品进行测量.Yunker等[47]利用温敏的PNIPAM胶体粒子研究了胶体玻璃在老化过程中的动力学和结构演化.由于PNIPAM粒子的直径随着温度的降低而增大,通过调节样品的温度可以实现原位的玻璃化转变.为了避免温度变化过程中的老化,Yunker等利用光加热的方法实现了样品的快速冷却.他们在PNIPAM胶体溶液中加入少量吸光染料,在强光照射下,这种染料能够吸收可见光,放出红外线,从而对样品局部进行加热,使PNIPAM胶体粒子变小,样品由胶体玻璃变为自由扩散的液体.在系统平衡后突然将强光源关闭,被加热区域由于体积很小,温度在0.1 s之内迅速降回室温,粒子直径变大,堆积比上升,系统发生玻璃化转变.玻璃化转变完成后,样品随即进入老化过程,利用显微视频技术能够对样品从液体到老化的全过程进行实时的观察.

Yunker等试图了解玻璃中的局域结构变化和老化过程有什么关联.从系统的均方位移(MSD)的测量发现,老化初期体系的动力学变化最剧烈,随着老化时间的增加MSD的变化也变得越来越慢,微观上表现为体系中的局域重排的发生频率不断下降(图14(a)).非常有趣的是他们发现在老化过程中快动力学团簇,即CRR的平均大小随老化时间变小,这与一般认为动力学变慢与更大的CRR关联的观点矛盾.为了解决这一矛盾,研究者们定义了一种不可逆重组(irreversible rearrangement,IR)[48].在胶体玻璃中,如果一个重组过程让一个粒子永久性的失去3个最近邻,这个重组就被称为不可逆重组.通过分析胶体玻璃在老化过程中的快动力学团簇,发现大部分团簇非常小,只包含几个粒子,有少量的团簇非常大,而这些大的团簇中往往包含经历了不可逆重组的粒子.如果把包含不可逆重组粒子的动力学团簇进行单独分析,发现在玻璃老化过程中这一类团簇在不断长大(图14(b)).从统计物理的角度看,“不可逆”代表了一种自由能降低的过程,因此不可逆重组所形成的局域结构和可逆重组形成的局域结构在自由能上是本质不同的[49].大量的可逆重组形成的小团簇体现的是局域结构的热涨落,而不可逆重组才真正体现了玻璃在老化过程中能量状态的不断降低,以及与之相对应的动力学的持续变慢.

图14 胶体玻璃老化过程中的动力学与结构[47] (a)胶体玻璃老化过程中MSD的变化;(b)胶体玻璃老化过程中快动力学团簇大小的变化,黑色圆圈为所有快动力学团簇,红色圆圈为包含不可逆重排的快动力学团簇Fig.14.The structure and dynamics during ageing in colloidal glasses[47]:(a)Mean square displacement at di ff erent waiting times;(b)the size of fastest clusters as a function of time in aging process,black circles represent the average size of all fast clusters,the red circles represent the average size of the clusters with irreversible rearrangements.

4 胶体玻璃在非晶热力学中的应用

4.1 胶体玻璃中的玻色峰与软模

前面介绍了胶体玻璃在非晶结构和动力学研究中的应用,结构和动力学问题主要关注非晶中粒子的空间分布和运动特点,在这两类问题上胶体玻璃体现出了独特的研究优势,能够在粒子层面上直接观测这两类物理量.在宏观材料中,对于非晶进行的最多的是热力学的测量.热力学关注的是体系内能量的分配和变化,例如通过最简单的比热测量就可得到热能是如何在非晶中各个自由度之间的分配,而材料的弹性模量则反映了单位体积里的弹性能.长期以来,将胶体玻璃应用到非晶的热力学研究存在一个重要的障碍.胶体玻璃一般存在于溶液中,其比热基本上由所在的液体的比热决定.由于胶体粒子比溶液分子大得多(相应的数目少得多),胶体粒子的运动对于胶体溶液的比热影响几乎可以忽略,因此不能通过直接对胶体玻璃溶液进行传统的热学测量来研究非晶的热力学问题.

利用胶体玻璃研究非晶热力学性质的一条途径是研究胶体玻璃中的振动模式.当不考虑量子效应时,在固体中材料的比热基本上由其中的振动模式决定.例如在非晶比热中广泛存在的低温玻色峰就对应着振动态密度在低频段的“过剩”振动模式.而振动模式原则上可以通过分析粒子的运动得到,不需要借助热学测量.因此利用振动模式打开研究胶体玻璃热力学性质的大门一直是学术界研究的一个目标.然而,从胶体粒子的运动中分析出胶体玻璃的振动模式并不是一件直接了当的事,其中主要的问题来自于液体对胶体粒子运动的阻尼.胶体玻璃中的粒子并不是在平衡位置附近做简谐运动,而是在热涨落和溶液阻尼的作用下在平衡位置附近做随机运动.为了消除来自溶液阻尼的影响,Chen等[50]发展了位移协变矩阵分析(displacement covariance matrix analysis)方法,用于分析胶体体系的振动模式.

协变矩阵分析的基本原理如图15所示,在稳定的胶体玻璃中,可以假设每个粒子都在各自的平衡位置附近运动,粒子的平衡位置是粒子势能的局域最低点,任何偏离平衡位置的位形都会造成体系势能的增加.利用玻尔兹曼原理,通过统计粒子在偏离平衡位置不同距离上出现的概率可以刻画出粒子在平衡位置附近的势能面形状,对这个势能面求导可以得到粒子间的相互作用力.利用这种方法测得的势能面的形状只决定于胶体粒子之间的相互作用,与来自于液体分子的阻尼无关.在小位移假设下,粒子间的相互作用可以简化成弹簧连接的简谐相互作用,并建立体系运动方程组,解出胶体玻璃中的本征振动模式[50,56].这样获得的胶体体系的振动模式能够和理论模拟及原子材料中测得的声子模式进行对比.

图15 位移协变矩阵方法原理示意图Fig.15.DiagraMfor displacement covariance matrix analysis.

利用协变矩阵方法,Chen等研究了胶体玻璃的振动态密度和其中软声子模式随着体系堆积比的演化.他们将两种不同直径的温敏胶体粒子混合溶液夹在两片盖玻片之间,形成单层的准二维胶体玻璃.胶体玻璃中不同直径的胶体粒子能够有效防止样品在二维情况下结晶.通过降温增加样品的堆积比得到堆积比大于阻塞点的胶体玻璃.这种高堆积比的胶体玻璃结构十分稳定,在实验时间范围内几乎没有大的结构弛豫,每个粒子可以被认为是在平衡位置附近运动.利用显微视频技术可以获得大量的粒子运动的轨迹,然后通过协变矩阵分析方法得到胶体玻璃的本征频率和本征矢量.Chen等的研究首次在胶体玻璃中观察到了振动态密度的玻色峰,并且发现玻色峰的强度随着堆积比的升高而逐渐减小,同时玻色峰的频率也逐渐向高频移动,这和玻璃材料在加压条件下的振动态密度的变化趋势一致(图16).分析发现,胶体玻璃中的玻色峰主要来自于低频准局域的振动模式的贡献.低频准局域振动模式是一种独特的振动模式,这种模式的振动不再是类似平面波的整体激发,而是由少数粒子主导的一种局部振动模式,也称为软模(soft modes).软模作为一种普遍存在于非晶体系中的振动模式与非晶中的很多现象都有密切的联系,包括非晶中的动力学和局域形变.在这个实验中首次观察到了软模的空间分布特征(图16),证实了胶体玻璃中软模的比例随着堆积比的降低而增加.并且在后续的研究中,Chen等发现胶体玻璃中的软模能够很好地预测局域重排区,能够用于识别玻璃中的结构缺陷[51].协变矩阵的分析方法打开了利用胶体玻璃研究非晶热力学的大门,并且从胶体玻璃扩展到胶体晶体和无热运动的颗粒体系[52−58].

图16 德拜归一化之后的胶体玻璃振动态密度随样品堆积比的变化[50],内插图为软模在空间上的分布,蓝色圆圈处为准局域模式Fig.16.Vibrational density of states normalized by the Debye model as a function of packing fraction[50],inset is spatial distribution of soft modes(blue circles).

4.2 胶体玻璃的弹性模量

协变矩阵方法不仅提供了胶体玻璃中振动频率ω的分布,而且提供了每一个振动模式的本征矢量在空间上的分布.在晶体材料中,振动模式都是平面波,因此每个模式的振动矢量在空间上也是周期性分布的,这一空间周期性可以用一个波矢q来描述.ω关于q的函数称为材料的色散曲线,而色散曲线的斜率就是材料中声波传播的波速[59].宏观上材料的波速取决于材料的弹性模量,因此通过测量体系的色散关系能够推出材料的弹性模量.然而在非晶中,由于结构没有周期性,因此所得到的振动本征矢量在空间上也是无序的,缺乏明显的空间周期性,同时由于频率的展宽,实际测得的本征矢量往往是多个振动模式的叠加.通过测量胶体玻璃的色散曲线计算体系的弹性模量的方法遇到了困难.

图17 胶体玻璃中的色散曲线与弹性模量[60] (a)胶体玻璃中的色散曲线(黑色方块为纵波,红色圆圈为横波),内插图为声速随胶体玻璃堆积比的变化;(b)胶体玻璃中体模量与剪切模量随堆积比的变化Fig.17.Dispersion relations and elastic moduli in colloidal glasses[60]:(a)Dispersion relations in colloidal glasses for longitudinal waves(black squares)and transverse waves(red circles),inset is speed of sound as a function packing fraction;(b)bulk and shear modulus in colloidal glasses as a function of packing fraction.

为了解决这一问题,Still等[60]利用谱函数的方法对胶体玻璃中的振动模式进行了分析,测得准二维胶体玻璃的弹性模量随着体系堆积比的演化.为了得到胶体玻璃中振动模式的空间频率,Still等构造了振动本征矢量的谱函数:

其中fT(q,ω)对应于横波的谱函数,fL(q,ω)对应于纵波的谱函数.谱函数相当于把本征矢量在空间中做傅里叶变换,由于胶体玻璃是各向同性的,因此对同样大小的波矢q在空间中各个方向所得到的结果平均,得到振动模式ω的谱函数.低频振动模式所得到的谱函数有明显的峰值qmax,表明在这些模式中存在着占主导的空间频率.利用胶体玻璃中振动模式的时间ω和空间频率qmax就能得到胶体玻璃中纵波和横波的色散曲线以及相应的声速和弹性模量(图17(a)),这就解决了非晶中振动模式无明显空间周期性的问题.利用这一方法,Still等发现胶体玻璃中的弹性体模量和剪切模量都随堆积比的下降而减少,并且在阻塞相变点附近按照一定的标度律趋近于零(图17(b)).

5 胶体在非晶研究中的展望

作为一个交叉领域,胶体玻璃的研究结合了化学、物理和材料科学的思想和方法.本文通过一些具体的代表性的工作介绍了胶体作为一个模型体系在非晶研究中的特色和最新进展.胶体体系由于其易于观测和调控的优势,特别适合研究非晶物理中的一些基本问题,为建立理论模型和理解原子材料中的实验现象提供一个介观的实验平台.尤其对于非晶中的微观过程,胶体玻璃能够提供目前其他实验手段所难以提供的详细信息.随着实验技术的不断发展,胶体玻璃有望在非晶研究中发挥更重要的作用,其中几个方向值得研究者注意.

1)胶体玻璃中相互作用的精细调控.目前胶体玻璃研究中的粒子之间相互作用还比较简单,主要是以接触为主的硬球相互作用和静电相互作用的短程相互作用,这与实际材料中的各向异性的长程复杂相互作用差别较大.通过设计和调控胶体粒子间的相互作用,特别是原位调控,有可能得到更为接近实际材料的胶体玻璃并发现新的物理规律.

2)高速高通量的观测技术.目前以视频显微技术为主的观测手段数据采集速度仍然较低,特别是对三维胶体玻璃的观测,仍普遍低于常用的视频频率,同时观测的范围也相对较小(大约在1000—10000粒子左右).通过提高数据的采集速率,同时扩展观测样品的尺寸,能够在更大的空间和时间尺度上研究胶体玻璃,这对于具有多时空尺度的玻璃体系来说十分重要.

3)胶体玻璃的主动操控技术.目前主要的胶体玻璃研究关注于观测胶体体系在热涨落驱动下的运动规律.在实际材料研究中有很多主动探测手段,例如力学加载.在胶体玻璃中不仅可以发展类似宏观材料测试中的操控技术,还能利用微操纵手段,如光镊、磁镊以及微机械等技术探索局域加载的实验手段,同时配合相应的显微观测技术将非晶中的宏观和微观性质有效联系起来.

[1]Angell C A,Poole P H,Shao J 1994 Nuovo Cimento D 16 993

[2]Edgerworth R,Dalton B,Parnell T 1984 Euro.J.Phys.5 198

[3]Courtens E,Foret M,Hehlen B,Vacher R 2001 Solid State Commun.117 187

[4]Nakayama T 2002 Rep.Progr.Phys.65 1195

[5]Engberg D,Wischnewski A,Buchenau U,et al.1998 Phys.Rev.B 58 9087

[6]Hiltner P,Papir Y,Krieger I 1969 J.Phys.Chem.73 2386

[7]Kose A Ozaki M,Takano K,et al.1973 J.Colloid.Interface Sci.44 330

[8]Lindsay H,Chaikin P 1982 J.Chem.Phys.76 3774

[9]Pusey P,van Megen W 1986 Nature 320 340

[10]Hunter G L,Weeks E R 2012 Rep.Prog.Phys.75 066501

[11]Prasad V,Smwogerere D,Weeks E 2007 J.Phys.:Condens.Matter 19 113102

[12]Crocker J,Grier D 1996 J.Colloid.Interface Sci.179 298

[13]https://en.wikipedia.org/wiki/Dynamic_light_scattering

[14]Liu A J,Nagel S R 1998 Nature 396 21

[15]O’Hern C,Langer S,Liu A J,Nagel S R 2002 Phys.Rev.Lett.88 075507

[16]O’Hern C,Silbert L,Liu A J,Nagel S R 2003 Phys.Rev.E 68 011306

[17]Ellenbroek W,Somfai E,van Hecke M,van Saarloos W 2006 Phys.Rev.Lett.97 258001

[18]Olsson P,Teitel S 2007 Phys.Rev.Lett.99 178001

[19]Xu N,Vitelli V,Wyart M,Liu A J,Nagel S R 2009 Phys.Rev.Lett.102 038001

[20]Zhang Z,Xu N,Chen D T N,et al.2009 Nature 459 230

[21]Alsayed A M,IslaMMF,Zhang J,et al.2005 Science 309 1207

[22]Han Y,Shokef Y,Yunker P 2008 Nature 456 898

[23]Han Y,Ha N,Alsayed A,Yodh A 2009 Phys.Rev.E 77 041406

[24]Ma D,Stoica A D,Wang X L 2009 Nature Mater.8 30

[25]Lubchenko V,Wolynes P 2007 Annu.Rev.Phys.Chem.58 235

[26]Berthier L,Biroli G 2011 Rev.Mod.Phys.83 587

[27]http://arxiv.org/abs/1311.7142v1[2017-7-1]

[28]Bouchaud J P,Biroli G 2004 J.Chem.Phys.121 7347

[29]Biroli G,Bouchaud J P,Cavagna A,et al.2008 Nature Phys.4 771

[30]Nagamanasa K,Gokhale S,Sood A K,Ganapathy R 2015 Nature Phys.11 403

[31]Ashkin A,Dziedzic J M,BjorkholMJ E,Chu S 1986 Opt.Lett.11 288

[32]Grier D G 2003 Nature 424 810

[33]Yang X,Liu R,Yang M,et al.2016 Phys.Rev.Lett.116 238003

[34]Wallace D C 1987 J.Chem.Phys.87 2282

[35]Angell C A 1985 Relaxation in Complex Systems(Ngai K L,Wright G B,eds.)(US Dept.Commerce.Springfi eld)

[36]Angell C 1995 Science 267 1924

[37]Angell C 2000 J.Phys.:Condens.Matter.12 6463

[38]Mattsson J,Wyss H M,Fernandez-Nieves A,et al.2009 Nature 462 83

[39]Russell E V,Israelo ffN E 2000 Nature 408 695

[40]Kirkpatrick T,Thirumalai D,Wolynes P 1989 Phys.Rev.A 40 1045

[41]Berthier L,Biroli G,Bouchaud J,et al.2011 Dyanmical Heterogeneities in Glasses,Colloids and Granular Media(Oxford:Oxford University Press)

[42]Doliwa B,Heuer A 2000 Phys.Rev.E 61 6898

[43]Weeks E Crocker J C,Levitt A C,et al.2000 Science 287 627

[44]Purertas A 2010 J.Phys.:Condens.Matter 22 104121

[45]Hodge I 1995 Science 267 1945

[46]Kob W,Barrat J L 2000 Eur.Phys.J.B 13 319

[47]Yunker P,Zhang Z,Aptowicz K,Yodh A 2009 Phys.Rev.Lett.103 115701

[48]Widmer-Cooper A,Perry H,Harrowell P,Reichman D R 2008 Nat.Phys.4 711

[49]AdaMG,Gibbs J 1965 J.Chem.Phys.43 139

[50]Chen K,Ellenbroek W G,Zhang Z,et al.2010 Phys.Rev.Lett.105 025501

[51]Chen K,Manning M,Yunker P,et al.2011 Phys.Rev.Lett.107 108301

[52]Yunker P,Chen K,Zhang Z,et al.2011 Phys.Rev.E 83 011403

[53]Chen K,Still T,Schoenholz S,et al.2013 Phys.Rev.E 88 022315

[54]Yunker P,Chen K,Zhang Z,et al.2011 Phys.Rev.Lett.106 225503

[55]Tan P,Xu N,Scho fi eld A,et al.2012 Phys.Rev.Lett.108 095501

[56]Brito C,Dauchot O,Biroli G,Bouchaud J P 2010 Soft Matter 6 3013

[57]Valenza J,Johnson D L 2012 Phys.Rev.E 85 041302

[58]Shen H,Tan P,Xu L 2016 Phys.Rev.Lett.116 048302

[59]Aschcroft N,Mermin N 1976 Solid State Physics(Harcourt)

[60]Still T,Goodrich C,Chen K,et al.2014 Phys.Rev.E 89 012301

PACS:82.70.Dd,61.43.Fs,71.55.JvDOI:10.7498/aps.66.178201

Applications of colloids in glass researches∗

Chen Ke†

(Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China)

3 July 2017;revised manuscript

8 August 2017)

As a soft matter material,the unique properties of colloidal glasses make it a particularly useful platforMto study fundamental physics of amorphous solids.In the article,we brie fl y review the connections between colloidal glasses and molecular amorphous materials by surveying applications of colloids in di ff erent aspects of glass researches.And we also give future directions of colloidal glasses researches in the end.

colloids,glasses,amorphous solids

10.7498/aps.66.178201

∗国家重点基础研究发展计划(批准号:2015CB856800)和国家自然科学基金(批准号:11474327)资助的课题.

†通信作者.E-mail:kechen@iphy.ac.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Basic Research PrograMof China(Grant No.2015CB856800)and the National Natural Science Foundation of China(Grant No.11474327).

†Corresponding author.E-mail:kechen@iphy.ac.cn