输入电流连续型Buck变换器拓扑关联问题探析

吴红飞， 邢 岩

(南京航空航天大学 自动化学院， 江苏 南京 210016)

输入电流连续型Buck变换器拓扑关联问题探析

吴红飞， 邢 岩

(南京航空航天大学 自动化学院， 江苏 南京 210016)

本文探析了输入电流连续型Buck变换器拓扑族之间的内在关联，建立了Buck变换器的统一数学模型，并深入分析和对比了各Buck变换器的控制和纹波特性等。本文有助于学生更加深入地理解不同形式的Buck变换器拓扑之间的内在联系及其特性，具有一定的教学指导意义。

Buck变换器；电路拓扑；电流连续；耦合电感

0 引言

随着电力电子技术的发展以及应用领域的不断扩展，“电力电子技术”课程的重要性和基础性日益突显，并且在“电力电子技术技术”课程基础上发展出了包括“开关电源技术”、“航空航天供电系统”、“新能源发电技术”等一系列后续相关课程[1,2]。Buck变换器作为最基本、最典型的电力电子变换器拓扑，在各类功率变换系统中具有非常广泛的应用，在上述课程中均会有所涉及[3]。

除了经典的Buck变换器外，还包括面向新能源发电、航空航天供电等系统应用的输入电流连续型Buck变换器，例如带输入LC滤波器的Buck变换器、SuperBuck变换器等衍生拓扑[4-6]。但是，这些输入电流连续型Buck变换器拓扑通常都是直接给出的，在现有的教学资料中对于它们之间的内在联系、特性的异同以及各自的适用场合等均缺乏系统全面的阐释。笔者在教学过程中发现，分别独立地讲解每个变换器的拓扑构成、工作原理和特性很难使学生深刻理解该类输入电流连续型Buck变换器拓扑族背后所隐藏的内在规律，无法从系统层面和方法论的角度理解所学内容，更不能做到触类旁通。

笔者结合教学和研究实践，以耦合电感Buck变换器为基础，揭示了输入电流连续型Buck变换器之间的内在联系，指出了它们分别是耦合电感Buck变换器在不同耦合系数情况下的特例，不同的特例导致了不同电路形式的Buck变换器的小信号模型、纹波、电流应力等特性的不同。

1 拓扑推导

图1所示为耦合电感Buck变换器，其中，为了实现输入电流连续引入了输入滤波电感Lin，Lin和输出滤波电感Lo反向耦合，M为互感。图2给出了耦合电感Buck变换器拓扑等效变换的详细过程：图2(a)在图1的基础上将耦合电感等效连接到电源负端；图2(b)将耦合电感用等效电路代替；图2(c)则在图2(b)的基础上将电源负端的两个电感等效连接到电源正端，即最终得到的耦合电感Buck变换器的等效电路如图2(c)所示。

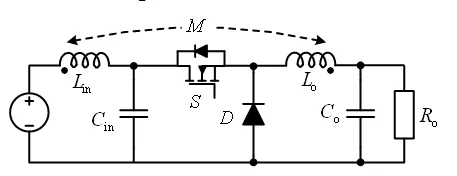
图1 耦合电感Buck变换器拓扑

(a)耦合电感连接到电源负端

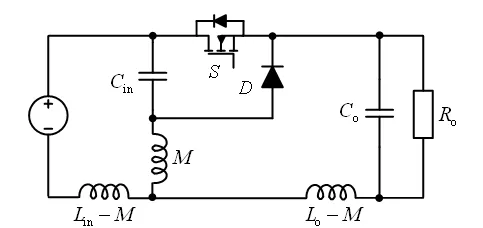
(b)耦合电感等效变换

(c)电感连接到电源正端图2 耦合电感Buck变换器拓扑等效变换

图2(c)中三个电感满足以下关系：

(1)

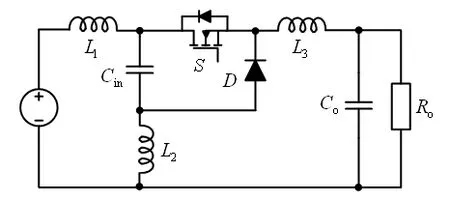
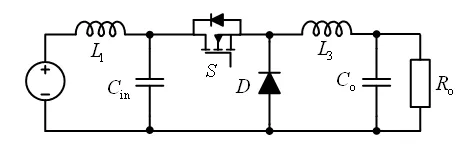
根据式(1)和图2(c)可知，若互感M=0，则电路可以简化为图3(a)所示；若互感M与输入电感Lin相等，则图2(c)中L1=0，此时电路可以简化如图3(b)所示；若互感M与输出电感Lo相等，则此时电路可以简化为图3(c)所示。图3(b)及(c)所示电路即文献中所研究的两种SuperBuck变换器。

(a)第一种Buck拓扑

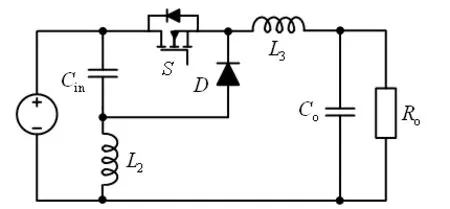
(b) 第二种Buck拓扑

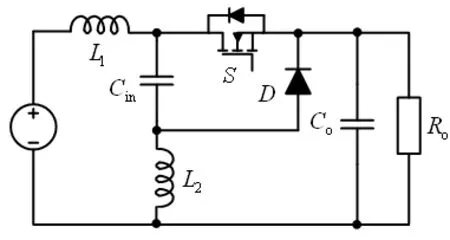
(c)第三种Buck拓扑图3 电流连续型Buck变换器

上述分析表明，传统带输入LC滤波器的Buck变换器以及SuberBuck变换器等几种输入电流连续型Buck变换器实际上都是图1耦合电感Buck变换器不同耦合系数下的特例，它们可以由图1或者图2(c)所示电路统一表示。因此，可以利用统一电路模型对几种电路的特性进行统一分析。

2 电路拓扑特性分析

2.1 控制特性

采用状态空间平均法，首先建立图2(c)所示统一电路的控制到输出的传递函数Gvd(s)[7]。如式(2)所示，式中DS为开关管稳态占空比，Vin为输入电压。基于式(2)，分别令L1、L2或L3为0，就可以直接得到图3所示三种Buck电路控制到输出的传递函数，如式(3)～(5)所示。

由式(3)～(5)对比可以发现，三种输入电流连续型Buck变换器在控制特性上的主要差异体现在

(2)

(3)

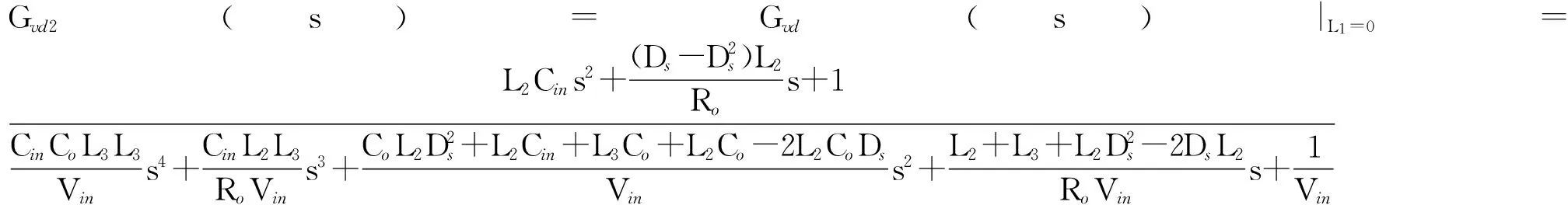
(4)

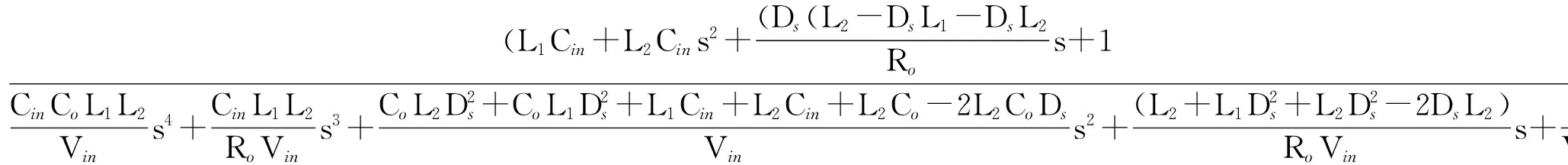
(5)

传递函数的分子上。根据劳斯-霍尔维茨定理，函数在右半平面没有零点的充要条件为转移函数分子的各项系数均为正。根据式(3)可知，图3(a)所示第一种Buck变换器的控制到输出的传递函数中一定存在右半平面零点；由式(4)可知，图3(b)所示第二种Buck变换器一定不存在右半平面零点；由式(5)可知，图3(c)所示第三种Buck变换器的右半平面零点取决于占空比和电感的关系：当(L2-DSL1-DSL2)<0时其存在右半平面零点，当(L2-DSL1-DSL2)>0时则不存在。对于开关变换器而言，右半平面零点通常会在负载跃变或输入电压阶跃时引起输出宽带的振荡[7]。因此，从消除右半平面零点、改善系统控制性能的角度，图3(b)和(c)两种Buck变换器更有优势。这也是SuperBuck变换器在航空航天等应用场合受到更多关注的原因之一。

2.2 电流应力与纹波特性

三种电流连续型Buck变换器开关管和二极管的电压电流应力均相等。下面主要对比分析各Buck变换器中滤波电感的电流应力及输入输出电流纹波，对比分析结果如表1所示。其中Io为输出电流平均值，Vo为输出电压，Ts为变换器开关周期，ΔVCin为输入电容电压纹波。从表1可以看出，输入输出参数相同时，因为输入电容电压纹波ΔVCin远小

表1 电流应力及纹波比较

于输入电压Vin和输出电压Vo，第一种Buck变换器输入输出电流纹波最小，第三种Buck变换器的输入输出电流纹波最大，第二种Buck变换器的输入输出电流纹波则介于两者之间。在滤波电感电流应力方面，流过电感L1和L3的平均电流分别等于输入和输出电流平均值，而流过电感L2的平均电流与开关管占空比DS有关，若DS>0.5，则IL2IL1。因此，从减小电感电流应力的角度，第二种Buck变换器适用于DS>0.5的应用场合，而第一种Buck变换器则更适合DS<0.5的应用场合。而为了实现相同的输出电流纹波，第三种Buck变换器的滤波电感值则要较其它两种Buck变换器的电感值大很多。

3 实验验证

为验证上述分析，搭建了图3(a)和图3(b)两种电流连续型Buck变换器样机，样机参数：输入电压Vin=50～60 V，输出电压Vo=42 V，输出功率Po=500 W，开关管：IPA030N10N3，二极管：V30100SG，L1=L2=20 μH，L3=70 μH，Cin=33 μF,Co=470 μF，开关频率fs=50 kHz。需要注意的是，虽然第一种Buck变换器的电感L1和第二种Buck变换器的电感L2感值相同，但是流经L1的电流远大于流经L2的电流。

图4为图3(b)所示Buck变换器在Vin=55 V 时的稳态工作波形，从中可以看出流经滤波电感L2的平均电流为2.8 A，流经滤波电感L3的平均电流为12 A，与表1中的分析结果一致。

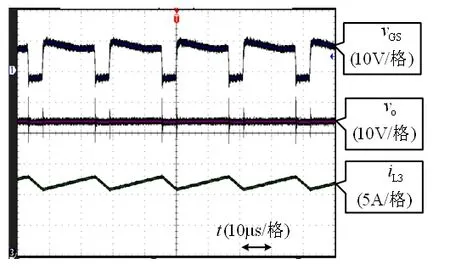
(a)驱动电压VGS、输出电压Vo和电流IL3

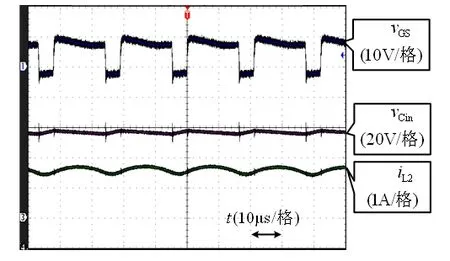
(b)驱动电压VGS、电容电压VCin和电流IL2图4 Buck变换器稳态实验波形

图5给出了第一种和第二种Buck变换器突卸负载的实验结果。从图中可以看出，在所有参数都相同的情况下，当负载由满载到20%负载阶跃时，图3(b)所示第二种Buck变换器电压超调更小、恢复时间更快，表明其具有更好的动态性能，与理论分析一致。

4 结语

本文揭示了几种输入电流连续型Buck变换器的内在联系，分析表明三种Buck变换器均可由耦合电感Buck变换器推导得到。本文分析了几种电流连续型Buck变换器的控制特性、电流应力和纹波特性，给出了各Buck变换器的适用场合，并进行了实验验证。本文有助于学生深入掌握电流连续型Buck变换器拓扑的内在联系和特性，了解拓扑族背后所隐藏的构成规律，可以更加针对性的根据具体应用场合和参数选择合适的拓扑结构，也可以将Buck拓扑分析方法应用于Boost等其它变换器拓扑族的分析。

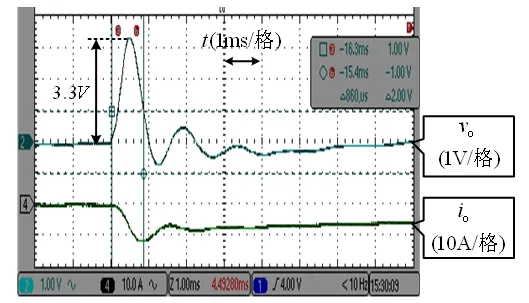
(a) 第一种Buck变换器

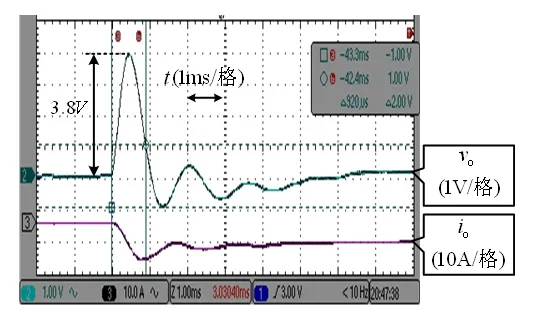
(b) 第二种Buck变换器图5 满载到20%负载阶跃实验波形

[1] 杨善水, 王莉, 张卓然. “航空航天供电系统”的课程改革研究[J]. 南京：电气电子教学学报, 2012, 34(1):19-20.

[2] 陈杰，秦海鸿，龚春英，刘闯. “新能源发电技术”课程建设与教学改革[J]. 南京：电气电子教学学报, 2015, 37(2): 28-30.

[3] 陈骞，郑琼林，李艳. 航天用带耦合电感的电流连续型推挽类拓扑研究[J]. 北京：电工技术学报, 2014, 29(10): 1-11.

[4] 朱成花，石健将，严仰光. 直/直变换器输入滤波器的设计[J]. 北京：电工技术学报, 2004, 19(1): 85-91.

[5] 贾鹏宇, 郑琼林, 李艳. Superbuck电路的稳定性分析[J]. 北京：电工技术学报, 2013, 电工技术学报, 2013, 28(1增):480-487.

[6] 张国帅, 雷卫军, 郑岩,陈永刚, 万成安. 基于Superbuck拓扑的高效蓄电池充电调节器研究[J]. 天津：电源技术, 2015, 39(9):1937-1940.

[7] 张卫平. 开关变换器的建模与控制[M]. 中国电力出版社, 2008.

Intrinsic Relationship Among Continuous Input-Current Buck Converters

WU Hong-fei, XING Yan

(CollegeofAutomationEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China)

The intrinsic relationship among continuous input-current Buck converters is revealed. The unified mathematical model of these Buck converters is built. The control characteristic, ripple currents and current stresses of filters are analyzed in detail. It can help students to understand the intrinsic topological principles and characteristics of Buck converters thoroughly, which has certain significance for the education of power electronics.

Buck converter; circuit topology; continuous current; coupled-inductor

2016-08-26;

2017-02- 08

吴红飞(1985-)，男，博士，副教授，主要从事电力电子与电力传动相关的教学与科研工作，E-mail: wuhongfei@nuaa.edu.cn

TM46, G642

A

1008-0686(2017)04-0097-04