静磁场交界面条件应用教学研究
2017-09-08谢宝昌
谢宝昌
(上海交通大学 电子信息与电气工程学院, 上海 200240)
静磁场交界面条件应用教学研究
谢宝昌
(上海交通大学 电子信息与电气工程学院, 上海 200240)
交界面条件是“电磁场”教材的重要内容。本文针对静磁场交界面条件应用教学过程中发现的具有非光滑边界同轴问题,深入探讨交界面上磁介质产生的磁化面电流分布,提出交界面条件只适用于交界面光滑的场合。非光滑交界面问题需要全面检验交界面条件,只有满足麦克斯韦方程组和边界条件时才能利用矢量场唯一性定理说明解是正确的。
静磁场; 交界面条件; 磁化电流
0 引言
交界面条件是“电磁场”课程的重要内容之一,主要是应用场矢量的积分方程推导出交界面两侧场矢量应满足的关系,即用场矢量闭合回路线积分方程确定其切向分量的连续性,用场矢量闭合曲面积分方程确定其法向分量的连续性。
本文针对静磁场矢量交界面条件应用教学过程中出现的问题,深入探讨磁介质中的磁化电流,提出交界面条件只适用于光滑边界(单位法矢量函数连续),对于非光滑边界则需要仔细检验解的正确性。
1 静磁场交界面条件应用一题[1-3]
设同轴电缆内导体半径为a,外导体是内、外半径分别为b和c的圆筒。内、外导体间填充磁导率分别为μ1和μ2的两种不同磁介质,如图1所示,计算同轴电缆电流为I时的磁场和单位长度电感。
2 典型解法[2,3]
典型解法假设磁感应线是同轴圆,两种磁介质交界面上磁感应强度连续,根据安培环路定律同轴电缆外部磁场为零,内部各区域内同轴圆环上的磁感应强度连续。

图1 同轴电缆
在圆柱坐标系中表示为
(1)
式中,B为磁感应强度矢量,μ0为真空磁导率,aφ为周向单位矢量。
利用能量法可以进一步计算单位长度的电感
(2)
3 典型解法存在的问题与原因分析
两种介质交界面上传导电流面密度Js由交界面两侧的磁场强度H1和H2的切向分量确定:
Js=an×(H1-H2)
(3)
其中,交界面单位法矢量an由介质2指向介质1。
在r=a的交界面上,由式(1)和式(3)得到传导电流面密度Js1:
(4a)
类似地,在r=b的交界面上,传导电流面密度Js2:
(4b)
其中,J01=I/2πa,J02=I/2πb,sgn(·)为符号函数。
在φ=0和φ=π的交界面上,因假设磁感应强度只有法向分量,既没有传导电流面密度也没有磁化电流面密度。对于常规导体,恒定电流密度均匀分布,同轴电缆导体表面不可能存在传导面电流。如果式(4a)和式(4b)成立,那么在φ=0和φ=π的交界面上将产生切向磁场。这与假设磁场只有法向分量是矛盾的。
尽管各交界面上磁感应强度的法向分量都连续,但典型解法存在的主要问题是在r=a和r=b的圆柱交界面上磁场强度切向分量不连续。
同轴电缆内、外导体电流密度均匀分布,具有轴对称性,外导体电流在磁介质和内导体空间不产生磁场,因此使磁介质磁化的外部磁场由内导体电流产生。磁介质被磁化过程中,磁化电流在空间还会产生一个附加磁场,该附加磁场对磁介质进一步起磁化作用。内导体电流在磁介质中产生的磁场强度为
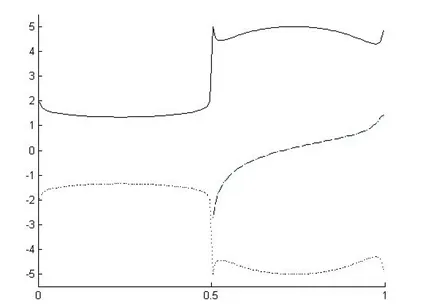
H=aφJ01a/r, a (5) 圆柱交界面上磁介质不均匀,式(5)磁场引起的交界面r=a和r=b上磁化面电流密度Jms分别为 Jms11=az(μr1-1)J01,r=a,0<φ<π; (6a) Jms12=az(μr2-1)J01,r=a,0<φ<2π; (6b) Jms21=az(1-μr1)J02,r=b,0<φ<π; (6c) Jms22=az(1-μr2)J02,r=b,π<φ<2π; (6d) 利用叠加原理可以计算磁化面电流引起的附加磁场,同一圆柱面上的磁化面电流因磁介质相对磁导率不同而不同,因此磁化电流不仅在磁介质中产生附加磁场,而且引起交界面φ=0和φ=π上产生切向磁场分量并形成磁化面电流,同时圆柱面上又附加新的磁化电流面密度的分布,这个耦合磁化过程很复杂。 由于传导电流位于非磁性材料区域,因此相对磁导率为常数的磁性材料中磁化电流体密度为零,只有各磁介质交界面上存在平行z轴方向的磁化电流面密度。设半径为a的圆柱面上磁化电流面密度为Jms1(φ),其中上、下半圆柱面分别为Jms11(φ)和Jms12(φ);半径为b的圆柱面上磁化电流面密度为Jms2(φ),其中上、下半圆柱面分别为Jms21(φ)和Jms22(φ);两种磁介质的两个交界面φ=0和φ=π上磁化面电流密度分别为Jms3(r)和Jms4(r)。空间矢量磁位以轴线r=0处为零,可以用垂直轴线平面内的传导电流面积分和磁化电流线积分表示空间任意点的矢量磁位[4]: (7) 其中,S为平面内传导电流体密度J所在面域,l为平面内磁化电流面密度Jms所在线域,r和s分别为空间场点和源点矢量。 磁感应强度等于矢量磁位的旋度,而矢量磁位只有z轴分量且仅仅与圆柱坐标变量r和φ有关,于是: (8) 将矢量磁位表达式(7)代入式(8)后得到 (9) 同轴电缆外导体电流在磁介质内部不产生磁场,磁化面电流与外导体电流密度无关,当a (10) 由于任意两种介质交界面上只有磁化电流面密度而没有传导电流面密度,因此交界面两侧的磁场强度切向分量和磁感应强度的法向分量连续,磁感应强度切向分量满足 an×(B1-B2)=μ0Jms (11) 另一方面,交界面上磁化电流面密度可由磁化强度矢量M计算,磁化强度与磁感应强度满足 M=(μr-1)B/μ (12) 磁性与非磁性介质交界面上的磁化电流面密度为 Jms=M×an (13) 其中,交界面单位法矢量an由磁介质指向外部非磁性介质。 设图1中相对磁导率为μr1和μr2磁介质中的磁感应强度分别为B1和B2,在r=a和r=b的交界面上由式(12)和式(13)分别得到 Jms11=ar×(μr1-1)(B1/μ1)|r=a,0<φ<π; (14a) Jms12=ar×(μr2-1)(B2/μ2)|r=a,π<φ<2π; (14b) Jms21=ar×(1-μr1)(B1/μ1)|r=b,0<φ<π; (14c) Jms22=ar×(1-μr2)(B2/μ2)|r=a,π<φ<2π; (14d) 在φ=0和φ=π的交界面上,由式(11)分别得到 Jms3=aφ×(B1|φ=0-B2|φ=0)/μ0,a (14e) Jms4=aφ×(B2|φ=π-B1|φ=π)/μ0,a (14f) 将式(10)分别代入(14a)~(14f)后得到各交界面磁化电流面密度满足的强耦合积分方程: (15a) (15b) (15c) (15d) (15e) (15f)(谢宝昌文) 由式(15a)~(15f)可知,只有当两种磁介质的相对磁导率满足μr1=μr2时,交界面上的磁化面电流Jms3和Jms4为零,圆柱面r=a和r=b上的磁化面电流均匀分布且满足式(6a)~(6d) ,磁感应强度由式(1)确定。 由于无法获得磁化电流面密度的简单解析解,也不能利用分离变量法获得无穷级数解,为此利用数值积分方法进行离散化求解。计算参数如下μr1=2,μr2=10,b/a=2,结果如图2所示,纵坐标磁化面电流密度经过归一化处理,其中实线Jms1/J01,点线Jms2/J02,横坐标1代表2 ;虚线Jms3/J01和Jms4/J01的横坐标0.5代表r=a而1代表r=b。归一化处理后磁介质内、外两个圆柱面上相同角度 处磁化面电流密度的大小相同,方向相反,但非均匀分布,在磁介质分界面φ=0和π处发生突变。在磁介质分界面φ=0和 处的磁化面电流分布不仅大小而且方向也发生变化。 图2 归一化磁化面电流密度分布 进一步研究发现,当两种磁介质(μr-1)/(μr+1)的值越接近,圆柱面上磁化面电流分布越均匀,μr的值越大则归一化幅值越大;当两种磁介质(μr1-μr2)/(μr1+μr2)的值越接近零,则分界面φ=0和π处的磁化面电流分布越接近零。 本文根据静磁场交界面条件应用教学过程中发现的问题,深入探讨了磁介质中磁化电流的分布,提出了应用交界面条件的前提条件是交界面必须是光滑的。存在非光滑交界面时,需要全面检验交界面条件,只有场量满足场方程和边界条件时才能利用矢量场唯一性定理说明解是正确的。 [1] 周希朗. 电磁场与波基础教程[M]. 北京:机械工业出版社,2014年 [2] 马西奎. 电磁场要点与解题[M]. 西安: 西安交通大学出版社,2006. [3] 海欣. 电磁场与电磁波学习及考研辅导[M]. 北京: 国防工业出版社,2008. [4] 谢宝昌. 电磁能量[M]. 北京:机械工业出版社,2016年 Research on Boundary Condition Application Teaching of Magneto-Static Field XIE Bao-chang (SchoolofElectronicInformationandElectricalEngineering,ShanghaiJiaoTongUniversity,Shanghai200240,China) Boundary conditions are significant content of Electromagnetic Field. The problem of coaxial cable is found when boundary conditions are applied to solve magneto-static field with unsmooth boundary. Therefore, further investigation is made to find the magnetized current distribution in magnetic media. Premise of smooth boundary is proposed to properly use boundary conditions. All boundary conditions must be checked in solving problems with unsmooth boundary. Only when the solution satisfies the Maxwell equations and the boundary conditions, could it be validated by the theorem of uniqueness of vector field. magneto-static field; boundary conditions; magnetized current 2016-06-23; 2016-12-20 谢宝昌(1965-),男,博士,副教授,主要从事电机与电器的教学与研究工作,E-mail:bcxie@sjtu.edu.cn TM153 A 1008-0686(2017)03-0021-044 磁介质中磁化电流分布
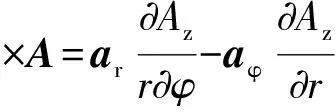

5 结语
