面向微小卫星的星敏感器研究*
2017-09-08金仲和王本冬
李 赓,王 昊,金仲和,王本冬
(浙江大学航空航天学院,杭州 310027)
面向微小卫星的星敏感器研究*
李 赓,王 昊*,金仲和,王本冬
(浙江大学航空航天学院,杭州 310027)
研制了一款新型面向微小卫星的星敏感器,采用商用器件构成以满足微小卫星对小型化的要求。星敏感器由工业镜头、DSP、低功耗CPLD和灰度型CMOS图像传感器组成。为进一步提高测量精度以满足卫星的需求,针对星敏感器的成像模型进行了分析,并用恒星校准的方式补偿了光学参数;对恒星处理算法进行了分析,在图像处理环节特别地采用了中值滤波技术,解决了孤立脉冲噪声对星点提取的影响。基于地球自转的星座跟踪实验表明,所研制的星敏感器样机欧拉角回归标准差为30″,已可实际应用于微小卫星平台。
星敏感器;微小卫星;姿态确定
微小卫星逐渐开始在各个行业展开应用,承担起大卫星的任务,其巨大的应用价值和潜力被航天业极为重视。微小卫星追求更小的体积,更轻的重量,以便缩减研制成本、减少发射周期。相比过去大卫星,微小卫星采用商用器件,成本优势较为突出,一般可减少一到两个数量级的预算开销。然而,许多卫星任务必须建立在姿态稳定的前提下,典型微小卫星ZDPS-2[1]3σ姿态控制精度为5°,其精度受限于太阳敏感器[2]和磁强计的误差,且缺少大卫星中普遍采用的高精度星敏感器。然而从整体行业来看,目前鲜有微小卫星可以满足高分辨率成像和高带宽通信等这类对姿态精度要求较高的任务[3-4]。微小卫星未来要应用到更多空间任务,以微型化星敏感器提高姿态测量精度是必然趋势[5]。
星敏感器作为航天器、飞行器、船舶等载体姿态确定和方位导航的重要视觉测量仪器,在所有已知姿态确定仪器中具有最高的角秒级(1/3 600°)精度。虽然星敏感器发展至今越来越成熟,被成功应用至各类宇航任务,但是大多数配置于大型卫星。微小卫星对星敏感器的电压、功耗、体积和重量要求都比较严苛。目前美国洛克希德马丁公司研制的星敏感器AST-301[6]具有业界最高的测量精度,X/Y轴精度0.18″,Z轴精度5.1″,但是质量高达7.1 kg。此外,以SED36、HYDRA[7]为典型代表的星敏感器指标都与微小卫星要求的相去甚远。
为此浙江大学自主研制了一款面向微小卫星的星敏感器硬件平台[8],然而其实际测量精度与预期相差甚远。本研究在该平台基础上重点解决了微型化过程中面临的两个关键问题:基于模型分析了误差来源并实现了补偿;设计了外场测试实验并进行了精度验证。
1 系统设计
相比已有的大型星敏感器,微小卫星可用的资源有限。浙江大学自主研制的星敏感器采用了商用化机器视觉镜头、图像传感器和处理电路,确保在体积、功耗降低前提下,同样拥有高速的运算能力,实现复杂算法和软件,样机实物如图1所示,结构如图2所示。该星敏感器样机重量150 g,总功耗1.6 W,体积97 mm×73 mm×50 mm,理论单星最优测量精度为4″(X/Y)/25″(Z),其系统框图示于图2。

图1 星敏感器样机
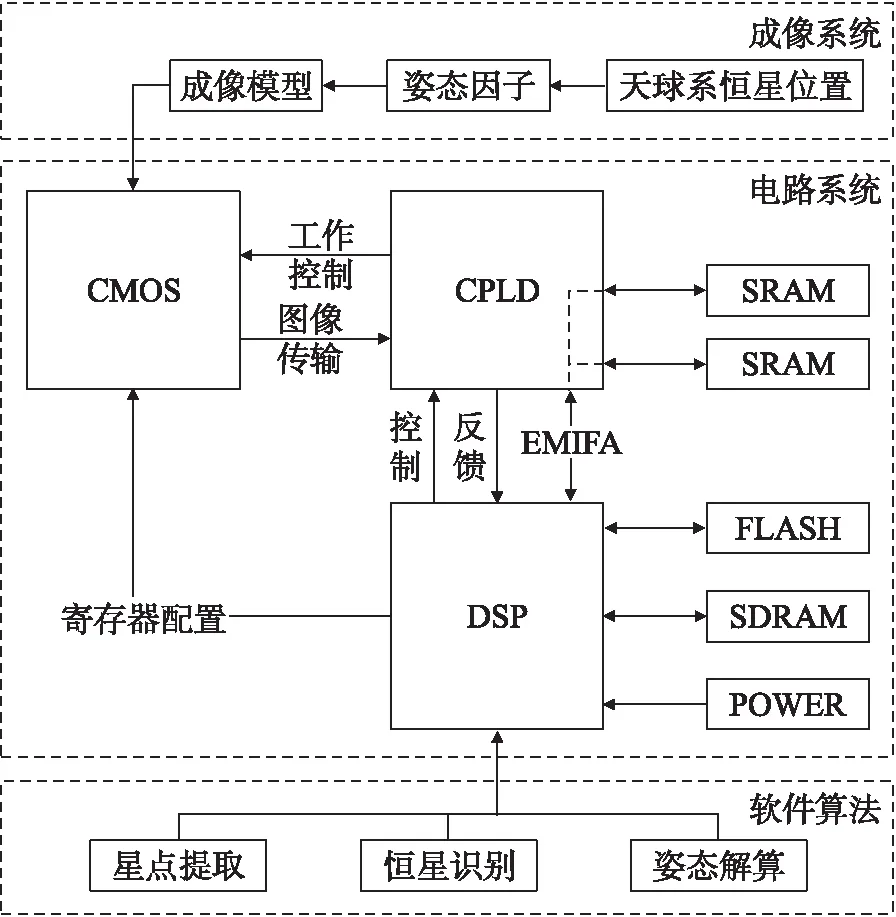
图2 系统框图
然而样机的实测精度无法达到实用标准,为此本研究从系统结构分析出发,通过建模补偿的方式提高样机的测量精度。
星敏感器采用的是通用的商业部件模块化结构,下面首先分别对各个组成模块进行简要说明。
1.1 成像系统
样机采用的商用化工业机器视觉镜头如图3所示,有效缩减了传统星敏感器花在光学部件的体积和成本。相机安装遵守C型标准法兰距(Flange Back Focal Length)保证镜头对焦面与CMOS工艺面高度重合,解决未补偿下过大的几何工装误差问题。与光学部分配套的CMOS图像传感器采用商用化ON Semiconductor系列,从像元尺寸、填充率以及感光度上解决了星敏感器在体积、功耗和探测能力、探测精度的矛盾关系。整体成像系统的关键参数如表1所示。

图3 光学镜头
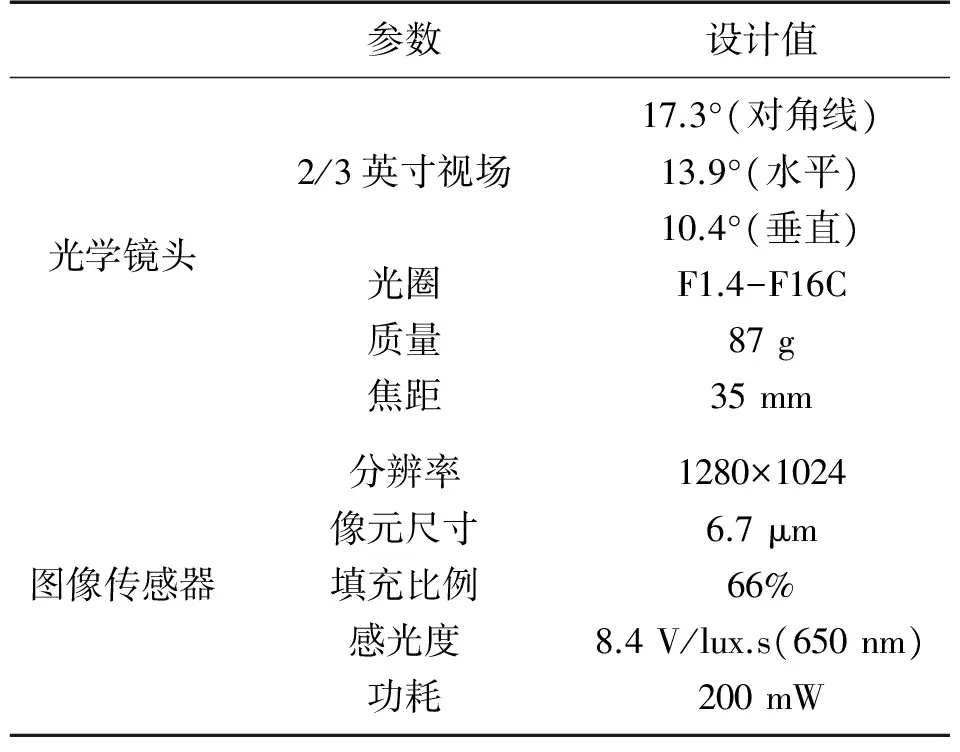
参数设计值光学镜头2/3英寸视场光圈质量焦距17.3°(对角线)13.9°(水平)10.4°(垂直)F1.4-F16C87g35mm图像传感器分辨率像元尺寸填充比例感光度功耗1280×10246.7μm66%8.4V/lux.s(650nm)200mW
1.2 电路结构
星敏感器的架构如图2所示。系统以低功耗、速度较快的TI系列DSP作为主处理器,结合功耗较低的可编程器件CPLD、CMOS图像传感器,共同构成适用于微小卫星的电路与系统。
DSP负责图像处理、恒星识别以及姿态计算。CPLD采用XilinxCoolRunnerII系列,功耗比FPGA低一到两个数量级,系统结构精简,负责辅助驱动CMOS以及控制图像流。
星敏感器单帧图像数据流始于DSP的拍照信号,CPLD内设计的状态机负责驱动CMOS的成像和SRAM的存储调度。而DSP内部的EMIF(External Memory Interface)通过CPLD采集SRAM数据,然后进行后续的软件处理。
2 系统误差分析及校准
星敏感器的误差来源于成像系统、软件算法两大模块。
2.1 成像系统模型及误差分析
星敏感器在采用微型化方案时,除了需要验证光电探测系统在物理器件上满足恒星探测概率阈值,还应对其模型进行分析和校准以确定探测精度。成像系统的误差来自于恒星位置、成像模型和姿态因子。
2.1.1 成像系统模型
星敏感器的姿态确定、方位导航的实现依据是:恒星较长一段时间都会静止在天球惯性坐标系中。因此本研究不考虑由于恒星位置带来的误差影响。采用公元2000年作为时间基准,图4、图5分别表示了从天球惯性坐标系和相机坐标系两个角度观测相同恒星的坐标图。
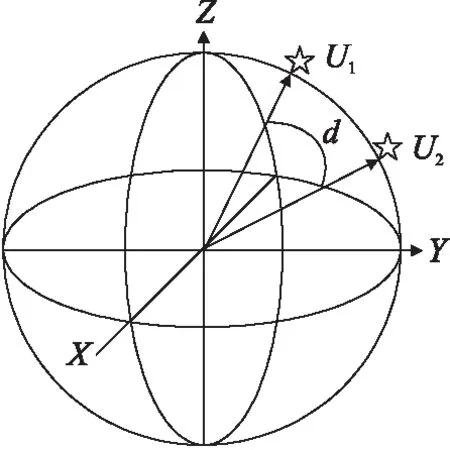
图4 天球坐标系
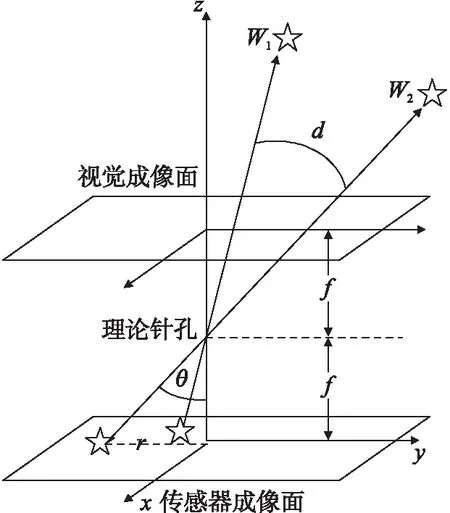
图5 像面坐标系
在不同正交坐标系中两颗星均具有相同的几何观测夹角,但带有一定的测量误差,这是星敏感器方位和姿态测量的关键精度影响因素。这种角度使用矢量内积衡量,称为恒星角距:
(1)
式中:d为角距,δ为恒星角距对应的夹角。角距是星敏感器的核心测量值,直接影响到星图识别算法和姿态解算两个关键步骤。
星敏感器并不直接测量矢量方位,而是参照模型从图像坐标点还原出天体在坐标系下的矢量。按式(1)描述,i,j两星的角距表示为dij。对于任意一颗星,其矢量由图像平面位置转换到本体矢量的方式为:
(2)
式中:(xi,yi)为恒星x、y方向测量点,(x0,y0)为相机x、y方向原点,f为归一化像方焦距(像素单位)。由于星敏感器并不直接对公式的结果进行观测,因此星敏感器必须对星敏感器相机模型参数做校准。
2.1.2 成像模型校准
为了提高星敏感器的测量精度,本文结合无维度识别算法[9]和恒星再校准方法[10],解决星敏感器的校准问题,并重新估算出相机关键的像方焦距f和图像中心位置(x0,y0)。
恒星再校准方法以f和(x0,y0)作为可变待估参量,利用恒星角距作为测量值。对于m颗样本恒星,判据使用角距测量方差:
(3)
式中:ui为星表内的恒星位置矢量,vi为样本(xi,yi)代入公式所得的观测矢量。校准过程中,通过最优估计方法改变x0、y0、f3个自变量令E达到最小。这种方法本质上融合了所有样本点的数据,通过平均加权得到需要估计的x0、y0、f3个自变量。
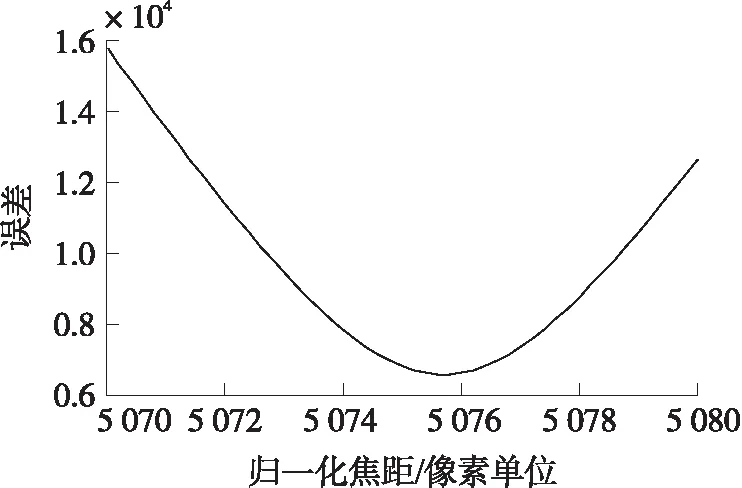
图6 f对应误差趋势
这种判据对焦距f效果显著,如图6所示,此时假设(x0,y0)无误差。然而在验证图像中心原点时效果并不突出。以图7为例,该图是恒星实测样本分析出的(x0,y0)对应的误差性能曲面,此时假定f无误差,坐标Z轴对应角距测量方差。样本所标中心点位置(x0,y0)为(459.33,659.04),归一化焦距f为5 075.7,折合原始焦距为34.0 mm。
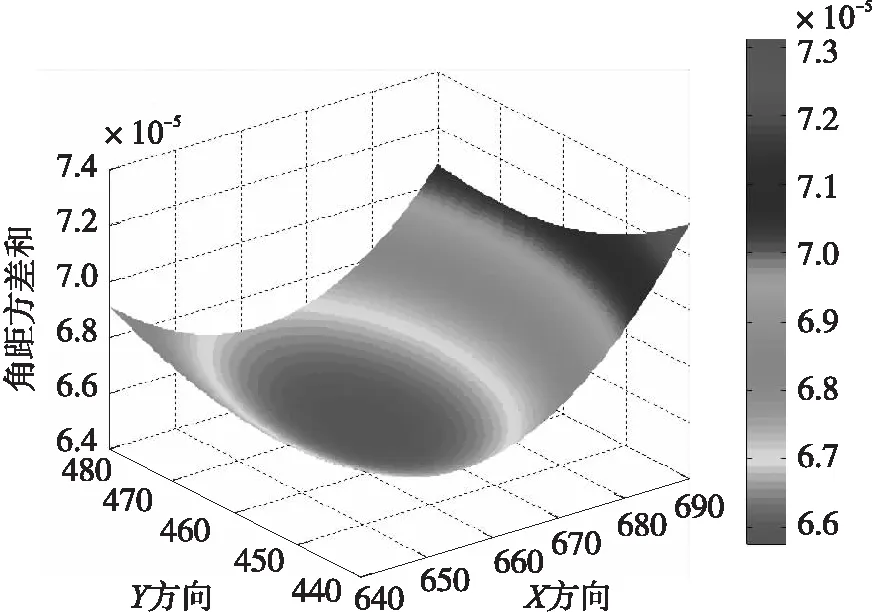
图7 (x0,y0)对应误差性能曲面
从该图可发现其领域内可收敛,但是高低梯度势差不足。首先造成恒星间角距对图像中心原点的平移并不特别敏感。此外使得最优化算法容易震荡于最低点附近。尽管如此,使用恒星校准相比地面标定仍然在测试成本、验证周期和校准真实性上具有较大的优势。
2.1.3 成像模型误差分析
视觉测量一般以点矢量作为基本的测量元素,矢量存在两个变化方向。因此星敏感器需要分析两种角度分辨精度:径向分辨率、切向分辨率。
①径向分辨率
为分析径向分辨率,令公式在平面上投影的径向偏移用另一种方法表示:
(4)
本质上公式反映了矢量与相机本体Z轴的夹角θ。假设星敏感器的定位精度以圆形范围做波动,并以偏导衡量Z轴角度θ对图像径向移动r的敏感度:
(5)
假定质心定位精度为1/10级亚像素,由公式可知。当r→0,代入归一化焦距f,径向角度敏感度约为1/f=40″每像素,则质心定位精度造成的单点矢量角度误差在4″。当像素处于图像边缘位置r→512时,则敏感度约为39″每像素。因此全画幅内敏感度无较大变化。
此外影响径向角度精度的参数还有焦距,焦距并不影响分辨率,而是直接影响了测量的模型偏差,对公式求角度θ对焦距f的变化率:
(6)
在图像边缘处焦距f如果产生1‰估计偏差,代入上一节估计的焦距参数,以及r→512,可知因为1‰焦距误差带来的角度估计误差可达20.6″。由图6可知,误差性能最低点至其2倍误差的横截距,也就是焦距容限,恰好为1‰的焦距值。
②切向分辨率
其次,星敏感器存在切向角度分辨率。对公式的平面特性做分析,其切向移动l对应切向转动角表示为:
φ/l=1/r
(7)
假定此时质心定位精度与径向时相同。当r→0,φ无法分辨因为切向移动l所造成的误差。当r→512时,质心定位造成的误差为40″;当像素处于图像角落r→820,得到最优误差25″。因此切向角度敏感度在不同的径向位置有较大变化,相对径向敏感度要低,成为星敏感器主要测量误差问题。
为了解决主要误差来源的切向角度误差,应尽量选取图像较靠近边缘的星体。然而镜头在角度较大情况下会呈现出畸变性。因此星敏感器实际选取星体时优先选取视场中圈的星体解算切向角度(Z轴姿态角度)。
2.2 星点误差分析
星敏感器中,对精度造成影响的主要软件来源是星点提取算法,但是本质上还是受到成像器的光电探测转换性能影响。星点探测的位置准确性以及可能性是星敏感器计算时的关键。该环节主要解决的是星点如何被提取为质点位置。星点的提取采用了带阈值的质心加权法,其中阈值使用如下公式:
(8)
式中:Tc为阈值用于分离背景噪声;Tv为稍小于Tc的校准值,可使像素点更多的连通域得到更大的权值,用于亮度排序。改变Tc和Tv将得到更符合实际的权重值。将公式的结果代入标准加权算法得到x,y方向的质心点:
(9)
带阈值的质心算法精度较高,可有效还原出星点位置,同时用加权综合反映出恒星亮度等级。目前普遍使用的质心加权算法一般能取得优于1/10级亚像素精度[11]。
由于星点成像领域较小,公式的阈值化环节容易被图像“盐”噪声等图像孤立点干扰,现象如图8所示。如果采用传统的星点提取和星图识别算法,将造成星点定位误差较大或者星点无法提取。

图8 中值滤波前的星点提取图像
为此,在采用现有的星点提取、星图识别和姿态算法的情况下,在星点提取环节前增加中值滤波算法而非高斯滤波,并对此展开了研究。结果显示,该方法可以滤除图像中各种孤立的奇异点对星点提取的影响,同时加强星图识别的稳定性和正确性,避免冗余的无效质点信息带来高计算负荷。下面将对此展开分析。
中值滤波采用的是领域内像素排序后取中值的方法,因此如果某个点量化灰度是孤立的,就会被直接滤除。使用3×3模板进行中值滤波迭代5次后,星点提取效果如图9所示。因此显然相比于直接使用高斯滤波,中值滤波对于图像实际可能遇见的“盐”噪声等问题得到一定程度的处理。

图9 中值滤波后的星点提取图像
虽然中值滤波在上述过程中增强了星图识别的稳定性,但是带来的代价是影响了星点的质心定位精度。为了确定中值滤波迭代过程中各项指标的变化,本文对图8中编号为SAO132444的恒星进行了分析。
图10显示了质心定位随着中值滤波迭代的实际变化过程。中值滤波在执行2次时就可消除大部分的“盐”噪声点,同时并不太大影响精度性能;迭代至6次以后所有星点几乎不再变动,这是由于中值滤波迭代最终会收敛于其根序列。从分析图可以发现,星点质心在迭代过程中不超过0.1个像素点。

图10 质心定位迭代变化趋势
姿态解算的集平均RMS如图11所示。在2次中值滤波迭代后姿态精度得到一定程度的提升;6次以后RMS基本达到收敛。
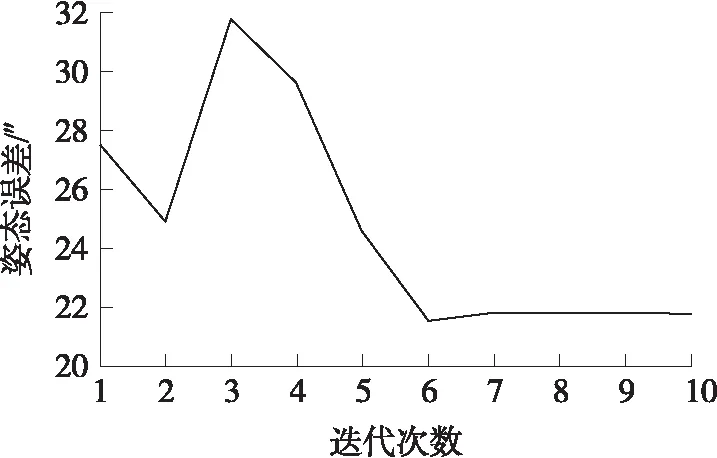
图11 姿态解算误差迭代变化趋势
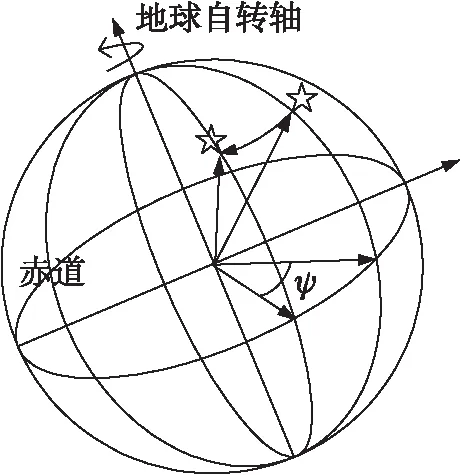
图12 基于地球自转的星跟踪
3 外场验证实验
外场实验是星敏感器精度的直接研究方式,相比较仿真星图实验,其主要目的是验证星敏感器的恒星探测和恒星识别两大研究内容。
3.1 实验设计
星敏感器的外场实验设定于北纬30°17′37.14″、东经120°9′41.12″,时间为当地时刻24时,探测目标为猎户座星群。
姿态精度确定实验方式为固定星敏感器,令其随地球自转,如图12所示。实验设计的实物图如图13所示。由于地球呈惯性旋转,且惯性章动角较小,每次采样时记录下时间标记,可获取经过时间t后的精确参考转动角ψ:
ψ=t×15 °/hour
(10)
该方法相对于地面转动实验,不仅无需考虑外部模拟转动仪器的机械精度特性[12],在转动真实性上具有真实的参考意义,可检验星敏感器对恒星的捕捉能力。同时在此实验基础上验证了恒星识别算法和姿态解算精度。

图13 实物图
3.2 恒星识别算法验证
星敏感器在未得到先验信息的情况下,恒星识别算法是其自主工作的第1步。图14展示了一张星敏感器观测图像样本,假设此时相机焦距等信息未知,使用无需相机信息的无维度算法初次识别恒星。该算法对样本图片识别后的结果信息列于表2,进而可知恒星的星表信息,按照公式确定出相机的参数信息用于后续矢量还原。
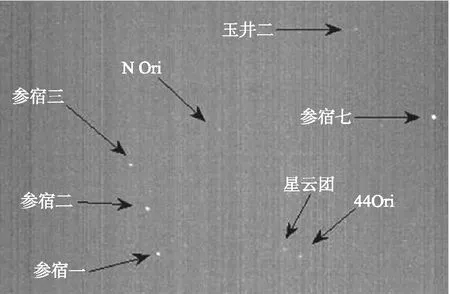
图14 星图与识别结果
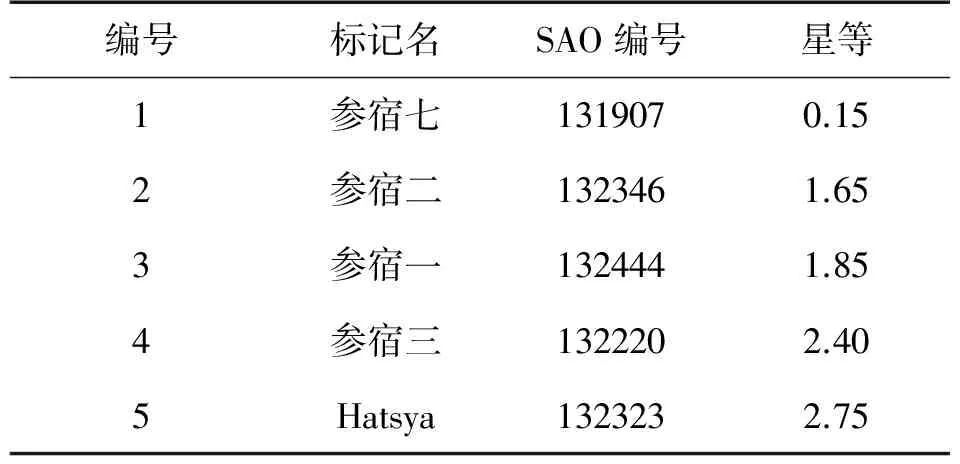
编号标记名SAO编号星等1参宿七1319070.152参宿二1323461.653参宿一1324441.854参宿三1322202.405Hatsya1323232.75
由于星敏感器实际工作时并不采用无维度识别算法而是基于角距的算法。因此首先利用上一步表2的识别信息,将恒星测量矢量与星表参考矢量代入公式,确定出模型内使用的相机参数。
星敏感器在目前两类恒星识别算法选取过程中[13],采取了基于拓扑遍历的Pyramid算法[14]。实际算法在使用第四颗星锁定基础三角形P0后,继续选取未识别星体qm与该组合的恒星逐一进行角距配对,直到识别出足够的星体才退出当次流程。该算法最理想可识别出视场内所有恒星,极大增强姿态计算的精度。为提高运算速度,算法在识别出5颗恒星时结束。星组拓扑P对星体qm扩展过程可由如下代数表示:
(11)
然后使用公式所采用的方法可成功对样本图14进行恒星识别。在识别过程中,公式对于星间匹配的关键判据是星间角距误差,此处使用如下矩阵表示:
E=arccos(WTV)
(12)
角距误差矩阵E的(i,j)元素对应了星i和星j角距对比星表计算的矢量空间误差,并列于表3,该表体现不同星间组合件的误差,如果某一颗星定位误差较大,其所在的行或列误差会普遍较大。而表内的星间角距误差在算法中足以完成匹配。

表3 星间夹角计算误差 单位:″
3.3 姿态精度验证
姿态解算是恒星识别后的最后一环步骤。为了验证姿态测量的精度,首先完成了猎户座的跟踪实验。姿态解算方面,目前广泛采用TRAID、QUEST算法,而星敏感器采用精度较高的SVD(Singular Value Decomposition)姿态解算法[15],可以简化大量的矩阵求逆运算,同时利用SVD的降维减少冗余维度的计算。
按照基于地球自转的实验方案,设当前时刻,星敏感器采集第k组样本,解算得到J2000天球系姿态矩阵Ck,初始时刻姿态矩阵为C1,则姿态转动矩阵Bk为:
(13)
由于星敏感器随地球绕轴惯性旋转,矩阵Bk其本质上即为欧拉转动角:
Φk=arccos[(traceBk-1)/2]
(14)
实验在经过一段时间的采样后,得到一系列Ф与ψ角度对比,回归与误差图如图15所示,其样本点的RMSE为30″(0.008 3°)。
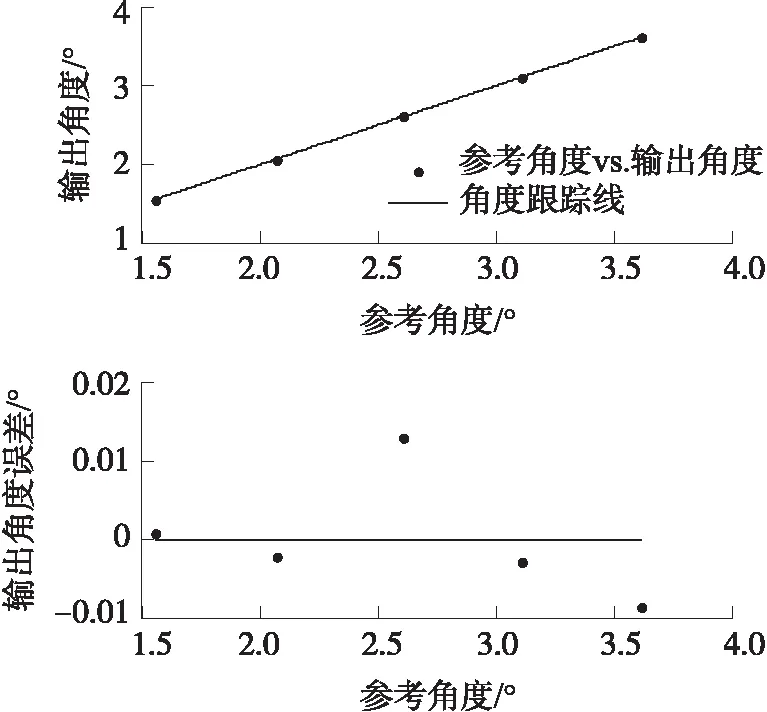
图15 星跟踪姿态测试结果
上述姿态测量误差接近于公式切向Z轴角度误差理论值。实际上,问题还来源于恒星间角距存在较大的误差,即星表未对恒星自主运动视差做更新。故星敏感器的恒星方位探测精度仍要高于该值。
4 结论及展望
星敏感器系统平台具有成像性能优秀、重量轻、体积小的优点,参数总览如表4所示。星敏感器小型化方案和关键技术得到验证,包括选择的镜头、成像器和基本算法流程。目前精度性能主要受制于星点测量精度以及星表自行处理。

表4 星敏感器参数总览
外场实验中,随地球自转的星座跟踪姿态测试表明其欧拉角回归RMSE为30″,这一精度将大幅提高微小卫星的姿态测量能力。本研究中的星敏感器将在ZDPS-3卫星上进行空间验证。
[1]Deng S,Meng T,Wang H,et al. Flexible Attitude Control Design and on-Orbit Performance of the ZDPS-2 Satellite[J]. ActaAstronautica,2016.
[2]白光耀,王昊,王志远,等. 面向微小卫星的全视场数字太阳敏感器设计[J]. 传感技术学报,2016,29(2):232-236.
[3]McBryde C R,Lightsey E G. A Star Tracker Design for CubeSats[C]//Aerospace Conference,2012 IEEE. IEEE,2012:1-14.
[4]Erlank A O,Steyn W H. Arcminute Attitude Estimation for CubeSats with a Novel Nano Star Tracker[J]. IFAC Proceedings Volumes,2014,47(3):9679-9684.
[5]梁斌,朱海龙,张涛,仝玉婵. 星敏感器技术研究现状及发展趋势[J]. 中国光学,2016(1):16-29.
[6]Bezooijen R W H V. SIRTF Autonomous Star Tracker[J]. Proceedings of SPIE—The International Society for Optical Engineering,2003,4850:108-121.
[7]Blarre L,Ouaknine J,Oddosmarcel L,et al. High Accuracy Sodern Star Trackers:Recent Improvements Proposed on SED36 and HYDRA Star Trackers[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit. 2006.
[8]王萌萌. 适用于皮纳卫星的微型星敏感器设计与测试[D]. 浙江大学,2014.
[9]Samaan M A,Mortari D,Junkins J L. Nondimensional Star Identification for Uncalibrated Star Cameras[J]. The Journal of the Astronautical Sciences,2006,54(1):95-111.
[10]Enright J,Jovanovic I,Vaz B. On-Orbit Star Tracker Recalibration:A Case Study[C]//Aerospace Conference. IEEE,2015:1-13.
[11]李春艳,谢华,李怀锋,等. 高精度星敏感器星点光斑质心算法[J]. 光电工程,2006,33(2):41-44.
[12]Wei X,Zhang G,Fan Q,et al. Star Sensor Calibration Based on Integrated Modelling with Intrinsic and Extrinsic Parameters[J]. Measurement,2014,55(9):117-125.
[13]Spratling B B,Mortari D. A Survey on Star Identification Algorithms[J]. Algorithms,2009,2(1):93-107.
[14]Mortari D,Samaan M A,Bruccoleri C,et al. The Pyramid Star Identification Technique[J]. Navigation,2004,51(3):171-183.
[15]Yin H,Song X,Yan Y. Robustness ANALYSis and Improvement of Singular Value Decomposition Algorithm for Autonomous Star Identification[J]. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering,2015,229(10):1757-1770.

李 赓(1991-),男,浙江大学微小卫星研究中心,硕士研究生,研究方向为卫星姿态确定与控制系统,lgzju@zju.edu.cn;

王 昊(1974-),男,浙江大学微小卫星研究中心,副教授,研究方向为卫星姿态控制、MEMS惯性器件、信号处理,roger@zju.edu.cn。
Research on StarTracker for Micro-Satellites*
LIGeng,WANGHao*,JINZhonghe,WANGBendong
(School of Aeronautics and Astronautics,Zhejiang University,Hangzhou 310027,China)
A new design of star tracker(ST)is proposed. The STisbased on the using of commercial devices,to matchMicro-satellites’ compact size. The STconsists of an industrial lens,a DSP processor,a low power CPLD and a grayscale CMOS sensor. To improve the measurement accuracy,theimaging model of the STis analyzed,andthe optical parameters are compensated by in-field star calibration. The algorithm of star photoprocessing is also analyzed,anda median filter is applied to reduce the effect ofimpulse noise during star point extracting. A ST prototype is tested with field experimentsbased on the earth’s rotation and constellation tracking,the results show that the prototype’s RMSE(Root Mean Square Error)of Euler angleis 30″. The prototype,whichis in compact size and low power consumption,can be exactly applied to Micro-satellites.
star tracker;micro-satellite;attitude determination
项目来源:国家杰出青年基金项目(61525403)
2016-12-30 修改日期:2017-04-07
V448.222
A
1004-1699(2017)08-1145-07
C:7630
10.3969/j.issn.1004-1699.2017.08.002
