基于粗糙集和聚类方法的装配间隙优化模型

王正祥，常文兵，苑星龙，钱思霖

(1.河南柴油机重工有限责任公司，河南 洛阳471000；2.北京航空航天大学可靠性与系统工程学院，北京 100000)

基于粗糙集和聚类方法的装配间隙优化模型

王正祥1，常文兵2，苑星龙2，钱思霖2

(1.河南柴油机重工有限责任公司，河南 洛阳471000；2.北京航空航天大学可靠性与系统工程学院，北京 100000)

本文提出了柴油机装配间隙参数与柴油机质量水平定量关系的优化模型。柴油机的装配过程是影响产品质量的重要因素，装配间隙参数是柴油机装配过程的重要表征参数。研究引入粗糙集和k-均值聚类算法建立分析模型。数据源是某柴油机的装配间隙参数。本文建立了柴油机装配间隙参数与质量水平近似依赖关系的决策系统。以16缸装配间隙参数数据和质量级数据为例，验证了所提模型的正确性。实证结果表明，该模型在现实中可行。

装配间隙；粗糙集；聚类算法；优化模型

柴油机是船舶动力的核心，在柴油机的生产过程中，装配过程是影响柴油机长期质量的重要环节，其装配间隙参数是影响柴油机装配质量的重要因素。目前，还没有应用数据挖掘方法的定量相关程度的研究。

冯晓芳等[1]以梁柱组合产生的装配间隙为研究对象，分析了装配间隙对该结构性能在整个装配过程中的影响，并对多种装配间隙取值下的结构性能进行有限元仿真分析，得出装配间隙参数取值和梁柱结构性能的关系。唐亮等[2]针对具体研究对象装配过程中的间隙状况提出了4种面向装配间隙的模型。熊小龙等[3]应用Topsis方法，为柴油机装配质量的评估提供了定量分析的方法，并通过算例实验验证该评价方法的有效性和可行性。

经典粗糙集是由波兰数学家Z.Pawlak最先提出的，粗糙集的最初定位是一种处理不完整和不确定性知识的数学工具。Roman和Daniel于1995年提出了基于相似关系的粗糙集。Dubois和Prade提出了模糊粗糙集的概念，这是在粗糙集理论方面的一个重要推广。K-means算法是一种应用最为广泛的基于划分的聚类算法，Teng Li等提出了一种多内核的K-means聚类算法，Marco Capo等针对大量数据问题提出了一种有效的近似K-means聚类算法。

本文旨在通过建立基于粗糙集和k-均值聚类算法的决策系统，挖掘装配间隙参数与柴油机质量水平之间的关系。

1 基础理论

1.1 经典粗糙集理论

粗糙集的相关理论是建立在一个信息系统IS=(I,A)之上的，其中，I为论域，A为属性集，I和A均为非空有限集合。

当信息系统满足条件：A=C∪D和C∪D≠∅时，称这样的信息系统为决策系统：DS=(I,C∪D)，其中，C为条件属性集，D为决策属性集。

定义1：不可分辨关系。对于一个信息系统IS=(I,A)，B⊆A是属性集合的一个子集，称二元关系IND(B)={(x,y)∈I×I∶∀a∈B,a(x)=a(y)}为信息系统IS的不可分辨关系，记作IND(B)。其中，x和y为论域I中的元素，a为属性子集中的任一属性，a(x)代表该元素在属性a上的取值。

定义2：等价类。对于一个信息系统IS=(I,A)，B⊆A是属性集合的一个子集，不可分辨关系IND(B)将论域I划分为若干个等价类。I/IND(B)表示所有等价类的集合，[x]IND(B)表示包含元素x的等价类。

定义3：上近似和下近似。对于信息系统IS=(I,A)，B⊆A是属性集合的一个子集，X⊆I是论域的一个子集，

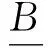
(1)

分别为X的B-下近似和X的B-上近似。

定义4：精确度和隶属度。粗糙集X的精确度和隶属度分别表示为：

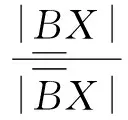
(2)

定义5：隶属函数。

(3)

隶属函数表示了元素x对粗糙集X的隶属情况。

定义6：决策系统的精度。

(4)

定义7：带可变精度粗糙集的上下近似集。对于信息系统IS=(I,A)，B⊆A是属性集合的一个子集，X⊆I是论域的一个子集，0.5≤β≤1为精度变量，

(5)

分别为X在精度变量β下的B-下近似和B-上近似。

1.2 K-means聚类算法

K-means聚类算法使用欧式距离，通过最小化目标函数J最小化在同一个聚类中的样本之间的距离，并最大化在不同聚类中样本的距离。

(6)

其中n是数据集中数据点的个数(即样本个数)，xik代表数据点各维度下的参数值，zik为隶属函数，vi是聚类中心。

K-means聚类算法中的隶属函数用如下公式来表示：

聚类中心vi可通过如下公式计算得到：

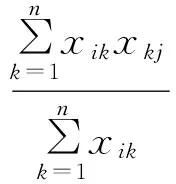
(7)

K-means聚类算法的实现步骤是：a.选择初始的聚类个数k；b.随机选择初始聚类中心vi；c.将各个数据点xij分配到与其距离最近的聚类中；d.根据聚类中心vi的计算公式重新计算聚类中心；e.重复步骤(c)和步骤(d)，直到目标函数J的值不再发生变化。

2 数据源与数据预处理

2.1 数据源

本文数据来源是某型号柴油机的装配间隙参数和质量等级数据。实证研究的数据集是从16缸柴油发动机的初始数据集，包括29个样本。装配间隙参数来自四个对柴油机整机质量等级影响程度较大的部件，编号分别为2K，5K，10K，11k。

2.2 数据预处理

在对初始数据集进行分析后，在编号2K的组件中存在缺失值，选择多重插补处理缺失值，生成完整的数据集。完成实证数据的相关性分析后，可以得出各种部件的装配间隙参数之间的相关性很弱，但同一部件的装配间隙参数之间的相关性很强。因此，可以用主成分分析法来降低数据集的维度。完成数据预处理后，初始数据集的56个装配间隙参数降维成为15个部分，这15个部分可以代替初始数据集的所有装配间隙参数，并保留初始数据集的大部分信息。最后，实证研究的数据集的装配间隙参数和柴油机的质量水平需要综合得到最终的数据集，直接用于后续的数据挖掘。

3 基于粗糙集和K-means聚类算法的优化模型

3.1 条件属性集和决策属性集对论域的划分

在完成对原始数据集预处理的基础上，用经过数据预处理的新数据集代替原始数据集，在新的数据集的基础上依据这15个成分，使用K-means聚类算法对属性集中的样本进行聚类，完成条件属性集对论域的划分。聚类个数选择过程：在工程实践中需要在预设的聚类个数范围内选择使聚类效果达到最优的K-means的中心点的个数，在K-means聚类中，聚类效果用聚类优度这一指标来衡量。

在本实证研究案例中，结合研究对象和决策属性集对论域进行划分的结果，设置初始的聚类个数范围为3～15个。在该初始聚类范围下分别建立K-means聚类模型，输出其聚类优度的结果并绘制聚类个数与聚类优度的关系图，如图1所示。

由图1可以看出，在给定的初始聚类个数范围下，当聚类个数为7时，其聚类优度，即组间平方和同总平方和的比值就可以达到0.86，故在实证研究案例中，选择7作为依据K-means聚类算法完成柴油机装配间隙参数对柴油机样本聚类过程的聚类个数。

在完成条件属性集对实证研究数据集样本空间划分的基础上，条件属性集和决策属性集对16缸柴油机样本的划分结果如表1所示。

图1 聚类个数与聚类优度关系图Fig.1 Cluster number and clustering excellence relationship diagram

编号结果质量等级编号结果质量等级编号结果质量等级编号结果质量等级编号结果质量等级11合格品76合格品132一等品195一等品257一等品21合格品86一等品142一等品205一等品267合格品31一等品94合格品152合格品215一等品277优等品41合格品104一等品162优等品225优等品287优等品56优等品114一等品172优等品235一等品297优等品66一等品124一等品183一等品245合格品

决策属性集包含柴油机的整机质量等级，整机质量等级为分类型的属性，所以直接依据粗糙集中等价类的概念就可以完成决策属性集对等价类的划分，将实证研究中的16缸柴油机样本划分为优等品、一等品和合格品3个质量等级，即：U/D={X1,X2,X3}是依据决策属性集将论域划分为的3个等价类。

X1={5,16,17,22,27,28,29}

X2={3,6,8,10,11,12,13,14,18,19,20,21,23,25}

X3={1,2,3,7,9,15,24,26}

其中，数字编号代表柴油机编号，X1是由整机质量等级为优等品的柴油机样本组成的集合，X2是由整机质量等级为一等品的柴油机样本组成的集合，X3是由整机质量等级为合格品的柴油机样本组成的集合。

条件属性集中包含经过柴油机装配间隙参数经降维处理后的15个成分，由于其为数值型的属性，故选择K-means聚类算法完成条件属性集对论域的划分，可以将论域划分为7个近似等价类：

U/C={E1,E2,E3,E4,E5,E6,E7}，E1={1,2,3,4}，E2={13,14,15,16,17}，E3={18}，E4={9,10,11,12}，E5={19,20,21,22,23,24}，E6={5,6,7,8},E7={25,26,27,28,29}。

其中，数字编号代表柴油机的编号，E1～E7代表依据条件属性集对论域进行划分后的7个近似等价类。

3.2 柴油机装配间隙和整机质量等级之间的决策系统

至此建立了柴油机装配间隙和整机质量等级之间的决策系统，该决策系统中包含如下决策规则：

E7→X1，E3→X2，E4→X2，E5→X2，E1→X3

决策规则代表柴油机装配间隙参数所属的近似等价类以及由该装配间隙组合所决定的整机质量等级。从条件属性集对论域聚类划分的角度来讲，当柴油机装配间隙参数组合落在E7这个聚类中时，可认定其整机质量等级为优等品；当柴油机装配间隙参数组合落在E3,E4,E5中的某一个聚类中时，可认定其整机质量等级为一等品；当柴油机装配间隙参数组合落在E1这个聚类中时，可认定其整机质量等级为合格品。

3.3 决策系统的精度评价

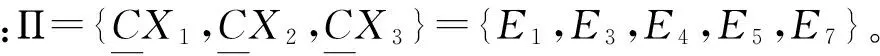
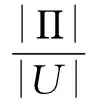
因此，该决策系统的条件属性集和决策属性集之间存在部分依赖关系：

{柴油机装配间隙参数}→0.68{柴油机整机质量等级}

λ的取值代表该部分依赖关系的程度，即柴油机整机质量等级在多大程度上取决于柴油机的装配间隙参数。

4 结语

发动机的装配过程是影响发动机质量的关键因素，其装配间隙参数是影响柴油机装配质量的重要因素。本文以某厂某型号发动机装配间隙参数和整机质量等级为原始数据集，利用粗糙集理论和K-means聚类算法，建立了装配间隙参数与整机质量等级之间的决策系统，实现了装配间隙参数组合的优选。最后，通过实证研究证明了该方法的可行性和有效性，对柴油机的生产装配过程有一定的指导意义。

[1] 冯晓芳，吕志军，杨建国，等. 梁柱组合装配间隙及其对钢货架性能的影响分析[J].东华大学学报(自然科学版)，2012，38(05):524-528.

[2] 唐亮，王建梅，陶德峰，等. 装配间隙对风电锁紧盘性能的影响分析[J].太原科技大学学报，2013，34(02):125-129.

[3] 熊小龙，王建国，冯洲鹏. 柴油机装配质量评估的TOPSIS方法[J].柴油机，2014，(03):22-24.

Assembly clearance optimization model based on rough set and clustering method

WANG Zheng-xiang1, CHANG Wen-bing2, YUAN Xing-long2, QIAN Si-lin2

(1. Henan Diesel Heavy Industries Co., Ltd., Luoyang 471000, China; 2.School of Reliability and System Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100000, China)

This paper presents an optimization model for the quantitative relationship between diesel engine assembly clearance parameters and diesel engine quality level. The assembly process of the diesel engine is an important factor affecting the quality of the product. The assembly gap parameter is an important characterization parameter of the diesel engine assembly process. The data source is the assembly gap parameter of a diesel engine. In this paper, a decision system of diesel engine assembly gap parameter and quality level is established. The correctness of the proposed model is verified by taking the 16th cylinder assembly gap parameter data and the quality level data as an example. The empirical results show that the model is feasible in reality.

Assembling clearance; Rough set; Clustering algorithm; Optimization model

2017-03-11

TP391.72

A

1674-8646(2017)14-0177-04