电动直线加载系统多闭环复合控制

徐志伟，范元勋

(南京理工大学 机械工程学院，南京 210094)

电动直线加载系统多闭环复合控制

徐志伟，范元勋

(南京理工大学 机械工程学院，南京 210094)

为实现对某型航天用直线运动伺服系统的半物理实物加载测试，设计了一种模拟其实际受载的电动直线加载系统。针对电动直线加载系统多余力矩强扰动及其他非线性因素影响力矩跟踪精度的问题，提出一种引入前馈补偿，以力矩闭环作为外环、转速闭环为内环的多闭环复合控制策略，并在力矩外环采用模糊自适应PID控制器。给定阶跃信号和正弦载荷进行直线加载跟踪性能对比仿真分析，结果表明在不同频率下有效满足跟踪性能要求；在不同扰动频率和幅值情况下进行多余力矩抑制对比仿真分析，与传统闭环相比，多闭环复合控制策略有效地抑制了加载系统的多余力矩，提高了直线加载跟踪精度和系统动态响应性能。

电动直线加载系统；模糊自适应PID；多闭环复合控制；多余力矩抑制

0 引言

随着国防建设的需要和航空航天技术的不断发展，某型直线运动伺服驱动系统得到广泛的应用。电动直线加载系统(Electric Linear Loading System,ELLS)能够于实验室条件下根据直线运动伺服机构的实际受载状况对其进行模拟加载，将传统的自破坏性全实物试验转变成实验室条件下的半实物仿真试验，以考核其在实际工况下的工作性能及可靠性[1]。电动直线加载作为典型非线性的被动式加载，直线运动伺服系统主动运动引起的多余力矩影响电动直线加载系统(ELLS)的控制精度、频宽及稳定性，故如何尽可能地抑制乃至消除多余力矩干扰是电动直线加载系统(ELLS)的关键问题[2]。

目前，国内外学者主要从结构补偿和控制策略优化上对多余力矩抑制进行了研究。文献[3]在结构上引入了弹簧杆作为连接缓冲机构，并采用舵机角速度作为前馈补偿，加载试验数据表明能够满足“双十指标”，但针对不同负载的加载梯度须更换弹簧杆，不能满足自动加载的要求；文献[4]基于结构不变性原理引入舵机速度和位置前馈来抑制多余力矩，其缺点在于系统需建立精确的逆模型；文献[5]提出基于非均匀量化思想的改进小脑模型(CMAC)，但小脑模型网络结构设计缺乏相应的理论指导，较难推广应用；文献[6]应用迭代学习控制整定PID参数，所构成复合控制器存在计算量大、给定值修正频繁的问题。

针对ELLS多余力矩影响控制精度、加载频宽及稳定性问题，基于闭环控制与串联控制的优点，对ELLS进行性能分析后，本文设计一种基于前馈补偿控制、串入力矩外环控制和速度内环控制的控制方法，并在力矩外环引入模糊自适应PID控制器[7]，与传统的闭环控制进行了理论分析与比较，对比仿真验证了其有效性。

1 ELLS结构和数学模型

1.1 ELLS结构

ELLS的系统结构如图1所示。ELLS测试系统主要由加载电机(直流力矩电机)、波纹管联轴器、转矩转速传感器、滚珠丝杆副、光栅尺、拉压力传感器及被加载直线运动伺服系统组成。直流力矩电机具有高刚度、高线性、小扭矩波动及能长时间处于堵转状态等优点，故采用直流力矩电机作为ELLS的驱动元件。采用高精度、无侧隙的大导程滚珠丝杆副将伺服加载电机的扭矩输出变为直线加载。拉压力传感器用来实时测量ELLS加载力的大小，并经AD转换反馈给工控机。

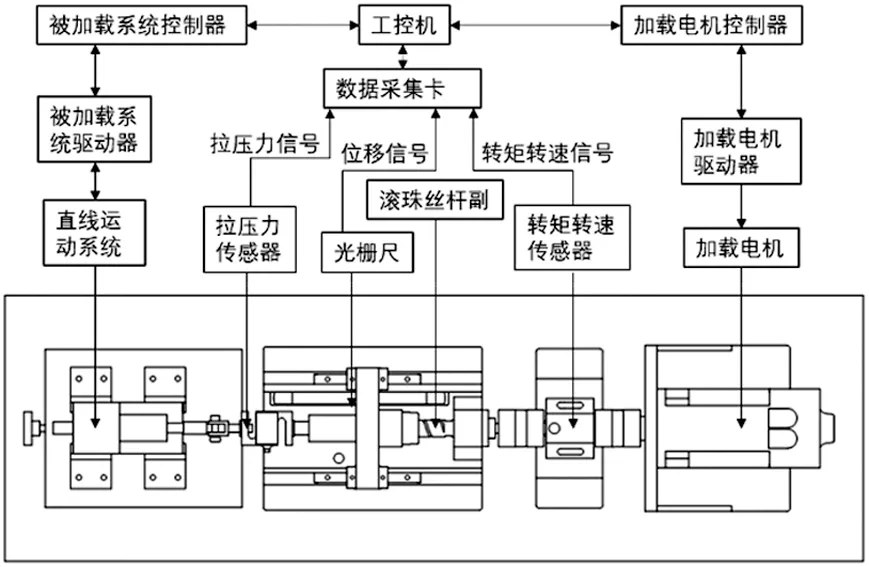
图1 ELLS结构

由图1可知，ELLS与直线运动伺服机构通过连接轴刚性连接，当ELLS参考输入指令信号为零时，由直线运动机构作主动直线运动所引起ELLS的输出力矩即为多余力矩。

1.2 ELLS数学模型

直流力矩伺服电机可等效为一电感元件和一线性电阻串联而成，由电压平衡方程和转矩平衡方程可得直流力矩电机传递函数：

(1)

式中:TL为电机输出转矩；Kt为电机电磁转矩系数；Um为电枢绕组的端电压；Ke为电机反电动势常数；Jm为电机转动惯量；Bm为电机阻尼系数；Lm为电枢回路总等效电感；Rm为电枢回路总电阻；θm为力矩电机的角位移。

ELLS采用脉宽调制(PWM)驱动装置，由于大功率晶体管的开关频率远大于加载电机的工作频率，PWM输出信号中的交流分量影响很小，实际起作用的是直流分量，因此PWM驱动装置可视为比例环节，其数学模型为：

(2)

式中:KPWM为PWM驱动装置等效增益；Ui为控制电压信号。

ELLS将伺服加载电机的扭矩输出变为直线加载需经波纹管联轴器、转矩转速传感器、滚珠丝杆副等元件转换，而这些元件的刚度对ELLS的加载性能有着一定影响。将中间转换元件和被加载直线运动机构按系统负载考虑，且负载与电机刚性连接，因此电机输出转矩包括模拟惯性负载、阻尼负载及弹性负载，建立其平衡方程为[8]:

(3)

式中:JL为负载等效转动惯量；BL为负载阻尼系数；KL为负载等效弹性刚度系数；θL为负载角位移。

ELLS采用高精度、无侧隙的滚珠丝杆副将伺服加载电机的扭矩输出变为直线加载，根据滚珠丝杠副受力模型，可得电机输出转矩与直线加载力关系、负载角位移与直线加载位移关系为[9]：

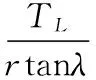
(4)

式中:F为直线加载力；r为丝杠半径；λ为滚珠丝杠副螺纹升角；L为直线加载位移;P为滚珠丝杠副导程。

综合式(1)～式(4)可得ELLS整体数学模型，其传递函数为：

F=G3Ui-G4L

(5)

其中：

(6)

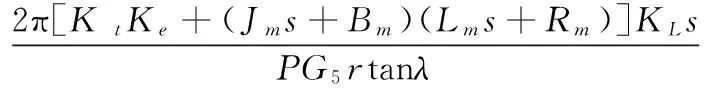
(7)

G5=(Lms+Rm)[(Jm+Bm)s2+(Bm+BL)s+KL]+KtKes

(8)

由式(5)可知，ELLS直线加载力输出受给定电压信号Ui和直线运动伺服系统输出直线位移L的共同影响。令L=0，即直线运动伺服系统不输出位移，则有：

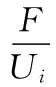
(9)

式(9)表示ELLS不受被加载直线运动伺服系统扰动情况下的前向通道特性。式(5)中令Ui=0，则有：

(10)

式(10)表示ELLS的扰动通道特性，且负号的物理含义表示扰动加载力的方向与被加载直线运动伺服系统的位移方向相反。

ELLS整体数学模型控制方框图如图2所示。图2中，ωm为电机转动角速度；Em为电枢反电动势；im为电枢电流；Tm为电机电磁转矩。

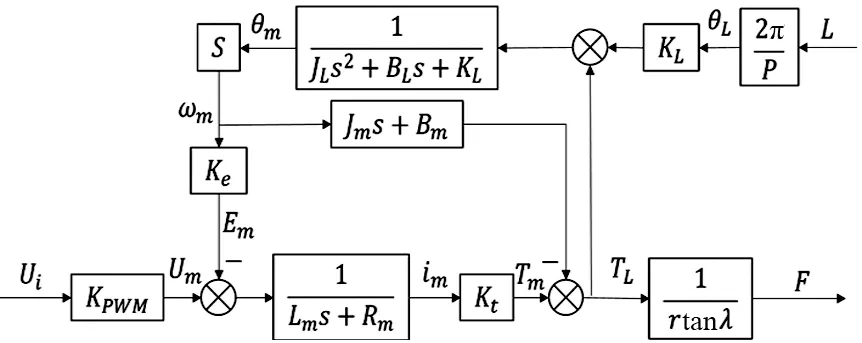
图2 ELLS整体数学模型控制方框图

2 ELLS性能分析与控制器设计

2.1 ELLS性能分析

在对ELLS系统控制器设计及调试之前，为验证其稳定性，须先对其进行性能分析[10]。ELLS系统参数表如表1所示。

表1 系统参数表

ELLS可近似被视为惯性加载系统，故负载阻尼系数BL可近似为零。结合ELLS数学模型，当加载系统作主动运动时，直线运动伺服系统输出位移L为零，若设定参考值KPWM=1，得ELLS开环传递函数并代入表1参数，即：

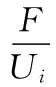
(11)

利用MATLAB编程求得式(11)伯德图，可知ELLS幅值裕度Kg=-77dB，相位裕度γ=-88.4°，由伯德图的物理意义可知系统不稳定。但可调节剪切频率ωc滞后于当前剪切频率，使相频特性距-180°的相位差γ>0°，从而使相位裕度和幅值裕度满足稳定条件。依据滞后校正原理，在式(11)上串联滞后校正，求得其传递函数为：

(12)

滞后校正后开环系统的相位裕度γ=90.4°>0°，幅值裕度Kg>0dB，采用乃奎斯特稳定性判定系统稳定。

2.2 ELLS前馈补偿控制器设计

针对ELLS外部扰动，利用前馈控制补偿法中按干扰补偿的方法进行多余力矩补偿设计。因负载等效弹性刚度系数KL很大，可近似视为被加载直线运动伺服系统的转速ωL与加载电机转速ωm相等。由图3可知补偿控制器Gn(s)须由两部分Gn1(s)与Gn2(s)组成，Gn1(s)补偿反电动势引起的多余力矩，Gn2(s)补偿由惯性引起的多余力矩。基于前馈控制补偿条件，Gn1(s)、Gn2(s)需满足：

(14)

由式(13)、式(14)可得前馈补偿控制器Gn(s)，并代入表1参数得：

sGn(s)=5.928×10-6s3+1.092×10-3s2+1.872s

(15)

式中，三项分别补偿了由加速度变化率、加速度及速度所引起的多余力矩。可直接测得被加载对象的位置及速度信号，加速度信号及其变化率则要以微分环节来实现，但在高频信号下易导致微分环节振荡，可考虑只引入速度前馈补偿。

2.3 ELLS外环控制器设计

基于力/力矩闭环的外环控制器，其目标为抑制ELLS的外部干扰、加快其动态频率响应及提高力跟踪精度。实验调节发现，常规PID控制难以实现对非线性和时变环节的精确加载，例如积分饱和环节及加载启动阶段，加载系统控制性能明显下降，乃至出现畸变[11]。外环控制器Gd采用模糊自适应PID控制，由常规PID控制器和模糊推理参数校正部分组成。

选取系统误差e及误差变化率ec为控制器输入语言变量，选取△KP、△Ki、Kd输出语言变量，输入输出模糊子集均定义为{NB,NM,NS,ZO,PS,PM,PB}，划定论域[-6,6]，变量分布均服从三角分布，模糊推理应用MAX-MIN规则，解模糊应用重心法，模糊规则见文献[12]。实时查表并代入式(16)求得合理参数。

(16)

加入前馈补偿控制器和外环控制器的ELLS多闭环复合控制结构框图如图3所示。

图3 ELLS多闭环复合控制结构框图

3 仿真结果分析

为验证ELLS多闭环复合控制的有效性，利用MATLAB/Simulink对其进行对比仿真分析，以验证多余力/力矩抑制效果和直线加载性能。仿验中，外环控制器Gd采用模糊自适应PID控制，量化因子为3.6、0.2，比例因子为0.1、2和0.033。

3.1 直线加载跟踪性能仿真

给定加载力为3000 N的阶跃控制信号，被加载直线运动伺服系统输入信号为幅值1 mm、频率2 Hz和5 Hz的正弦信号，仿真时间取5 s，跟踪曲线如图4所示。

由图4可知，当扰动频率为2 Hz时，ELLS对阶跃响应跟踪效果较好，跟踪误差小于50 N，为输入加载力的1.67%；当扰动频率增大至5 Hz时，跟踪误差明显增大至260 N，为输入加载力的8.67%。可见ELLS在阶跃响应时的超调量和响应时间满足ELLS动态跟踪性能的要求。

(a)干扰信号为1 mm/2 Hz时的阶跃跟踪曲线

(b)干扰信号为1 mm/5 Hz时的阶跃跟踪曲线图4 ELLS阶跃信号跟踪曲线

工程实际中常用加载指令力矩与实际输出力矩间的相位差与幅值差来衡量一个加载系统的动态跟踪性能，当幅值误差小于±10%和相位误差变化小于10°即为“双十指标”[13]。直线运动伺服系统以幅值为1 mm、频率与加载力相同做正弦运动，作出加载力幅值为3000 N，频率分别为2 Hz、5 Hz和10 Hz时的ELLS加载力正弦跟踪曲线。为验证ELLS多闭环复合控制的有效性，给出相同加载条件下单闭环控制和复合控制的正弦跟踪曲线，进行对比分析。图5仅给出加载频率为2 Hz时的对比曲线。

(a)干扰信号为1 mm/2 Hz时的单闭环控制跟踪曲线

(b)干扰信号为1 mm/2 Hz时的复合控制跟踪曲线图5 ELLS输出力正弦跟踪曲线

图5a和图5b分别是当加载频率为2 Hz时ELLS单闭环控制和复合控制下的跟踪效果，在被加载系统以幅值1 mm及频率2 Hz的正弦扰动下，单闭环控制较复合控制明显幅值超调大，相位滞后明显，输出加载力跟踪幅值误差已大于10%，远远达不到“双十指标”；图5b为复合控制下加载力跟踪曲线，输出力与输入力曲线基本重合，幅值误差和相位滞后小，ELLS跟踪性能大大改善。当加载频率提高至5 Hz及10Hz时，跟踪效果较好，输出力曲线幅值误差和相位滞后较小，加载精度满足理想的“双十指标”。

3.2 多余力/力矩抑制仿真

抑制多余力/力矩的能力是衡量伺服加载系统加载能力的一重要指标。为测量ELLS多余力矩，令输入指令加载力为0 N，被加载直线运动机构分别运行于2 Hz、5 Hz及10 Hz三种频率条件下，幅值为1 mm、2mm及5mm。仅给出1 mm/2 Hz时的多余力矩曲线，完整多余力矩抑制结果见表2。

图6 信号为1 mm/2 Hz时的复合控制多余力矩曲线

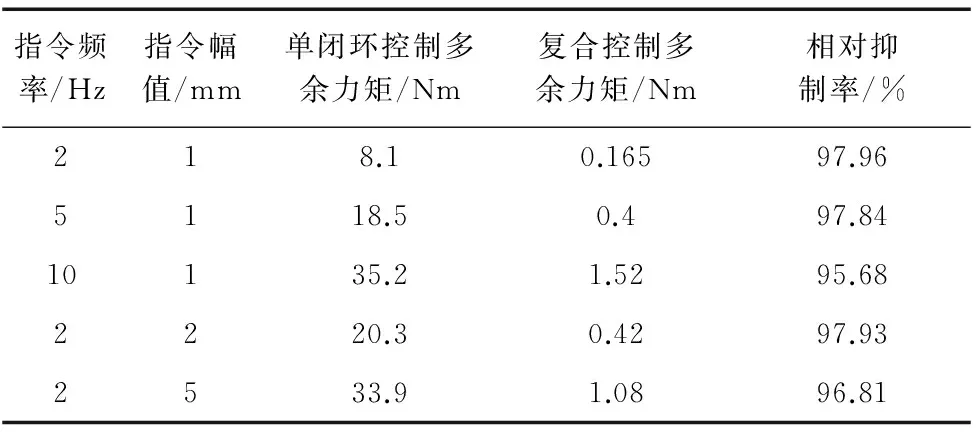
表2 ELLS多余力矩抑制

相较于扰动信号幅值的影响，多余力矩相对抑制率受扰动频率的影响更大，这是由于受载机构是以影响电枢电流而产生多余力矩的，且其具有微分特性；前馈补偿控制器Gn(s)的加速度及其变化率补偿部分以微分环节来实现，但在高频信号下易导致微分环节振荡；且ELLS扭矩输出转化为直线力过程中有较大增益。故多闭环复合控制多余力矩抑制效果在中低频扰动下较为明显，相对抑制率达到95%以上，满足了ELLS指标要求。

4 结论

针对航天用某型直线运动伺服系统，设计了测试其承载性能的电动直线加载系统(ELLS)；针对 ELLS的特点及传统单闭环控制存在的缺点，对ELLS进行性能分析后，基于传统闭环控制，设计了增加前馈补偿、转速内环及力矩外环的多闭环复合控制方法，并在力矩外环引入了模糊PID控制器。经仿真实验表明，多闭环复合控制策略能够在不同扰动频率的情况下实现较高的力矩加载精度，在不同扰动频率和幅值的情况下有效地抑制了多余力矩，保证了ELLS力矩跟踪精度和动态性能，并且该方法结构简单，易于工程实现，对电动直线加载系统的设计有着较大的参考价值。

[1] 齐蓉,林辉,陈明.被动式电动加载系统多余力的研究[J].控制与决策,2006,21(2):225-228.

[2] Wang Zhe,Wang Minyan,Wang Guoqiang.Simulation analysis of a new electric dynamic load simulator based on duoblestator permanent-magned synchronous motor[C]//Power Electr-onics and Motion Control Conference, June 2-5, 2012, Harbin, China. 2012: 2617-2620.

[3] 王鑫,冯冬竹.引入弹簧杆的电动负载模拟器实验研究[J].电机与控制学报,2012,16(9):91-94.

[4] 李成功,靳红涛,焦宗夏.电动负载模拟器多余力矩产生机理及抑制[J].北京航空航天大学学报,2006,32(2):204-208.

[5] 杨波,王哲.新型小脑模型关联控制器复合控制在电动加载系统中的结构及算法[J].控制理论与应用,2011,28(6):827-833.

[6] 王明彦,郭奔.基于迭代学习控制的电动伺服负载模拟器[J].中国电机工程学报,2003,23(12):123-126.

[7] 汤红诚,李著信,王正涛,等.一种模糊PID控制系统[J].电机与控制学报,2005,9(2):136-138.

[8] Sebastian Abu.Design methodologies fot robust neon positioning[J].IEEE Transactions on Control Systems Technology, 2005,13(6):868-876.

[9] 濮建荣.行星滚柱丝杠副接触、摩擦与工作特性的理论与试验研究[D].南京:南京理工大学,2015.

[10] 葛邵鹏程,范元勋.直线运动机构电动加载测试系统建模及仿真分析[J].组合机床与自动化加工技术,2016(9):91-94.

[11] 吕帅帅,林辉.电动加载系统分数迭代学习复合控制[J].北京航空航天大学学报,2016,42(9):1944-1951.

[12] 吕帅帅,林辉,樊明迪.电动加载系统多闭环复合控制[J].电机与控制学报,2015,19(9):16-21.

[13] 焦宗夏,华清,王晓东.负载模拟器的评价指标体系[J].机械工程学报,2002,38(11):26-30.

(编辑 李秀敏)

Electric Linear Loading System with Multi Closed-up Compound Control

XU Zhi-wei, FAN Yuan-xun

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

To realize the handware-in-the-loop loading test of a certain type of linear motion servo system in space application, an electic linear loading system is designed for simulating the actual working condition of the linear motion servo system. To solve the problem that the disturbance of surplus torque and the nonlinearity deteriorate the precision of torque tracking in the electric linear loading system, a multi closed-loop control strategy with closed-loop torque as outer loop, closed-loop speed as the inner loop and feed-forward compensation is proposed. And the closed-loop torque adopts fuzzy adaptive PID algorithm. The step signal and sine load singal is given and the linear load tracking performance is contrastively simulated and analyzed. The results show that the proposed method effectively meets the tracking performance requirments. The simulation of surplus torque inhibition is contrastively analyzed under the condition of different disturbance frequency and amplitude. Compared with traditional closed-loop, the proposed method effectively suppresses the disturbance of surplus torque, improves the tracking precision and dynamic performance of electric linear loading system.

electric linear loading system; fuzzy adaptive PID; multi closed-loop compound control; surplus torque suppression

1001-2265(2017)08-0089-04

10.13462/j.cnki.mmtamt.2017.08.022

2016-11-13；

2017-01-03

徐志伟(1992—)，男，山东潍坊人，南京理工大学硕士研究生，研究方向为伺服加载测试系统，(E-mail)115101000006@njust.edu.cn；通讯作者：范元勋(1964—)，男，江苏南通人，南京理工大学教授，硕士研究生导师，硕士，研究方向为复杂机电系统一体化设计、伺服精密传动测试与控制技术，(E-mail)fanyx@njust.edu.cn。

TH166；TG506

A