复杂生产过程故障修复紧迫性分级研究*

谢 旺，袁逸萍，李晓娟，李华华

(新疆大学 机械工程学院,乌鲁木齐 830047)

复杂生产过程故障修复紧迫性分级研究*

谢 旺，袁逸萍，李晓娟，李华华

(新疆大学 机械工程学院,乌鲁木齐 830047)

复杂生产过程中受不确定性扰动因素的作用不可避免的会导致作业车间资源的退化、故障以及失效，针对故障资源修复顺序对多资源耦合的复杂生产系统性能(如交货期、生产成本等)的影响，引入复杂网络理论构建复杂生产作业车间网络模型，对生产特性和网络拓扑特性进行深入研究，对资源的故障修复进行紧迫性分级。综合考虑影响故障修复紧迫性的三个因素：是否发生在关键路径上、不可替代程度、故障节点的网络重要度，采用模糊综合评判的方法，将故障节点分为紧急、严重和一般三个层次，并计算出具体的紧迫度值。该模型为故障修复策略提供新的视角，为科学决策修复顺序提供理论依据。最后通过仿真实例验证了该方法的可行性。

复杂生产过程；故障修复；紧迫性分级；模糊综合评判

0 引言

在复杂制造系统中，存在多个相互依赖的工序，即使一个资源(如：设备、工装、工作站等)出现了故障也会直接影响上下游工序的活动和其他资源的任务进而可能导致资源的相继故障，严重的可能导致整个生产系统的瘫痪[1-2]。故障的及时修复保证生产系统平稳运行，提高生产系统的鲁棒性[3]，降低故障对生产性能(完成时间、生产成本)的影响，因而对故障修复进行紧迫性分级研究具有重要的现实意义。众多学者对作业车间故障修复做了大量的研究[4-6]，主要基于状态维修的现代维修策略(CBM)以及预防性维修(PRM)，对故障控制以及预防能够起到一定的作用，然而这些方法并不适用于新兴的复杂生产系统，预防性维修能够起到一定的预防作用，同时也可能导致大量资源的浪费。部分学者对制造系统故障级联效应[7]，制造系统鲁棒性[8]，制造系统的静态结构、动态行为以及拓扑结构[9-10]做出了一定的研究，然而对于复杂制造系统中故障的特性还缺乏深入研究。

因此，本文针对复杂生产过程中遭受不确定性扰动因素的作用(如：设备故障、紧急插单、工艺路线变更等)而导致的资源故障，对制造网络拓扑特性和生产特性深入分析，确定影响故障节点修复紧迫性的因素，采用模糊综合评判[11]的方法对故障节点的修复进行紧迫性分级，并计算出具体的紧迫度值，为科学决策故障修复顺序提供依据和支持。

1 构建复杂制造网络模型

1.1 复杂制造网络模型的描述

复杂网络是对复杂系统的一种抽象描述。以制造资源为节点，工艺路线为连边，工序优先关系为连边的方向，定义有向加权网络CMN=[R,E,W,S]。其中，R为资源节点集合；E为连边的集合；W为边权的集合，表示制造任务占用制造资源的时间；S为任务集合。节点间连边规则如下：

(1)同一个任务的工序一般存在时间上的先后约束，因此，同一个任务中的不同工序一般不可以同时进行加工。在这种情况下，这个任务的工序所对应的所有资源构成一个完全连通子图。

(2)不同任务的不同工序之间往往可能会出现抢占同一个资源的情况，在这种情况下将该资源加入每一个单一任务所对应资源的完全连通子图。

为了清晰描述制造网络由二维网络向一维网络投影，即工序层向资源层的映射，如图1所示。图1a是描述制造网络的双粒子图，当一项工序需要占用不同的资源时，它们之间都连接一条边，同时两个资源之间也连接一条如图1b所示的边。

(a)任务-资源二分图

(b)任务-资源映射图1 复杂制造网络映射关系图

1.2 网络化特征提取

(1)节点度

入度：kin表示在CMN中有多少上游节点直接与该节点相连，表示制造资源节点的加工对象范围，如公式(1)所示。

(1)

式中，Eji表示其他节点j汇入Vi边的数量。

出度：kout表示在CMN中有多少下游节点被直接连接到所观察的节点，表示制造资源节点加工能力的影响范围，如公式(2)所示。

(2)

式中，Eij表示节点Vi汇入其他节点j边的数量。

(2)节点强度

入强度Sin：反映制造单元承担的任务量，如公式(3)所示。

(3)

式中，Eji表示由节点j汇入节点Vi工序的数量，Wji为相应的权值。

出强度Sout：反映制造节点加工能力的影响程度，如公式(4)所示。

(4)

式中，Eij表示资源节点Vi汇入节点j工序的数量，Wij为相应的权值。

(3)聚类系数

聚类系数是指某个节点与其邻居节点间相互连接的紧密程度，可以反映制造网络中资源节点关键程度的大小，如公式(5)所示。

(5)

式中，ki表示与节点i有连边的节点的数目，Ei表示与i节点的邻居节点有关系的数目。

2 故障节点修复紧迫性

2.1 故障维修紧迫性的因素

综合考虑生产特性和制造网络特性对故障节点修复紧迫性的影响，影响故障节点修复紧迫性的因素包括三个方面：是否发生在关键路径上、不可替代程度、制造网络节点的重要度。

(1)是否在关键路径上

在复杂生产作业车间(Job-Shop)中关键路径是车间调度可行方案中工序间无时间间隔的最长路径，其距离与最大完工时间对应，关键路径中的工序为关键工序，通常分布在若干资源节点中。关键路径在Job-Shop中的特殊地位，决定了其为故障修复策略中重点考虑的一大因素。

(2)不可替代程度

不可替代程度是指资源节点故障修复中，资源节点不能用具有同等功能的资源节点替代的程度。资源节点不可替代的原因包括两个方面：一是该资源节点的功能独一无二无法用其他资源节点代替，如某种特种加工；二是企业车间中已有可用于替代的资源节点的数量和比率也影响资源节点的不可替代程度。

(3)制造节点的网络重要度

制造节点的网络重要度是指资源节点在制造网络中影响力的大小，节点的重要度越高，其对整个制造网络鲁棒性的影响越大。在制造网络中资源节点之间存在一定耦合关系，某些故障资源节点虽不在关键路径上但却能导致大量其他节点的相继故障，甚至整个制造网络崩溃。复杂制造网络模型中节点的重要度Vi定义如公式(6)所示。

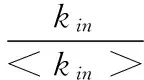
(6)

式中，<>表示对应统计特性参数的网络平均值；wki、wko、wsi、wso、wc为相应参数的权重。

2.2 影响因素标准化处理

三个影响因素评价指标体系中标准值的量纲不相同无法直接进行比较，先将其标准化，转化成无量纲标准化的数据再进行比较。采用直线型无量纲化方法，利用极差变换公式，如公式(7)所示。

(7)

式中，xi表示因素i在其所在评价指标下的特征向量或标度。其中，0≤ri≤1，该指标为正向指标，值越大说明该因素对紧迫性的贡献越大。

2.3 影响因素权值的计算

拟用最小平方和法计算各因素的权值，具体有两步：

(1)按照Saaty标度表两两比较各属性的重要性关系，建立矩阵A。

(8)

表1 两两比较的Saaty标度表

(2)通过两两比较的方法建立判断矩阵A时，可能会出现判断的一致性不协调问题，从而产生估计误差。为使估计误差尽可能小，拟用误差平方和最小，求权重(w1、w2、w3)，建立优化模型如式(9)所示：

(9)

构造拉格朗日函数L求解每个因素的权重w1、w2、w3。函数如公式(10)所示：

(10)

其中，λ为拉格朗日乘子。

函数L对wl求偏导，并令其为0，其中l=1，2，3，得到4个代数方程，表达式如式(11)所示：

(11)

2.4 紧迫性分级

模糊综合评判故障节点分级包括以下4个步骤：

步骤1：由2.3求解权值W=(w1,w2,w3)。

步骤2：确定影响故障节点维修紧迫性的因素集U=(u1,u2,u3)，u1为故障节点是否发生在关键路径上；u2为不可替代程度；u3制造网络节点重要度。对U中的每一个元素ui单独作一个评判f(ui)，就可以看作是从U～V的模糊映射，通过模糊映射f，可以推导出单因素评判矩阵(隶属关系矩阵)。

(12)

式中：R为从U到V的单因素评判矩阵，rij表示U中因素Ui对应于V中的Vj的隶属度，即某种资源节点在ui这个因素上能被评为Vj层级的隶属度。

步骤3：通过合成算子公式(13)，将W与R合成，从而得到故障节点k的评价向量Bk，然后确定故障节点k的类别。

(13)

步骤4：由评判故障节点的层级标准集合V=(v1,v2,v3)，v1为紧急；v2为严重；v3为一般。给定每个层级标准Vj，一个紧急度分值qj，qj表示第j个评判层级的量化值，由公式(14)，得每个故障节点k的需求紧迫度Pk的值。

(14)

3 实例验证

以某汽车制造企业A车间数据集作为研究实例，该作业车间共有10台机器(资源)Mi(i=1,2,…,10)，加工10类典型复杂工件，共有50道工序，加工之前工艺路线一定，每天工作8h。表2所示为各个产品工艺路径所占用的资源及资源对应的处理时间。

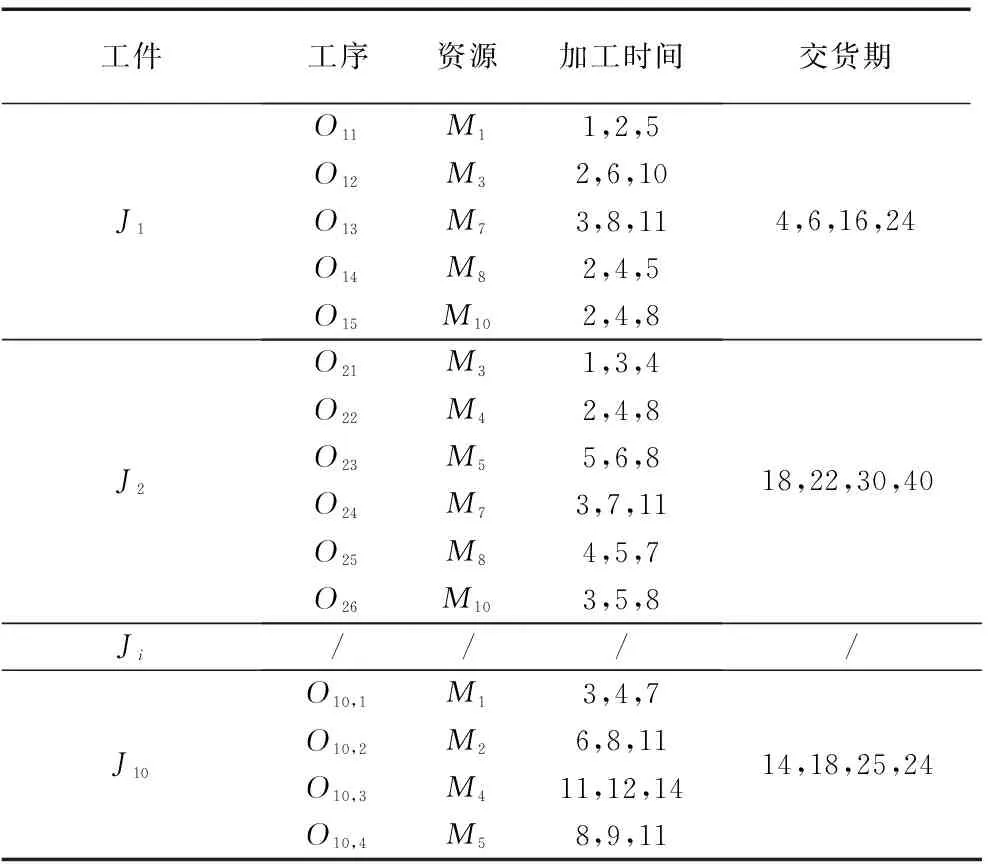
表2 不确定条件下10个工件10台机器部分工序资源时间表

J1表示工件1；O11表示第1个工件的第1道工序；加工时间(1，2，5)，1为最乐观时间，2为最可能时间，5为最悲观时间；交货期(4，6，16，24)，4为最小可接受时间，[6，16]为最满意时间区间，24为最大可接受时间。

3.1 各参数的计算

由基础数据统计可得每个资源分配的任务即工序量；由关键路径上的关键工序所对应的机器确定了资源节点是否处在关键路径上；由专家系统确定各个资源的不可替代程度；制造网络中重要度由公式(6)计算可得；参考文献[12]中公式(5)计算节点负载大小，节点负载是指所有待处理的工件占用第r个资源节点的时间总和与节点r额定工作时间的比值。以上计算结果如表3所示。并根据该车间MES系统真实反馈数据和实际观测情况，确定各节点在观察期内的故障状态,选取故障资源M5、M7、M10。

表3 资源节点各参数计算的结果

3.2 紧迫性计算

(1)按2.4中步骤1，即2.3中的计算方法算出各因素的权值W=(0.32，0.26，0.42)。其中，依据Saaty标度表，确定判断矩阵A。

(2)按2.4中步骤2，求取故障节点M5、M7、M10的单因素评判矩阵。

(3)按2.4中步骤3，通过合成算子将W与R合成，从而得到故障节点k的评价向量Bk。

(4)按2.4中步骤4，根据表4评价等级量化表对评判等级进行量化，并按公式(12)可以求的故障节点修复紧迫度值如表5所示，M7紧迫度>M10紧迫度>M5紧迫度与经验分析相符。

表4 评价等级量化表

表5 各故障节点修复的紧迫度值

4 结束语

本文以复杂制造系统为背景，从复杂网络理论这一新的角度出发，对复杂生产过程中多资源故障修复的紧迫性进行了研究。利用复杂网络理论分析了复杂制造系统的网络拓扑特性，提出了一种依据网络拓扑特性以及复杂制造系统固有的生产特性对故障资源修复紧迫性进行评估的方法。综合考虑了影响故障修复紧迫性的三个因素：是否发生在关键路径上、不可替代程度、制造网络节点的重要度，基于模糊综合评判将故障节点分为紧急、严重和一般三个层次并计算出具体紧迫度值。

在模糊综合评判模型中，部分物理量的确定受主观因素影响比较大，在模型的推广应用过程中需要采集专家经验并结合生产系统的实际情况来提高模型的准确度。本文建立复杂网络模型考虑了资源之间的耦合关系，对故障资源修复紧迫性做出静态评价，为基于生产特性和网络特性的故障修复策略研究奠定基础，为后续复杂制造系统故障修复策略的研究做准备。文章未考虑故障资源的动态行为，如故障的传播、连锁故障等对复杂制造系统性能的影响，笔者将在这一方面做进一步的研究。

[1] Becker T. Application of Topological Network Measures in Manufacturing Systems[M]. Dynamics in Logistics,Springer International Publishing, 2016.

[2] Kröning S, Denkena B. Dynamic scheduling of maintenance measures in complex production systems[J]. Cirp Journal of Manufacturing Science & Technology, 2013, 6(4):292-300.

[3] Becker T, Meyer M, Windt K. A network theory approach for robustness measurement in dynamic manufacturing systems[C]//Cambridge International Manufacturing Symposium,2013.

[4] Al-Najjar B, Alsyouf I. Selecting the most efficient maintenance approach using fuzzy multiple criteria decision making[J]. International Journal of Production Economics, 2003, 84(1):85-100.

[5] Lu K Y, Sy C C. A real-time decision-making of maintenance using fuzzy agent[J]. Expert Systems with Applications, 2009, 36(2):2691-2698.

[6] 陆中,孙有朝,吴海桥.基于着色随机时间Petri网的维修性建模方法[J].机械工程学报, 2011, 47(10):185-191.

[7] Jiang H,Gao J,Chen F. System failure analysis based on complex network theory [J]. Annual Reliability and Maintainability Symposium, IEEE,2009：176-181.

[8] Meyer M, Apostu M V, Windt K. Analyzing the Influence of Capacity Adjustments on Performance Robustness in Dynamic Job-shop Environments [J]. Procedia Cirp, 2013, 7(12) :449-454.

[9] Till Becker, Mirja Meyer, Katja Windt. A manufacturing system network model for the evaluation of complex manu-facturing system[J]. International Journal of Productivity and Perfor-mance Management, 2014, 3(63): 324-340.

[10] Beber M E, Becker T. Towards an Understanding of the Relation between Topological Characteristics and Dynamic Behavior in Manufacturing Networks [J]. Procedia Cirp, 2014, 19:21-26.

[11 ]谢季坚,刘承平.模糊数学方法及其应用[M].武汉:华中科技大学出版社,2013.

[12]李晓娟,袁逸萍,孙文磊.基于网络结构特征的作业车间瓶颈识别方法[J].计算机集成制造系统,2016, 22(4):1089-1096.

(编辑 李秀敏)

Complex Manufacturing Process Failure Repairing Urgency Classification Research

XIE Wang, YUAN Yi-ping, LI Xiao-juan，LI Hua-hua

(School of Mechanical Engineering, Xinjiang University, Urumq 830047, China)

Due to the effect of uncertainty disturbance factors, it is inevitable that some job shop resources in complex production manufacturing process will be degradation, failure and even invalidation. Aim for the failure repair sequence effects complex manufacturing system performance of multi resource coupling such as delivery date and production costs. Introduce complex network theory to construct complex job shop production network model, analyzing the production characteristics and the network topology characteristics deeply, classifying the repair urgency of failure resource. Considering the effect of three factors for fault repair urgency: whether it occurs in the critical path, degree of substitution and the importance of node failures in the network, using fuzzy comprehensive evaluation method, fault nodes into three level as urgent, serious and general. This model provided a new perspective for fault repair strategy and provided a basis theoretical for scientific decision repair sequence. Finally, case study validates the feasibility and effectiveness of the proposed method.

discrete manufacturing; failure repairing; urgency degree; fuzzy synthetic evaluation

1001-2265(2017)08-0064-04

10.13462/j.cnki.mmtamt.2017.08.016

2016-10-30；

2016-12-01

国家自然科学基金(51365054)；新疆维吾尔自治区自然科学基金(2014211A008)

谢旺(1991—)，男，湖南邵阳人,新疆大学硕士研究生，研究方向为计算机集成制造，(E-mail)xiewone@163.com；通讯作者：袁逸萍(1973—)，女，乌鲁木齐人，新疆大学教授，博士，研究方向为计算机集成制造，(E-mail)yipingyuan@163.com。

TH166；TG506

A