基于D-H矩阵的3-URS并联机构位姿误差建模与分析*

李春霞,张彦斐,宫金良

(山东理工大学 机械工程学院，山东 淄博 255049)

基于D-H矩阵的3-URS并联机构位姿误差建模与分析*

李春霞,张彦斐,宫金良

(山东理工大学 机械工程学院，山东 淄博 255049)

针对3-URS并联机构进行了运动学分析，利用D-H变换矩阵对其进行位姿分析，推导得到其运动学正解模型，在此基础上利用矩阵微分理论结合D-H矩阵得到了单条支链的位姿误差模型，最终得到全面考虑各关节处的误差来源(制造误差、安装误差、磨损误差等)的动平台位姿误差模型。应用该数学模型进行计算，并对3-URS并联机构的误差进行分析，给出了动平台末端误差随驱动角α1，β1的变化规律，通过该规律可得到误差敏感点，在工作过程中应注意避免。该误差模型的建立对3-URS并联机构的制造，及位姿控制的精度补偿有参考价值。

并联机构；D-H变换矩阵；位姿误差建模

0 引言

并联机构具有结构稳定、刚度大、承载能力强等优点，受到广大学者的关注[1-4]。目前并联机构的误差研究主要分为矢量法和矩阵法。谢福贵等[5]采用基于空间误差矢量链的误差建模方法，获得一种新型虚拟中心并联机构的误差模型。李嘉等[6]将各种误差源以统一方式描述，使其终端误差为所有广义误差的线性和。张立杰[7]，李永泉等[8]将环路增量法应用于多环路并联机构的误差分析。谭兴强等[9]针对单支链应用摄动法建立了一种六自由度并联机器人的运动误差模型。李瑞琴等[10]利用矩阵法建立了3-RSR并联机构的误差模型，并分析了各误差源对末端位姿误差的影响规律。

本文针对3-URS并联机构进行其误差分析，利用D-H变换矩阵建立其运动学正解方程，全面考虑各关节处的误差来源建立整机误差数学模型，并利用该误差模型分析驱动角度的变化对末端的位姿误差的影响规律，为后续该机构的样机标定及运动学补偿提供了理论基础。

1 3-URS并联机构正解建模

1.1 3-URS并联机构

图1所示的3-URS并联机构由动平台和静平台通过三条串联支链连接而成，其中三条支链呈120°对称分布，每条支链由U型副、下连杆、转动副、上连杆、球铰依次串联构成,驱动电机装在静平台的虎克铰两相互垂直的轴上。

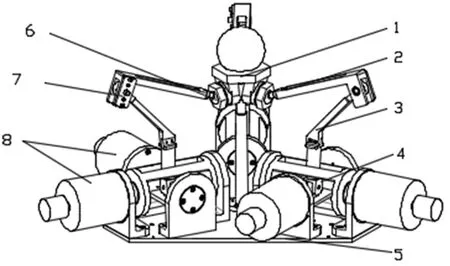
1.动平台 2.上连杆 3.下连杆 4.U型副 5.静平台6.球铰副 7.转动副 8.驱动电机图1 3-URS并联机构三维模型

1.2 3-URS并联机构正解模型

如图2所示，Ai(i=1,2,3)为U型副两转轴的交点，Bi为球铰S的中心点，且A1、A2、A3及B1、B2、B3所围成的三角形均为等边三角形，O、O1分别为两等边三角形中心点。

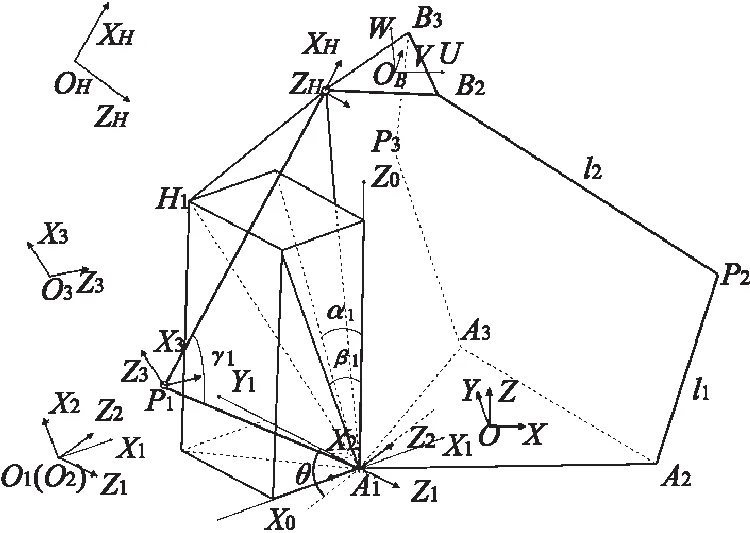
图2 3-URS并联机构坐标系示意图

采用D-H坐标法求解Si(i=1,2,3)，将支链简化为串联模型。静平台中心与Ai连线为连杆1，虎克铰拆分为两个轴线相交的转动副，虎克铰之间为连杆2，虎克铰和转动副之间为连杆3，上连杆为连杆4，相应的坐标系如图2所示，其中αi为轴ai绕X0轴的转角，βi为轴bi绕Z0轴的转角，αi和βi为驱动角，γi为向量PiAi和直线PiBi的夹角。表1给出了分支i各连杆的D-H参数和关节变量。

表1 Si支链D-H参数表

从连杆i到i-1的坐标系的变换矩阵Ai为：

其中，cθi=cosθi，sθi=sinθi。球铰坐标系OH-XHYHZH在静坐标系O-XYZ下的位姿转换矩阵为：

Ti4=A0iA1iA2iA3i

(1)

Ti4矩阵的第四列的1,2,3行数据即为球铰中心坐标，将表1中的各参数分别代入式(1)后可得单支链球铰坐标为：

其中，

通过上式可得动平台中心O1点的位置坐标为：

(2)

采用Z-Y-X欧拉角描述机构姿态角，即：

(3)

其中，

2 基于D-H矩阵的误差建模

在计算机构的误差模型时，将U型副和S副均等价为转动副参与计算，所以仅以转动副为例介绍运动副综合考虑各种误差源的误差建模过程。

如图3所示，理想情况下转动副运动过程中R1=R2，此时转动副的主动件和从动构件半径相同，两者完全贴合，且圆心重合，所以此时△L为零，即两者之间不存在任何偏差。但在实际情况下，由于制造误差、环境变化、疲劳磨损、安装误差等情况会使运动副间存在误差△L。

图3 运动副间隙示意图

上述间隙可看作D-H坐标的微小运动，则第i杆件的坐标系绕自身坐标轴有微小位移和微小转动的变换算子为：

(4)

其中绕坐标轴的平移分量和转动分量分别为：Ri=(dx,dy,dz)；Di=(δx,δy,δz)

将各关节误差综合后得到动平台的位姿，应用矩阵微分法[11]对式(1)微分得：

(5)

由式(1)、式(4)代入式(5)整理得:

(6)

将其展开可得单支链上的综合考虑多种误差源的末端球铰位姿误差为：

(7)

由式(2)、式(3)和式(7)综合考虑多种误差源的末端平台的位姿误差值为：

(8)

(9)

其中，

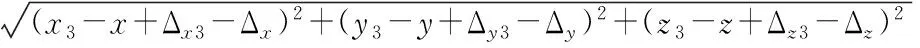
式(8)和式(9)表明了由各杆件坐标系微分运动得到末端平台位姿变化在静平台坐标系中的微分关系，可将机构由于制造误差，环境变化，疲劳磨损等情况会使运动副间存在的误差等价看做D-H坐标系的微分运动,则式(8)和式(9)即为该机构的综合考虑多种误差源的位置误差和姿态误差。

3 算例

给定并联机床几何参数a=240mm，l1=210mm，l2=190mm，θ=65π/180,驱动角αi∈(-π/4,π/4)，βi∈(-π/4,π/4)，PiAi到PiBi的转角范围为(0，π)。为更好的观察驱动角度的变化对末端误差的影响，将夹角的扩大两倍设为αi∈(-π/2,π/2)，βi∈(-π/2,π/2)。将各支链中的D-H坐标系的位置误差为[0.01 0.01 0.01]，转动误差为[0.01 0.01 0.01]。

图4、图5分别给出了驱动角α1、β1的变化对末端位姿误差的仿真计算结果。

图4 3-URS并联机构变化α1角位姿误差图

为便于观察各方向位移误差变化规律，将各方向误差适当放大后置于同一图中。

由图4a可知，随着α1的变化，该机构的位置误差大致呈线性变化，并随着α1的增大而增大。同时可知，在z方向的位移误差远大于其他两个方向的误差。由图4b可知，绕x方向的转动角的误差在-π/3的误差达到最大，在该点两侧依次减小，事实上绕x方向的误差值非常小，绕y方向的旋转误差最大值在-3π/8处，绕z方向的转动误差最大，同时在-π/3点处绕z方向的误差有最大值，而且和其他点的值有较大差距，所以在实际操作过程中应尽量避免该角度值。

图5 3-URS并联机构变化β1角位姿误差图

由图5a可知，其三个方向的位移误差大致呈不规则余弦变化，沿x方向误差最大，且在-3π/16处达到最小值，在3π/8处达到最大值，其在要求的工作范围内基本呈线性变化。沿y方向在-π/4和π/8处有最大值，在工作过程中要注意避免。沿z方向在要求的工作范围内基本呈线性变化，随着转角的增大误差增大。由图5b可知，在绕x方向的误差最大，且呈正弦变化规律，在-π/8处有最大误差值，绕y，z方向的误差均呈线性变化，且两者变化趋势相反，由于z方向误差变化范围较小，故在实际应用中可适度放弃该方向精度，向y方向误差较小的角度偏转。

4 结论

通过D-H矩阵法建立了3-URS的运动学正解模型，并在此基础上利用矩阵微分理论建立了每条支链的位姿误差模型并最终得到动平台的位姿误差模型。通过对误差模型的分析可得以下结论：

(1)该动平台的位姿误差模型综合考虑了运动副的制造、环境变化、疲劳磨损、安装等情况下使运动副间产生的误差,依据此模型给出了驱动角转动对末端平台位姿误差值的影响规律，并获得了对各个方向刚度的影响较大的角度值。

(2)通过对位姿误差模型的分析，为后续该机构的样机的标定、运动学补偿及实际操作中对误差较大点的规避提供了理论基础。

[1] 金振林,张金柱,高峰.一种消防六足机器人及其腿部机构运动学分析[J].中国机械工程,2016,27(7):865-871.

[2] 胡波,宋春晓,王安东,等.n(3-RPS)混联机构静力学和刚度模型[J].燕山大学学报,2015,39(5):408-413.

[3] 赵延治,王向南,任玉波,等.钳夹车并联起升机构分析与电液称重实验研究[J].中国机械工程,2016,27(4):1-6.

[4] Sébastien Briot,Victor Rosenzveig,Philippe Martinet,etc.Minimal representation for the control of parallel robots via leg observation considering a hidden robot model[J].Mechanism and Machine Theory,2016,12: 115-147.

[5] 谢福贵,刘辛军,陈禹臻.一种新型虚拟中心并联机构的误差灵敏度分析[J].机械工程学报,2013,49(17):85-91.

[6] 李嘉,王纪武,陈恳,等.基于广义几何误差模型的微机器人精度分析[J].机械工程学报,2000,40(8):20-24.

[7] 张立杰,李永泉.球面2-DOF冗余驱动并联机器人机构误差分析[J].机械工程学报,2013,49(7):148-154.

[8] 李永泉,张立杰,郭志民,等.基于D-H矩阵的球面5R并联机构误差建模及灵敏度分析[J].中国机械工程,2012,23(12):1470-1474.

[9] 谭兴强,张键,谢志江.风洞6_PUS并联支撑机器人运动误差建模与补偿[J].农业机械学报,2014,45(4):334-340,346.

[10] LI Ruiqin,Yang Bin .Error modeling of 3-RSR parallel robot based on D-H transformation matrix[J].Journal of Measurement Science and Instrumentation,2014,3:53-59.

(编辑 李秀敏)

Modeling and Analyzing of Position and Pose Error of 3-URS Parallel Mechanism Based on D-H Transforming Matrix

LI Chun-xia, ZHANG Yan-fei, GONG Jin-liang

(School of Mechanical Engineering, Shandong University of Technology, Zibo Shandong 255049,China)

The kinematics normal solution model of the moving platform of 3-URS parallel machine is established with D-H transformation matrix. Based on the model, the pose error model of single chain is established by matrix differential theory and D-H transformation matrix and the position and pose error model of the dynamic platform considering the error sources (manufacturing error, installation error, wear error, etc.) of the each joint are obtained by integrated each single chain. The variation law of the error of the moving platform 3-URS parallel machine with the drive angleα1andβ1is presented by analysis results from the mathematical model calculation. Error sensitive points are known by the law and in the actual operation they should be avoided. The results have reference value to the manufacture of 3-URS parallel mechanism, precision compensation of pose Control.

parallel mechanism；D-H transformation matrix；modelling of position and pose error

1001-2265(2017)08-0048-03

10.13462/j.cnki.mmtamt.2017.08.012

2016-10-16；

2016-11-05

国家自然科学基金项目(61303006)；山东省优秀中青年科学家科研奖励基金项目(BS2012ZZ009)

李春霞(1991—)，女，山东日照人，山东理工大学硕士研究生，研究方向为并联机器人， (E-mail)1039661855@qq.com；通讯作者：张彦斐(1977—)，女，河北衡水人，山东理工大学副教授，博士，研究方向为机器人设计与优化理论，(E-mail)gjlwing@sdut.edu.cn。

TH166;TG659

A