树状结构算法的介绍及其在生活中的应用

王维烨

摘要：本文主要介绍了数据结构中的各种树状结构，重点介绍了二叉搜索树，其他还包括平衡二叉树，红黑树，霍夫曼树以及堆。此外，本文详细解释了二叉搜索树的操作的时间复杂度。同时，我们将介绍各种树形结构在生活中的应用。

关键词：算法；树状结构；应用

中图分类号：TP312 文献标识码：A 文章编号：1007-9416（2017）05-0147-02

在计算机世界中，有各种各样的抽象数据结构，包括数组，队列，堆栈，链表等。这些数据结构都可以转换到现实生活中的各种问题中去，以此能够高效的解决一些问题。在这些数据结构中，被使用的较为广泛的无疑是树状结构。本文就将详细介绍一下树状结构。

所谓树状结构，就是将信息存贮在节点之中，节点与节点之间用边链接起来的结构。一颗二叉树由结点的有限集合组成。这个集合可以由一个根节点和两个不相交的二叉树组成，这两颗二叉树分别成为这个根节点的左子树和右子树。关于树状结构其他种类更多的结构介绍，我们将在下文中一一阐述。

树状结构在现实生活中的使用也相当广泛。从计算机网络到数据库实现，树状结构无时无刻的在提高我们的工作效率。本文也会介绍其在生活中的应用，以引发读者对计算机科学的兴趣。

1 二叉检索树

我们首先介绍一下树状结构中最为简单也是最为常见的一种树：二叉检索树（Binary Search Tree）。

1.1 定义

首先我们介绍一下二叉检索树，明确一下它的定义。

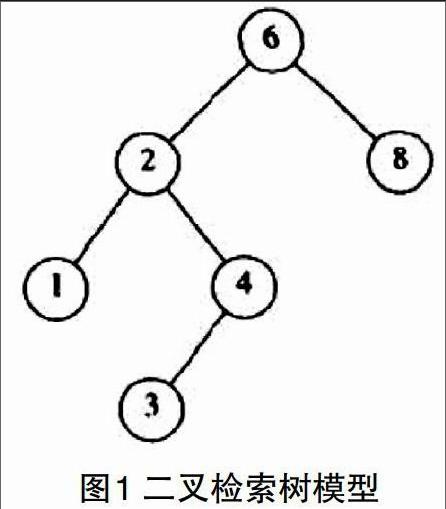
所谓二叉检索树，就是满足一下条件的一棵二叉树：任意一个结点，设其值为K，则该节点的左子树中任意一个結点的值都小于K；该结点右子树种任意一个结点的值都大于或等于K。如图1所示。

同时，任意一个结点都有其深度，我们定义为根节点到该节点的路径长度。而BST的高度就是最深深度加1。

1.2 二叉检索树的搜索

对于一棵二叉检索树而言，其最重要的功能就是能够快速的找到某一个节点的值。假设我们从根节点开始，在BST中检索K值。如果根节点存储的值为K，则检索结束。如果不是K，则必须检索树的更深一层。BST检索的优势在于只需要检索两棵子树的其中之一。如果K小于根节点的值，则只需要检索左子树，反之则检索右子树。这个过程将会一直持续到K被找到，或者到一个叶节点（没有子树）为止。如果到了一个叶节点，依然没有发现K，则表示K不在该BST中。

搜索所消耗的时间取决于该结点被找到的深度。我们思考一下在一般的情况下，我们需要往下寻找直到一个最深叶节点才能够停下。那么这时候，我们的时间代价就是该BST的高度。对于有n个结点的二叉树，如果它是平衡的，那么他的高度就为logn。因此在平均情况下，我们搜索功能的时间复杂度为O（logn）。

1.3 二叉检索树的插入

这里我们先做一个简单的假设，我们要插入的节点的值K与BST中任意一个节点的值不重复。我们插入一个节点的时候，我们需要找出它必须放在树结构的什么地方。这就会把它带到一个叶节点（子树数量为0的节点）或者一个在待插入的方向上没有子节点的分支节点（子树数量为1的节点）。我们记录该节点为R，然后我们将包含值K的新节点作为R的子节点加上去，就完成了插入操作。

与搜索类似，插入操作的时间代价依赖于R的深度。因此，在平均情况下，插入操作的时间复杂度为O（logn）。

1.4 应用

二叉检索树在生活中应用相当广泛。首先，二叉检索树是其他平衡二叉树的基础，例如AVL树，红黑树等。此外，就其本身而言，也在日常生活中体现了自己的价值。其中最典型的就是路由器中的路由搜索引擎，查找一条指定的路由最坏情况下最多只需要查找31次。

虽然二叉检索树在树中的地位相当的高，但是其更大的用处在于衍生了很多的平衡二叉树，这些树在我们现实生活中大发光彩。下面我们也会介绍到，但在介绍的过程中，我们不再详细说明其各种操作的原理以及时间代价了。一方面其复杂程序不是本文可以说明清楚的，另一方面我也希望将文章的重点放在应用这一角度。

2 堆

2.1 定义

堆由两条性质来定义：首先，它是一棵完全二叉树。其次，堆中存储的数据是局部有序的，也就是说，节点存储的值与其子节点存储的值存在着某种关系。这种关系可以分成两类，这两类关系也决定了两种不同的堆。

最大堆：任意一个节点的值都大于或者等于任意一个子节点的值。根节点存储着该树中所有节点的最大值。

最小堆：任意一个节点的值都小于或者等于任意一个子节点的值。根节点存储了该树中所有节点的最小值。

这里我们需要弄清楚他和BST的区别。BST是定义了一组完全排序的节点，左边节点的值都比右边节点的值小。而堆仅仅实现了局部排序，当一个节点是另一个节点的子节点时，才可以确定这两个节点的相对关系。

2.2 应用

堆在生活中的应用非常广泛，最为常见的两个就是排序和优先队列。

我们将一组无序的数列从小到大进行排列，就需要使用最大堆。我们知道根节点存储着该树中所有节点的最大值，因此我们不停的取出堆树的根，就能够得到一个有序的数列。在取出根之后，我们根据最大堆的性质，对这个堆进行转换（使其有一个新的根），这个操作的耗时非常少，因此堆排的效率还是非常高的。

优先队列的应用更为广泛。比如，我们工作时通常会先选择那些最为重要最为紧急的事件来先做，而不是那些很早就安排下来的任务。我们可以将这些任务建立起一个堆的模型，使用最大堆，节点存储的值就是任务的紧急程序。每一次做完一个任务，我们都能马上知道下一个紧急的任务是什么，这就是堆的用处。

3 Huffman编码树endprint

3.1 定义

首先我们要知道一个叫做Huffman编码的东西。他将会为字母分配代码，代码长度取决于字幕的相对使用频率或者“权重”。每个字母的Huffman编码是从Huffman树的满二叉树种得到的。Huffman编码树的每个叶节点对应一个字幕，叶节点的权重就是它对应字幕的出现频率，具体如图2。

我们在为每一个字母编码时，从根节点开始，到某一个叶节点结束经过的路径就是其编码，往左则为0，往右则为1。上图中，D的编码就是101，K的编码就是111101。可以看到，使用频率越小的字母编码越长，而使用频率较大的字母编码也较短。这是符合我们平时的生活规律的，越是常见的东西，我们就越是希望能够用简单的名字来称呼它。

3.2 应用

Huffman树以及Huffman编码已经被广泛的运用在计算机通信以及解压缩这方面。在计算机通信中，我们需要节约通信的成本。对于使用频繁的字母以及单词来说，我们希望将其转换成简单编码，这样整个传输数据的大小就会有明显的减少，也能够提高传输的速度以及稳定性。

同时，在压缩这方面，其本身就希望将复杂的内容用简单的编码来表示。应用的原理和计算机通信是类似的，目前市面上较为常见的解压缩软件都应用了Huffman编码来实现。

4 平衡二叉树

对于平衡二叉树，最为常见的是AVL树和红黑数。两者在定义上都是比较类似的，区别就在于为了保持“平衡”而采用的操作。

4.1 定义

所谓平衡二叉树，顾名思义，就是平衡的二叉树。其可以看成是带有如下特性的BST：对于树结构中的每一个节点，其左右子树的高度最多相差一层。只要维持这个特性，如果树中一共包含有n个节点，那么它的深度最大为logn（如果不是平衡的，那么深度有可能是n）。这样一来，我们在最糟糕情况下的时间复杂度也是O（logn）了。而如果仅仅是BST的话，最糟糕情况下的时间复雜度为0（n）。

当然，为了保持平衡，我们在插入和删除一些节点之后必须更新这棵平衡二叉树。AVL树和红黑数的更新方法是不同的，感兴趣的读者可以自行研究。

4.2 应用

平衡二叉树一般用在开发环境中的各种库函数中以及操作系统中。在Java中，集合TreeSet和TreeMap，C++ STL中的set，map都是通过红黑树来进行管理的。除此之外，红黑书在操作系统中虚拟内存的管理这方面也有所作为。

5 其他的树状结构

除了上述的几种比较常见的树状结构之外，生活中还有许许多多其他的树被应用着。比如伸展树，B+树等。这些树的定义，结构和操作都相对而言比较复杂，因此不在本文中阐述。

参考文献

[1]Clifford A.Shaffer. Data Structures and Algorithm Analysis in C++ Third Edition[M].电子工业出版社，2013.endprint