海量信息中模糊数据定位数学模型设计

丁晓丽

摘 要： 海量信息中的模糊数据具有特征不确定性和发散性，对其准确定位的难度较大，因此提出基于支持向量机二次规划的海量信息中模糊数据定位数学模型设计方法。在凸空间内构造模糊数据定位的高阶线性微分方程，求得模糊数据定位的极大线性无关组，采用支持向量机模型求得数据定位的聚类中心，以聚类中心的邻域数据集为训练模板集，通过凸组合二次规划方法进行Lyapunove泛函，实现模糊数据定位。数据测试结果表明，采用该方法进行数据定位的精度较高，收敛性较好。

关键词： 海量信息； 数据定位； 数学模型； 微分方程

中图分类号： TN911.1?34； O29 文献标识码： A 文章编号： 1004?373X（2017）16?0026?03

Abstract： The fuzzy data in vast amounts of information has the characteristics of uncertainty and divergence， and its accurate positioning is difficult. Therefore， a design method of positioning mathematical model for fuzzy data in mass information is put forward in this paper， which is based on quadratic programming of support vector machine. The high?order linear differential equations for fuzzy data location are constructed in convex spaces to obtain the maximum linearly independent group for fuzzy data location. The support vector machine model is used to obtain the clustering center of data location. The neighborhood data set of the clustering center is taken as the training. The quadratic programming method for convex combination is adopted for Lyapunove functional to realize fuzzy data positioning. The data test results show that the this method has high accuracy for data positioning and perfect convergence.

Keywords： mass information； data location； mathematical model； differential equation

0 引 言

在云計算平台中，随着大数据信息的增长，大量的数据集合之间存在模糊性。数据集之间的差异性特征严重影响了数据的有效分类和定位识别。为了提高对大数据背景下海量信息中模糊数据的准确定位识别能力，需要构建模糊数据定位的数学模型，建立模糊数据定位的微分方程，对微分方程进行稳定解分析和收敛性判断[1]。高阶线性微分方程模型在应对大规模海量数据集的处理和训练上，有其独特的优势。制约高阶线性微分方程运算的一个重要难题是解决线性模型约束下随机泛函微分方程的超线性收敛性问题。在线性模型约束下运用高阶线性微分方程进行海量模糊数据定位，把海量模糊数据的定位问题转化为一个超线性收敛性问题[2]，优化海量数据分类和模式识别，研究数据定位的数学模型就是研究高阶线性微分方程的极大线性无关组收敛性问题。对此，本文提出一种基于支持向量机二次规划的海量信息中模糊数据定位数学模型设计方法，通过数学模型设计和数据测试分析，展示了本文设计的数据定位数学模型的优越性能。

1 数学模型构建

1.1 高阶线性微分方程分析

为了实现对海量信息中模糊数据定位数学模型的优化设计，首先进行大数据信息流拟合的特征聚类分析[3]。在凸空间内构造模糊数据定位的高阶线性微分方程。模糊数据定位和识别是建立在对数据信息流的时间序列分析的基础上的，通过对大数据信息流的特征参量提取，进行数据聚类的属性特征选择和搜索，计算数据聚类中心，实现数据的自动定位和识别，在Laplace凸优化空间内，构建模糊数据定位的高阶线性微分方程组合模型，表示为：

3 仿真试验分析

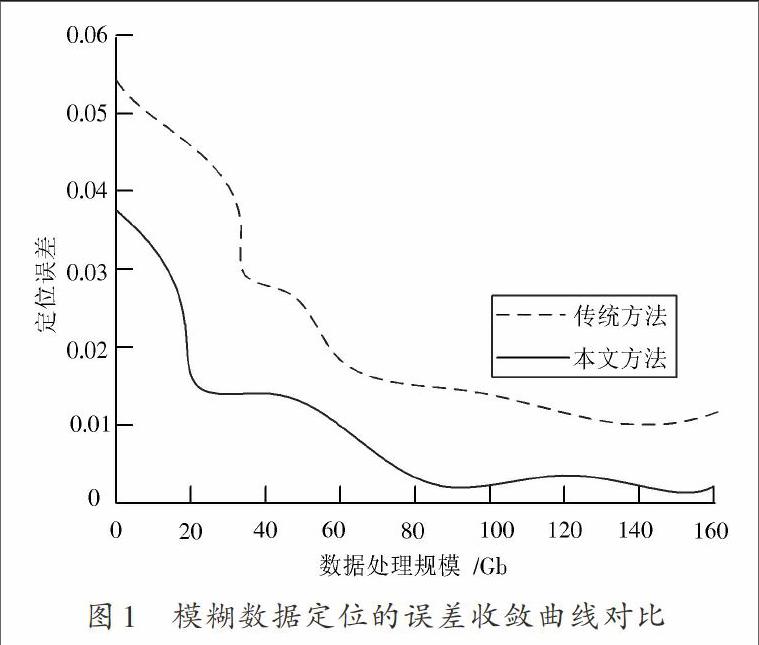
对海量信息模糊数据定位的仿真试验采用C++和Matlab 7混合编程设计，海量信息数据库使用MySQL。对海量数据的采样时间间隔为1.25 s，时间窗口系数[τ]为0.28，自适应参数[ε1=0.1]，迭代步长设定为24。根据上述试验参数设定，进行模糊数据定位分析，采用不同方法进行对比，得到数据定位的误差收敛曲线如图1所示。分析图1结果得知，采用本文方法进行海量信息的模糊数据定位的误差较小，收敛性较好，性能优于传统模型。

4 结 语

本文研究了海量信息中的模糊数据定位问题，由于模糊数据存在特征不确定性和发散性，对其准确定位的难度较大，本文提出一种基于支持向量机二次规划的海量信息中模糊数据定位数学模型设计方法。在凸空间内构造模糊数据定位的高阶线性微分方程，求得模糊数据定位的极大线性无关组，采用支持向量机模型求得数据定位的聚类中心，以聚类中心的邻域数据集为训练模板集，通过凸组合二次规划方法进行Lyapunove泛函，实现模糊数据定位。数据测试结果表明，采用该方法进行数据定位的精度较高，收敛性较好，具有较好的应用价值。

参考文献

[1] KAREEM I A， DUAIMI M G. Improved accuracy for decision tree algorithm based on unsupervised discretization [J]. International journal of computer science and mobile computing， 2014， 3（6）： 176?183.

[2] 尚朝轩，王品，韩壮志，等.基于类决策树分类的特征层融合识别算法[J].控制与决策，2016，31（6）：1009?1014.

[3] 余晓东，雷英杰，岳韶华，等.基于粒子群优化的直觉模糊核聚类算法研究[J].通信学报，2015（5）：74?80.

[4] 孙力娟，陈小东，韩崇，等.一种新的数据流模糊聚类方法[J].电子与信息学报，2015，37（7）：1620?1625.

[5] 林楠，史苇杭.基于多层空间模糊减法聚类算法的Web数据库安全索引[J].计算机科学，2014，41（10）：216?219.

[6] 蒋本立，张小平.大数据网络的均衡调度平台设计与改进[J].现代电子技术，2016，39（6）：62?65.endprint