单层单晶石墨烯与柔性基底界面性能的实验研究∗

仇巍 张启鹏 李秋 许超宸 郭建刚†

1)(天津大学力学系,现代工程力学天津市重点实验室,天津 300354)

2)(天津职业技术师范大学机械工程学院,天津 300222)

单层单晶石墨烯与柔性基底界面性能的实验研究∗

仇巍1)张启鹏1)李秋2)许超宸1)郭建刚1)†

1)(天津大学力学系,现代工程力学天津市重点实验室,天津 300354)

2)(天津职业技术师范大学机械工程学院,天津 300222)

(2017年4月12日收到;2017年6月9日收到修改稿)

单晶石墨烯具有更优异的力学及电学性能,有望成为新一代柔性电子器件的核心材料.因此,有必要从实验的角度精细分析化学气相沉积法制得的大尺度单晶石墨烯与柔性基底复合结构的界面力学行为.本文通过显微拉曼光谱实验方法测量了不同长度的单层单晶石墨烯/PET(聚对苯二甲酸乙二醇酯)基底的界面力学性能参数及其在长度方向上界面边缘的尺度效应.实验给出了石墨烯在PET基底加载过程中与基底间黏附、滑移、脱黏三个界面状态的演化过程与应力分布规律.实验发现,单晶石墨烯与柔性基底间由范德瓦耳斯力控制的界面应变传递过程存在明显的边缘效应,并且与石墨烯的长度有关.界面的切应力具有尺度效应,其值随石墨烯长度的增加而减小,而石墨烯界面传递最大应变以及界面脱黏极限则不受试件尺度的影响.

大尺寸单层单晶石墨烯,柔性基底,界面力学性能,显微拉曼光谱

1 引 言

石墨烯是由sp2杂化碳原子连接而成的蜂窝状的二维晶体材料,作为一种新型的纳米材料,因其具有优越的电学、热学、光学和力学性能[1,2],受到各领域科学家的追捧,逐步成为科学界的研究热点.特别是由于优异的电学性能和高柔性,石墨烯被认为是下一代制造柔性电子器件的新型材料之一.石墨烯在不同领域的潜在应用,使得对其力学性能研究尤为重要.为了进一步分析目前有关石墨烯力学性能的研究结果,Akinwande等[3]对现有关于石墨烯力学性能的理论与实验研究进行了总结与深入讨论.

由于各种尺寸的石墨烯将用于微电子器件新领域,如柔性电子元件、柔性应变传感器、纳米复合材料和电极材料等[4−6],而石墨烯与基底材料特别是柔性基底材料的界面性能与应变传递效率[7]是影响电子器件性能和质量的重要内部因素之一.同时,石墨烯的结构缺陷也会对电子器件产生影响.多晶石墨烯膜存在大量的晶界、位错等结构缺陷,例如由化学气相沉积法(CVD)制备的多晶石墨烯膜是由小晶畴拼接而成,从而在石墨烯内存在晶界[8].Zhang等[9]综合论述了缺陷和晶界对石墨烯膜的电学、光学和力学等性质的影响,同时石墨烯缺陷或晶界的数量、分布对其强度和断裂韧性也存在一定程度的影响,因此在微电子器件中,需要尽量减少这些缺陷与晶界.相对多晶石墨烯而言,理想的单晶石墨烯内不存在晶界,故而其性质与理论预期结果相近.为了充分发挥石墨烯的电学、力学、光学等性能,就需要制备并使用结构完整可靠的大尺寸单晶石墨烯[10].自2011年Robertson和Warner[11]通过CVD技术首次制备单晶石墨烯以来,制备高质量大尺寸单晶石墨烯的诸多技术瓶颈已被逐一突破.Lee等[12]在氢自终止的锗(110)表面制得芯片尺寸单晶石墨烯.Lu等[13]采用快速热处理的方法,使镍自主蒸发,从而获得任意基底的石墨烯,这种方法能快速制备石墨烯,且不需要对石墨烯进行转移.Wang和Zhao等利用CVD方法在铜基底表面制备了径向尺寸达5 mm的单晶石墨烯样品[14],并实现了石墨烯层数的可视化[15].基于以上所述,系统地测量不同尺寸单晶石墨烯与基底材料(特别是柔性基底材料)的界面力学性能,定量分析研究单晶石墨烯的尺寸效应是必不可少的.

有关界面力学性能、行为的实验研究需要采用高分辨、全场的实验力学手段.显微拉曼光谱是一种无损非接触、具有微米级空间分辨率的物性表征技术.由于诸如硅、金刚石、碳纳米管、石墨烯等材料的拉曼光谱对应力/应变较为敏感,使拉曼成为一种有效的力学测量方法[16,17].相比常见的光测方法[18−24],拉曼能够直接给出材料的应变/应力信息,适合于难以通过变形来表征关键参量的界面力学实验研究,已成为目前关于石墨烯界面力学行为实验研究的主要手段[25−30].

目前,有关石墨烯-柔性基底界面力学性能的实验研究大多是针对剥离法获得的小尺寸(微米量级)石墨烯和CVD法获得的大尺寸多晶石墨烯.例如Young课题组[25]用拉曼实验技术测量了机械剥离石墨烯的界面应力传递,得到单层石墨烯(12µm)与带胶的聚甲基丙烯酸甲酯(PMMA)基底界面应力传递的临界应变为0.4%—0.6%,基底间最大切应力为0.3—0.8 MPa,也测得了70µm石墨烯与基底间最大切应力为0.25 MPa[26];Jiang等[27]通过拉曼实验手段得到单层机械剥离石墨烯与聚对苯二甲酸乙二醇酯(PET)基底界面应力传递的临界应变为1.2%,界面间最大切应力为0.46—0.69 MPa.Zhang等[28]通过拉曼实验手段得到单层机械剥离石墨烯与PMMA基底界面应力传递的临界应变为0.7%,界面间最大切应力为0.45 MPa.Xu等[7,30]利用拉曼光谱原理,针对CVD法制备的单层多晶石墨烯材料,研究了石墨烯的切向界面边缘的力学性能和石墨烯尺寸对石墨烯-PET界面的最大切应力的影响,研究发现石墨烯界面传递最大应变以及界面切向脱黏应变极限不具有尺度效应,且分别为1.0%与2.0%;石墨烯在界面应变传递中存在边缘效应,并且与石墨烯的长度有关;界面的切应力具有尺度效应,其值随石墨烯长度的增加而减小,如长度为10 mm的石墨烯,其与基底间最大切应力为0.04 MPa,而长度50µm的石墨烯,其最大切应力为0.24 MPa.

本文在前期工作的基础上,围绕CVD法制备的单层单晶石墨烯开展实验工作,表征其与PET基底间切向的界面力学性能及其尺度效应.实验以显微拉曼光谱为手段,通过测量石墨烯/PET复合结构单轴拉伸-卸载过程中的石墨烯不同位置的应变信息,记录单层单晶石墨烯与基底在加载过程中的应力/应变传递过程,并进一步讨论分析拉伸过程中石墨烯应变变化规律,给出单层单晶石墨烯与PET基底间的界面力学关键参量,包括界面切应力、基底界面应力传递的临界应变、界面刚度、界面断裂韧性等.

2 样品与实验

本文实验所使用的单晶单层石墨烯材料是通过CVD法在铜箔基底上制备而成,得到的石墨烯单晶尺寸达到1 mm2.将制备的石墨烯通过湿法转移到厚度为100µm的PET薄膜表面[31].将表面附着完整单层单晶石墨烯的PET薄膜切割成(50×2)mm2长条形试件.将试件放置在低倍光学显微镜下,沿平行于试件宽度方向依不同间距切割获得不同长度的石墨烯,如图1.通过HIROX数字式三维视频显微镜测量获得机械切割石墨烯在PET表面留下的沟槽小于5µm,因此总体上不影响PET在轴向拉伸-卸载过程中的均匀变形.为研究石墨烯的界面力学性能及其尺度效应,本文设计了三种长度的石墨烯试件进行实验,即40µm石墨烯、100µm石墨烯和160µm石墨烯.

图1 石墨烯-PET试件结构示意图Fig.1.Structu ral d iagraMof graphene-PET speciMen.

实验中对PET长条形试件沿其长度方向进行步进位移的轴向拉伸加载.其中,PET属于柔性大变形材料,图2给出了通过万能试验机对PET标准试件轴向拉伸获得的应力-应变曲线,可见PET应变在0%—2.5%区间具有较好的应力-应变线性关系.因此,本文实验控制轴向拉伸加载应变上限为2.5%.此外,由于所测试的试件为长条形而非标准的哑铃形,而实验一般将两个卡具之间的位移视为试件整体变形(而非哑铃形试件的标距变化).为确定并修正长条形试件拉伸应变计算的误差,本文采用数字图像相关技术(DIC)[32,33]对长条形试件拉伸载荷下变形进行了标定(如图3(a)),并给出标定曲线如图3(b).其中,横坐标为采用卡具位移计算的试件长度方向的平均应变(名义应变),纵坐标为采用DIC测量得出的试件长度方向真实应变.数据处理时以该曲线为基准对拉伸实验数据的应变值给予修正.

本文实验对每个试件进行步进位移加载,步进步长最小约0.25%应变.在每步加载状态下,采用RenishaWInVia显微共焦拉曼光谱系统测量试件表面石墨烯不同位置的拉曼信息.拉曼采样点选取沿着样品长度方向(即拉伸方向)从石墨烯一侧边缘(即划擦划痕沟槽)至石墨烯正中心的中心线上.拉曼实验使用632.8 nMHe-Ne激光光源,不设置偏振方向,并选用100×物镜(N A=0.90)获得约1µm直径的采样光斑,拉曼取谱曝光时间为10 s,静态取谱模式,累计3次.

图2 (网刊彩色)PET标准试件轴向拉伸的应力-应变曲线Fig.2.(color online)Stress-strain curve of the standard PET speciMen.

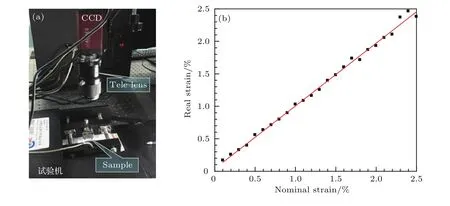
图3 (网刊彩色)PET试件拉伸实验标定与修正 (a)DIC测量系统;(b)修正曲线Fig.3.(color on line)D IC calib ration and correction of tensile test for PET speciMen:(a)DIC system;(b)correction cu rve.

3 实验测量结果

图4给出了本实验获得PET基底石墨烯试件典型的拉曼光谱曲线.由图可见,石墨烯具有明显的拉曼活性.其中,位于1600 cm−1附近的特征峰为G峰(包括一般在1585 cm−1的石墨烯G峰[34]和一般在1615 cm−1附近PET的G峰[35]),位于2650 cm−1附近的特征峰为石墨烯的2D峰[34].由于石墨烯和PET都具有G峰,尽管其位置有所差距,但由于PET的G峰信号远比石墨烯的强,因此难以精确地定量分析石墨烯G峰的频移变化.而明显可辨的2D峰是低维碳纳米材料(如碳纳米管、石墨烯等)独特的拉曼信息,而且其频移位置对应变具有较高的敏感度和线性度.因此,本文采用定量分析2D峰来表征石墨烯的应变信息.

理想石墨烯的应变与频移变化的线性关系能够用(1)式描述[36]:

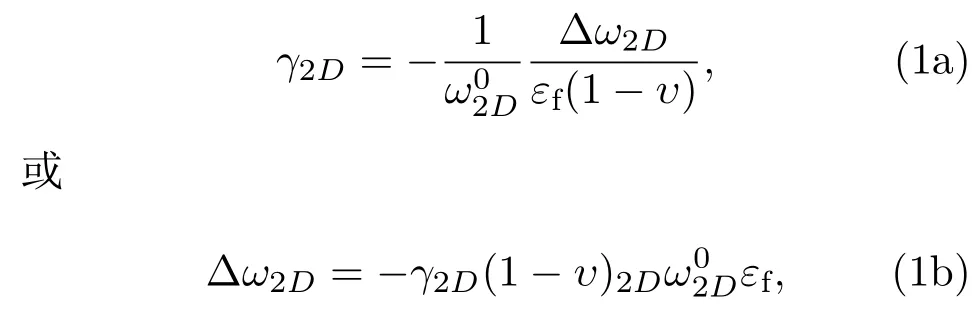
式中,角标2D表明关系式所表述的为2D峰的拉曼性质,γ被称为Grüneisen系数,ω0是在石墨烯的拉曼特征峰在没有变形状态下的最初位置,∆ω是石墨烯变形前后的频移变化量,υ是石墨烯泊松比,εf是石墨烯拉伸方向正应变.

图4 (网刊彩色)PET基底单层单晶石墨烯的典型拉曼光谱Fig.4.(color on line)Typical RaMan spectruMof the single-layerMonocrystalline graphene on the PET substrate.

基于(1)式给出的线性关系,就能够利用显微拉曼光谱测量石墨烯的应变,其中,Grüneisen系数γ是关键.然而,理论上得出的Grüneisen系数往往是个较为宽泛的范围,Mohiuddin等[36]在测得∂ω2D/∂ε≈ −64.0 cm−1/%下计算得到Grüneisen系数γ=1.99,而Sakata等[37]通过对碳纤维的实验计算得到Grüneisen系数γ=2.87.然而,Ni等[38]实验得到∂ω2D/∂ε≈ −27.1 cm−1/%,Yu等[39]在测得∂ω2D/∂ε≈ −7.8 cm−1/%,可见其实验测得的G rüneisen系数各有不同,而且都小于1.99.因此Grüneisen系数其具体值与测量系统和材料的个性密切相关,一般采用实验的方式标定取得[36−39].

图5给出了100µm石墨烯样品在加载时,被测单层单晶石墨烯的中心点的应变随基底应变变化曲线(其余两种试件的曲线与之类似不再罗列).由图可见,在基底由应变0%拉伸至2.5%的过程中,石墨烯样品测点的频移随着基底应变变化可以分成三个阶段,分别为线性变化段、非线性变化段、稳定段.由于石墨烯频移与其自身的应变呈线性关系,因此如图5给出的三个不同阶段即分别对应了石墨烯与基底之间界面的黏附(adhesion)、滑移(slide)、脱黏(debond)[29].其中,在线性变化段即石墨烯样品从初始载荷至0.5%基底应变过程中,2D峰频移变化量与基底应变呈良好线性关系,说明此阶段石墨烯与基底之间良好黏附并共同变形,基底应变即为石墨烯应变.因此可利用该段的线性关系标定石墨烯样品G rüneisen系数γ,再利用(1)式得出整个变形过程中石墨烯各测点的应变值(如图5右侧纵坐标所给出).

图5 (网刊彩色)100µm石墨烯中心点应变随基底应变的变化Fig.5.(color on line)Strain cu rve of central point on 100µMgraphene With the change of substrate strain.

为了直观地对比不同尺寸石墨烯在基底加载过程中的应变分布信息,图6(a)—(c)分别给出了40,100和160µm石墨烯沿载荷方向中心线上的应变分布曲线.其中,横坐标x表示无量纲化的测点位置,即以石墨烯样品中心点为零点,各个测点与中心点的距离除以石墨烯总长度为该测点的横坐标位置,即x=±0.5分别代表石墨烯的左右两边缘.此外,由于本文实验测量了中心点左侧各采样点的拉曼数据,图中中心点右侧各点数据为左侧数据做镜像映射给出.

4 分析与讨论

4.1 石墨烯的应变

由图6可见,在基底承受拉伸载荷的情况下,石墨烯应变分布曲线呈碗状.具体而言,同一试件在同一基底载荷下,从石墨烯边缘处向试件中心,石墨烯应变首先随位置变化而接近线性地增加,达到一定值后应变梯度急剧下降至基本为零,直至石墨烯试件中心应变保持稳定.本文从石墨烯边缘开始、应变逐渐增加的部分称为应变梯度区,将石墨烯中心两侧、应变基本保持不变的区域称为应变稳定区.同一试件在不同基底载荷下,随着基底应变的逐渐增加,应变梯度区的斜率逐渐增大,应变稳定区的应变值也随之增大,石墨烯应变分布的碗状曲线越来越深.然而,随着基底应变的线性增加至0.5%以后,应变梯度区的斜率与应变稳定区的应变值的增加不再呈线性且增速逐渐变缓,石墨烯应变的碗状曲线的重合度越高,直至基底应变≥2%后继续增加,而石墨烯应变分布曲线保持不变.不同样品的结果显示,石墨烯尺寸越小其应变分布曲线碗底宽度越小.

图6 (网刊彩色)不同PET基底拉伸载荷下(a)40µm,(b)100µm和(c)160µm石墨烯的应变分布曲线Fig.6.(color on line)The distribu tion cu rve of strain of d iff erent lengths of graphene in tensile load of PET(a)40µMgraphene,(b)100µMgraphene,(c)160µMgraphene.

4.2 石墨烯-PET界面力学行为

石墨烯与PET基底通过范德瓦耳斯力黏着吸附[25],实验时对PET基底施加位移载荷,应变通过界面传递到石墨烯上.对石墨烯单元体进行应力分析,建立其平衡方程.图7为石墨烯单元体的应力状态示意图,其中σf和εf分别为石墨烯拉伸方向的正应力和正应变,τi为界面切应力(ISS),t为石墨烯厚度,x为单元体在石墨烯长度方向上的相对位置.设定石墨烯为弹性变形,应用线弹性本构关系[25,29]:

其中,E为石墨烯的弹性模量.若单元体受力平衡,则两侧所受正应力的差由界面的切应力提供:

将(2)式代入(3)式有

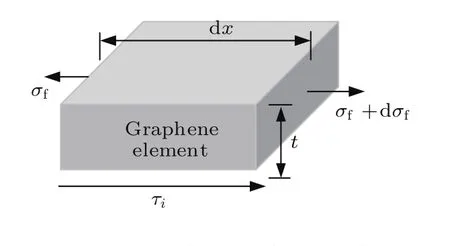
图7 石墨烯单元体应力状态示意图Fig.7.The Force balance of an eleMent of graphene.

利用(4)式,石墨烯与PET基底界面间的切应力大小正比于石墨烯的正应力一阶导数(即正应力的梯度),因此可以通过对如图6所给出的正应变分布曲线光滑处理后求导获得.本文石墨烯弹性模量与厚度取为E=1 TPa,t=0.34 nm[25,29].

以100µm石墨烯为例,图8给出了100µm基底应变0.5%时石墨烯沿载荷轴中心线上各点的正应力σf及界面切应力τi分布图.其中,黑色曲线为正应力分布,红色曲线为界面切应力分布.可见同一载荷下,石墨烯不同位置的切应力不一致、不均匀,在边缘处最大,在应力梯度区随着位置靠近试件中心而逐渐衰减,在应变稳定区基本为零.

图9给出了100µm石墨烯样品在不同基底应变下的界面切应力分布.由图可见,随着PET基底应变增加到0.5%时,石墨烯边缘处界面剪切应力率先达到最大值.PET基底应变继续增加,石墨烯从边缘处向中心方向各点逐渐到达最大切应变而发生脱黏,即脱黏区域逐渐增大.当PET基底应变到达2%以后,界面切应力分布保持不变,即石墨烯应变不再随基底变化,石墨烯完全脱黏.同时,可以得到100µm石墨烯最大切应力为0.247 MPa.

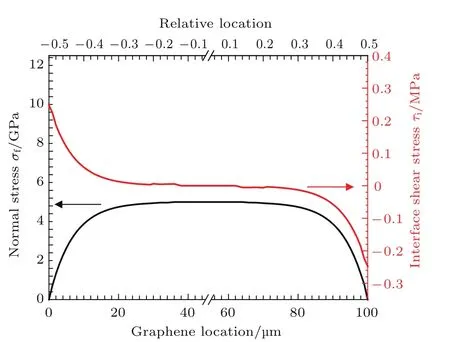
图8 (网刊彩色)100µm石墨烯试件在PET基底应变为0.5%时的正应力及界面切应力分布图Fig.8.(color online)The distribution curves of the norMal stress(b lack)and the interface shear stress(red)of 100µMgraphene when PET substrate under 0.5%tensile strain.

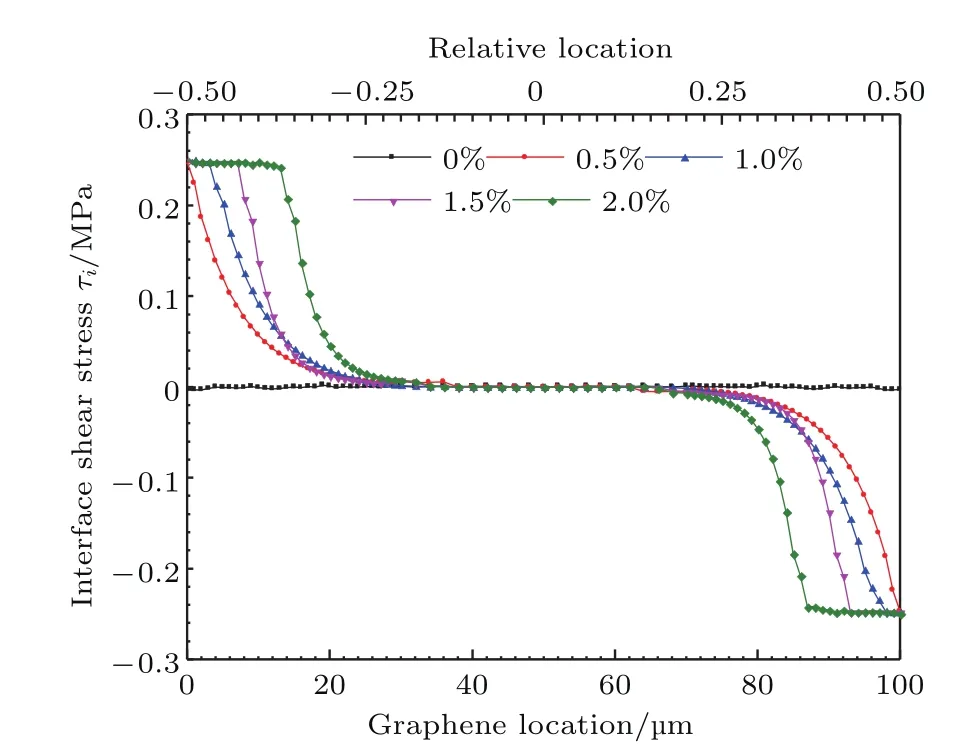
图9 (网刊彩色)100µm石墨烯不同基底载荷下界面切应力分布图Fig.9.(color on line)The d istribution curves of the interface shear stress on 100µMgraphene With d iff erent substrate strain.

以上分析表明,界面切应力将基底变形传递给了石墨烯.不同的基底变形,变形传递的效率也不同.仍以100µm石墨烯为例.由图5与图6(b)可知,在基底应变小于0.5%之前,石墨烯应变稳定区的应变值与基底应变相等,说明依靠范德瓦耳斯作用两者界面处于完全黏附状态,界面应力有效地将基底应变传递至石墨烯,图8和图9则展示了切应力主要是分布在石墨烯应变梯度区.在基底应变大于0.5%后,石墨烯的应变均小于基底应变,说明两者界面切应力已无法将基底应变完全传递给石墨烯,界面处于部分滑移状态.而当基底拉伸至应变大于2%时,石墨烯的应变分布曲线均不再发生变化,说明此时石墨烯与基底界面切向完全脱黏,基底增加的应变无法传递至石墨烯.将界面脱黏时刻所对应的基底应变称为界面切向脱黏应变极限εp[29],把界面切向脱黏之前石墨烯能随基底发生的最大应变定义为石墨烯的界面传递最大应变εmax.则通过分析100µm石墨烯界面切向脱黏应变极限为2%,界面传递最大应变为1.02%.同理,由图6可以得出,在基底应变为2%时(即界面脱黏之前),160µm和100µm石墨烯能随基底发生的最大应变为1.02%,而40µm石墨烯为0.99%,三者基本一致,这表明石墨烯试件尺寸的大小不影响界面传递最大应变.

图10 经典剪滞模型Fig.10.C lassical shear-lag Model.

在已有关于石墨烯与基底间的界面状态演化过程的相关研究中,不同的剪滞模型被用来描述石墨烯与基底间的应力与相对位移间的关系[27,28,40],其中对于黏附阶段的描述(特别是界面刚度的定义)是基本一致的.因此本文采用如图10所示经典的模型[27],其切应力与界面间相对位移间的关系由(5)式描述.其中,τ界面切应力,τmax为其最大值,δ表示界面的相对位移,K0为界面刚度.将该模型引入分析本文的石墨烯与基底间的切应力与相对位移间的关系,则(5)式和图10中的τ即为本文中的τi.在基底应变较小、石墨烯与基底间滑移位移小于δi时,由石墨烯的应力与位移边界条件,可以得到石墨烯应变εf与基底应变εm的关系为[27]其中,x仍为石墨烯各点的相对位置,L为石墨烯长度,β=E和t分别是石墨烯的杨氏模量和厚度.则由(4)式和(6)式得出石墨烯的切应力为

图11 (网刊彩色)石墨烯应变的解析拟合Fig.11.(color on line)Fitting resu lts of experiMental data by using analy tic Model.

由(7)式,随着基底应变增大,石墨烯切应力在其两端先到达最大值τmax,此时施加的基底应变用εc表示:

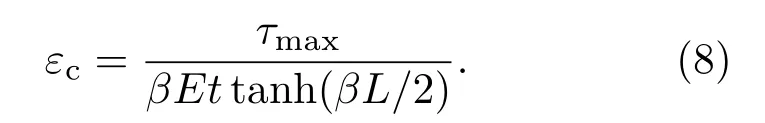
此外,基于经典剪滞模型可将断裂韧性(Gc)定义为

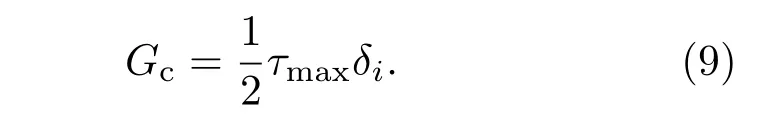
利用(6)式对于实验数据拟合,如图11.对于不同尺度的石墨烯试件,在基底应变在0.5%以内时,理论模型能够较好地拟合实验结果,说明此时基底应变为黏附阶段.当基底应变而超出0.5%以后,(6)式对实验数据难以良好拟合,可见其不能再用来预测后黏附阶段的石墨烯与基底间的界面出现性能.

利用黏附阶段数据拟合结果,得出40,100和160µm石墨烯试样各自的界面刚度分别为25.79,9.73,2.51 TPa/m.同时,计算得到断裂韧性分别为0.0028,0.0031,0.0072 N/m.其中,拟合获得的界面刚度与模型的选择无关;而由于不同模型表征断裂状态的差异性,石墨烯与基底间的界面断裂韧性将因模型的选择不同而不同.

4.3 石墨烯-PET界面尺寸效应

由图6并依上文所述,石墨烯应变沿载荷方向的分布存在应变梯度区及应变稳定区,并且应变梯度区与稳定区的长度在各载荷状态下是逐渐变化的.这表明在整个加载过程中,石墨烯界面在沿载荷方向上始终存在边缘效应.并且通过对比图6(a)—(c)可知,不同尺寸的石墨烯的边缘应变梯度区的长度是不同的,各自的无量纲长度也不同.即边缘效应对于不同尺寸的石墨烯的影响是不同的,这表明石墨烯的尺寸影响石墨烯的界面力学行为.

把应变梯度存在的区域长度(即边缘到应变稳定值90%位置的长度[29])称为临界长度lc,而临界长度lc与试件总长度l之比为相对临界长度λ,由该参数反映边缘效应的影响程度.λ越大,说明边缘效应的区域所占的比例越大,边缘效应的影响区域越大.图12(a)和图12(b)分别给出了各尺寸试件临界长度lc和相对临界长度λ随基底载荷变化的曲线.从图12可以看出,虽然各试件石墨烯尺寸不同,但一致性的规律是:随基底应变逐渐增大时,临界长度lc也增大,石墨烯与基底的界面需要越来越长的距离以实现载荷传递,直至达到其传递最大应变.然而,不同尺寸的石墨烯的差异在于相同的基底应变下各自的临界长度不一致.如在基底应变为0.5%时,100µm石墨烯临界长度lc为40µm,λ为0.40,而40µm石墨烯lc为20µm,λ为0.50;在基底应变为2%时,100µm石墨烯lc为70µm,λ为0.70,而40µM石墨烯lc为32µm,λ为0.80.

图12 (网刊彩色)不同尺寸单晶石墨烯试件(a)临界长度lc和(b)相对临界长度λ随基底载荷的变化Fig.12.(color online)The distribution curve of(a)critical length lcand(b)relative critical lengthλin d iff erent lengths With d iff erent substrate strain.

不同尺度石墨烯临界长度的差异性,导致在临界长度内传递变形的界面切应力分布及其极限的差异.图13给出了各尺度试件在脱黏时(基底应变2%)时的切应力分布.由于基底应变2%为各尺度试件共同的界面切向脱黏应变极限εp,此时界面达到界面传递最大应变εmax(约1%),界面切应力达到极限τmax.由图可见,长度为40µm的石墨烯其最大界面切应力τmax=0.38 MPa,长度为100µm的石墨烯τmax=0.25 MPa,长度为160µm的石墨烯τmax=0.19 MPa.实验表明,界面最大切应力值随石墨烯的长度的增加而显著减小.

图13 (网刊彩色)不同尺寸单层单晶石墨烯脱黏时界面切应力分布Fig.13.(color on line)The d istribution curve of interface shear stress on graphenes With diff erent lengths.

为了系统地讨论石墨烯尺度效应对界面力学性能的影响,表1列举了本文三个尺寸的单层单晶石墨烯实验与分析结果,并列举了其他小尺寸机械剥离的单晶石墨烯研究结果[25−28],连同前期Xu等[7,30]针对CVD单层多晶石墨烯的实验结果以及其他相关工作的数据.

由表1可见,与试件尺寸无关的量是界面传递最大应变εmax与界面切向脱黏应变极限εp,而受到尺寸影响的量包括临界长度lc、相对临界长度λ以及最大界面切应力τmax,且界面最大切应力值随石墨烯长度的增加而显著减小,相对临界尺寸随尺寸的增大而呈现减小的趋势.此外,界面刚度K0和界面断裂韧性Gc也存在明显的尺寸效应.将本实验结果与Xu等[7,30]针对单层多晶石墨烯的工作结果进行比较发现结果具有一致性,表明石墨烯与柔性基底的界面性能与石墨烯是否为单晶或多晶无关.与Jiang等[27]工作进行比较,本文得到的最大界面切应力结果偏小,这是因为Jiang等采用的是机械剥离的小尺寸(＜20µm)单层单晶石墨烯,而最大界面切应力存在尺度效应,且尺寸越小,对应的最大界面切应力越大,从而由于尺度效应导致了结果不一致.

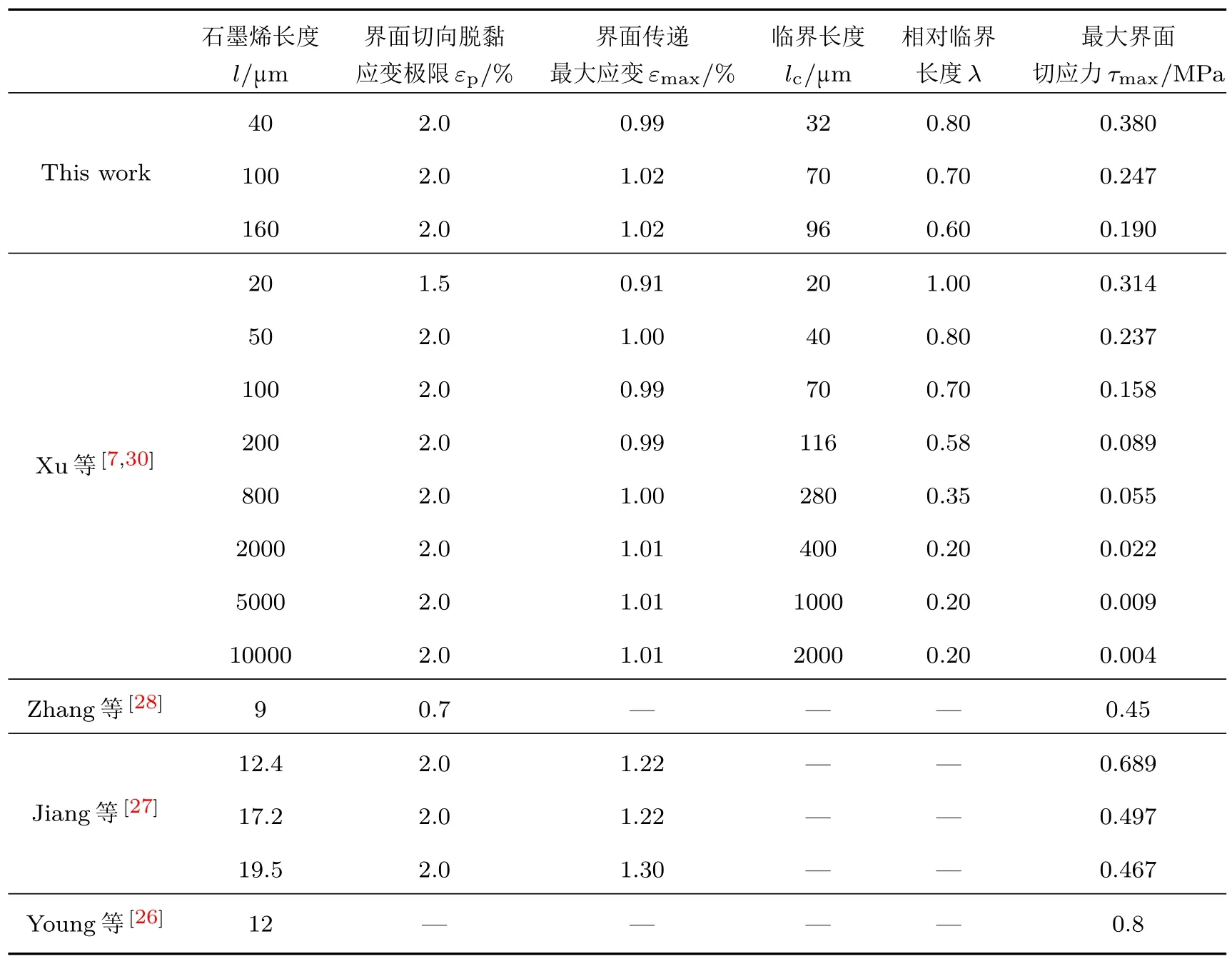
表1 不同尺寸石墨烯的界面力学参数Table 1.The interfacialMechanical paraMeters of graphene With diff erent lengths.

石墨烯的尺度效应可能与石墨烯的边缘的悬链有关[41,42].边缘的悬键与基底的结合,通常比范德瓦耳斯力作用强[41−43].尺寸小的石墨烯,石墨烯边缘悬键占石墨烯总体结构的比例大,对石墨烯与基底之间界面最大切应力的总体贡献较大;而随着尺度的增大,边缘悬键体量大幅下降,导致石墨烯与基底之间的最大切应力显著减小.通过计算,40µm石墨烯两侧边缘悬键约占总石墨烯键数的1.07×10−5—1.23×10−5,100 µm石墨烯悬键约占总石墨烯键数的4.26×10−6—5.52×10−6,160µm石墨烯悬键约占总石墨烯键数的2.66×10−6—3.07×10−6.可见,40 µm石墨烯与160 µm石墨烯所占比例相差一个数量级.

5 结 论

本文以实验为主要研究手段并结合理论分析,研究了大尺寸单层单晶石墨烯与柔性基底PET之间切向界面的力学性能及其在长度方向上界面边缘的尺度效应.三种长度的试件实验表明:单层单晶石墨烯的切向界面边缘的力学性能受尺度影响;随石墨烯尺寸的增加,其相对临界尺寸(边缘区域长度与总长的比值)出现减小的趋势;界面最大切应力值随石墨烯长度的增加而显著减小,且石墨烯试件尺寸的大小不影响界面传递最大应变.以上趋势与已有关于大尺寸单层多晶石墨烯和小尺寸单层单晶石墨烯的实验结果趋势基本一致.可见,在范德瓦耳斯力作用下的石墨烯与柔性基底的界面力学行为,存在明显的尺寸边缘效应,且与石墨烯是单晶或是多晶基本无关.

[1]Novoselov K S,GeiMA K,Morozov SV,Jiang D,Zhang Y,Dubonos S V,G rigorieva IV,Firsov A A 2004 Science 306 666

[2]BostWick A,Speck F,Seyller T,Horn K,Polini M,Asgari R,MacDonald A H,Rotenberg E 2010 Science 328 999

[3]Akinwande D,Brennan C J,Bunch J S,Egberts P,Felts J R,Gao H J,Huang R,K iMJ S,Li T,Li Y,Liechti K M,Lu N S,Park H S,Reed E J,Wang P,Yakobson B I,Zhang T,Zhang Y W,Zhou Y,Zhu Y 2017 ExtreMe Mech.Lett.13 42

[4]Bae S,K iMH,Lee Y,Xu X F,Park J S,Zheng Y,Balakrishnan J,Lei T,K iMH R,Song Y II,K iMY J,K iMK S,ÖzyilMaz B,Ahn J H,Hong B H,IijiMa S 2010 Nat.Nanotechnol.5 574

[5]Won S,Hwangbo Y,Lee S K,K iMK S,K iMK S,Lee S M,Lee H J,Ahn J H,K iMJ H,Lee S B 2014 Nanoscale 6 6057

[6]Ra ju A P A,LeWis A,Derby B,Young R J,K in loch I A,Zan R,Novoselov K S 2014 Adv.Funct.Mater.24 2865

[7]Xu C C,Xue T,Guo J G,K ang Y L,Qiu W,Song H B,X ie H M2015 Mater.Lett.161 755

[8]Banhart F,Kotakoski J,K rasheninnikov A V 2011 ACS Nano 5 26

[9]Zhang T,Li X Y,Gao H J 2015 Int.J.Fract.196 1

[10]Han J L,Zeng MQ,Zhang T,Fu L 2015 Chin.Sci.Bu ll.60 2091(in Chinese)[韩江丽,曾梦琪,张涛,付磊2015科学通报60 2091]

[11]Robertson A W,Warner J H 2011 Nano Lett.11 1182

[12]Lee J H,Lee E K,Joo WJ,Jang Y,K iMB S,LiMJ Y,Choi S H,Ahn S J,Ahn J R,Park MH,Yang C W,Choi B L,Hwang SW,Whang D 2014 Science 344 286

[13]X iong W,Zhou Y S,Jiang L J,Sarjar A,Mah jouri-SaMani M,X ie Z Q,Gao Y,Ianno N J,Jiang L,Lu Y F 2013 Adv.Mater.25 630

[14]Song Y N,Pan D Y,Cheng Y,Wang P,Zhao P,Wang H T 2015 Carbon 95 1027

[15]Cheng Y,Song Y N,Zhao D C,Zhang X W,Y in S Q,Wang P,Wang M,X ia Y,MaruyaMa S,Zhao P,Wang H T 2016 Chem.Mater.28 2165

[16]K ang Y L,Qiu Y,Lei Z K,Hu M2005 Opt.Laser Eng.43 847

[17]Cen H,Kang Y L,Lei Z K,Q in Q H,Qiu W2006 Compos.Struct.75 532

[18]Li X,Peng Y 2006 Appl.Phys.Lett.89 234104

[19]Li X D,Tao G,Yang Y Z 2001 Opt.Laser Technol.33 53

[20]Li X D,Wei C,Yang Y 2005 Opt.Laser Eng.43 869

[21]Zhang Q C,Jiang Z Y,Jiang H F,Chen Z J,Wu X P 2005 In t.J.P lastic.21 2150

[22]Wang M,Hu X F,Wu X P 2006 Mater.Res.Bu ll.41 1949

[23]Xu F,Li Y,Hu X,Niu Y,Zhao J,Zhang Z 2012 Mater.Lett.67 162

[24]Jiang H F,Zhang Q C,Chen X D,Chen Z J,Jiang Z Y,Wu X P,Fan J H 2007 Acta Mater.55 2219

[25]Gong L,K in loch I A,Young R J,Riaz I,Jalil R,Novoselov K S 2010 Adv.Mater.22 2694

[26]Young R J,Gong L,K in loch I A,Riaz I,Jalil R,Novoselov K S 2011 ACS Nano 5 3079

[27]Jiang T,Huang R,Zhu Y 2014 Adv.Funct.Mater.24 396

[28]Dai Z H,Wang G R,Liu L Q,Hou Y,Wei Y G,Zhang Z 2016 CoMpos.Sci.Technol.1 136

[29]Xu C C,Xue T,Guo J G,Qin Q H,Wu S,Song H B,X ie H M2015 J.Appl.Phys.117 164301

[30]Xu C C,Xue T,Qiu W,K ang Y L 2016 ACS App l.Mat.In terfaces 8 27099

[31]Suk JW,K itt A,Magnuson C W,Hao Y F,AhMed S,An J,Swan A K,Golderg B B,Ruoff R S 2011 ACS Nano 5 6919

[32]Kang Y L,Zhang Z F,Wang H W,Qin Q H 2005 Mat.Sci.Eng.A:Struct.394 312

[33]Zhang Z F,K ang Y L,Wang H W,Q in Q H,Qiu Y,Li X Q 2006 MeasureMent 39 710

[34]Ferrari A C,Basko D M2013 Nature Nanotech.8 235

[35]Tanaka M,Young R J 2006 J.Mater.Sci.41 963

[36]Mohiuddin T MG,LoMbardo A,Nair R R,Bonetti A,Savini G,Jalil R,Bonini N,Basko D M,Galiotis C,Marzari N,Novoselov K S,GeiMA K,Ferrari A C 2009 Phys.Rev.B 79 205433

[37]Sakata H,D resselhausG,D resselhausMS,Endo M1988 J.Appl.Phys.63 2769

[38]Ni Z H,Yu T,Lu Y H,Wang Y Y,Feng Y P,Shen Z X 2008 ACS Nano 2 2301

[39]Yu T,Ni Z H,Du C L,You Y M,Wang Y Y,Shen Z X 2008 J.Phys.Chem.C 33 12602

[40]Guo G D,Zhu Y 2015 J.Appl.Mech.82 031005

[41]Cong C X,Yu T,Wang H M2010 ACS Nano 6 3175

[42]Sasaki K,Sato K,Saito R,Jiang J,Onari S,Tanaka Y 2007 Phys.Rev.B 75 235430

[43]Nakada K,Fu jita M,D resselhaus G,D resselhaus MS 1996 Phys.Rev.B 54 17954

PACS:68.65.Pq,68.35.Ct,62.25.—g,78.30.—jDOI:10.7498/aps.66.166801

*Pro ject supported by the National Natu ral Science Foundation of China(G rant Nos.11422219,11672203,11372216,11472070).

†Corresponding au thor.E-Mail:guojg@tju.edu.cn

ExperiMental study on interfacialMechanical behavior of single-layer Monocrystalline graphene on a stretchab le substrate∗

Qiu Wei1)Zhang Qi-Peng1)LiQiu2)Xu Chao-Chen1)Guo Jian-Gang1)†
1)(T ianjin K ey Laboratory ofModern ExperiMental Mechanics,DepartMent ofMechanics,T ianjin University,T ianjin 300354,China)
2)(School ofMechanical Engineering,T ianjin University of Technology and Education,T ianjin 300222,China)

12 Ap ril 2017;revised Manuscrip t

9 June 2017)

Monocrystalline graphene is expected to becoMe a coreMaterial for the next-generation fl exible electronic device,oWing to its superior mechanical and electrical p roperties.Therefore,it is essential to analyze the interfacialmechanical property of the coMposite structure coMposed of large-scaleMonocrystalline graphene,prepared by cheMical vapor deposition(CVD),and fl exible substrate in experiMent.Recent years,Micro-RaMan spectroscopy has becoMe a useful method ofMicro/nano-mechanics for the experimental investigationson the properties of low-dimensionalnanomaterials,such as carbon nanotube(CNT),graphene,MolybdenuMdisulfide(MoS2).Especially,RaMan spectroscopy is eff ectively app lied to the investigations on themechanicalbehaviors of the interfacesbetween graphene fi lMsand flexib le substrates.AMong these researches,Most of the Measured saMp les are sMall-scale Monocrystalline graphene fi lMs which are Mechanically exfoliated froMhighly oriented pyrolytic graphite,a feWones are the large-scale single-layer polycrystalline graphene fi lMs prepared by CVD.There is still lack of study of the large-scale single-layermonocrystalline graphene.In thiswork,Micro-RaMan spectroscopy is used to quantitatively characterize the behavior of interface between single-layer Monocrystalline graphene fi lMprepared by CVD and polyethylene terephthalate(PET)substrate under uniaxial tensile loading.At each loading step froM0 to 2.5%tensile strain on the substrate,the in-p lane stress distribution of the graphene isMeasured directly by using RaMan spectroscopy.The interfacial shear stress at the graphene/PET interface is then achieved.The experiMental result exhibits that during the whole p rocess of uniaxial tensile loading on the PET substrate,the evolution of the graphene/PET interface includes three states(adhesion,sliding and debonding).Based on these results,the classical shear-lagModel is introduced to analyze the interfacial stress transfer froMthe flexib le substrate to the single-layer graphene fi lm.By fi tting the experiMental data,severalMechanical paraMeters are identified,including the interface strength,the interface stiff ness and the interface fracture toughness.The Raman measurements and resu lt analyses are carried out on the saMp les whose single-layer graphene fi lMs have diff erent lengths.It is shown that the stress transfer at the graphene/PET interface controlled by the van der Waals force has obvious scale eff ect coMpared With the graphene length.The interface strength,viz.theMaximuMof the interfacial shear stress,decreases With the increase of the graphene length.While the graphene length has no eff ect on the debonding strain or the strain transfer liMit of graphene/PET interface.Combining With other p revious studies of the large-scale single-layer graphene shows that theMechanical paraMeters of the interface between graphene and fl exible substrate have no relation noMatter whether the graphene isMonocrystalline or polycrystalline.

large-scale single-layer monocrystalline graphene,flexib le substrate,interfacial mechanical property,Micro-Raman spectroscopy

10.7498/aps.66.166801

∗国家自然科学基金(批准号:11422219,11672203,11372216,11472070)资助的课题.

†通信作者.E-Mail:guojg@tju.edu.cn

©2017中国物理学会C h inese P hysica l Society

http://Wu lixb.iphy.ac.cn