基于ab initio的BD+离子激光冷却理论研究∗

李亚超 孟腾飞 李传亮†邱选兵 和小虎 杨雯郭苗军‡赖云忠 魏计林 赵延霆

1)(太原科技大学应用科学学院,太原 030024)

2)(山西大学激光光谱研究所,量子光学与光量子器件国家重点实验室,太原 030006)

基于ab initio的BD+离子激光冷却理论研究∗

李亚超1)孟腾飞2)李传亮1)†邱选兵1)和小虎1)杨雯1)郭苗军1)‡赖云忠1)魏计林1)赵延霆2)

1)(太原科技大学应用科学学院,太原 030024)

2)(山西大学激光光谱研究所,量子光学与光量子器件国家重点实验室,太原 030006)

(2017年4月18日收到;2017年6月13日收到修改稿)

基于相关一致基组aug-cc-pV 5Z,采用内收缩多参考组态相互作用方法计算了BD+离子两个最低解离极限B+(1Sg)+D(2Sg)和B+(3Pu)+D(2Sg)对应的5个Λ—S态(X2Σ+,A2Π,B2Σ+,a4Π和b4Σ+)的势能曲线和跃迁偶极矩.根据计算结果,求解核运动的径向薛定谔方程得到相应电子态的振-转光谱常数、Franck-Condon(F-C)因子和振动能级辐射寿命.其中A2Π—X2Σ+的F-C因子 (f00=0.923)、辐射寿命(τ=235 ns)满足激光直接冷却的条件.因此,我们基于分子转动跃迁提出了一个可实现Dopp ler激光冷却的光循环方案:A2Π1/2(υ′=0)—X2Σ+(υ′′=0,1),其中υ′=0中包含2个转动能级,υ′′=0和υ′′=1中分别包含6个和4个转动能级.根据方案,模拟了激光冷却过程中的分子布居数动力学变化过程,并计算了初速度为100m/s的BD+,历经5.4Ms散射1150个光子可减速到4.6m/s、温度为13MK.

BD+离子,组态相互作用方法,光谱常数,Dopp ler激光冷却

1 引 言

过去30年中,激光冷却技术在原子领域中得到了飞速发展[1−3],由于分子复杂的内部能级结构使得这项技术在分子中一直未能得到发展.然而,分子具有更高的运动自由度和内部相互作用,异核分子还具有永久电偶极矩,所以激光冷却在分子领域中有着更广泛的应用,尤其是在量子计算[4]、超精细测量[5]、量子模拟[6]和化学反应动力学[7]等方面.2009年,美国耶鲁大学的DeMille等[8,9]利用激光冷却技术首次实现SrF分子冷却后,此技术已成为国内外原子分子物理学界的研究热点之一.

目前为止,实验上实现直接激光冷却的分子有YO[10,11],KRb[12]和CaF[13];实现光缔合冷却的分子有RbCs等碱金属分子[14];另外,许多小组理论上研究了RaF,A lH,A lF,BeF,MgF,BBr,BCl,LiBe,LiRb[15−21]和氢化物等分子[22]的激光冷却.在分子离子激光冷却方面,2011年Nguyen等[23]利用MRCISD和FCI(3e−)方法计算BH+和A lH+的势能曲面,提出了激光冷却方案并研究了粒子在冷却中的动力学过程.但Nguyen的方案中没有考虑自旋轨道耦合常数和X2Σ+态中振动能级υ′′=1—υ′′=0 之间的跃迁.BD+作为BH+的同位素分子离子,目前还没有理论计算和实验方面的相关报告.而在激光冷却中15BD+和15BH+分别属于费米和玻色体系,此外冷却后的BD+同位素分子可实现超精细分裂的测量,为研究原子核的电荷分布和低能情景下研究原子核的磁矩分布提供了合适的对象[24−26].

在本文中,我们利用高精度的内收缩多参考组态相互作用方法(icMRCI)计算了BD+离子X2Σ+,A2Π,B2Σ+,a4Π和b4Σ+的5个Λ—S态的势能曲线,获得了对应电子态的振动和转动常数.此外,我们计算了A2Π—X2Σ+的跃迁偶极矩(TDMs),Franck-Condon(F-C)因子、自发辐射寿命τ和A2Π态的自旋轨道耦合,并根据A2Π和X2Σ+态之间的跃迁特性,制定了详细的光学冷却方案:设计了激光冷却所需要的循环能级系统A2Π1/2(υ′=0)—X2Σ+(υ′′=0,1),模拟了冷却过程中粒子数的变化和光子的散射情况.

2 计算细节

2.1 Abintio计算

本文利用Molpro2012量化计算软件包[27]在C2v点群下0.6—8.0Å的核间距范围内研究了X2Σ+,A2Π,B2Σ+,a4Π和b4Σ+这5个Λ—S态的光谱性质.计算过程中,我们首先采用Hartree-Fock方法计算了BD+离子基态X2Σ+的波函数作为初始波函数,然后利用完全活性空间自洽场方法(CASSCF)对价电子波函数做态平均来进行优化.随后的MRCI计算中,我们将6个分子轨道放入活性空间,包括4个a1,1个b1,1个b2.为了提高势能函数的计算精度,我们考虑了核-价相关修正和Douglas-K roll哈密顿近似的相对论修正,最终选用了aug-cc-pV5Z-dk相关一致化基组.此外,我们计算了A2Π—X2Σ+的TDMs,基于势能函数的计算,我们用最小二乘法拟合得到了Re,ωe,ωeχe,Be,αe等光谱常数;通过LEVEL8.0[28]程序求解核运动的径向薛定谔方程得到了5个态的振-转能级、A2Π—X2Σ+跃迁的F-C因子和A2Π态低振动能级的辐射寿命τ.

2.2 速率方程模型

爱因斯坦系数Aυ′υ′′一般用来表征辐射跃迁概率,当Franck-Condon近似有效且不考虑空间简并时,它可以由下面的公式给出[29]:

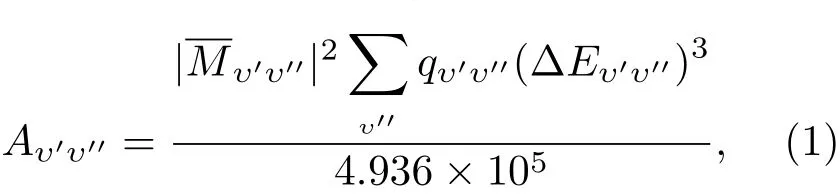
其中,υ′和υ′′分别代表上态和下态的振动能级;∆Eυ′υ′′是指上下态振动能级的能量差, 单位是cm−1;Mυ′υ′′是原子单位下的跃迁偶极矩;qυ′υ′′是指F-C因子.此外,系数B是由系数A计算得出:

式中ħ是普朗克常数,c是光速,ωυ′υ′′是跃迁频率,其中受激吸收系数Bυ′′υ′与受激辐射系数Bυ′υ′′相等.通过爱因斯坦系数和跃迁频率得出的速率方程中粒子数的变化可以很好地描述BD+粒子布居数[30].关于所选态i的粒子数Pi由下列公式给出:

其中,P代表在此模型中由N×N个振-转能级组成的粒子数矩阵向量;Aij,Bij和Bji分别对应爱因斯坦系数中的自发辐射、受激辐射和受激吸收过程;ρ(ωij)是频率为ωij的饱和光强谱能量密度.

3 结果与讨论

3.1 Λ—S态的势能曲线和光谱常数

BD+离子的第一解离极限B+(1Sg)+D(2Sg)包含1个二重态X2Σ+;第二解离极限B+(3Pu)+D(2Sg)包含2个二重态A2Π,B2Σ+和2个四重态a4Π,b4Σ+.势能曲线的计算结果如图1所示.图1中可以看到基态X2Σ+的平衡核间距Re在1.2Å附近,其主要的电子组态是(1σ)2(2σ)2(3σ)1,所占比重为93.41%.A2Π态在Re处的主要组分是(1σ)2(2σ)2(1π)1,所占比重为92.93%,它是由一个3σ轨道电子激发到1π轨道产生.

对于光谱常数,目前还没有BD+离子相关的理论计算和实验信息,但由于BD+和BH+是同位素分子离子,具有相同的核外电子排布,所以它们的势能函数相同.我们将基于图1拟合出的BH+的光谱常数在表1中列出,并给出RaMsay和Sarre[31]在1982年报道的BH+的实验数据、Nguyen[23]和K lein等[32]的计算数据与我们的结果做比较.本文获得X2Σ+态的Re为1.202798Å;Be为12.6296 cm−1;De为1240 cm−1;D0为1.94 eV,这与实验结果Re=1.20292Å;Be=12.6177 cm−1;De=1225 cm−1;D0=1.95±0.09 eV非常符合.对于A2Π态,Re为1.24761Å;Be为11.73865 cm−1;αe为0.46 cm−1与实验的Re=1.24397Å;Be=11.7987 cm−1;αe=0.4543 cm−1较为接近,ωe=2247.3 cm−1,D0=3.36 eV也与Nguyen等计算获得ωe=2245 cm−1,D0=3.35 eV比较接近,这也证明了我们计算数据的可靠性.表2中我们首次给出了BD+4个Λ—S态的光谱常数,由于b4Σ+态没有势阱,不存在束缚振动能级,所以它的光谱常数没有给出.此外,我们还计算了A2Π态的S—O常数Ω=12.99 cm−1,与文献中给出的实验值比较符合[33].

图1 (网刊彩色)BD+离子的5个Λ—S态的势能曲线Fig.1.(color on line)Potential energy curves of five Λ—S electronic states of BD+.

表1 BH+离子X2Σ+和A2Π 态的光谱常数Tab le 1.Spectroscop ic paraMeters of X2Σ+and A2Π states of BH+.

表2 BD+离子4个Λ—S态的光谱常数Tab le 2.Spectroscopic paraMeters of fourΛ—S electronic states of BD+.

3.2 跃迁特性

基于aug-cc-pV 5Z-dk基组,我们采用MRCI方法计算了A2Π—X2Σ+跃迁的TDMs,其随核间距变化的曲线在图2中给出.图2呈现了经绝对值处理后A2Π—X2Σ+态的TDMs曲线,很明显,在解离极限之前一直存在跃迁,在3Å处TDM逐渐趋向于0,说明之后无跃迁发生.对应到势能曲线上,3Å为A2Π和X2Σ+态的势阱的边缘位置.

A2Π(υ′)—X2Σ+(υ′′)跃迁的F-C因子在表3中列出,为了简化,υ′和υ′′只取到5.通常,我们更关心其对角线的值,F-C因子越大(接近于1),对应的两个态振动能级间的跃迁概率越高.为了更形象地表现F-C因子的对角化分布,在图3中绘制出立体直方图.A2Π (υ′=0)— X2Σ+(υ′′=0)跃迁的F-C因子(f00)等于0.923,这是建立冷却方案的先决条件.A2Π(υ′)—X2Σ+(υ′′)跃迁的自发辐射寿命在图4中展出,其中A2Π (υ′=0)— X2Σ+(υ′′=0)的τ为235 ns,根据分子满足激光冷却的标准[34].

表3 A2Π(υ′)—X2Σ+(υ′′)跃迁的 F-C 因子Table 3.F-C factors of A2Π(υ′)–X2Σ+(υ′′).

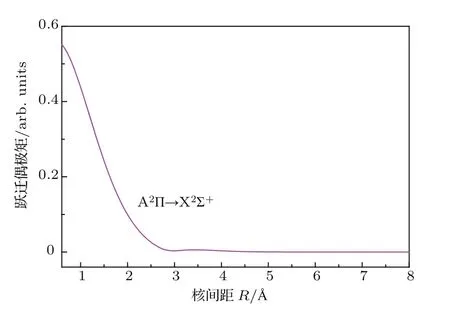
图2 A2Π—X2Σ+跃迁的跃迁偶极矩曲线Fig.2. Transition d ipole MoMents(TDMs)of A2Π–X2Σ+system.

图3 (网刊彩色)A2Π(υ′)—X2Σ+(υ′′)跃迁的 F-C 因子Fig.3. (color online)F-C factors of A2Π(υ′)–X 2Σ+(υ′′).

3.3 冷却方案

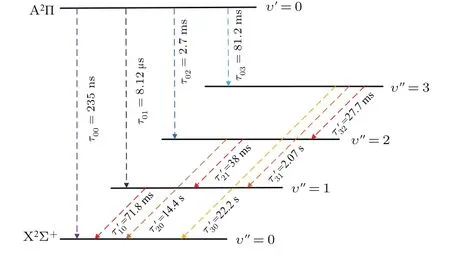
图4 (网刊彩色)A2Π和X2Σ+态振动能级的辐射寿命Fig.4.(color on line)Rad iative lifetiMes of vibrational levels for A2Π and X2Σ+states.

图5 (网刊彩色)A2Π1/2(υ′=0)—X2Σ+(υ′′=0)的能级跃迁示意图Fig.5.(color online)Energy level scheMatic diagraMshoWing transitions of A2Π1/2(υ′=0)–X2Σ+(υ′′=0).

对分子实现激光冷却,必须根据各能级之间的跃迁特性,构成闭合的循环跃迁结构.图5为我们设计的A2Π态在S—O耦合效应下A2Π1/2(υ′)—X2Σ+(υ′′)跃迁的光学冷却方案, 所涉及的能级主要是A2Π1/2态的υ′=0和X2Σ+态的υ′′=0的振动能级,其中每个振动能级中包含有转动能级.图中黑色的横线代表各转动能级,根据转动跃迁的选择定则:∆J=0,±1,其中0代表Q支,1代表R支,−1代表P支,而图中蓝色实线箭头代表Q支的跃迁,黑色虚线箭头代表P支的跃迁.双向箭头(阴影区域)是指激光激发受激跃迁能级(υ′=0—υ′′=0),这过程中的粒子变化包括自发辐射,受激辐射和受激吸收.其中4个过程中激光器的参数分别为λ00=375.8 nm,λ11=376 nm,λ12=376 nm,λ03=376.4 nm,入射光强为饱和光强时四束激光的谱能量密度ρ为4×10−19J/m2.

由于振动态之间跃迁没有严格的选择定则,对于粒子从能级υ′′=0吸收光子跃迁到υ′=0后,它除了可以跃迁到υ′′=0能级,还要考虑能量更高的υ′′=1能级,但根据前面的计算可知从υ′=0到υ′′≥ 2的能级的跃迁概率极小(比υ′=0—υ′′=0小约4个量级),因此计算过程中不做考虑.此外,υ′′=1上的粒子也会自发辐射到υ′′=0能级,这样就构成了光学的循环跃迁,为了提高冷却效率,我们在υ′=0—υ′′=1上增加4束再抽运激光:λ′00=402.8 nm,λ′11=403 nm,λ′12=403 nm,λ′03=403.4 nm,如图6. 其中υ′′=1中主要用到J′′=0,1,2,3这4个转动能级,υ′′=1—υ′′=0的过程只包含自发辐射.如上述表示相同,图6中黑色的横线代表各转动能级,蓝色实线箭头代表Q支的跃迁,黑色虚线箭头代表P支的跃迁,红色波浪线箭头代表R支的跃迁.

图6 (网刊彩色)A2Π1/2(υ′=0)—X2Σ+(υ′′=0,1)的能级跃迁示意图Fig.6. (color on line)Energy level scheMatic diagraMshoWing transitions of A2Π1/2(υ′=0)–X2Σ+(υ′′=0,1).

根据给出的冷却方案,λ00和λ03作为主激光,λ11和 λ12是辅助激光,λ′00,λ′11,λ′12和 λ′03为再抽运激光,假设只考虑λ00和λ03,υ′′=0中的J′′=1,2,4,5都将成为暗态,图6中用绿色和橙色的横线表示;在考虑了λ11和λ12后,J′′=1,2(绿色)能够参与跃迁,所以υ′=0-υ′′=0的4束激光是构成循环跃迁的必要条件.表4给出了计算中用到的爱因斯坦系数,为了方便识别,以υ′′=0,J′′=0,1,2,3,4,5;υ′=0,J′=0,1;υ′′=1,J′′=0,1,2,3为序标识1—12.通过解2.2节中的方程(3)求得各能级的粒子布居数,激发态粒子布居数求积分后乘以对应自发辐射系数(见表4)可得到冷却过程中的光子散射数.通常用于冷却的超声分子束的转动温度在10 K左右,开始冷却时υ′′=0振动能级上的四个转动能级从低到高的粒子数布局比例分别为:0.7,0.15,0.15和0.具体的模拟结果在图7中给出.Dopp ler冷却中,对于分子量大于20的分子,如果从室温环境冷却到约MK量级的超冷温度需要散射超过104个光子.而对于BD+分子,相对分子质量为12.825,不足20,BD+从300 K冷却到约MK量级温度需要散射8450个光子.对于我们的模拟结果,如图7所示,光子散射数随时间的增加呈指数增大,当BD+散射8450个光子时需要的时间为41Ms.

与YO分子相比,低温缓冲池中发射出的粒子初速度为70 m/s,温度为缓冲气体氦的温度3.5 K,从YO分子发射,减速到10 m/s,最终囚禁在磁光阱,需要经过89 cm的冷却路径.若BD+初速度也为70 m/s,那么它减速到10 m/s时俘获所经过的路程只有13.6 cm.对比SrF分子,从常温状态冷却到5MK需要散射40000个光子,SrF的分子量为106.618,大于20.所以我们设计的系统优势在于BD+离子属于分子量较小的粒子,冷却过程中不需要散射过多的光子,这就导致冷却时间会缩短,冷却装置的尺寸也会减小.此外,图6给出的方案中,粒子在各能级跃迁时会在υ′′=0中有J′′=4,5的暗态能级,此暗态会影响最终的冷却效率.但通过计算得出BD+散射8450个光子时的冷却效率为92%,因此,在实现激光冷却到约MK量级冷却的过程中暗态的影响不是很大.

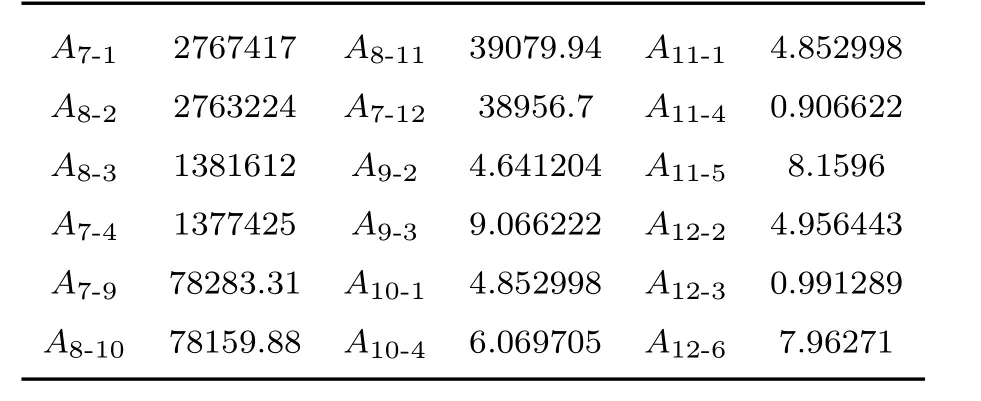
表4 模拟计算中所用的爱因斯坦系数Tab le 4.The Einstein coeffi cients used in the siMu lation calcu lation

图7 BD+光子散射数随时间变化的模拟结果Fig.7.P lot of the cycling-transition photon count for the BD+siMu lation resu lts.

4 结 论

本文利用MRCI/aug-cc-pV5Z-dk研究了BD+离子的X2Σ+,A2Π,B2Σ+,a4Π和b4Σ+电子态.给出了BD+的X2Σ+,A2Π,B2Σ+和a4Π态的光谱常数.此外,计算了A2Π—X2Σ+的跃迁偶极矩TDMs,并根据其结果给出了F-C因子、低振动能级的辐射寿命τ和X2Σ+态内部能级寿命τ′.最后,依据A2Π—X2Σ+的跃迁特性,提出了一个BD+离子的Dopp ler激光冷却方案,并根据粒子在循环跃迁中的动力学过程,计算了粒子布居数,给出了冷却过程中光子散射随时间变化的模拟结果:从300 K冷却到～MK温度需要散射8450个光子,历时41 ms,冷却效率92%,这对实验上实现BD+的激光冷却提供了有价值的参考.

[1]Chu S 1998 Rev.Mod.Phys.70 685

[2]Cohen-Tannoud ji C N 1998 Rev.Mod.Phys.70 707

[3]PhillipsWD 1998 Rev.Mod.Phys.70 721

[4]DeMille D 2002 Phys.Rev.Lett.88 067901

[5]F laMbauMV V,Kozlov MG 2007 Phys.Rev.Lett.99 150801

[6]Pupillo G,Micheli A,Büch ler H P,Zoller P 2009 Co ld Molecu les:Theory,ExperiMen t,App lications(Boca Raton:CRC Press)

[7]K reMs R V 2008 Phys.Chem.Chem.Phys.10 4079

[8]ShuMan E S,Barry J F,G lenn D R,DeMille D 2009 Phys.Rev.Lett.103 223001

[9]ShuMan E S,Barry J F,DeMille D 2010 Nature 467 820

[10]HumMon MT,Yeo M,Stuh l B K,Collopy A L,X ia Y,Ye J 2013 Phys.Rev.Lett.110 143001

[11]Yeo M,HumMon MT,Collopy A L,Yan B,HemMerling B,Chae E,Doyle J M,Ye J 2015 Phys.Rev.Lett.114 223003

[12]Kobayashi J,A ikawa K,Oasa K,Inouye S 2014 Phys.Rev.A 89 021401

[13]Zhelyazkova V,Cou rnol A,Wall T E,MatsushiMa A,Hudson J J,Hinds E A,Tarbutt MR,Sauer B E 2014 Phys.Rev.A 89 053416

[14]Ji Z H,Zhang H S,Wu J Z,Yuan J P,Yang Y G,Zhao Y T,Ma J,Wang L R,X iao L T,Jia S T 2012 Phys.Rev.A 85 013401

[15]Isaev T A,Hoekstra S,Berger R 2010 Phys.Rev.A 82 052521

[16]Wells N,Lane I C 2011 Phys.Chem.Chem.Phys.13 19018

[17]Lane IC 2012 Phys.Chem.Chem.Phys.14 15078

[18]Kang S Y,Gao Y F,Kuang F G,Gao T,Du JG,Jiang G 2015 Phys.Rev.A 91 042511

[19]Yang R,Gao Y F,Tang B,Gao T 2015 Phys.Chem.Chem.Phys.17 1900

[20]You Y,Yang C L,Wang MS,Ma X G,Liu WW2015 Phys.Rev.A 92 032502

[21]You Y,Yang C L,Zhang Q Q,Wang MS,Ma X G,Liu WW2016 Phys.Chem.Chem.Phys.18 19838

[22]Gao Y F,Gao T 2014 Phys.Rev.A 90 052506

[23]Nguyen J H V,V iteri C R,Hohenstein E G,Sherrill C D,B roWn K R,OdoMB 2011 NeWJ.Phys.13 063023

[24]Chin C,JochiMS,Bartenstein M,A ltMeyer A,Hend l G,Ried l S,Densch lag J H,G rimMR 2004 In ternationa l Quan tuME lectronics Conference.Optical Society of AMerica:IMI3

[25]Galván A P,Zhao Y,O rozco L A,GóMez E,Lange A D,BauMer F,Sp rouse G D 2007 Phys.Lett.B 655 114

[26]López-U rrutia J R C,Beiersdorfer P,Savin D W,WidMann K 1996 Phys.Rev.Lett.77 826

[27]Werner H J,K noWles P J,K nizia G,et al.2012 Compu tat.Molec.Sci.2 242

[28]Le Roy R J 2007 LEVEL 80:A CoMpu ter PrograMfor Solving the Radial Schrödinger Equation for Bound and Quasibound Levels(University of Waterloo CheMical Physics Research Report CP-663)

[29]Zou WL,Liu WJ 2005 J.CoMput.Chem.26 106

[30]Vogelius IS,Madsen L B,D reWsen M2004 Phys.Rev.A 70 053412

[31]RaMsay D A,Sarre P J 1982 J.Chem.Soc.Faraday Trans.2 78 1331

[32]K lein R,RosMus P,Werner H J 1982 J.Chem.Phys.77 3559

[33]Huber K P,Herzberg G 2013 Molecu lar Spectra and Mo lecu lar Structure:IV Constan ts of D iatoMic Molecu les(Sp ringer Science&Business Med ia)pp90–91[34]D i Rosa MD 2004 Eur.Phys.J.D 31 395

PACS:31.15.A–,31.15.aj,37.10.MnDOI:10.7498/aps.66.163101

*Pro ject supported by the National Natu ral Science Foundation of China(G rant Nos.11504256,U 1610117,61675120),the Open Fund of Key Laboratory of T iMe and Frequency PriMary Standards and the Scientifi c,China,the State K ey Laboratory of Precision Spectroscopy,China,Technological Innovation PrograMsof Higher Education Institu tions in Shanxi,China(G rant No.2015166),Jincheng’s PrograMs for Science and Technology(G rant No.1201501004-22),the OIT PrograMof Shanxi Province,China and the Project of Shanxi Scholarship Council of China(G rant No.2016-096).

†Corresponding author.E-Mail:clli@tyust.edu.cn

‡Corresponding au thor.E-Mail:guoMiao jun85@sina.com

Theoretical investigation of laser cooling for BD+cation by ab in ito calcu lation∗

Li Ya-Chao1)Meng Teng-Fei2)Li Chuan-Liang1)†Qiu Xuan-Bing1)He Xiao-Hu1)
Yang Wen1)Guo Miao-Jun1)‡Lai Yun-Zhong1)Wei Ji-Lin1)Zhao Yan-Ting2)

1)(School of App lied Science,Taiyuan University of Science and Technology,Taiyuan 030024,China)
2)(State Key Laboratory ofQuantuMOptics and QuantuMOptics Devices,Institute of Laser Spectroscopy,Shanxi University,Taiyuan 030006,China)

18 Ap ril 2017;revised Manuscrip t

13 June 2017)

Based on consistent basis set aug-cc-pV 5Z,five low-lying potential energy curves and transition dipole MoMents X2Σ+,A2Π,B2Σ+,a4Π and b4Σ+of BD+are calcu lated by using internally contracted multi-reference con figuration interaction app roach.According to the calcu lation resu lts,ro-vibrational levels of theses electronic states are derived through solving the radial Schrödinger equation ro-vibrational equation,and then the Molecular paraMeters,Franck-Condon factors(FCFs)and radiation life are obtained by fi tting and calculations.The FCFs(f00=0.923)and radiation life for υ′′=0(τ=235 ns)of A2Π–X2Σ+are suitable for achieving rapid laser cooling.Therefore,an optical-cycle for Dopp ler laser cooling scheMe is p roposed:the systeMincludes the A2Π1/2(υ′=0)–X2Σ+(υ′′=0,1),where the case ofυ′=0 contains 2 rotational levels,the cases ofυ′′=0 and υ′′=1 contain 6 and 4 rotational levels,respectively.According to the p roposal,we simulate the dynaMic p rocess of theMolecular popu lation in laser cooling.The BD+can be decelerated froMinitial velocity of 100 m/s to 4.6 m/s(13 MK)after scattering 1150 photons during 5.4 Ms.

BD+cation,MRCI,spectroscopic parameters,Doppler laser cooling

10.7498/aps.66.163101

∗国家自然科学基金(批准号:11504256,U 1610117,61675120)、中国科学院时间频率基准重点实验室开放基金、精密光谱科学与技术国家重点实验室开放课题、山西省高等学校科技创新项目(批准号:2015166)、晋城市科技攻关项目(批准号:1201501004-22)、山西省高等学校创新人才支持计划和山西省回国留学人员科研资助项目(批准号:2016-096)资助的课题.

†通信作者.E-Mail:clli@tyust.edu.cn

‡通信作者.E-Mail:guoMiao jun85@sina.com

©2017中国物理学会C h inese P hysica l Society

http://Wu lixb.iphy.ac.cn