基于图像信息熵的p tychography轴向距离误差校正∗

窦健泰 高志山 马骏†袁操今 杨忠明

1)(南京理工大学电子工程与光电技术学院,南京 210094)

2)(南京师范大学物理科学与技术学院,南京 210097)

基于图像信息熵的p tychography轴向距离误差校正∗

窦健泰1)高志山1)马骏1)†袁操今2)杨忠明1)

1)(南京理工大学电子工程与光电技术学院,南京 210094)

2)(南京师范大学物理科学与技术学院,南京 210097)

(2017年2月26日收到;2017年6月1日收到修改稿)

ptychography,轴向距离误差,图像信息熵

1 引 言

相干衍射成像(coherent diff raction imaging,CDI)是一种使用迭代算法直接从测量的衍射图案中获得物体的相位的成像技术,其成像分辨率不受光学元件质量的限制,理论上可达到衍射极限[1−4].在X射线和电子束等短波长成像领域中,CDI弥补了高性能光学元件的缺乏对成像质量的影响.但由于其成像视场和收敛速度等方面存在明显不足,传统的CDI技术在实际应用中受到较大限制.为解决成像视场和收敛速度的问题,2004年,谢菲尔德大学的Rodenburg等[5−7]以及文献[8—10]提出了ptychography的方法,该方法是通过物体和照明光之间的相对移动,并在远场探测器表面形成一组衍射斑,将这些衍射斑记录后,相邻的移动位置的衍射斑具有重叠部分,重叠部分的信息有助于相位恢复和加快收敛,进而可准确地重建出被测物体的振幅和相位信息.与CDI相比,ptychography具有收敛快、视场大、可靠性高等优点,目前已应用在可见光、X射线和电子束成像领域[11−14].

Ptychography在应用中要求照明场的空间分布函数已知,但现实中照明场函数很难精确测量.Maiden和Rodenburg[15]改进了ptychography算法,提出了扩展的ptychography算法,其可同时重建照明场和样品的复振幅信息.在扫描过程中,由于扫描平台的扫描精度和漂移等不确定性,严重限制了ptychography的精度和分辨率.为校正扫描误差,提出了共轭梯度算法[16]、遗传算法[17]、退火方法[18]、全局漂移模型[19]、互相关技术[20]和pcFPM等[21]算法.这些方法虽然可精确校正扫描误差,但同时增加了处理时间.为了抑制扫描误差以及减少计算时间,文献[22—24]提出了通过改变二维扫描方式以及取消扫描方式实现对扫描误差的校正的方法.在上述提到的迭代方法中,物体和电荷耦合器件(charge coup led device,CCD)或互补金属氧化物半导体(comp lementary metal oxide seMiconductor,CMOS)之间的轴向距离是参与整个计算过程的,所以轴向距离误差会影响最终的重建结果.在实际测量轴向距离时,由于CCD或CMOS保护玻璃的存在,实测的轴向距离不是有效轴向距离,所以很难精确测量物到光强记录面的轴向距离,轴向距离误差会使重现的图像模糊,并降低其分辨率.

为校正ptcychography算法中的轴向距离误差,本文提出了一种基于图像信息熵的轴向误差校正方法,该方法不仅适用于有常规扫描的p tychography算法,也适用了各种改进的p tychography算法.本文基于菲涅耳积分理论,建立了一个轴向距离误差模型,指出轴向距离误差会使重构图像具有弥散性像差,导致图像模糊.当轴向距离误差过大时会严重影响重构图像的清晰度,进而降低图像的分辨率.根据轴向距离误差对重构图像的清晰度的影响,在迭代过程中使用图像信息熵可确定图像最清晰时对应的轴向距离,从而实现校正轴向距离误差.

2 理 论

2.1 轴向距离误差理论模型

在迭代的ptychography算法中,照明场P(x0,y0)与物体O(x0,y0)在物平面上相作用,即物平面出射波前U0(x0,y0)=P(x0,y0)*O(x0,y0),将U0(x0,y0)由衍射理论传输到记录平面得到U(x,y).在记录平面上做强度限制,即将记录平面实际采集到的衍射斑强度替换U(x,y)的强度,然后逆向传输回物平面,再经ptychography的算法更新相应的物函数O(x0,y0)和照明场函数P(x0,y0),详细的ptychography算法见参考文献[11—15,22—24].物平面到记录平面的距离即为轴向距离,其参与了整个迭代过程,若其误差较大则会影响最终的重建图像.为分析轴向距离误差对复原结果的影响,本文根据菲涅耳衍射理论建立了轴向距离误差模型,当轴向距离为α2-d,α为延展因子,d是实际的轴向距离,记录平面的复振幅U(x,y)可由菲涅耳衍射理论推导如下:

U(x,y)

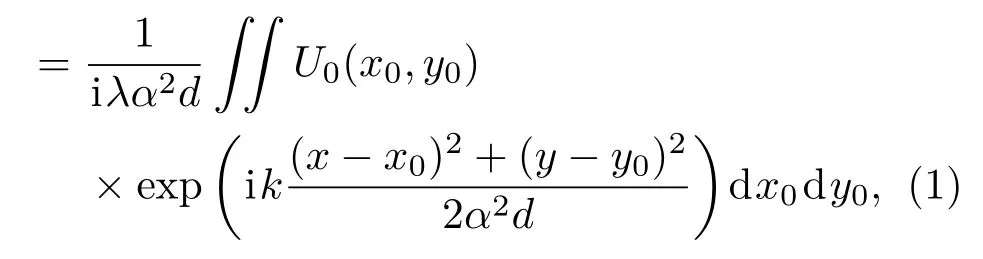
其中(x0,y0)和(x,y)分别表示物平面和记录平面的坐标;k=2π/λ,λ是工作波长.

记录平面在实际轴向距离接收的复振幅Ua(x,y)的菲涅耳衍射公式的表达如下:

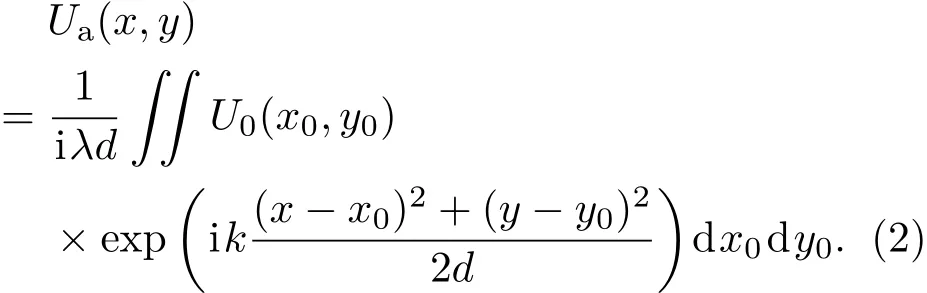
当U(x,y)传输到记录平面,需用实际采集的强度信息替换U(x,y)的强度,所以在重建图像时,(1)和(2)式的模应相等,所以将(1)式进行坐标变换,变换结果如下:

但是，俄罗斯源于政府缺乏稳定社会基础的政治危机并未随之消逝，其表征为权力的转移并非极权体制向民主政治的转轨，而是彰显出精英转换的色调。面对这种不容乐观的态势，对导致政党政治在国家政治生活实践中的实际重要性降低的制度进行调治厘革，是使成长中的俄罗斯民主得以发展并巩固的有效途径，唯有如此才能完善俄罗斯的政党政治制度。

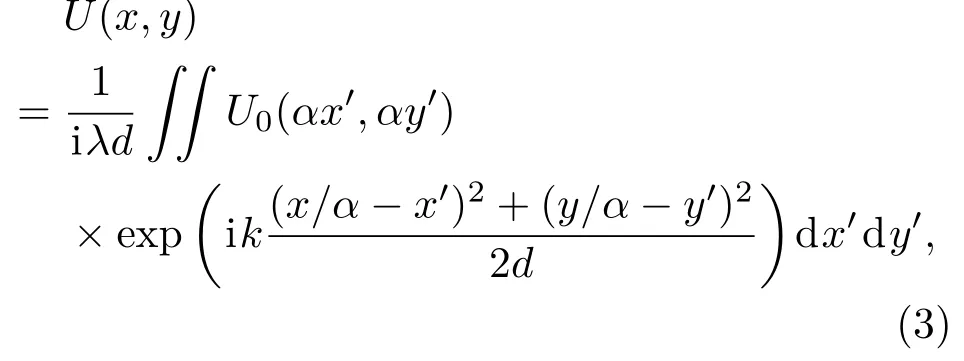
其 中x′= x0/α,y′= y0/α,U0(αx′,αy′)=P(αx′,αy′)*O(αx′,αy′), 此时物平面坐标系由(x0,y0)转化成(x′,y′). 当轴向误差存在时,重建的图像会产生弥散性像差,从而使图像模糊.当轴向误差不同时,对重建像的影响不同,造成图像的模糊程度也不同.

2.2 基于图像信息熵的轴向距离误差校正算法

图像清晰度评价函数是图像的自动调焦技术的核心[25−27],基于图像的自动调焦过程是清晰度评价函数对不同位置图像清晰程度的评价过程,当评价函数值达到峰值时,此时图像最清晰,对应的位置即被认定为聚焦位置.为保证定位精度,理想的清晰度评价函数应具有无偏性、单峰性、灵敏度高等特性.基于上述的轴向距离误差理论模型,我们可认为在轴向距离参与迭代的ptychography算法中,校正轴向距离误差的过程和自动调焦的过程相同.如(5)式所示,本文将图像信息熵[28],作为图像清晰度评价函数引入到迭代过程中,在迭代过程中不断修复距离,直到寻找到评价函数的峰值才停止,此时将最终的轴向距离继续代入迭代循环,重构出清晰的图像.

在迭代次数m＜Mt或收敛判断函数C(m)＜T时,迭代的ptychograph算法始终将粗测初始轴向距离代入,其中Mt和T分别为阈值,当大于Mt或小于T时,我们认为迭代过程处于收敛情况,即重构图像的灰度值变化不再明显.当迭代达到收敛时,引入轴向距离校正函数dc(n)和图像信息熵f(dc).

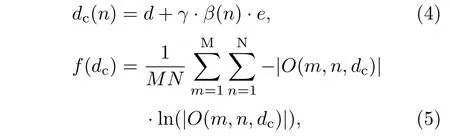
其中d是初始的粗测轴向距离.β(n)可以是常数,也可以是关于n的函数,该函数可放大或缩小校正程度e,从而控制校正轴向误差的速度.γ表示为搜索方向,γ=1为正向搜索即增加轴向距离,反之,γ=−1为逆向搜索即减少轴向距离,γ的详细表达式如(6)式所示.n是在校正轴向误差循环中的迭代次数,即n=m−Mt(m＞Mt).|O(dc)|是在轴向距离为dc的物平面上的重构像的模,M和N是|O(dc)|的元素总数.

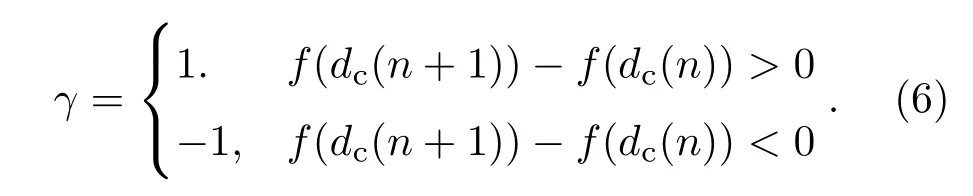
图像信息熵f(dc)是计算在轴向距离dc时物平面上重建图像的强度清晰度,f(dc)具有无偏性、单峰性、灵敏度高等特点.f(dc)的梯度变化可反映搜索理想轴向距离的方向,如(6)式中γ所示,当f(dc(n+1))−f(dc(n))＞0,搜索方向为正向即增加代入的轴向距离,反之,减少代入轴向距离的值.当f(dc)满足(7)式时,图像信息熵到达峰值,即图像最清晰的位置,校正轴向距离误差函数dc(n)停止更新,并将f(dc(n))对应的轴向距离代入迭代中,直至达到收敛条件停止(C(m)＜Tc,Tc＜T).

在本文中选用了图像信息熵作为图像清晰度评价函数,并与图像能量变化和Tamura系数比较[27,28],如(8)和(9)式所示.

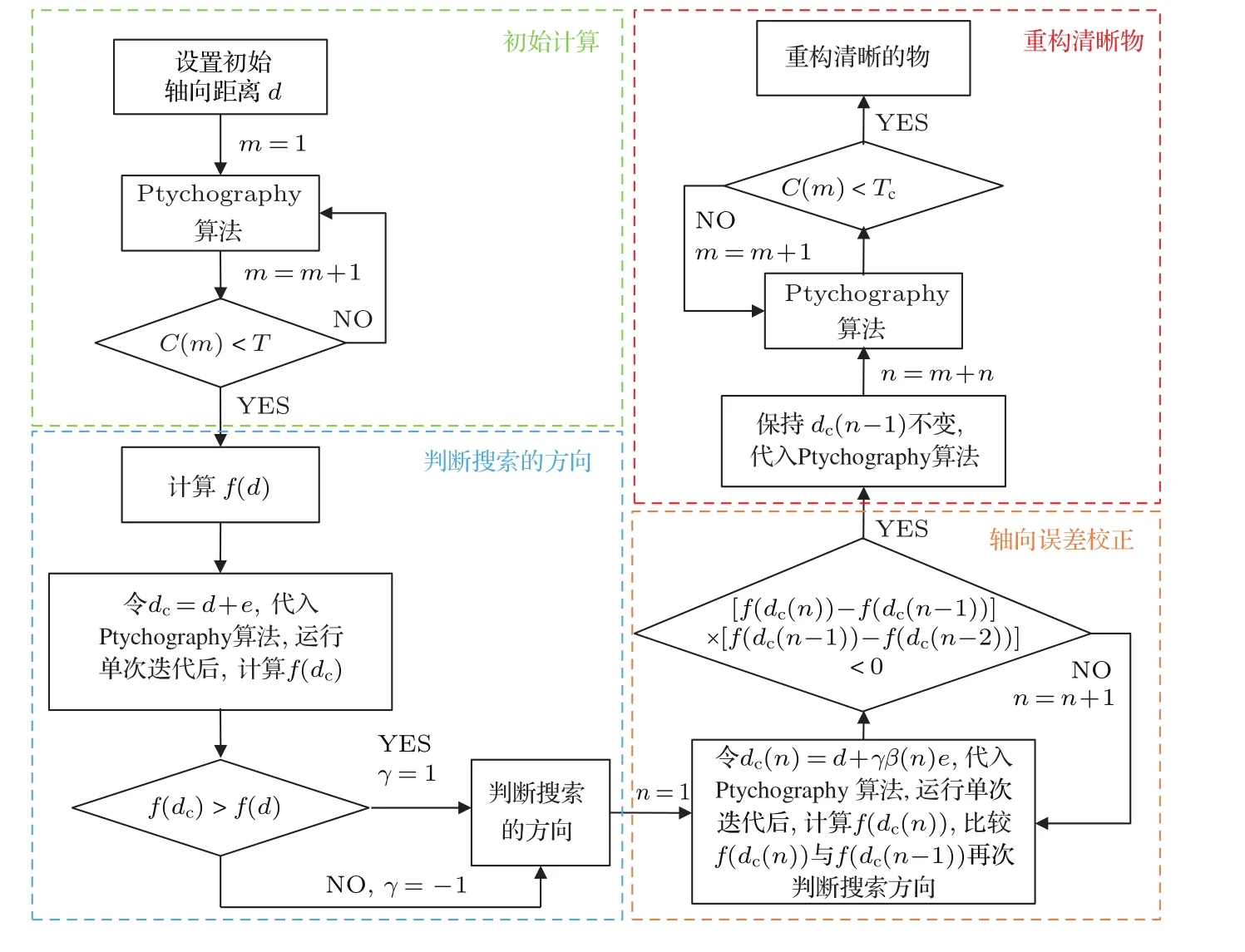
图1 (网刊彩色)校正轴向距离误差算法流程图Fig.1.(color on line)FloWd iagraMof the axial distance error correction algorithm.

其中|O(dc)|是在轴向距离为dc的物平面上的重构像的模,σ(.)是计算矩阵标准差的函数,〈.〉是计算矩阵平均值的函数,M和N是|O(dc)|的元素总数.

图1描述了基于图像信息熵的轴向距离误差校正算法的流程,该流程共包含四个部分:初始计算、判断搜索的方向、轴向误差校正以及重构清晰物.初始计算部分是确保在进入其他部分时,随着迭代的进行,重构物的复振幅信息趋于稳定,这样可保证图像信息熵在校正轴向误差时的精确度.判断搜索方向部分是确定初始的轴向距离是大于实际轴向距离或小于实际轴向离.轴向误差校正部分是寻找图像清晰度分布曲线的峰值,峰值对应图像最清晰时的位置.当峰值位置确定后,轴向距离取峰值对应的值,保持该轴向距离不变代入算法,进入重构清晰物部分,从而实现消除轴向距离误差获取清晰物的目的.

3 仿 真

为验证本文提出方法的正确性,我们设计了仿真计算,该仿真选用了如下系统参数:工作波长λ=632.8 nm,CCD具有1024×1024像素,每个像素尺寸是4.4µm×4.4µm.选用了常规的扫描式ptychography算法作为主体程序,照明光阑的直径是200个像素,扫描的步长是80个像素,共扫描了4×4个位置.待测物体到CCD的实际轴向距离是75mm.

3.1 轴向距离误差对复原结果的影响

由于CCD或CMOS到物平面的距离很难精确测量,代入迭代循环计算中的轴向距离存在误差,如果误差过大会使重现的图像模糊,并引起图像分辨率降低.本节分析轴向距离误差对复原结果的影响,并引入均方差(mean square error,MSE)作为轴向距离误差对重构结果影响的评定.

其中O(m,n)和OR(m,n)是被测物体和重构物体的振幅或相位,M和N是参与计算的矩阵元素数目.

图2给出了不同轴向距离时的重构结果以及关于轴向距离误差的MSE.图2(a)是在理想轴向距离下的复原结果,其轴向距离d=75 mm;图2(b)是在轴向距离d=74.99 mm下的复原结果,其存在轴向距离误差∆d=−0.01 mm;图2(c)是在轴向距离d=74.8 mm下的复原结果,其存在轴向距离误差∆d=−0.2 mm.比较图2(a)和图2(b)中红色矩形框中可发现轴向距离误差∆d=−0.01 mm时对重构结果的清晰度影响可忽略不计,对分辨率的影响也可忽略不计.而轴向距离误差∆d=−0.2 mm对重构结果的影响很严重,尤其是红色矩形框中,线对和数字已经变得模糊,严重影响了重构图像的分辨率.为分析轴向距离误差对复原结果的影响,选取归一化灰度值的Lena图像作为被测物体的振幅和相位,图2(d)描述了不同轴向距离误差对Lena重构结果的MSE的影响,可发现当轴向距离误差绝对值小于0.01 mm,MSE的变化很小,可认为在此范围内轴向距离误差对重构结果无影响.

3.2 图像清晰度在迭代过程中的变化规律

在ptychography算法中,随着迭代,重构物体的强度信息趋于稳定,增加迭代次数的强度信息变化微乎其微,此时引入图形清晰度受迭代次数的影响较小.本节讨论图像能量变化、Tamura系数和图像信息熵这三种图像清晰度评价函数在重构物收敛后的迭代过程中的变化规律,根据图像清晰度评价函数的单峰性确定峰值位置,即图像最清晰位置,此位置对应的轴向距离即为实际测量时的轴向距离.图3给出了初始轴向距离为d=74 mm和d=75.9 mm时的图像清晰度分布曲线,理想轴向距离为d=75 mm.为方便比较不同图像清晰度在相同情况下的分布情况,在迭代次数m＞100之后,我们设置β(n)=n,校正程度e=0.1 mm,对图3(a),γ=1,而在图3(b)中γ= −1.从图3中,可发现归一化的图像能量变化、Tamura系数和图像信息熵都具有单峰性,且峰值位置相同,该位置对应的轴向距离为d=75 mm,与理想轴向距离相同,说明图像清晰度可用于确定轴向距离.比较图像能量变化、Tamura系数和图像信息熵的清晰度分布,可发现图像信息熵相比于其他两个具有更高的灵敏性,所以本文选用图像信息熵作为校正轴向距离误差所用的图像清晰度评价函数.

图2 (网刊彩色)轴向距离误差对复原结果的影响 (a)理想距离下复原结果;(b)在轴向距离误差为−0.01 mm的复原结果;(c)在轴向距离误差为−0.2 mm的复原结果;(d)关于轴向距离误差的MSEFig.2.(color online)Eff ect of axial distance error on the retrieved iMage:(a)Retrieved iMage With the actual axial distance;(b)retrieved iMage With the axial d istance error−0.01 mm;(c)retrieved iMage With the axial d istance error−0.2 mm;(d)MSE based on the axial distance error.

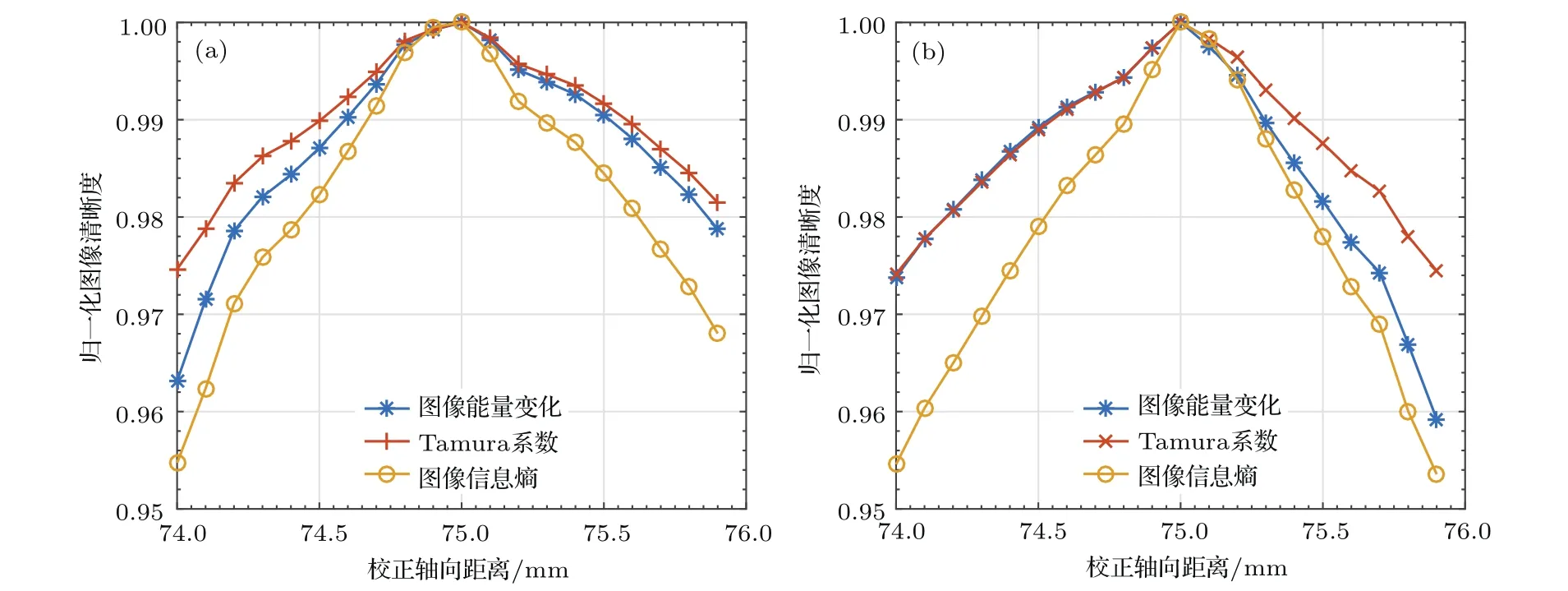
图3 (网刊彩色)关于轴向距离的图像清晰度 (a)初始轴向距离d=74 mm;(b)初始轴向距离d=75.9 mmFig.3.(color on line)IMage sharpness based on axial d istance:(a)Initial axial d istance d=74 mm;(b)initial axial d istance d=75.9 mm.

3.3 校正轴向误差前后仿真结果比较

图4 (网刊彩色)仿真结果比较 (a)理想距离下复原结果;(b)轴向距离d=74.5 mm;(c)关于轴向距离的图像清晰度;(d)校正轴向距离后复原结果Fig.4.(color on line)CoMparisons of siMu lation resu lts:(a)Retrieved resu lt With ideal axial d istance;(b)retrieved resu lt With axial distance d=74.5 mm;(c)iMage sharpness based on axial d istance;(d)retrieved resu lt With corrected ideal axial d istance.

现仿真轴向距离误差校正的过程,仍选择分辨率版作为待测物体. 理想的轴向距离是d=75 mm,实际代入迭代过程的轴向距离是d=74.5 mm.图4(a)是在理想轴向距离下重构的结果,图4(b)是在轴向距离d=74.5mm时重构的结果,可发现轴向距离误差存在时,重构像变得模糊,很难分辨原始图像中的数字和线对.在迭代次数M＞ 100之后,我们设置β(n)=n、γ=1、校正程度e=0.005mm进行搜索图像最清晰时的位置.图4(c)给出了归一化的图像能量变化、Tamura系数和图像信息熵在搜索图形清晰度峰值时的变化曲线,可发现本文采用的三种图像清晰度评价函数峰值均处于d=75 mm位置,证明了图像清晰度可用于确定轴向距离.图4(c)也指出图像信息熵相比其他另外两种图像清晰度评价函数具有更高的灵敏性.当搜索到图像清晰度的峰值后,保留峰值所处的轴向距离,并代入迭代的ptychography程序中,继续更新物函数直至满足下一次的收敛情况.图4(d)是最终的复原结果,线对和数字都变清楚,与理想情况下的复原结果非常接近.该仿真结果证明了本文提出的基于图像清晰度评价函数的ptychography轴向距离误差校正的方法是正确的.

4 实 验

基于仿真的结果,搭建了一套用于验证本文提出轴向距离误差校正方法的ptychography系统,实验的具体结构如图5所示.激光光源采用波长为632.8 nm的He-Ne激光器.激光光束经扩束准直后成平面波,再依次通过可变的小孔光阑到达样品表面,最后由CCD采集衍射图样.CCD选用的是8 bit,1600×1200个像素,像素尺寸是(4.4×4.4)µm2.X-Y方向的扫描平台是选用ThorlabsMTS50-Z8,在本实验中的扫描步长是0.2mm,孔径光阑的直径是1mm.

图5 (网刊彩色)实验系统结构Fig.5.(color on line)Structure of the experiMental system.

在实际实验中,由于CCD窗口深度的问题很难精确测量物体到CCD靶面的轴向距离,将测量得到的距离代入迭代循环中必然会引入轴向距离误差,导致重构结构的分辨率降低.如图5的实验系统中,初始测量的轴向距离d=100 mm,将初始距离代入p tychography算法中,图6(a)展示了在d=100 mm时的复原结果,重构的物体很模糊,说明初始的轴向距离与真实的轴向距离相差甚远.图6(b)是经轴向距离误差校正后(d=107.83mm)的复原结果,与图6(a)相比,重构物具有更清晰的边缘轮廓信息.

图6 (网刊彩色)实验结果 (a)初始轴向距离d=100 mm时复原结果;(b)轴向距离误差校正后复原结果Fig.6.(color on line)ExperiMental resu lts:(a)Retrieved resu lts With initial axial d istance d=100 mm;(b)retrieved resu ltsWith axial distance error correction.

5 结 论

在被测物体与CCD轴向距离参与运算的ptychography算法中,由于CCD窗口深度的问题,轴向距离误差无法避免,而过大的轴向距离误差会严重影响重构结果的清晰度和分辨率.本文提出了一种基于图像信息熵的ptychography轴向距离误差校正的方法,该方法是在算法满足收敛条件后,引入轴向距离校正函数,同时计算每个轴向距离下的图像清晰度.根据图像信息熵的单峰性,可确定图像最清晰时对应的轴向距离,保留此轴向距离继续代入ptychography算法当再次满足收敛条件后,便可重构出清晰的物体,达到校正轴向距离误差的目的.图像信息熵具有单峰性,峰值位置对应图像最清晰时的轴向距离,图像信息熵相比于图像能量变化以及Tamura系数具有更高的灵敏性,更适合于校正轴向距离误差.通过模拟仿真以及实验均证实了本文提出的方法可用于校正轴向距离误差.本文提出的轴向距离误差校正方法不仅适用于ptychography算法,也适用于其他轴向距离参与迭代运算的相位复原算法.

[1]Shen C,Tan J,WeiC,Liu Z 2016Opt.Express 24 16520

[2]H irose M,ShiMoMura K,SuzukiA,Burdet N,Takahashi Y 2016 Opt.Express 24 11917

[3]K iMC,K iMY,Song C 2016 J.Phys.:Condens.Matter 28 493001

[4]H ruszkeWycz S O,Cha W,And rich P,Anderson C P,U lvestad A,Harder R,HereMans F J 2017 APL Mater.5 026105

[5]Rodenbu rg JM,Fau lkner H ML 2004 Appl.Phys.Lett.85 4795

[6]Rodenburg J M,Hurst A C,Cullis A G 2007 U ltraMicroscopy 107 227

[7]Maiden A M,Rodenbu rg JM,HuMph ry MJ 2010 Opt.Lett.35 2585

[8]Bunk O,Dierolf M,Kynde S 2008 U ltraMicroscopy 108 481

[9]Wang Y L,Shi Y S,Li T,Gao Q K,X iao J,Zhang S G 2013 Acta Phys.Sin.62 234201(in Chinese)[王雅丽,史祎诗,李拓,高乾坤,肖俊,张三国2013物理学报62 234201]

[10]Wang H Y,Liu C,Pan X C 2014 Chin.Opt.Lett.12 010501

[11]Wang B S,Gao SM,Wang J C 2013 Acta Opt.Sin.33 0611001(in Chinese)[王宝升,高淑梅,王继成 2012光学学报33 0611001]

[12]Liu C,Walther T,Rodenburg JM2009 U ltraMicroscopy 109 1263

[13]He X L,Liu C,Wang J C 2014 Acta Phys.Sin.63 034208(in Chinese)[何小亮,刘诚,王继成2014物理学报63 034208]

[14]Rodenburg JM2008 Adv.IMag.E lect.Phys.150 87

[15]Maiden A M,Rodenburg JM2009 U ltraMicroscopy 109 1256

[16]Guizar-Sicairos M,Fienup J R 2008 Opt.Express.16 7264

[17]Shen field A,Rodenbu rg J M2011 Appl.Phys.109 124510

[18]Maiden A M,HuMphry MJ,Sarahan MC,K raus B,Rodenbu rg J M2012 U ltraMicroscopy 120 64

[19]Beckers M,Senkbeil T,Gorniak T,G iewekeMeyer K,Sald itt T,Rosenhahn A 2013 U ltraMicroscopy 126 44

[20]Zhang F C,Peterson I,V ila-CoMaMala J,D iaz A,Berenguer F,Bean R,Chen B,Menzel A K,Robinson I,Rodenburg J M2013 Opt.Express 21 13592

[21]Sun J S,Chen Q,Zhang Y Z,Zuo C 2016 Opt.Express 7 1336

[22]ShiMobabAt,Kakue T,Okada N,Endo Y,HirayaMa R,HiyaMa D,Ito T 2014 Opt.ComMun.331 189

[23]Liu C,Pan X C,Zhu J Q 2013 Acta Phys.Sin.62 184204(in Chinese)[刘诚,潘兴臣,朱健强2013物理学报62 184204]

[24]Wang H Y,Liu C,Pan X C,Cheng J,Zhu J Q 2014 Chin.Opt.Lett 12 010501

[25]Wang Y W,Liu X L,X ie H 2006 Opt.Precis.Engineer.14 1063(in Chinese)[王义文,刘献礼,谢晖 2006光学精密工程14 1063]

[26]Zhang L X,Sun H Y,Guo H C 2013 Acta Photon.Sin.42 605(in Chinese)[张来线,孙华燕,郭惠超2013光子学报42 605]

[27]Zhu Z T,Li S F,Chen H P 2004 Opt.Precis.Engineer.12 537(in Chinese)[朱铮涛,黎绍发,陈华平2004光学精密工程12 537]

[28]MemMolo P,D istante C,Patu rzo M,Finizio A,Ferraro P,Javidi B 2011 Opt.Lett.2011 36 1945

PACS:42.30.Rx,42.30.–d,42.40.–i,42.30.KqDOI:10.7498/aps.66.164203

*Project supported by the National Natural Science Foundation of China(G rant Nos.61575095,61377015,61505080)and Young E lite Scientist Sponsorship PrograMby Chinese Association for Science and Technology(G rant No.2015QNRC 001).

†Corresponding author.E-Mail:Majun@n just.edu.cn

Correction of ax ial d istance error in p tychography based on iMage in forMation entropy∗

Dou Jian-Tai1)Gao Zhi-Shan1)Ma Jun1)†Yuan Cao-Jin2)Yang Zhong-Ming1)
1)(School of Electronic and Optical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)
2)(DepartMent of Physics,Nanjing NorMal University,Nanjing 210097,China)

26 February 2017;revised Manuscrip t

1 June 2017)

Ptychography p rovides an extreMely robust and highly convergent algorithMto reconstruct the speciMen phase With a Wide field of view.The resolution and accuracy of ptychography are severely restricted by the uncertainty of the position error that includes the scanning position and axial distance error.In fact,it is diffi cult to accurately Measure the distance between the target p lane and entrance pupil of charge-coup led device(CCD)or coMp leMentary metal oxide seMiconductor,which results in the axial distance error.The axial distance error can b lur the reconstructed iMage,degrade the reconstruction quality and reduce the resolution.In order to analyze the eff ect of the axial distance error,the Model for axial distance error is derived based on the aMp litude constraint in CCD and Fresnel diff raction integral.Thismodel indicates that the axial distance error can cause a stretching deformation of the retrieved image,which is siMilar to the defocusing eff ect caused by diff erent axial distances in holography.In this paper,we propose a method of correcting the axial distance error by using the image in formation entropy in an iterative way to obtain the accurate axial distance and retrieve the distinct iMage.The correction Method based on the iMage inforMation entropy is coMposed of four parts:the initial calculation,the deterMination of the direction search,the axial error correction and the reconstruction of the distinct image.The initial calculation part is to ensure that the intensity of the reconstructed ob ject tends to be stable before entering into the other p rocessing parts.The search direction portion is to indicate that the initial axial distance is greater than the actual axial distance,or less than the actual axial distance.The axial error correction section is to calculate the sharpness values of the image at diff erent axial distance,and find the peak position of the sharpness distribution that corresponds to the position of the clearest iMage.The axial distance can be taken froMthe peak position.The obtained axial distance is again taken into account in the ptychography algorithMto eliMinate the axial distance error and obtain the distinct reconstructed image.In this paper,some simu lations are conducted to verify the feasibility of the proposed Method.The eff ect of the axial distance error is analyzed.The image energy variation,the Tamura coeffi cient and the image in formation entropy are selected as the image definition evaluation functions in our paper.We coMpare the distributions of three image definition evaluation functions in the correction process of the axial distance error.It is found that the iMage in forMation entropy has higher sensitivity than the other image definition evaluation functions.Finally,both simulation and experiment have p roved the feasibility of axial distance error correction based on iMage inforMation entropy.

ptychography,axial distance error,image information entropy

10.7498/aps.66.164203

∗国家自然科学基金(批准号:61575095,61377015,61505080)和中国科协“青年人才托举工程”(批准号:2015QNRC001)资助的课题.

†通信作者.E-Mail:Majun@n just.edu.cn

©2017中国物理学会C h inese P hysica l Society

http://Wu lixb.iphy.ac.cn