水平成层土坡破坏机理及稳定性分析

王志斌，姚亮



水平成层土坡破坏机理及稳定性分析

王志斌1, 2，姚亮1

(1. 湖南科技大学土木工程学院，湖南湘潭，411201；2. 湖南科技大学岩土工程稳定控制与健康监测省重点实验室，湖南湘潭，411201)

采用室内模型试验及极限分析上限法对水平成层土坡破坏机理与稳定性进行研究。首先，构建室内模型分别模拟不同边坡高度与不同分层厚度条件下的水平成层土质边坡，分析在坡顶条形荷载作用下坡顶与坡面位移−荷载变化规律、极限承载力及破坏面形态和位置。基于极限分析上限法基本原理，针对水平成层土质边坡圆弧+直线的破坏模式建立机动容许速度场，推导该类边坡在坡顶条形荷载作用下极限承载力的求解公式，并将室内试验结果与数值分析结果进行对比分析。研究结果表明：水平成层土质边坡在坡顶条形荷载作用下的破坏模式为圆弧+直线组合式，其滑动面由凹向边坡体内部的圆弧曲面和平面2部分组成，圆弧曲面上端位于加载梁后缘处，下端处于填土分层处，平面为填土分层交界面；上限法在求解水平成层土质边坡稳定性问题上具有一定的合理性。

水平成层土坡；破坏机理；稳定性；模型试验；极限分析上限法；滑动面

水平成层土质边坡在自然界广泛存在，既有人工开挖的边坡(如基坑、路堑等)，也有人工填筑的路堤边坡等，对其稳定性进行评价是进行边坡支护设计和填方路堤设计的重要环节。边坡变形破坏机理是边坡灾害预报和防治的理论基础。对破坏机理进行研究，不仅能够揭示边坡的破坏过程，同时对边坡的稳定性评价、滑坡预报、滑坡防治等方面也有重要的作用[1]。众多研究者通过理论分析[2]、试验研究[3−7]等对其进行了分析，其研究对象包括土质边坡、石质边坡。在边坡稳定性计算方法方面，常见解法主要有极限平衡法、极限分析法、数值分析法和滑移线法等。极限分析上限法是一种利用虚功原理分析结构物稳定性的近似解法[8−10]，只要设计出合理的、满足速度边界条件和不可压缩条件的运动学许可速度场就能求出变形力的上限解，比有限元法和滑移线法等更容易求解[10]，因此，得到了广泛应用。国内外学者通过采用此方法分别对岩质斜坡地基上填方路堤[3−4]、平面滑动型岩质边坡的稳定性[11]、双层地基极限承载力[12]、块裂层状岩质边坡[13−16]等稳定性进行分析[17−18]，验证了其较好的适用性。尽管人们对边坡破坏机理与稳定性进行了计算，但对水平成层土质边坡的研究较少，在现行公路路基设计规范[15]和土力学研究中，多将其视为均质体，或仅考虑其分层土层的物理特性，但忽略层间接触面的影响，这在一定程度上掩盖了水平分层土体材料内部应力和应变的本质特性，也将导致应力与应变的计算结果与真实结果相差较大。因此，针对水平分层土质边坡的破坏机理进行研究具有重要的实际意义。为此，本文作者采用室内模型试验的方法，对不同边坡高度、不同分层厚度的水平成层土质边坡破坏机理进行研究，并运用极限分析上限法基本原理，由室内模型试验得出水平成层土质边坡滑动面，建立机动容许速度场，以期获得其极限承载力的上限解，为相关类型工程提供参考。

1 室内模型试验

采用室内模型试验模拟水平成层土质边坡在坡顶条形荷载作用下的变形性状，分析其塑性区的发生及发展规律，进而得出其破坏机理。

1.1 试验土样

室内模型试验采用的土样为黏性土，模型试验前通过常规试验得到土体的一些基本参数如表1所示。

1.2 试验方案

本次试验共进行5组，模型尺寸如图1所示，其宽度为100 cm。其中，方案A-1，A-2和A-3边坡模型填筑高度均为80 cm，分层厚度分别为20.0，16.0和26.7 cm，通过该组试验得出不同的分层厚度对其破坏机理的影响。方案A-1，B-1和B-2边坡模型分层厚度均为20 cm，填筑高度分别为80，100和60 cm，通过该组试验得出不同的边坡高度对其破坏机理的影响。考虑最大限度的利用试验模型箱，5组边坡模型试验的设计坡率均采用1:1，而没有考虑边坡坡率这个影响因素。

模型试验在自制的模型箱内进行。试验槽长为1.55 m，宽为1.00 m，挡板高为1.05 m。为减小边界摩擦力的影响，在模型箱四周涂刷油漆。采用20 t千斤顶和箱体上部焊接反力梁提供荷载，利用试验室内长×宽×高为0.60 m×0.25 m×0.15 m的矩形梁作为加载板，对应的采用20 t压力传感器来控制加载力，采用量程为50 mm的百分表测量坡顶沉降和坡面 位移。

1.3 试验步骤

每组模型试验的步骤为：土样拌合→模型填筑→压实度检测→加载测量设备安装→加载控制→数据观测记录→模型开挖。

1.4 试验过程

考虑到水分蒸发的损失，试验土样按照略大于最佳含水率1%~2%进行掺水拌合，待土样与水充分融合后按照每组试验方案的要求进行分层填筑，每层一次性填筑压实至预定标高，借助木模形成坡面。每层填筑完成后均测定压实度，经测试土层压实度均达到90%以上。

当边坡模型填筑到设计标高后，检查坡顶平整度，满足要求后安装加载装置，同时安装百分表。百分表沿坡面布置2列，分别用于观测坡面竖向位移和水平位移，土体分层处设置测点。图2所示为A-1方案百分表布置图，其余方案类似。

表1 土样物理力学参数

注：填土抗剪强度指标采用固结排水三轴试验获得，层间接触面抗剪强度指标采用直剪试验获取。

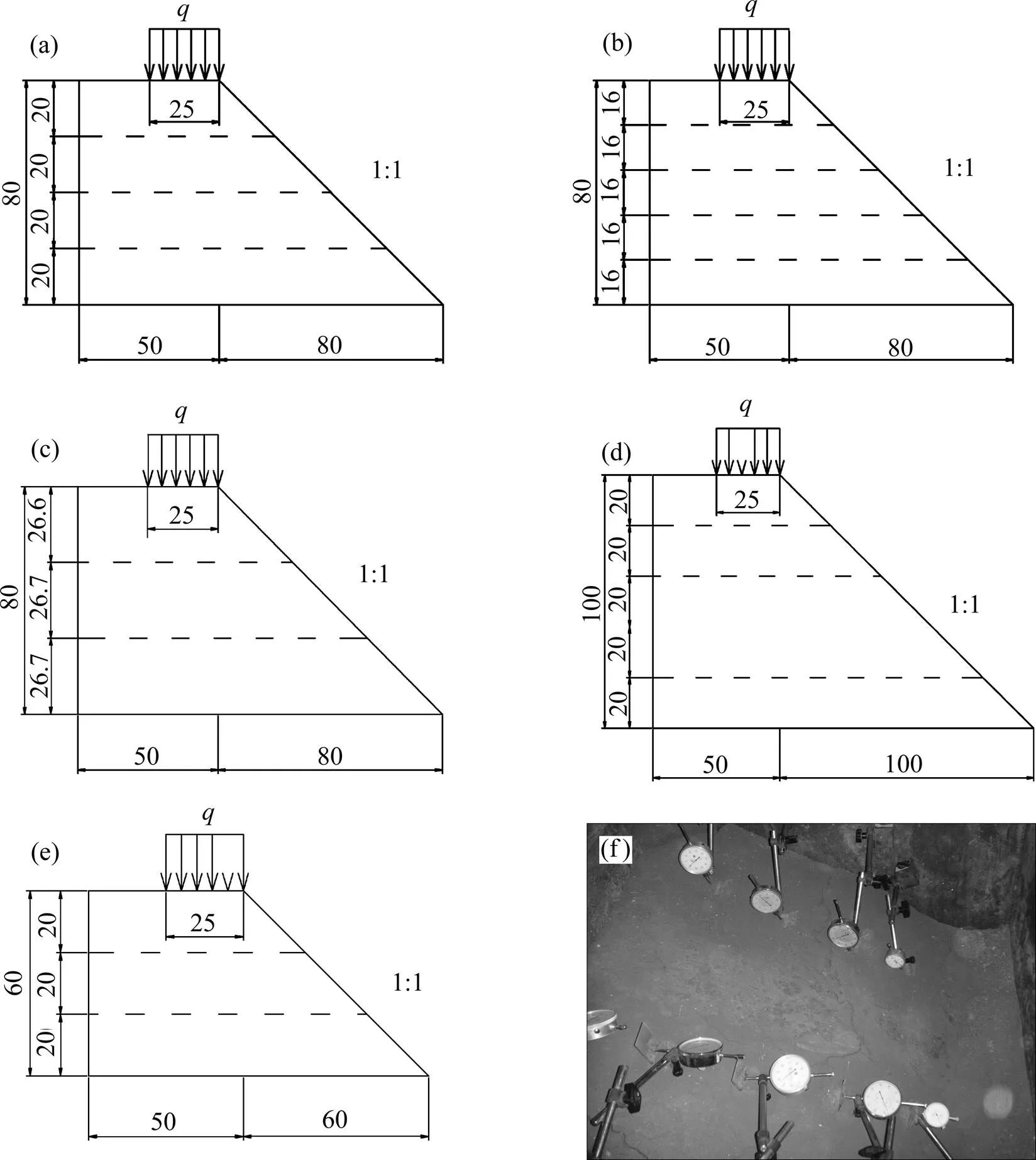
方案：(a) A-1；(b) A-2；(c) A-3；(d) B-1；(e) B-2；(f) 现场模型试验照片

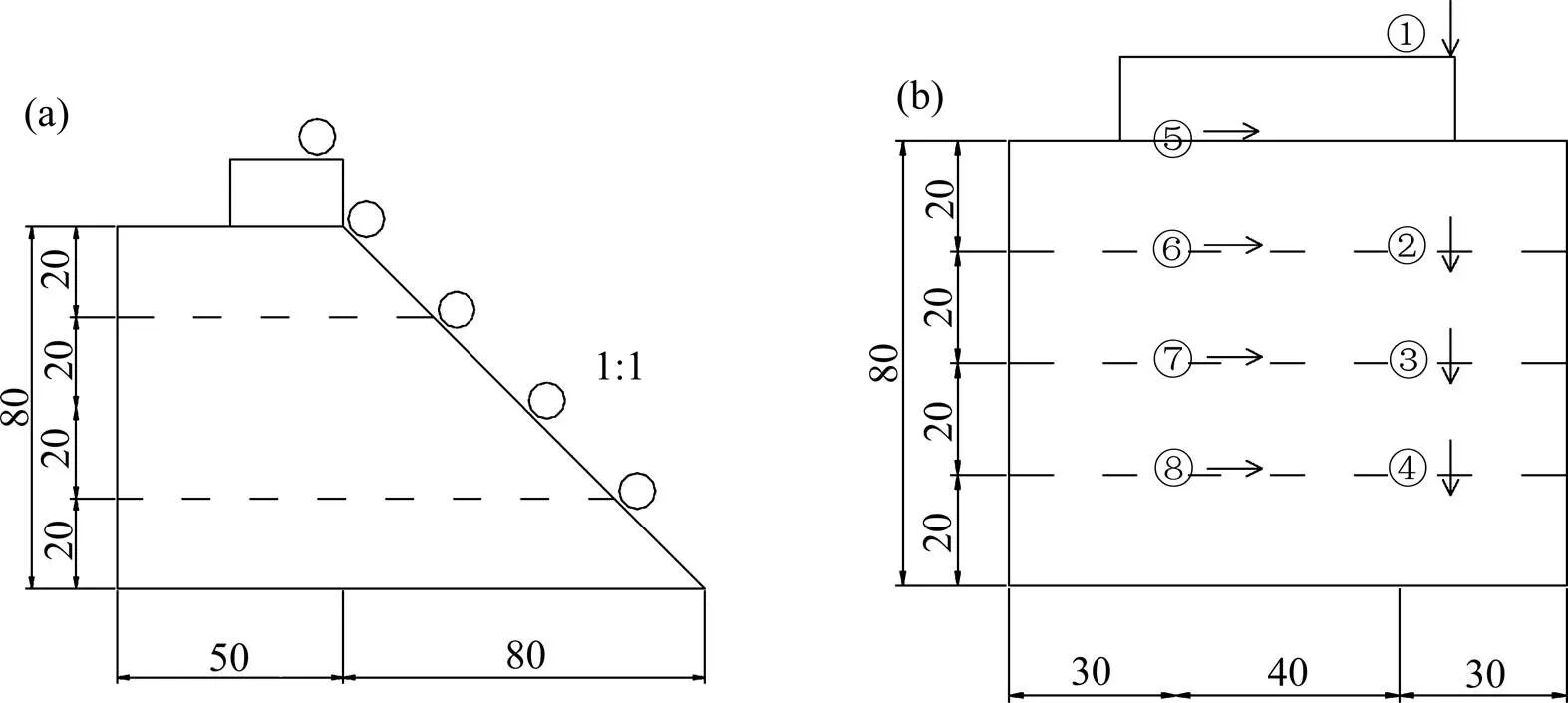
(a) 断面图；(b) 平面布置图

模型填筑、测试装置安装完成后将模型静置2 d，使模型完成先期沉降，达到初始应力平衡。

加载前测定各仪器的初始读数，荷载等级为初期5 kN(约33 kPa)，破坏期1 kN(约为7 kPa)。每级荷载维持15~30 min，然后进行下一级加载，直至模型出现比较明显裂缝为止，然后降低加载等级，并加密观测。加载直至模型不能继续承载为止。

模型失稳破坏后，拆除加载测试装置，将模型对半开挖，观测模型破坏面形态。

2 试验结果

待5组模型试验完成后，将试验结果整理，得到相关荷载­­−位移曲线、滑动面形态。

2.1 位移特征

2.1.1 坡顶沉降

5组试验方案坡顶位移随顶面荷载的变化曲线如图3所示。从图3可以看出：坡顶沉降随着顶面荷载增加，先后经历了3个阶段，即压密变形阶段、局部剪切阶段和整体破坏阶段，这3个阶段存在2个界限荷载。以方案A-1为例，坡顶沉降在0~194 kPa荷载作用下属于压密阶段，当荷载小于此界限荷载时，边坡土体均未达到极限平衡状态，应力应变近似呈线性；当加载到194~382 kPa区段时，边坡土体处于局部剪切阶段；当荷载增至382 kPa以上时，坡顶沉降随荷载急剧增加，同时伴随坡体大范围开裂破坏，千斤顶已不能继续加载，边坡模型失稳破坏，此荷载所对应的上一级荷载(340 kPa)即为A-1边坡模型的极限承载力。

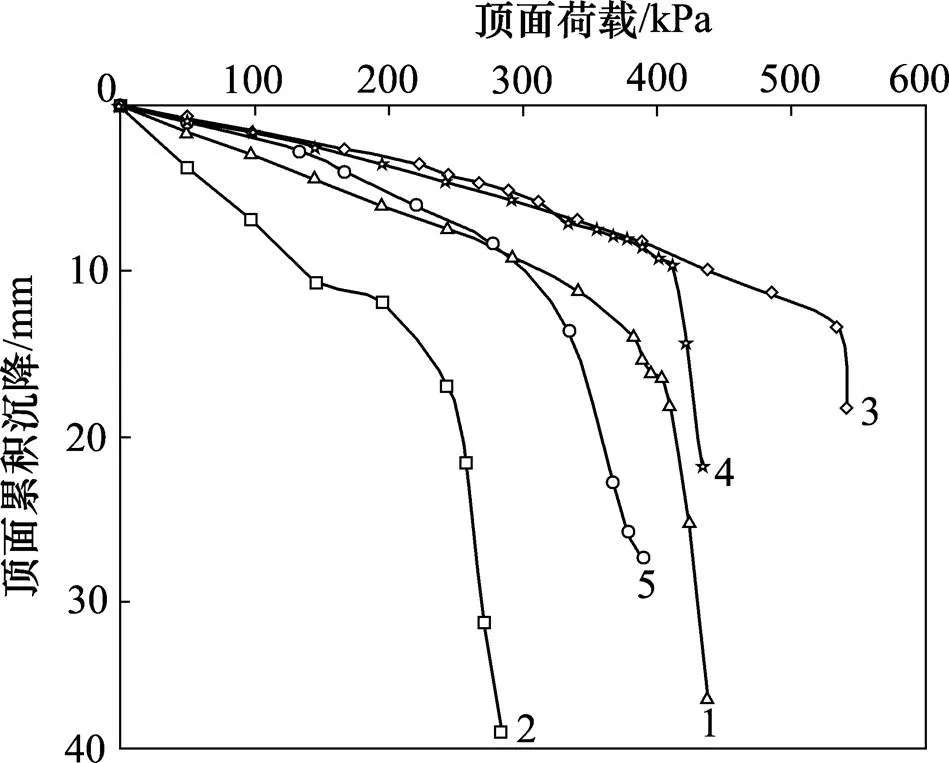
方案：1—A-1；2—A-2；3—A-3；4—B-1；5—B-2。

对模型试验加载过程中边坡外观进行观测发现：在压密变形阶段，坡顶及坡面均未见明显裂缝；局部剪切阶段首先在加载梁边缘处有细小裂缝产生，其次随荷载增大，坡面明显可见水平向裂缝发育；在整体破坏阶段，坡顶及坡面裂缝急剧增大并大范围开裂。

图3表明：在坡顶相同的条形荷载作用下，水平成层土质边坡分层厚度越大，其极限承载力越高，反之，极限承载力越低；而当坡率、加载方式及分层厚度相同时，坡体高度对极限承载力的影响不明显。

2.1.2 坡面位移

坡面位移观测内容主要分为坡面沉降和坡面水平位移。通过比较发现，5组试验方案坡面位移变化规律大体相同，这里仅以方案A-1进行说明。

图4(a)和(b)所示分别为方案A-1坡面沉降和坡面水平位移随顶面荷载变化曲线。

2号、3号、4号百分表分别布置于坡面，距离坡顶分别为20，40和60 cm。由图4(a)可知：2号百分表与3号百分表变法趋势基本相同，4号百分表有隆起现象出现，表明在本次试验过程中，坡顶条形荷载的影响深度为40 cm左右。

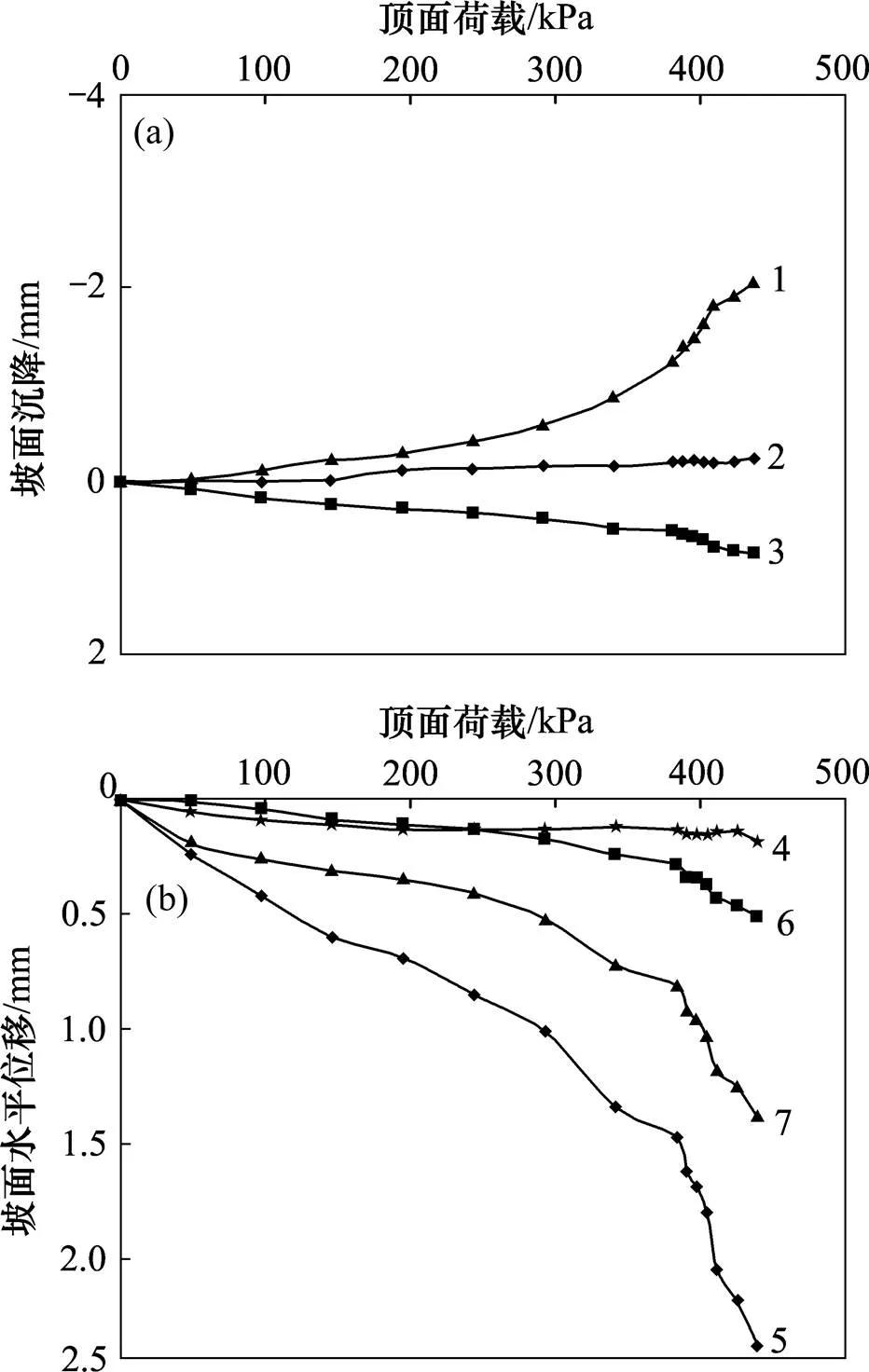
(a) 坡面沉降；(b) 坡面水平位移

6号、7号、8号及9号百分表布置于坡面，距离坡顶分别为20，40，60及80 cm。从图4(b)可见：在坡面不同位置处，各测点所测得的坡面沉降变化趋势基本相同，幅值有所区别，变化幅度依次在40，20，60和80 cm处。边坡模型破坏后显示，40 cm处正好位于滑体剪出位置。

2.2 破坏机理

试验模型在加载过程中，随顶面荷载增加，坡顶加载梁后缘处土体首先产生与之平行的一系列细微裂缝，其次后缘细小裂缝逐渐发展并贯通为1条与加载梁后缘重合的裂缝；与此同时，坡面在填土分层处出现水平向裂纹，并在该处有明显的挤出现象，边坡不能继续承载。坡体失稳后，对模型进行开挖，观察每组模型滑动面形状。开挖结果表明：各组试验模型的滑动面均可由凹向边坡体内部的圆弧曲面和平面2部分组成，圆弧曲面上端位于加载梁后缘处，下端处于填土分层处，平面为填土分层交界面，见图5。A-1模型滑动面见图6。

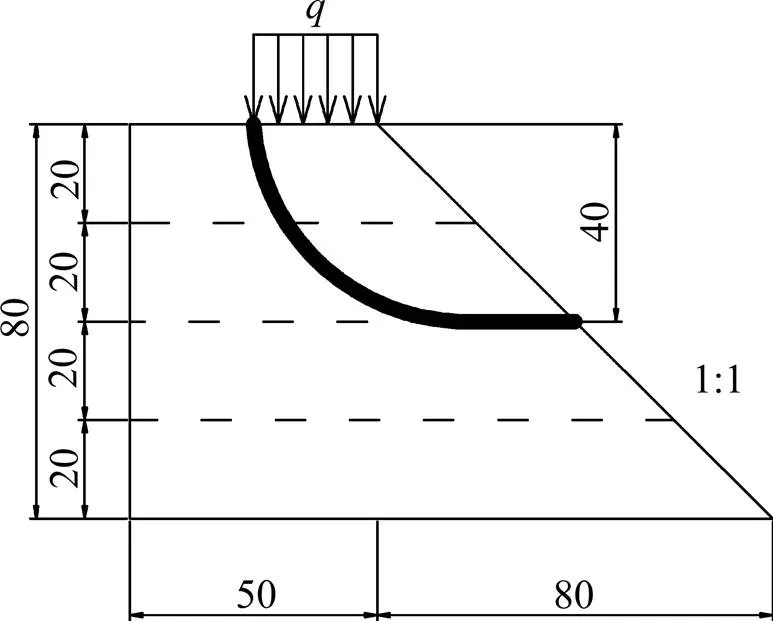
数据单位：cm

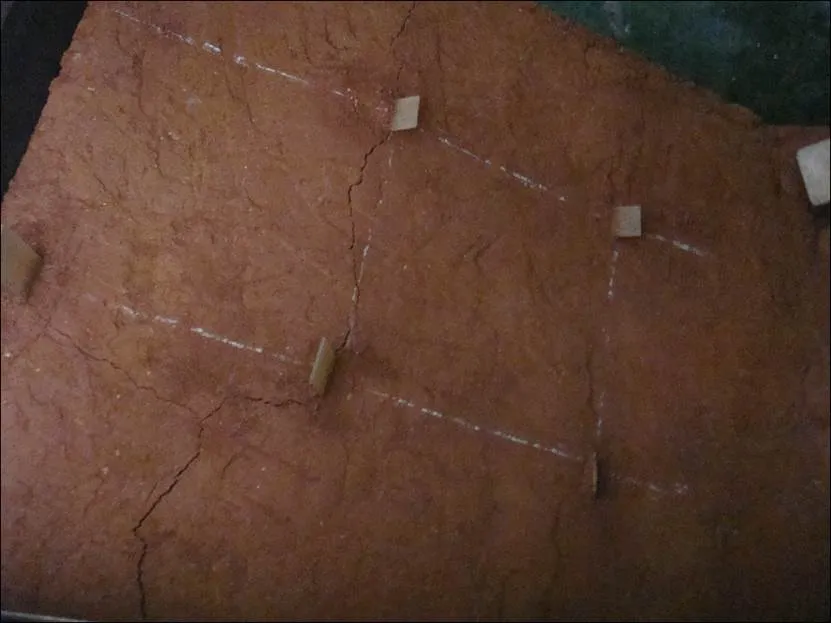
图6 A-1模型滑动面

模型A-1，A-2，A-3，B-1和B-2的滑动面剪出位置分别为40.0，32.0，26.6，40.0和40.0 cm。通过对几组模型试验进行对比分析，发现在坡率一定的情况下，坡面剪出位置主要与顶部加载方式(加载梁刚度、宽度、位置等)及分层厚度相关，A-3模型尽管剪出位置比其他模型的剪出位置高，但其滑动面的圆弧曲面曲率更大，平面段更长。

3 极限分析上限法

3.1 上限法基本原理

极限分析上限定理认为：对于任何1个有效破坏机构，假设存在1个同时满足速度边界条件和应变−速度相容条件的速度场，根据外荷载功率等于内部能量损耗率这一关系条件，能够得到1个不小于实际破坏荷载的极限荷载[9]。

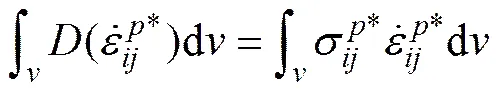
当存在速度间断面时，上限法方程可表示为

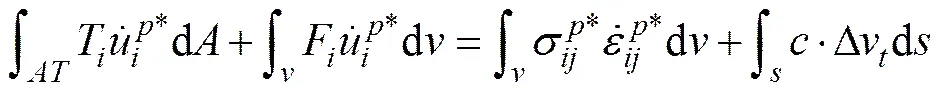
3.2 机动容许速度场

根据室内模型试验得出的破坏模式建立如图7所示的速度场，塑流被限制在速度间断线以上的区域。机构由圆弧形滑动刚块和三角形刚块组成。其中，为圆弧的圆心，为滑面绕圆心转动的角速度，为间断面上的速度，为间断面上的速度。

3.3 外功率

外力功率主要由2部分组成，即顶部荷载和土体自重所作的功率。

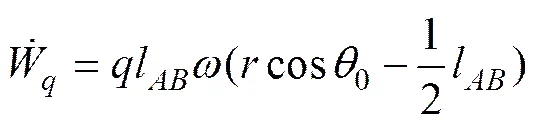
式中：为顶部外荷载(kPa)；其他符号意义如图7所示。土体自重所做的外功率用叠加法求得，分别求出，，和这4部分土体所作的功率，，和，则滑动体自重所作的外功率为

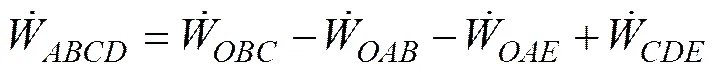
计算图如图8所示。

首先计算区域土体自重所作的外功率，取其中1个微元(如图8(a)所示)，该微元所作的外功率为

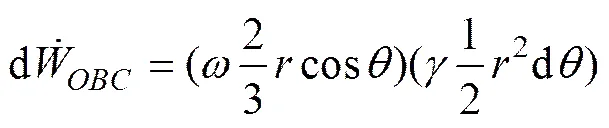
(6)

据文献[9]，圆弧受剪区的速度为

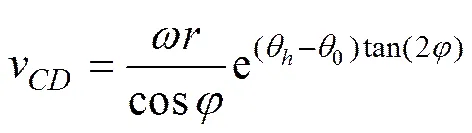
(8)

则外力和滑动区土体自重所作的功率为

李红是聪明的，之所以没有和齐海峰讲杨蓉的为人，是因为她知道，杨蓉是一个现实的人，她跟家境优渥的领导公子好上了，根本不会看上齐海峰的。

3.4 内部能量耗损率

由图8可知：内部能量耗损发生在弧和直线段上。弧面上微元的能量耗损率可由该面的黏聚力、微元弧长以及该面的切向间断速度三者的连乘积得到，因此，整个弧面的内部能量耗损率可沿整个弧面进行积分后得到：

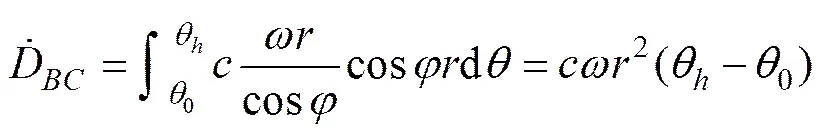
(11)

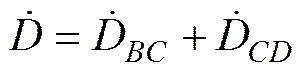
3.5 求解

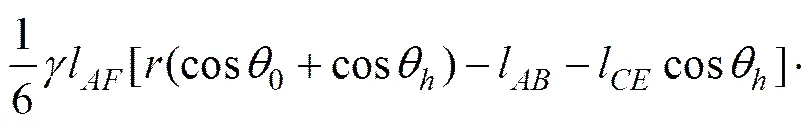
(13)

3.6 对比分析

将表1中土体物理力学参数代入式(14)，对室内试验中的5组模型工况进行求解，并将计算结果与室内试验结果进行对比，计算结果如表2所示。

从表2可以看出：上限法求得的极限承载力均比室内试验得到的结果大，最小相对误差为1.03%，最大相对误差为34.57%，这是模型试验过程中存在一些不可避免的误差所致，而且试验用土多次使用，物理性质也会发生改变。而A-2极限承载力的最大差值发生的原因主要是土体分层填筑未达到要求。因此，计算结果仍可说明上限法在该类问题的求解中具有一定的合理性。

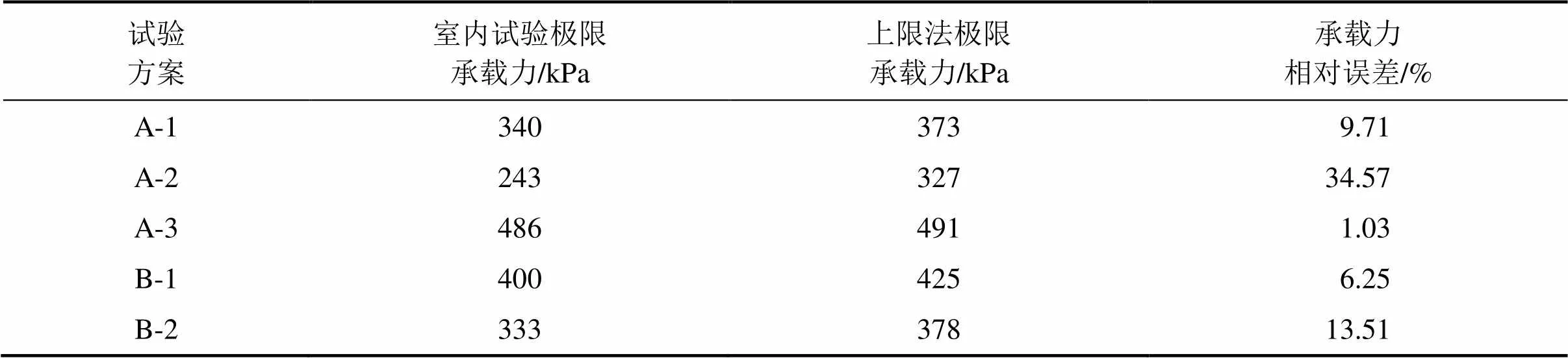
表2 极限承载力计算结果

4 结论

1) 在坡顶相同的条形荷载作用下，水平成层土质边坡分层厚度越大，其极限承载力越高，反之，极限承载力越低；而在坡率、加载方式及分层厚度相同情况下，坡体高度对极限承载力的影响不明显。

2) 在坡顶条形荷载作用下，水平成层土质边坡的滑动面由凹向边坡体内部的圆弧曲面和平面2部分组成，圆弧曲面上端位于加载梁后缘处，下端处于填土分层处，平面为填土分层交界面。

3) 对比分析室内试验和上限法得出的极限承载力，上限法计算结果均大于室内试验结果，最小相对误差为1.03%，最大相对误差为34.57%，说明上限法在求解水平成层土质边坡稳定性问题上具有一定的合理性。

[1] 倪武杰. 土质边坡破坏机理及稳定性研究[D]. 西安: 长安大学地质工程与测绘学院, 2010: 1−26. NI Wujie. Study on the failure mechanism and stability of soil slope[D]. Xi’an: Chang’an University. School of Surveying and Mapping, 2010: 1−26.

[2] TERZAGHI K. Mechanism of landslide[C]// Application of Geology to Engineering Practice (Berkey Volume). PAIGE S, ed. Washington D C: Geological Society of America, 1950: 83−123.

[3] 王志斌. 岩质斜坡地基上填方路堤稳定性研究[D]. 长沙: 中南大学土木工程学院, 2007: 20−71. WANG Zhibin. Stability analysis of fill embankments on rock slope[D]. Changsha: Central South University. School of Civil Engineering, 2007: 20−71.

[4] 王志斌. 极限分析上限法在山区斜坡地基上高填方路堤极限承载力研究中的应用[J]. 塑性工程学报, 2007, 14(2): 118−122. WANG Zhibin. Application of upper-bound theorem of limit analysis on ultimate capacity of embankments on mountain slope foundation[J]. Journal of Plasticity Engineering, 2007, 14(2): 118−122.

[5] 姜海西, 沈明荣, 程石, 等. 水下岩质边坡稳定性的模型试验研究[J]. 岩土力学, 2009, 30(7): 1993−1999. JIANG Haixi, SHEN Mingrong, CHENG Shi, et al. Model test on stability of underwater rock slopes[J]. Rock and Soil Mechanics, 2009, 30(7): 1993−1999.

[6] 谢永利, 胡晋川, 王文生. 黄土公路路堑边坡稳定性状离心模型试验[J]. 中国公路学报, 2009, 22(5): 1−7. XIE Yongli, HU Jinchuan, WANG Wensheng. Centrifugal model test for stability characteristics of highway cut slope in loess[J]. China Journal of Highway and Transport, 2009, 22(5): 1−7.

[7] 王艳巧, 刘斯宏, 杨俊杰, 等. 土工袋加固砂性土质边坡模型试验与上限解[J]. 岩石力学与工程学报, 2009, 28(增2): 4006−4013. WANG Yanqiao, LIU Sihong, YANG Junjie, et al. Model test of sandy soil slope reinforced by soilbags and upper-bound solution[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(Suppl 2): 4006−4013.

[8] DRUEKER D C, PRAGER W. Soil mechanics and plastic analysis in limit design[J]. Quarterly Journal of Applied Mathermatics, 1952, 10(2): 157−165.

[9] CHEN Wuifa, LIU Xila. Limit analysis in soil mechanics[M]. Amsterdam: Elsevier Science, 1990: 36−51.

[10] 陈惠发. 极限分析与土体塑性[M]. 北京: 人民交通出版社, 1995: 21. CHEN Wuifa. Limit analysis and soil plasticity[M]. Beijing: China Communications Press, 1995: 21.

[11] 王根龙, 伍法权, 张茂省. 平面滑动型岩质边坡稳定性极限分析上限法[J]. 工程地质学报, 2011, 19(2): 176−180. WANG Genlong, WU Faquan, ZHANG Maosheng. Method of upper bound limit analysis for plane sliding of rock slopes[J]. Journal of Engineering Geology, 2011, 19(2): 176−180.

[12] 秦会来, 黄茂松. 双层地基极限承载力的极限分析上限法[J]. 岩土工程学报, 2008, 30(4): 611−616. QIN Huilai, HUANG Maosong. Upper-bound method for calculating bearing capacity of strip footings on two-layer soils[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(4): 611−616.

[13] 郑惠峰, 陈胜宏, 吴关叶. 岩石边坡稳定的块体单元极限分析上限法[J]. 岩土力学, 2008, 29(增刊): 323−327. ZHENG Huifeng, CHEN Shenghong, WU Guanye. Upper bound limit method for stability analysis of rock slopes by block element method[J]. Rock and Soil Mechanics, 2008, 29(Suppl): 323−327.

[14] 张子新, 徐营, 黄昕. 块裂层状岩质边坡稳定性极限分析上限解[J]. 同济大学学报(自然科学版), 2010, 38(5): 656−663. ZHANG Zixin, XU Ying, HUANG Xin. Upper bound solution of limit analysis for stability of block-layered rock slope[J]. Journal of Tongji University (Natural Science), 2010, 38(5): 656−663.

[15] JTG D30—2004,JTG D30—2004, Specifications for design of highway subgrades[S].

[16] 李泽, 王均星, 张小艳. 基于刚性块体系统的岩质边坡稳定性上限法研究[J]. 岩石力学与工程学报, 2014, 33(S1): 2844−2852. LI Ze, WANG Junxing, ZHANG Xiaoyan. Research on upper bound method for stability of rock slope based on rigid blocks assemblages[J]. Chinese Journal of Rock and Engineering, 2014, 33(S1): 2844−2852.

[17] 杨峰, 郑响凑, 赵炼恒, 等. 地表超载作用下隧道失稳破坏的上限有限元分析[J]. 岩土力学, 2015, 36(S2): 695−701. YANG Feng, ZHENG Xiangcou, ZHAO Lianheng, et al. Finite element upper bound analysis of tunnel instability under surcharge loading[J]. Rock and Soil Mechanics, 2015, 36(S2): 695−701.

[18] 唐高朋, 李亮, 赵炼恒, 等. 非线性破坏准则下边坡稳定性极限分析斜条分法[J]. 岩土力学, 2015, 36(7): 2063−2072. TANG Gaopeng, LI Liang, ZHAO Lianheng, et al. Inclined slices method for limit analysis of slope stability with nonlinear failure criterion[J]. Rock and Soil Mechanics, 2015, 36(7): 2063−2072.

(编辑 陈灿华)

Analysis of stability and failure mechanism of horizontal stratified soil slope

WANG Zhibin1, 2, YAO Liang1

(1. School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China;2. Key Laboratory of Geotechnical Engineering for Stability Control and Health Monitoring, Hunan University of Science and Technology, Xiangtan 411201, China)

Model testing was conducted to study the failure mechanism of the horizontal stratified soil slopes using upper bound theory of limit analysis. The variation law among the displacement and load, ultimate bearing capacity and the shape and position of sliding surface of the horizontal stratified soil slopes were simulated with different layer thicknesses and different heights of fill under the same strip load on the upper surface of the slope. Based on the principle of upper bound theory of limit analysis, the velocity fields of the failure mode with the arc-straight line sliding surface which was obtained from model test were established. The formula was deduced for calculating the ultimate bearing capacity of slope with strip load on the top. The results show that the sliding surface consists of the circular arc surface with the inwards slope and plain surface. The top of circular arc surface is located at the back of loaded beam and bottom is in the edge of filling layers, and plain surface is the interface of filling layer. The upper bound theory of limit analysis can be used to solve the stability problem of the horizontal stratified soil slopes.

horizontal stratified soil slope; failure mechanism; stability; model test; upper bound theory of limit analysis; sliding surface

10.11817/j.issn.1672-7207.2017.07.031

TU449

A

1672−7207(2017)07−1915−08

2016−09−10；

2016−11−25

国家自然科学基金资助项目(51208523)；湖南省科技厅一般项目(2012TT2039)；贵州省交通厅科技项目(2013-122-005) (Project(51208523) supported by the National Natural Science Foundation of China; Project(2012TT2039) supported by the General Program of Department of Science and Technology of Hunan Province; Project(2013-122-005) supported by the Science and Technology Project of Communications Department of Guizhou Province)

王志斌，博士，讲师，从事路基路面工程研究；E-mail: 71496933@qq.com