基于改进比例谐振控制的三相四桥臂有源电力滤波器研究*

郑宏，张云，王哲禹，黄俊

(江苏大学电气信息工程学院，江苏镇江212013)

基于改进比例谐振控制的三相四桥臂有源电力滤波器研究*

郑宏*，张云，王哲禹，黄俊

(江苏大学电气信息工程学院，江苏镇江212013)

在有源电力滤波器电流内环控制环节，为了实现对交流量的稳态无误差跟踪，以及对主要特征次谐波和低次谐波进行充分补偿，针对谐振控制器可以无静差地跟踪交流参考量以及PI控制可以无静差地跟踪直流量的特性。采用了一种基于静止坐标系下的比例-积分-多频谐振控制策略，对含量较高的主要特征次谐波和低次谐波进行选择性补偿，有效的降低了系统的总谐波畸变率。最后，通过仿真和实验对比分析了上述控制策略的可行性。

三相四桥臂;比例-积分-多频谐振控制;三维空间矢量控制;谐波电流

在三相四线制低压供电系统中，有源电力滤波器中的三相四桥臂拓扑由于具有直流侧电压控制简单的特点成为主要的拓扑结构［1］。然而，APF的跟踪性能直接影响谐波补偿的效果。在补偿电流跟踪控制模块中，经常使用的电流控制策略有滞环控制，比例积分控制，无差拍控制等。其中滞环控制具有较快的动态响应特性并且易于实现，但是滞环控制中的宽度的选择直接关系到电力电子器件的开关频率，损耗以及达到的跟踪效果［2-3］。PI控制算法简单便于理解，但是它只能无静差地跟踪直流参量，对于交流参量的跟踪效果并不理想［4］。无差拍控制易于数字化实现，但是它的鲁棒性能比较差，因而会出现瞬态响应超调大的现象［5-6］。

在三相四线制不平衡系统中投入非线性负载时，系统的谐波电流主要以6k±1次谐波为主［7］。由于在理想的情况下谐振控制器在谐振频率处有无穷大的增益，因此可以利用它这个的特点在谐振频率处重点补偿含量较多的低次谐波来降低总的谐波畸变率。本文结合PI控制简单，实现成本低，可靠性高的优点，在此基础上并联多个谐振控制分别对5、7、11、13、17、19次低次谐波进行重点补偿，通过比例-积分-多频谐振控制降低总的谐波畸变率。

1 三相四桥臂APF的拓扑结构和控制算法

图1是并联型有源电力滤波器的系统结构，系统补偿的对象是一个非线性负载。

图1 三相四线制四桥臂主电路结构

由于Sa、Sb、Sc、Sf分别表示a、b、c、f 4个桥臂的开关状态，我们令每个桥臂上管开通、下管关断为1，反之上管关断、下管开通为0，就可以得到16个空间开关矢量，将上面的16个开关状态在静止坐标系abc下画成矢量图就可以得到一个空间的十二面体如图2所示。

图2 四桥臂逆变器在abc坐标系下的开关矢量

V1到V8在12面体上半部分，即正的区域。V9到V16在12面体的下半部分，即负的区域。这16个开关状态每个立方体的边长为1，在围成空间的十二面体中，有6个面与坐标轴平行，分别是Va=±1，Vb=±1，Vc=±1，有6个面与坐标轴呈45°角，分别是Va-Vb=±1，Vb-Vc=±1，Va-Vc=±1。因此，可以用平面Va=0、Vb=0、Vc=0和Va-Vb=0、Vb-Vc=0、Va-Vc=0将控制区域进行分割。这样控制区域可以分为24个空间四面体，并且每一个空间四面体有3个基本矢量和两个零矢量构成。确定参考矢量所在的四面体后，根据空间合成的原理，计算出3个非零开关矢量及零矢量所对应的占空比，并选择在一个开关周期插入一种零矢量［0000］，开关矢量用中心对称排序方式，从而算出各个桥臂开关作用的时间，得到控制电力电子器件开关的PWM脉冲。

2 谐振控制器的设计

有源电力滤波器采用电压外环，电流内环的双闭环控制策略。其中电流内环用来跟踪补偿电流。

2.1 传统的PI控制原理

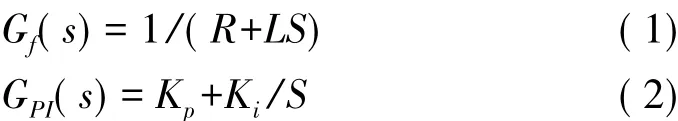
图3 PI控制原理图

PI控制虽然算法简单、实现成本低、可靠性高，而且已经被广泛的应用到自动化系统和工业控制系统中，但PI调节器对正弦参考电流很难达到理想的控制效果［8］，不能实现无静差跟踪而且不能实现对特定次谐波的完全补偿。

2.2 比例谐振控制器

当给定的参考信号是直流信号时，控制器只需要包含常规的积分器，就可以保证系统的无稳态误差，而当参考信号具有某一频率的周期信号时，就必须要采用广义积分器，结构如图4所示。

图4 常规积分器与广义积分器

对于常规积分器，当输入直流信号U时，其输出Ut，而对广义积分器，当输入为某一频率的正弦信号u(t)=U sin(ωt+φ)，其输出为y(t)=Ut sin(ωt+ φ)，这就是广义积分的无静差性;当输入信号具有偏差Δω时，即:

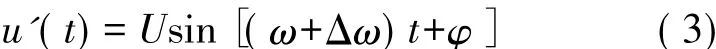
当Δω≫0时，其输出为:

在有源电力滤波器中，负载的谐波阶次通常为奇数次谐波，则:Δω=2πfB=314 rad/s或4πfB=628 rad/s，它们都满足Δω≫0的条件。

因此广义积分器具有频率选择和无静差跟踪特定次谐波的特性。谐振控制器的传递函数一般表示为:

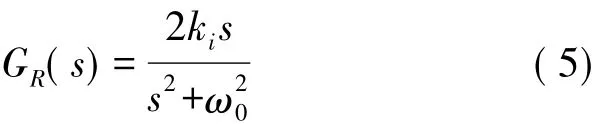
式中:ki是积分系数，ω0是谐振控制器的谐振频率。当ki=1，ω0=100πrad/s时，其幅频特性如5所示。

图5 谐振控制的幅频特性

从幅频的波特图可以看出，谐振控制器在f=50 Hz的谐振频率处增益为无穷大，并且能有效地衰减非谐振处的信号。但是由于其带宽窄，鲁棒性差，所以当电网频率波动时，不能对参考信号有效跟踪，影响控制效果，因此需要对传统的PR控制进行改进，改进的PR控制器的传递函数为:

式中:ωc是截止频率，ω0是基波谐振频率，kp是比例系数，kR为谐振系数，k是特定谐波次数。其中ω0=100π，k是要补偿的谐波次数，这两个都是已知参数，因此需要设计的就是ωc、kp和kR，为了便于分析，设其中2个参数不变，通过观察第3个参数对系统性能的影响来确定合适的值。首先设kp，kR不变，观察ωc对系统的影响，如图6所示。

图6 ωc对幅频相频特性的影响

由波特图可以看到，ωc越大，带宽也就越大，采用改进型的PR控制可以增加带宽，减弱电网频率波动对特定次谐波补偿效果的影响。根据带宽的定义，|G(jω)|=kR/对应的两个频率差即为带宽，经过计算，PR控制器的带宽为ωc/πHz。根据国家电网频率波动标准B级，容许的波动范围是+0.5 Hz～-0.5 Hz，留有一定的裕度，取波动范围为+0.7 Hz～-0.7 Hz，可得ωc/π=1.4 Hz，则ωc= 4.4 rad/s。

同理，取kR=1，ωc=4.4，不同的kp波特图如图7所示，随着kp的增大，准谐振控制器的谐振作用减少，对频率的选择性补偿也减小，容易引起谐振频率和其他频率相互干扰，对系统稳定性不好。因此kp的取值不能太大或太小，因此这里取kp=3。

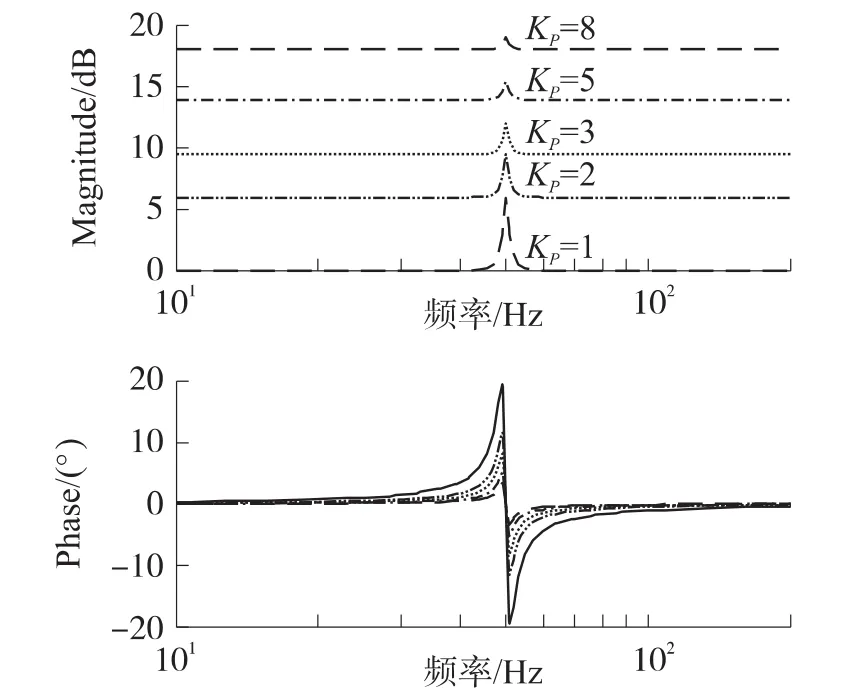
图7 kp对幅频相频特性的影响

令kp=3，ωc=4.4，改变kR的数值，就可以得到如图8所示的波特图，从图中可以看到，kR越大，在谐振处的增益也就越大，这里取kR=10来保证对特定次谐波交流量的无静差跟踪。

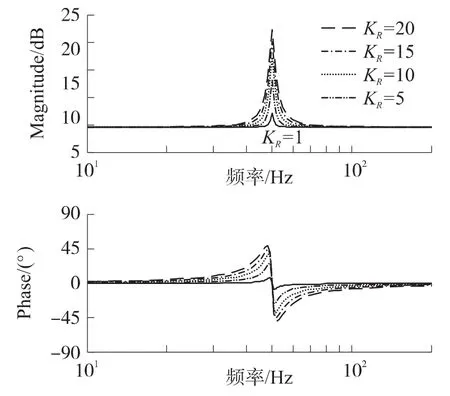
图8 kR对幅频相频特性的影响

在三相四线制系统中，投入非线性负载时，谐波主要次数是5、7、11、13、17、19等6k±1次谐波。因此本文主要对20次以下的主要谐波进行补偿，通过多个谐振控制器的并联来实现对特定次谐波的无稳态误差控制。比例-积分-多频谐振控制的原理图如图9所示。

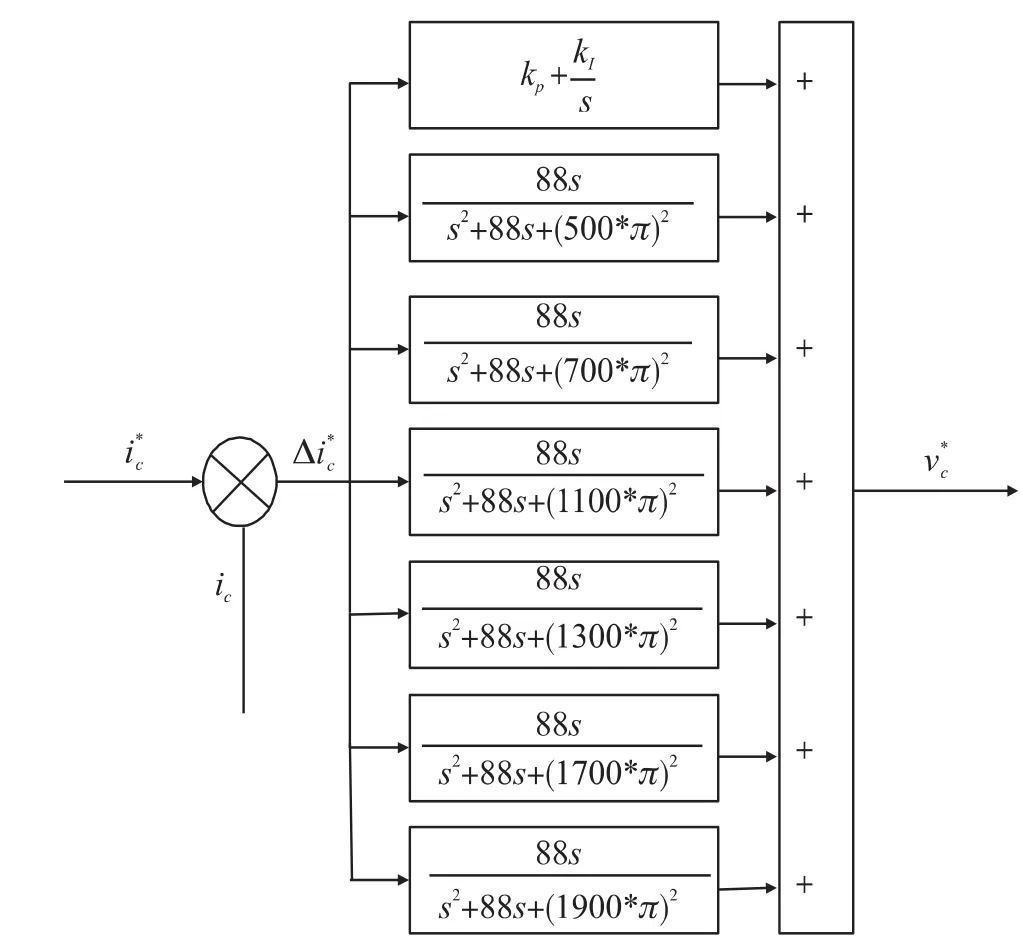
图9 准谐振控制原理图

3 比例－积分－多频谐振控制在三相四线制APF下的仿真

为了验证在静止坐标系下比例-积分-多频谐振控制正确性和有效性，这里用MATLAB里的Simulink工具搭建了三相四线制有源电力滤波器系统的仿真模型，总的系统模型如图10所示。

仿真参数的选择:交流测电压为220 V/380 V，电网电压的频率为50 Hz，主电路交流测的电感为4.22 mH，主电路直流侧电容参考电压为800 V，谐波负载为阻感负载的三相不控桥整流电路，其中R=28Ω，L=4mH，开关频率为12.8 kHz。

如图10所示，该系统模型是由电源模块，负载模块，检测模块，比例-积分-多频谐振控制模块还有APF这5个不同的子模块组成，为了验证有源电力滤波器在空间矢量调制算法下对中线的补偿能力，因此本文搭建了三相四线制不平衡系统。对于检测模块，这里我们用的是基于同步坐标变换的d-q-0检测法。有源电力滤波器模块的作用是对检测到的系统的谐波进行补偿，产生与之等值，方向相反的电流。

图10 有源电力滤波器系统的仿真模型

如图11所示，是补偿之前的三相电网电流波形，由于搭建的是三相四线制非线性不平衡系统，所以这里的a，b，c三相电流的幅值不相等，形状近似马鞍波。其中a相的电流值为50 A左右，b，c两相的电流值为28 A左右，图上中线电流呈正弦波，幅值为30 A。

图11 补偿之前的三相电网电流波形

图12是采用PI控制器补偿之后的三相电网电流波形，系统的反应时间在0.01 s之内，由于时间的限制这里总的仿真时间取到0.2 s，由图可见补偿后a，b，c三相由原来幅值不等的马鞍波变为幅值相等，为38 A左右，相角相差120°标准的正弦波，同时，中线电流也得到了很好的补偿，由原来的幅值为28 A的正弦波变为幅值很小在0上下摆动的小波。并通过FFT分析可知，A、B、C相总的谐波畸变率由原来的11.29%，26.38%，

25.92 %降低为2.54%，2.70%，2.39%，如图13所示。

图12 PI控制补偿之后的三相电网电流波形

图13 采用PI控制器进行补偿之后的ABC三相总谐波畸变率

如图14所示，是采用比例-积分-多频谐振控制补偿之后的三相电网电流波形。通过对比图14和图12可以明显发现，采用比例-积分-多频谐振控制后的三相电网波形毛刺变少，为标准正弦波，相较于PI控制更加光滑。再对比图13和图15的FFT分析，可以看到，后者ABC三相的总谐波畸变率都降到了2%以下分别为:1.66%，1.67%，1.56%。它的20次以下的谐波中，5、7、11、13、17、19相对PI控制都得了很好的补偿。

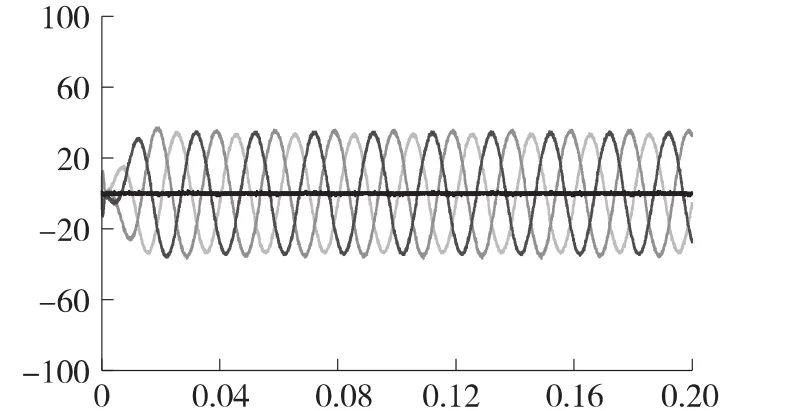
图14 采用比例－积分－多频谐振控制补偿之后的三相电网电流波形

图15 采用比例－积分－多频谐振控制

为了验证改进的比例谐振控制器的动态性能，这里在MATLAB的环境下添加Breaker器件，在0.04 s之前系统的负载是线性三相平衡负载，在0.04 s之后所带负载是三相非线性不平衡负载，有源电力滤波器在0.08 s的时候投入使用。具体的动态性能如图16所示。从图16可以看出控制器的反应时间很短，可以很快的响应并且进行滤波。

图16 比例－积分－多频谐振控制器的动态响应图

4 实验

为了进一步验证控制策略的有效性，这里搭建了三相四线制APF样机，实验平台由非线性负载，四桥臂APF主电路，四桥臂APF控制电路3部分组成。实验中的APF开关器件选择型号为FF150R17ME3G的IGBT模块，相应的驱动采用CONCEPT公司的2SP0115T2A0-17。交流侧电压为220 V/380 V，电网电压的频率为50 Hz，主电路交流测的电感为4 mH，主电路直流侧电容参考电压为800 V，开关频率为

12.8 kHz。谐波负载为阻感负载的三相不控桥整流电路，其中R=30Ω，L=4mH。

图17和图18分别是以A相为例，采用PI控制器和比例-积分-多频谐振控制器进行补偿的网侧电流的实验波形，相对PI控制而言本文提出的改进的控制器控制效果更好，A相的网侧电流更加平滑，毛刺较少，同时总谐波畸变率相对PI控制更低，在这里只补偿了20次以下的谐波。实验结果和仿真结果相一致。

图17 PI控制的实验波形

图18 比例－积分－多频谐振控制的实验波形

5 结论

本文首先简单介绍了三相四桥臂拓扑的空间矢量调制算法。针对有源电力滤波器的控制策略，考虑到谐振控制器的特点，在传统的PI控制器基础上采用了比例-积分-多频谐振控制，通过并联多个谐振控制器对含量较高的低次谐波进行重点补偿，这里文章只补偿了20次以下的5、7、11、13、17、19次谐波。最后通过MATLAB仿真软件和实验平台对采用的控制器进行了仿真和实验验证以及FFT分析，通过与PI控制器的仿真效果进行对比可以发现比例-积分-多频谐振控制的在三相四线制有源电力滤波器的补偿效果更好且具有很快的动态响应特性。这对于三相四线制低压农网具有重要的研究意义。

［1］王晓刚，谢运祥，帅定新，等.四桥臂逆变器的快速三维SVPWM算法［J］.华南理工大学学报(自然科学版)，2009，37 (7):94-99.

［2］粟时平，李圣怡.并联有源滤波器的最优电压滞环电流控制［J］.电力自动化设备，2002，22(4):14-17.

［3］李正明，唐静.基于PI控制的有源滤波器中的研究［J］.电子器件，2014，37(5):987-990.

［4］唐欣，罗安，涂春鸣.基于递推积分PI的混合型有源电力滤波器电流控制［J］.中国电机工程学报，2003，23(10):38-41.

［5］Mohammad Sedighy，Shashi BDewan，Francis PDawson.A Robust Digital Current Control Method for Active Power Filters［J］.IEEE Trans on Industry Applications，2000，36(4):1158-1164.

［6］Shin-Ichi Hamasaki，Atsuo Kawamura.Improvement of Current Regulation of Line-Current-Detection-Type Active Filter Based onDeadbeat Control［J］.IEEE Trans on Industry Applications，2003，39(2):536-541.

［7］叶梦云.基于DSP的三相四桥臂有源滤波器的研究［D］.北京交通大学，2014:4.

［8］张晓，李新宇，周睿.三相四桥臂并联型APF无差拍控制策略的研究［J］.电力系统保护与控制，2011，39(20):78-83.

郑宏(1965-)，男，汉族，教授，博士，硕士生导师，主要研究方向为大功率电力电子变换器，分布式发电;

张云(1990-)，女，汉族，硕士研究生，电气工程专业，主要研究方向为大功率电力电子变换器，有源电力滤波器，niantianhebaiyun@126.com。

Research on Improved PI-MFR Current Controller in Three Phase Four Leg APF*

ZHENG Hong*，ZHANG Yun，WANG Zheyu，HUANG Jun

(College of Electrical and Information Engineering，Jiangsu University，Zhenjiang Jiangsu 212013，China)

In three phase four wire power supply system，traditional PI control can not track dc reference volume exactly，and also can’t adequately compensate main characteristic harmonics and low order harmonics.Then，the advantage of PI controller is tracking dc referencewithout static error in a fast speed，while PR controller can track the ac reference volume errorless and fast.Combining the advantages of them both，this paper adopted a proportionalintegral-multiple frequency resonance current controller in stationary coordinates.Finally，building the whole three phase four wire system of APF.By comparison with PI controller，the proportional-integral-multiple frequency resonance current controller has a fast dynamic response and can effectively reduce the rate of total harmonic distortion.The experiment proved the correctness of the theory.

four bridge arms topology;the proportional-integral-multiple frequency resonance current controller; 3-D SVM;harmonic current

C:1270

10.3969/j.issn.1005－9490.2017.01.045

TM 713.8;TM 48

:A

:1005－9490(2017)01－0237－07

项目来源:江苏高校优势学科建设工程项目(61074019)

2015-09-24修改日期:2015-10-20