风力发电机振动采集系统的设计

褚世凯，秦会斌

(杭州电子科技大学新型电子器件与应用研究所，浙江杭州310018)

风力发电机振动采集系统的设计

褚世凯，秦会斌*

(杭州电子科技大学新型电子器件与应用研究所，浙江杭州310018)

针对振动分析在风力发电机状态检测及故障定位中的作用，设计了基于ADXL335三轴加速度传感器的振动采集系统，并通过STM32实现模数转换。对信号采集过程中出现的频率混叠，设计了六阶巴特沃斯低通滤波器，采用Savitzky-Golay平滑算法对信号中掺杂的噪声进行去噪。测试结果表明:所设计滤波器可有效滤除600 Hz以上的信号，振动加速度的误差可控制在0.5%以内;Savitzky-Golay平滑算法可有效消除信号中的噪声。

振动;风力发电机;ADXL335;巴特沃斯;Savitzky-Golay

风力发电机是风能开发的主要设备，其结构复杂，运行环境恶劣，因此风力发电机故障频发。根据实践，风力发电机常见故障主要集中在机械部件上，如齿轮箱、低速轴、高速轴以及发电机等［1］。机械振动包含的信息丰富，在故障时的反应迅速，且测量方便，因此目前风力发电机的状态检测与故障定位主要基于振动信号的分析。

赵志宏［2］等针对滚动轴承振动信号的不规则性和复杂性，提出一种基于小波包变换与样本熵的轴承故障诊断方法。郑近德［3］等针对滚动轴承不同故障振动信号具有不同复杂性的特点，提出基于多尺度熵和支持向量机的滚动轴承故障诊断方法。张淑清［4］等将局部均值分解近似熵和模糊C均值聚类方法结合，将机械振动信号局部均值分解后所得PF分量的近似熵作为特征向量，输入到模糊C均值聚类分类器中，实现了不同类型机械故障的分类识别。Bafroui［5］等将小波能谱熵应用于齿轮箱故障诊断，通过采集齿轮箱升速过程中的动态信号，并加以分析，实现了齿轮箱不同转速条件下的动态过程故障诊断。Hernandez-Vargas［6］等针对异步电机转子断条和轴承故障的早期检测问题，提出奇异值分解和信息熵相结合的方法。

现有研究主要聚焦于对振动的数字信号处理，在振动信号采集方面并没有太多的关注。但是所采集信号的准确度对后期的信号分析有着非常大的影响，对于采样过程中出现的频率混叠也只能在采集过程中进行处理。因此本文设计了风力发电机振动采集系统，采用了六阶巴特沃斯模拟低通滤波器对传感器的模拟输出进行处理，同时采用了Savitzky-Golay数据平滑算法进行信号除噪。

1 方案设计

振动采集系统的硬件结构如图1所示，利用ADXL335三轴加速度传感器采集风力发电机的振动。为了避免ADC过程中的频率混叠现象，本文有针对性的设计了低通滤波电路。通过STM32的ADC模块进行模拟信号的采集，同时STM32将采集的数据转换为加速度值。采集的数字信号通常都难以避免的掺杂着噪声［7］，如电路板之间由于器件耦合而产生的毛刺，信号采集过程中出现的周期性干扰，以及各种恶劣环境因素的影响。这些干扰噪声的频率带宽比较大，对原始信号的影响也比较严重，所以需要对信号进行平滑处理，以达到减小噪声的目的。最终将采集的数据通过串口发送给上位机。

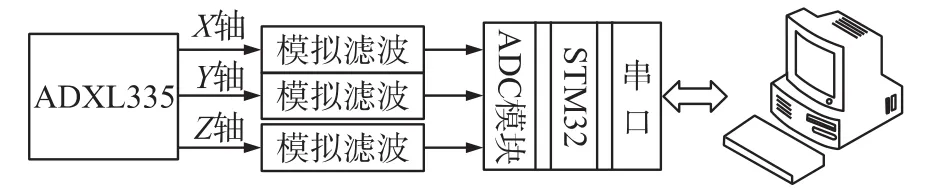
图1 系统结构图

2 ADXL335的应用

本文选取了ADXL335三轴加速度传感器，它可测量±3 gn以内的加速度，具有1.8 V～3.6 V的宽工作电压范围，可抵御10 000 gn的冲击［8］。ADXL335的灵敏度与电压成正相关，在电压为2 V时其灵敏度为195mV/gn，电压每升高0.1 V灵敏度也随之升高约10mV/gn。ADXL芯片内每个输出端都接有一个32 kΩ的电阻，如果在输出引脚上外接一个适当的电容，那就可构成简单的低通滤波电路，从而达到控制输出带宽的目的，本文中在输出引脚XOUT、YOUT、ZOUT别接0.01μF电容，使其输出带宽为600 Hz。为了减少电源中的噪声，通常会将ADXL335 VS端外接一个去耦电容，一般可采用0.1μF的电容。其应用电路如图2所示。

图2 ADXL335应用电路

3 巴特沃斯滤波器的设计

在等步长的离散采样过程中会出现混叠现象，在数学上早已通过傅里叶分析进行过证明。当发生频率混叠时，原始信号中就会夹杂原本不存在信号与频率，其直接结果就是对所采集信号造成干扰。Butterworth滤波器在其通带内幅值响应最为平坦，其阻频带的频率衰减不够出色，这方面的不足可通过增加滤波器的阶数来弥补。随着阶数的增加电路的复杂度也随之提升，因此首先需要找出满足需求的最低阶数。对此可通过式(1)进行计算:

式中，α2为最小阻带衰减，ωs为阻带频率，ωc为截止频率。本文中α2=20 dB，ωs=900 Hz，ωc=600 Hz，K=1。将参数代入式(1)可得n=5.666 480，因此巴特沃斯滤波器的阶数至少为6阶。

巴特沃斯低通滤波器的电路实现有多种，本文通过3个二阶无限增益多端反馈电路(简称MFB)的级联来实现我们所需的六阶巴特沃斯低通滤波器。二阶MFB低通滤波电路如图3所示。

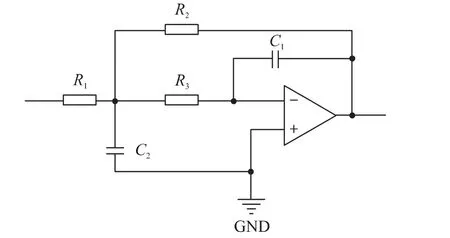
图3 二阶MFB低通滤波电路

此电路有着下面的关系式:

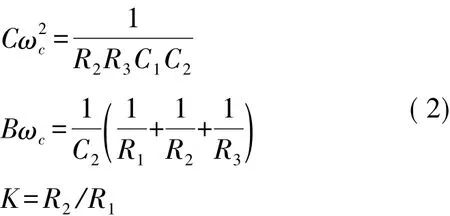
对以上各式进行整理可得:

式中，K为增益，B与C为归一化系数，对于六阶巴特沃斯滤波器，B与C的值如表1所示。

表1 六阶巴特沃斯低通滤波器的设计系数

实际中各种电阻值更容易获得，因此在设计时先设定好C1与C2的值，然后根据式(3)计算出各电阻值。在电路中如果把所有电阻乘以某个常数，同时电容除以这个常数，那么滤波器的特性不变［9］。根据这一特点可对计算出的电阻电容值进行调整。最终计算出的各电阻电容值如表2所示。因此最终设计的六阶巴特沃斯低通滤波电路如图4所示。

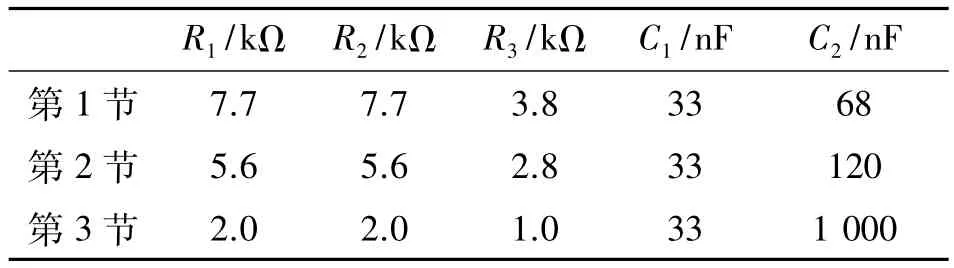
表2 计算出的电阻电容值

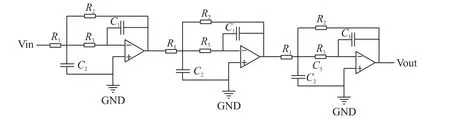
图4 六阶巴特沃斯低通滤波电路

4 数据处理

4.1 数据转换

在信号经过了低通滤波器的处理后，采用STM32f103rbt6进行模拟信号的采集。STM32f103rbt6是一款基于CortexM3内核的32 bit微处理器，其外设齐全，开发与调试都非常方便［10］。STM32f103RBT6的ADC是十二位逐次逼近型模数转换器，其最大转换速率为1 MHz。在信号采集中，一般将采样率设定为目标频率的3倍～4倍即可，本文将采样率设为3 kHz。同时本文采用DMA方式进行数据传输，大大提高了效率。对于STM32采集的数字信号，需要通过两步才能转化为加速度值。第1步是将所采集的数据转化为电压，其计算公式为:

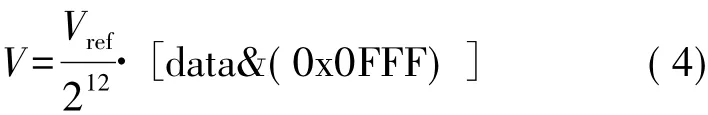
式中，1.5为传感器0 gn输出电压，φ为经过软件校准后所添加的偏移量，0.325为传感器在3.3 V电源下的灵敏度。

4.2 Savitzky-Golay平滑算法的应用

Savitzky-Golay平滑算法是在时域内利用最小二乘

式中，Vref为参考电压，本文中的参考电压为3.3 V，data为模数转换后的16 bit结果，由于是12 bit的ADC，且对齐方式为右对齐，所以我们需要先将数据的高四位清零。

第2步是将电压转化为实际的加速度值，其计算公式为:法对滑动窗口内的数据进行线性拟合的一种方法，它被广泛的运用于数据流平滑除燥［11］。相对于其他类似的平滑方法，Savitzky-Golay平滑能够消除采样信号中有较大误差的数据点，同时保留相对极大值、极小值和宽度等分布特性，尽量保证原始数据的不失真［12］。

假设有一组数据x(i)，其中i=-k，…，0，…，k，即共有2k+1个连续点。有一个n阶的多项式(如式(6))对这组数据进行拟合:

对于拟合的效果可用式(7)表示:

λ越小则说明拟合的效果越好。为了使λ最小，可令λ对各系数的导数为0，即:

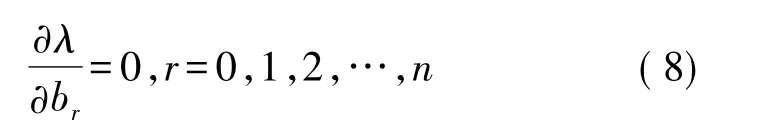
得:

式中r=0，1，…，n。对式(9)化简可得:

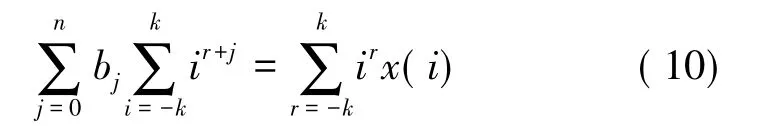
一旦确定k与n的值，再将待拟合的2k+1个数据x(i)代入上式中即可求出拟合多项式的系数。然后把中间点的横坐标输入得出的拟合多项式中，即可得到中间点在前后各k个点的基础上的最佳拟合。

5 系统测试

5.1 滤波电路幅频特性测试

在测试过程中我们将信号发生器产生的不同频率的正弦信号作为输入，用示波器观察输出信号相对输入信号的幅频变化。本实验测试了1 200 Hz以下的信号，600 Hz以下以及900 Hz以上的正弦信号每间隔40 Hz测试一次，频率在600 Hz～900 Hz之间，频率间隔20 Hz。在将得到的数据进行整理之后我们得到了实际模拟滤电路的幅频特性曲线，如图5所示。

图5 滤波电路幅频特性曲线

从图5可知，最终设计出的滤波器特性基本符合本文的设计指标。但是其通带不够平坦，且增益一直小于1，经分析这主要是由于实际电阻电容值的偏差所致。

5.2 数据精度测试

本文通过测量静态加速度的方式对数据精度进行测试，实验中让X轴、Y轴与Z轴分别垂直于地面，然后对采集的数据与标准的垂直加速度(1 gn)进行对比。在实验中由于无法将每个轴完全准确地垂直于地面，本文采用多次测量，然后去除最大值与最小值，再将数据进行平均，以达到误差的最小化。每组实验中测量次数为12次，每次测量过后将传感器重新校准。采取如上所述的方法，本文最终获得了10组数据，如表3所示。

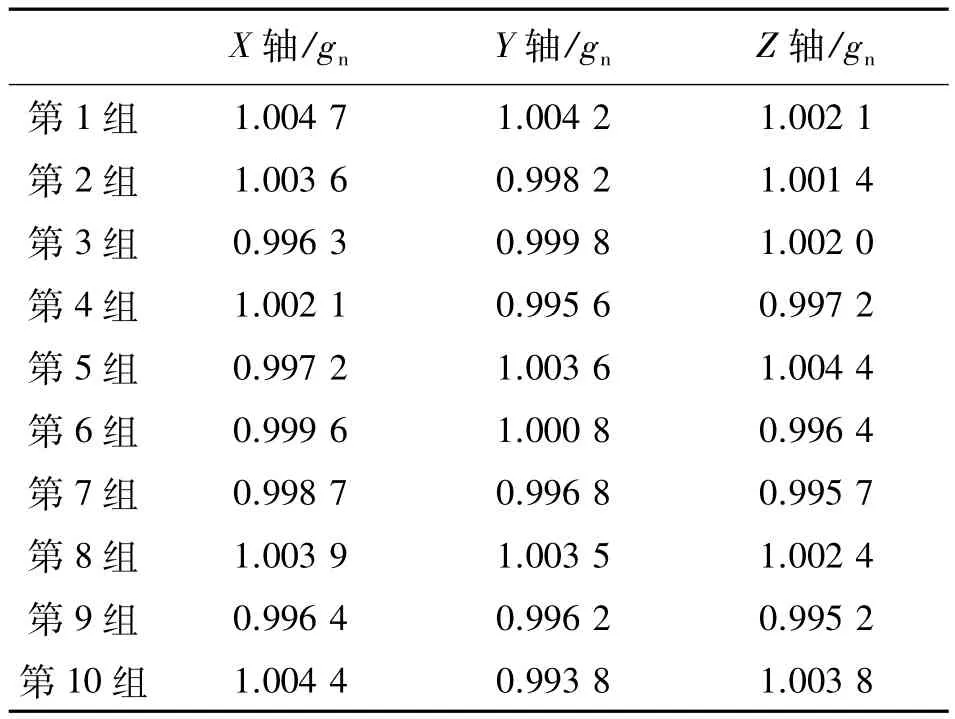
表3 数据统计结果

从表3可以看出，所采集加速度准确度较高，其中偏差最大的值为1.004 7 gn，相对标准值误差为

0.47 %。

5.3 数据平滑效果测试

Savitzky-Golay平滑算法中窗口较大可以得到更好的去噪效果，但是随着窗口的增加计算量也会增加，因此需要在二者之间进行平衡。拟合阶数较小可得到较好的去噪效果，过大则会使曲线变得毛糙。本文中窗口取15，拟合阶数取4，图6(a)为原始振动信号，图6(b)为经过Savitzky-Golay平滑的振动信号。

图6 Savitzky_Golay的振动信号

通过对比可知，Savitzky-Golay平滑算法能够消除除信号中偏差较大的点，同时保留原始信号的纹理细节。同时有研究表明，Savitzky-Golay平滑算法能够有效提高所采集数据的精度［13］。

6 结论

本文设计了基于ADXL335三轴加速度传感器的风力发电机振动采集系统，针对信号采集过程中的频率混叠以及掺杂的噪声，设计了6阶巴特沃斯低通滤电路，采用了Savitzky-Golay算法进行去噪。从测试结果来看，本设计实现了振动信号的准确采集，从而为后期的数据处理奠定了基础。

［1］娄海英.风机振动检测与监控分析系统［D］.北京交通大学，2008.

［2］赵志宏，杨绍普.基于小波包变换与样本熵的滚动轴承故障诊断［J］.振动、测试与诊断，2012(32):640-644.

［3］郑近德，程军圣，胡思宇.多尺度熵在转子故障诊断中的应用［J］.振动、测试与诊断，2013(33):294-297.

［4］Zimroz R，BartelmusW，Barszcz T，etal.Diagnosticsof Bearings in Presence of Strong Operating Conditions Non-Stationarity—A Pro-cedure of Load-Dependent Features Processing With Application Towind Turbine Bearings［J］.Mechanical Systems and Signal Processing，2014，46(1):16-27.

［5］BafrouiH H，Ohadi A.Application ofWavelet Energy and Shannon Entropy for Feature Extraction in Gearbox Fault Detection Under Varying Speed Conditions［J］.Neurocomputing，2014，133:437 -445.

［6］Vargas M H，Yepez E C，Perez A G，et al.Novel Methodology for Broken-Rotor-Bar and Bearing Faults Detection Through SVD and Information Entropy［J］.Journal of Scientific＆Industrial Research，2012(71):589-593.

［7］周金刚，彭东林，郑方燕，等.基于STM32F4的时栅数控分度转台控制系统［J］.电子器件，2015(5):1138-1143.

［8］ANALOGDEVICES.ADXL335 datasheet［EB/OL］.http://wenku.baidu.com/view/530ea896dd88d0d233d46aed.html?from=search.2011.6.

［9］武紫玉.无刷直流电机滤波器设计方法研究［J］.电气传动，2015(45):37-40.

［10］赵晓风，周璟瑜，王邦均，等.STM32控制下基于GPS与GPRS的轨迹跟踪器［J］.电子器件，2015(38):156-159.

［11］张一舟.基于Savitzky_Golay_省略_合的红外图像非均匀性条带校正方法［J］.中国光学，2015(1):51-60.

［12］周增光.基于质量权重的Savitzky_Golay时间序列滤波方法［J］.遥感技术与应用，2013(2):232-239.

［13］周佳佳.Savitzky_Golay在含冲击负荷短期负荷预测中的应用［J］.电测与仪表，2014，(14):125-128.

褚世凯(1990-)，男，安徽六安人，硕士研究生，现就读与杭州电子科技大学新型电子器件与应用研究所，主要研究风力发电机的振动采集与异常诊断以及嵌入式应用，925820780@qq.com;

秦会斌(1961-)，男，山东泰安人，博士，教授，博士生导师，现为杭州电子科技大学教授，主要研究方向为新型电子器件的研发与应用、抗电磁干扰技术等，qhb@hdu.edu.cn。

Design of W ind Turbine Vibration Acquisition System

CHU Shikai，QIN Huibin*

(Instituteof Electron Devices and Application，Hangzhou Dianzi University，Hangzhou Zhejiang 310018，China)

Aiming at the role of vibration analysis in the condition detection and fault location of wind turbine，the vibration acquisition system is designed based on ADXL335 three axis acceleration sensor，STM32 is used for analog digital conversion.For the frequency aliasing in the process of signal acquisition，a six order Butterworth low-pass filter was designed，and the Savitzky-Golay smoothing algorithm is used for noise signal elimination.Tests indicate the designed filter can effectively filter out the noise signals of above 600 Hz;vibration acceleration error can be controlled within 0.5%;Savitzky-Golay smoothing algorithm can effectively eliminate the noise in the signal.

vibration;wind turbine;ADXL335;butterworth;Savitzky-Golay

C:8260

10.3969/j.issn.1005－9490.2017.01.044

TP277

:A

:1005－9490(2017)01－0232－05

2016-01-08修改日期:2016-02-26