正则的正实部函数的导数估计

郭怡冰 苑文法 庞永峰

(1. 三峡大学 科技学院， 湖北 宜昌 443002； 2. 西安建筑科技大学 理学院， 西安 710055)

正则的正实部函数的导数估计

郭怡冰1苑文法2庞永峰2

(1. 三峡大学 科技学院， 湖北 宜昌 443002； 2. 西安建筑科技大学 理学院， 西安 710055)

本文主要讨论了正则的正实部函数的导数估计问题，即对正则的正实部函数，从已知的三阶，四阶导数估计式，利用归纳法原理及正则的正实部函数的性质推出n阶导数的一般估计式．

正实部函数； 正则函数； 导数； 估计

对于有界正则函数族B={φ(z)|φ(z)=c+c1z+…+cnzn+…，且|φ(z)|<1}中的函数，有熟知的经典不等式

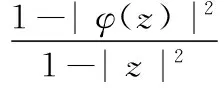
潘一飞、廖孝中[1]对此类函数族进行了研究，得到二阶导数估计式如下：

设φ(z)=c0+c1z+…+cnzn+…在|z|<1内正则，且|φ(z)|<1，则

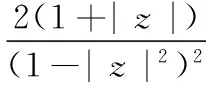
并由此得到，正则的正实部函数的导数估计式：

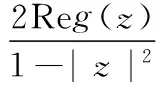
苑文法[2]将正则函数的导数估计推到三阶和四阶，并由此苑文法[3]将正则的正实部函数的导数

估计推到三阶和四阶，得到

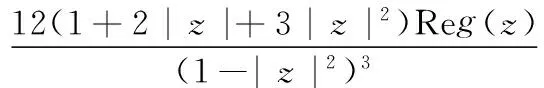
|g(4)(z)|≤

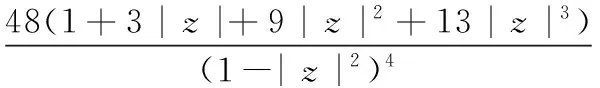
苑文法[4]将有界正则函数的导数估计式推广到一般(n阶)的估计表达式，

本文的目的是对正则的正实部函数的导数估计做进一步的研究，推出正则的正实部函数的导数的估计式．从而将导数估计的问题，从特殊推广到一般．

主要结果：

定理 设g(z)=a0+a1z+…+anzn+…在|z|<1内正则，且Reg(z)>0，则

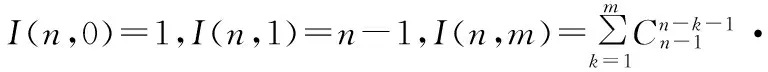
在证明定理之前，引入和证明下面的几个引理．

引理1[5]设φ(z)=c0+c1z+c2z2+…+cnzn+…在|z|<1内正则，|φ(z)|<1，则

成立．其中|s|<1，g0=φ(z)

引理2[5]设φ(z)=c0+c1z+c2z2+…+cnzn+…在|z|<1内正则，|φ(z)|<1，则

成立．

引理3 若g(z)=c0+c1z+c2z2+…+cnzn+…在|z|<1内正则，且Reg(z)>0．则

成立．

证明：考虑函数

由于正实部函数展开式的系数满足：

|an|≤2Re{a0}

故有关系

|G(n)(0)|≤2n！Reg(z)

由引理1，有

则

2n！Reg(z)(n≥1)

利用引理2和三角不等式，并令v=n-j，则有

所以引理3得证．

为证明的简单化，用归纳法来证明定理：

证明：当n=1时，有I(1，0)=1，得

所以，定理成立；

当n=2时，I(2，1)=I(1，0)=1，I(2，0)=1，得

所以，定理成立；

假设当n=k时，估计式成立，即有

下证n=k+1的情形，考虑函数

并对其求n阶导数，令s=0，由引理3可得

将式(5)代入式(6)，得

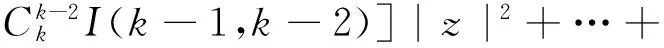
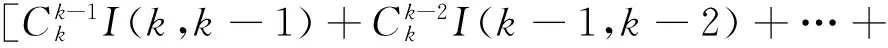
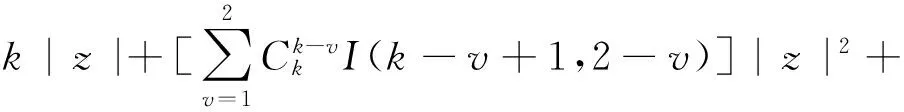
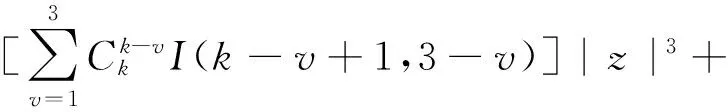
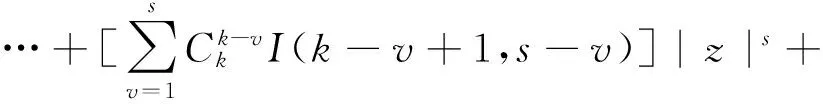
即

故定理得证，即式(1)成立．

从而解决了正则的正实部函数的导数估计问题．

[1] 潘一飞，廖孝中．关于有界函数的导数[J]．江西师范大学学报,1984(1)：21-24．

[2] 苑文法，温金环．关于有界函数的导数的估计[J]．纯粹数学与应用数学，2001,17(4)：358-362．

[3] 苑文法，王玉英，潘智民．正则的正实部函数的导数估计[J]．纯粹数学与应用数学，2004,20(3)：225-227．

[4] 苑文法．有界正则函数的导数估计[J]．数学杂志,2001,21(3)：301-303．

[5] 龚 升．关于Möbius变换的一点注记(一)[J]．纯粹数学与应用数学,1985,1(1)：1-15．

[6] Shaffer D B． On Bounds for the Derivative of Analytic Functions[J]．Proc. Amer. Math. Soc., 1973，37(2)：517-520．

[责任编辑 王迎春]

Estimation of Derivatives forRegular PositiveReal Part Functions

Guo Yibing1Yuan Wenfa2Pang Yongfeng2

(1. College of Science & Technology, China Three Gorges Univ., Yichang 443002, China; 2. College of Science, Xi'an Univ. of Architecture & Technology, Xi'an 710055, China)

The problem of estimating the nth derivative of regular positive real part functions:g(z)=c0+c1z+…+cnzn+…, which are regular in |z|<1 and Reg(z)>0, is discussed. With the principle of inductive method and the characters of regular positive real part functions, an estimation formula of the nth derivative for the functions is presented.

regular positively real part function; regular function； derivatives; estimation

2016-05-04

陕西省自然科学基金(2014JM1010)

郭怡冰(1983-)，女，硕士，讲师，主要研究方向为几何函数论．E-mail：670069604@qq.com

10.13393/j.cnki.issn.1672-948X.2017.04.023

O174

A

1672-948X(2017)04-0110-03