基于光栅衍射的弹性模量小角度测量
2017-09-06邓文浩秦鹏程常相辉刘其军樊代和
孟 赟,邓文浩,秦鹏程,周 昊,常相辉,d,刘其军,d,樊代和,d
(西南交通大学 a.物理科学与技术学院;b.土木工程学院;c.茅以升学院;d.物理国家级实验教学示范中心,四川 成都 611756)

基于光栅衍射的弹性模量小角度测量
孟 赟a,邓文浩a,秦鹏程b,周 昊c,常相辉a,d,刘其军a,d,樊代和a,d
(西南交通大学 a.物理科学与技术学院;b.土木工程学院;c.茅以升学院;d.物理国家级实验教学示范中心,四川 成都 611756)
根据入射光偏转角度与光栅旋转角度的关系,实现了小角度的放大测量,并设计了实验装置应用于弹性模量中金属丝微小伸长量的测量. 理论分析和实验数据表明其角放大倍数可超过传统光杠杆法的放大倍数.
弹性模量;光栅衍射;小角度测量
任何物体在外力的作用下都会发生形变,而弹性模量(杨氏模量)是表征固体材料在弹性限度内抵抗纵向伸长或压缩能力的物理量,是机械设计、建筑工程及材料性能研究中必须考虑的参量. 目前测量弹性模量的方法主要有拉伸法[1]、弯曲法[2]、动态法[3]等,各自有不同的应用场合. 在大学物理实验中常采用静态拉伸法测量金属钢丝的弹性模量. 静态拉伸法实验中给被测钢丝施加一定的拉力F,在其弹性限度内,钢丝会有一定的伸长量ΔL. 弹性模量被定义为应力(钢丝横截面上所受的拉力除以横截面积)与应变(伸长量ΔL与原长L的比值)的比值. 在通常的实验室条件下(1 kg砝码对应的拉力,钢丝原长约0.6 m,直径约0.7 mm),此微小伸长量ΔL在10-4m甚至10-5m数量级[4]. 如此微小的伸长量,在实验中不易直接测量. 目前有报道利用光杠杆法、霍尔位移传感器[5]、迈克耳孙干涉仪法[6]、光电法[7]等方法对此微小量进行放大或者转化来测量.
目前一些教材中采用传统方法——光杠杆法测量微小量ΔL,原理如图1所示[8]. 如考虑反射镜与标尺间的距离为D,光杠杆前后足距离为b,当钢丝有一定伸长量导致光杠杆旋转一定小角度Δθ时,考虑一些近似,2D/b即为光杠杆微小伸长量的放大倍数. 实验中为了能将微小伸长量放大到容易直接测量的数量级范围,即要提高光杠杆的放大倍数,一般通过增加标尺到光杠杆镜面的距离D来实现. 但是,由于增加了D的距离,导致学生在实验过程中一方面要到钢丝旁加载/减载砝码、另一方面又要到望远镜旁读取放大后的读数,这样就导致了实验操作的不方便.
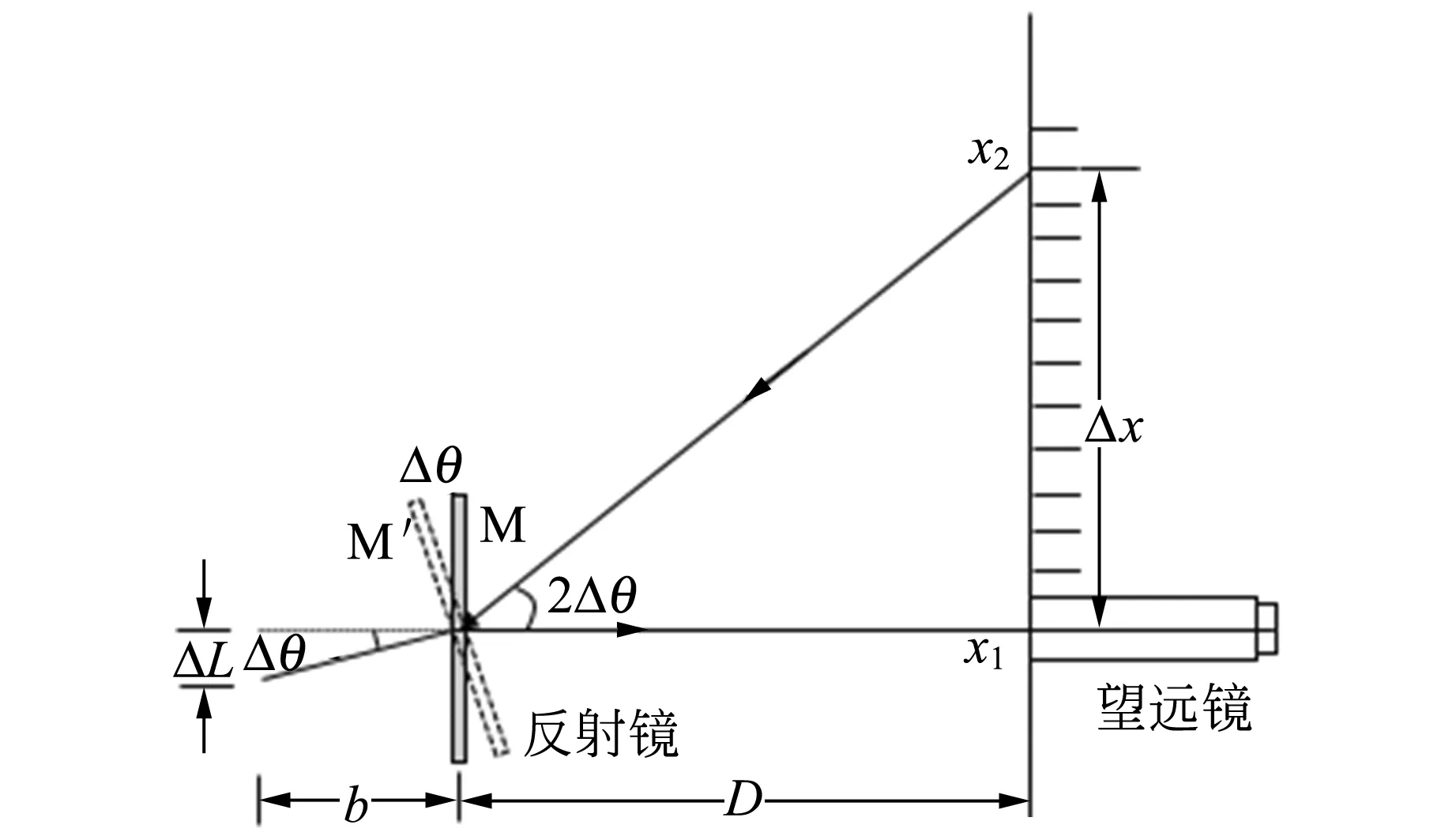
图1 常用光杠杆放大微小伸长量原理图
事实上,一维光栅在微小量测量领域中也有着广泛应用,例如有报道利用光栅的叠栅条纹效应实现了金属丝杨氏模量的测量[9]、利用激光双光栅法实现了微小位移的测量[10]等. 本文提出基于光栅衍射的小角度放大方法,通过理论计算和实际实验结果可知,该方法可以有效地将微小伸长量放大到容易测量的范围,同时可简化实验的操作难度.
1 方案设计
利用光栅代替光杠杆测量微小伸长量的装置如图2所示,其中左侧实线表示入射光线,右侧实线表示入射光未偏转时的零级衍射光,右侧虚线表示第k级衍射光;G为未旋转时的光栅,n为光栅G的法线,θ为未偏转入射光与法线n的夹角;G′为旋转后的光栅,n′为光栅G′的法线,θ′为偏转后的入射光与法线n′的夹角;Δθ为入射光偏转的角度,α为光栅转动的角度. 假设1束平行光(用黑色实线表示)以一定角度入射到一维光栅G的表面,若使第k级衍射光能够沿垂直于光栅G表面的方向(水平方向)出射(图2中黑色虚线所示),则根据光栅方程[11],入射光与光栅G的法线n的夹角需满足:
dsinθ=kλ,k=0,±1,±2,…,
(1)
其中,d=1/N为光栅常量(N为光栅的线数),k为衍射光级次,λ为入射光波长.

图2 方案设计图
当被测钢丝受力有一定的伸长量时,导致入射光线将旋转一定的角度Δθ(如图2中红色实线所示). 此时,为了能够保证光栅的第k级衍射光依然能够沿水平方向出射(图2中黑色虚线所示),则需要将光栅G转动α到G′位置. 此光栅转过一定角度后的光栅方程将变为
d(sinθ′-sinα)=kλ,k=0,±1,±2,…
(2)
通过图2可以得知,
α=θ′-θ-Δθ.
(3)
当选汞灯的绿色谱线(546.1 nm)为入射光、衍射级次为+1级时,根据(1)~(3)式可以得到α及角放大倍数随Δθ的变化关系如图3所示.
从图3可以看出,不论选取N=100 mm-1,N=300 mm-1还是N=500 mm-1线的光栅,α的值明显比Δθ要大很多,也即利用本文提出的方案可以实现小角度的放大功能. 从图3(a)中还可以看出,光栅常量越大,放大效果越好. 图3中的红色“+”表示了利用分光计在实验中实际测得的数据,测量过程如下:a.将分光计调至待测状态,把光栅放到载物台上,此时准直管轴线、望远镜中心轴线能够垂直于光栅平面;b.转动望远镜使得1级衍射光与望远镜光轴重合,此时,可测量得到θ的值;c.调节望远镜转过一个小角度Δθ,此时1级衍射光将偏离望远镜光轴,通过旋转光栅,使1级衍射光能够再次与望远镜光轴重合,此时可以测量得出光栅的偏转角度α,即图3中的实验数据点.

(a)不同光栅常量的α-Δθ的曲线

(b)N=100 mm-1时角放大倍数随Δθ的变化曲线图3 α及角放大倍数随Δθ的变化
可以看出,实验结果与理论曲线吻合得比较好,进一步证明了方案的有效性. 为了更直观地体现本文提出的方案对小角度Δθ的放大效果,图3(b)表示了当选取入射光波长λ=546.1 nm、衍射级次为+1级、N=100 mm-1时,角放大倍数随Δθ的变化关系曲线. 从图中可以看出,Δθ在从0到30′的变化过程中,该方案均可以实现大于50倍的角放大功能,并且,Δθ越小,角放大倍数越大. 例如,当Δθ变化4′时,此时的角放大倍数可达到约150倍. 因此本文提出的方案更适合于小角度的放大应用中.
下面分析选择光栅不同衍射级次以及使用不同入射光波长时,本文提出的方案对小角度的放大情况,如图4所示. 从图4(a)可以看出,当选用N=100 mm-1光栅、入射光波长为λ=546.1 nm时,k=1级衍射的放大效果将优于高级次衍射的放大效果. 从图4(b)可以看出,当选用N=100 mm-1光栅、衍射级次k=1时,入射光波长变化在约100 nm的范围内,对小角度的放大效果区别不是很明显. 但不论哪种情况,均可以将小角度进行角放大. 因此,可以利用本文提出的方案来实现弹性模量测量中小角度的放大功能.
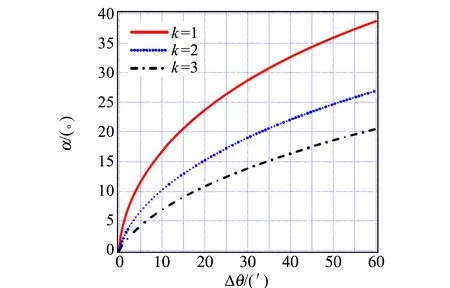
(a)λ=546.1 nm

(b)k=1图4 不同衍射级次、不同入射光波长对Δθ的放大情况
2 弹性模量实验装置设计
如图5所示,将光源连同一狭缝安装在一旋转臂上,旋转臂一端与常用的采用拉伸法测量弹性模量实验中固定被测钢丝的平台相连接,另一端连接在光栅旋转轴上. 同时,将光栅固定于一旋转角度可读的装置上. 初始状态下(钢丝没有被拉伸),调节实验仪器使光栅竖直放置,并使第k级衍射光能水平出射到望远镜(望远镜中设置有水平方向刻线的分划板)的光轴,根据式(1)计算得出入射光与水平方向的夹角θ. 当钢丝受力被拉伸时,将导致入射光相对于初始状态有一小角度Δθ的旋转,此时,通过顺时针旋转光栅,使第k级衍射光仍然能够回到初始时望远镜光轴的位置,并记录光栅旋转过的角度α. 通过α值的大小,即可判断钢丝被拉伸时导致光源旋转过的小角度Δθ=arcsin (sinθ+sinα)-α-θ,结合图5中钢丝到光栅的距离b,则可得出钢丝受力导致的小伸长量为

(4)

图5 杨氏模量测量装置
(4)式表明,实验中一旦确定了常量d,k,λ,b的值,只要能够直接测得较大的角度α,则可以计算得出钢丝受力产生的微小伸长量的值.
考虑到实际的实验过程,被测的钢丝原长为20 cm、直径为0.7 mm、弹性模量E=2×1011N/m2,当受到相当于1 kg砝码的拉力时,其微小伸长量仅为0.026 mm. 如果使用传统的光杠杆法测量(选取D=1 m,b=5 cm,对应放大率为40倍),则只能将此微小伸长量放大到1 mm左右,放大后的值依然较小,较难直接读出. 而如果采用本文提出的装置(选取b=5 cm,N=100 mm-1,λ=546.1,k=1),相同情况下对应的微小旋转角度为1.77′,通过图3(b)可知,本文的装置此时对应的放大率为216倍,也即可将此小角度放大到α=6°24′,事实上,此量级的角度可以容易地直接读出. 由于装置或部件的分量不确定度尚未能获得可靠的技术参量,Δθ的不确定度尚未能作分析评定.
3 结束语
设计了基于光栅偏转控制光衍射方向的测量小角度的实验方案,该方案还可应用于测量弹性模量实验的微小伸长量测量中. 通过研究发现,当选取N=100 mm-1的光栅,同时选取衍射级次为k=1、光源波长为λ=546.1 nm时,可将钢丝受力导致产生的微小伸长量放大到传统仪器可直接方便测量的范围. 与传统使用光杠杆放大的方法相比,本文提出的方案可缩短望远镜到钢丝的距离,降低实验的操作难度. 同时,也对理论方案的一种情形进行了实际实验测量,实验结果与理论预期符合较好. 另一方面,本文提出的方案可获得较大的角放大倍数,而且角度越小,角放大倍数越大,因此特别适合于相关小角度的测量应用.
[1] 庄建,青莉. 关于实验“拉伸法测杨氏模量”的思考[J]. 实验科学与技术,2006,4(3):69-71.
[2] 宋连鹏,孙瑜,刘玉鹏,等. 弯曲法测量圆柱形试样杨氏模量的研究[J]. 物理实验,2016,36(6):22-26.
[3] 吴明阳,朱祥. 动态法测金属杨氏模量的理论研究[J]. 大学物理,2009,28(3):29-32.
[4] 郭涛,盛琛,杨悦. 光杠杆测量杨氏模量的研究[J].大学物理,2016,35(3):40-42.
[5] 游海洋,赵在忠,陆申龙. 霍尔位置传感器测量固体材料的杨氏模量[J]. 物理实验,2000,20(8):47-48.
[6] 徐勋义,张祖豪,刘子健,等. 基于迈克耳孙干涉的金属丝杨氏模量测量[J]. 物理实验,2016(9):19-22.
[7] 陈武军,宗妍,郑新亮. 光电法测量金属丝的杨氏模量[J]. 物理实验,2014,34(12):24-26.
[8] 吴晓立,杨仕君,朱宏娜. 大学物理实验教程[M]. 成都:西南交通大学出版社,2007:41-47.
[9] 孙丽丽,房鑫盛,张家祯,等. 莫尔条纹测量杨氏模量实验研究[J]. 实验科学与管理,2016,33(10):68-75.
[10] 陈思,曾培,周惠君,等. 激光双光栅法测物体微小位移方法的改进与应用[J]. 大学物理,2016,35(1):53-56.
[11] 陆慧. 光学[M]. 上海:华东理工大学出版社,2014:116-131.
[责任编辑:郭 伟]
Small-angle measurement for elastic modulus testbased on grating diffraction
MENG Yuna, DENG Wen-haoa, QIN Peng-chengb, ZHOU Haoc,CHANG Xiang-huia,d, LIU Qi-juna,d, FAN Dai-hea,d
(a.School of Physical Science and Technology; b.School of Civil Engineering;c. Mao Yisheng Honors College; d.National Demonstration Center for ExperimentalPhysics Education, Southwest Jiaotong University, Chengdu 611756, China)
According to the relation between the diffraction angle of the incident light and the rotation angle of the grating, the small-angle measurement was realized. An experimental scheme for measuring the small elongation of metal wire in elastic modulus measurement was provided. Both the theoretical and experimental results showed that the angular magnification exceeded the traditional optical-lever’s magnification.
elastic modulus; grating diffraction; small-angle magnification
2017-03-17
西南交通大学个性化实验项目(No.GX201611126)
孟 赟(1996-),男,山东济宁人,西南交通大学物理科学与技术学院2014级本科生.
樊代和(1981-),男,山西河曲人,西南交通大学物理科学与技术学院讲师,博士,研究方向为光学.
O436.1;O343
A
1005-4642(2017)06-0054-04
