应用于教学实验的水浸超声合成孔径聚焦成像算法
2017-09-06李丹丹王亚平滕永平
李丹丹,吴 迪,王亚平,滕永平
(北京交通大学 理学院 物理系,北京100044)

应用于教学实验的水浸超声合成孔径聚焦成像算法
李丹丹,吴 迪,王亚平,滕永平
(北京交通大学 理学院 物理系,北京100044)
应用JDUT-1B型超声波扫描成像实验仪得到超声B扫描图像,使用延时取整的SAFT成像算法、引入小数延时系数的SAFT成像算法以及SAFT相关性成像算法处理图像. 实验结果表明:处理后的图像较处理前图像的成像效果较为明显,横向分辨率有很大提高,将SAFT成像技术应用于教学实验具有可行性.
水浸超声成像;合成孔径聚焦;横向分辨率
合成孔径聚焦技术(Synthetic aperture focusing technique,SAFT)是20世纪70年代发展起来的成像方法,其最初思想可以追溯到20世纪50年代的合成孔径雷达技术(Synthetic aperture radar,SAR)[1],可以通过较低的工作频率以及较小孔径的换能器获得较高的分辨率[2]. 使用JDUT-1B型超声波扫描成像实验仪容易得到超声B扫描图像,扫描速度快,实验操作简单并且直观,适合普通实验室的物理实验教学. 对SAFT成像算法的研究以及其对图像的处理效果可以使学生对SAFT成像技术有更清晰的认识.
1 合成孔径聚焦成像原理
对于直径为D的换能器,其半功率波束角为

(1)
要提高成像系统的方位分辨率,通常采用2种途径:采用大孔径换能器或应用较高的工作频率[3-4]. 合成孔径聚焦技术是用单个探头移动到不同的位置上进行发射/接收,并通过延时叠加处理信号[5-6],这样就合成为大孔径换能器. 设单个探头的直径为D,在距离探头的垂直距离为R处有一目标点P,超声波的工作波长为λ,合成孔径长度的计算公式为

(2)
其中,c为超声波在介质中的传播速度,f为探头的探伤频率.
1.1 SAFT成像算法:延时取整
如图1所示,探头沿水平方向每隔距离x移动1次,深度方向的采样距离间隔为d,探头的探伤深度为d1. 由(2)式可以计算出合成孔径的长度L,所以合成孔径的阵元数为
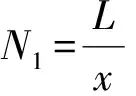
(3)
对求得的N1进行求整、求偶运算[7-8]后即得到探头在合成孔径长度内的移动次数2N.

图1 合成孔径聚焦原理图
探头到目标点的距离可表示为
R=d1+di,
(4)
探头移动到第n个位置时,声程的大小为

(5)
探头在n处接收到信号的延迟时间为
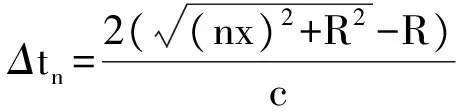
(6)
深度方向采样的时间间隔为
t=d/c .
(7)
1.2 SAFT成像算法:引入小数延时系数
该算法与延时取整的SAFT成像算法基本一致,不同之处是延时取整的SAFT成像算法将小数延时进行四舍五入取整得到整数延时,行信息的变化量为整数. 该算法是利用小数延时算出小数延时系数α[9-10]:
设回波信号表示为S,由整数延时引起的行变化量为i″,所以位置n处的延时回波信号为
S(n)=S(i+i″,j+n)+
α[S(i+i″+1,j+n)-S(i+i″,j+n)].
(8)
将合成孔径内所有位置处对应的点的回波信号叠加并求平均,即可得到点P的重建信号.
1.3 SAFT相关性成像算法
在信号分析中,相关性是指变量之间相互关联的关系. 在超声检测中,噪声之间的相关性很差,缺陷回波信号之间的相关性很好[7]. 该算法是利用超声回波信号之间的相关性处理图像. 设回波信号矩阵为M行、N列. 探头接收到第j列和第j+1列的超声回波信号,则这2列信号之间的相关系数为

(9)
j+1≤N,
其中,

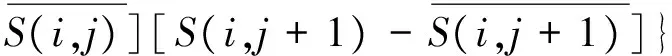
(10)

(11)

(12)
计算出每列回波信号的相关系数rj,选择指数函数e(x)为非线性系数函数. 设合成孔径的波束总数目为2N+1,则重建点为
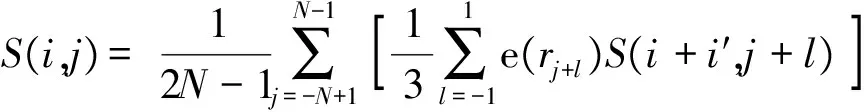
(13)
2 实验方法
实验采用JDUT-1B型超声波扫描成像实验仪,利用水浸法对2根直径约为1 mm的金属丝进行B扫描. 该实验仪结构如图2所示,其采用脉冲式超声波发射接收原理,在计算机的控制下实现超声信号的发射、接收、采集、分析、处理、显示和存储. 该实验仪的优点是操作简单,扫描速度快,学生可以通过电脑直观地观察到超声B扫描图像.

图2 JDUT-1B型超声波扫描成像实验仪
实验采用直径为1 mm的直探头,探伤频率为f=3.3×106Hz,采样数为M×N=459×575. 探头在水平距离采样过程中,每次移动的距离为x=0.25 mm,深度方向的采样间隔为d=0.03 mm,探头的探伤深度为d1=0.059 mm. 改变2根金属丝之间的水平距离,分别采集水平距离为5 mm,3 mm,2 mm时的B扫描数据. 如图3所示,完成数据采集后输入相关参量并且选择算法即可得到处理前后图像. 图3右上图为SAFT处理前图像,右下图为SAFT处理后图像,其中水平轴表示探伤深度方向,竖直轴表示扫描方向.

图3 SAFT成像算法处理界面
3 实验结果
经SAFT算法处理前后的对比图如图4~6所示. 其中,(a)为处理前图像,(b)为延时取整的SAFT成像算法处理后图像,(c)为引入小数延时系数的SAFT成像算法处理后图像,(d)为SAFT相关性算法处理后图像.
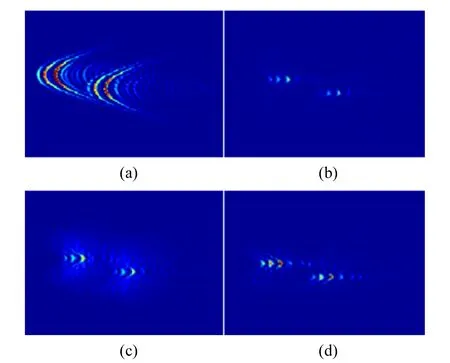
图4 水平距离为5 mm时SAFT处理前后对比图

图5 水平距离为3 mm时SAFT处理前后对比图

图6 水平距离为2 mm时SAFT处理前后对比图
4 实验分析
通过对延时取整的SAFT成像算法、引入小数延时系数的SAFT成像算法以及SAFT相关性成像算法的研究,应用这3种算法处理水浸超声B扫描图像. 通过实验以及数据处理可以得到以下结论:
1)3种算法都能够有效地提高图像的横向分辨率并且图像处理前后效果对比明显.
2)在3种算法中,经引入小数延时系数的SAFT成像算法处理的图像的信噪比较经其他2种算法处理的图像的信噪比低.
3)在3种算法中,经过延时取整的SAFT成像算法以及引入小数延时系数的SAFT成像算法处理的图像的信号幅值较处理前有所下降. 而经SAFT相关性成像算法处理的图像的信号幅值较处理前有所提高,并且信噪比较之前2种算法高.
5 结束语
通过实验及对SAFT成像算法的研究得到了良好的实验效果,将SAFT成像技术应用于教学实验具有可行性. 学生通过实验可以直观地观察到超声B扫描图像的扫描过程,完成数据采集和数据处理,可以即时对图像的处理结果进行分析. 这一过程耗时短,实验简单易操作,可进行多组对比实验,学生通过实验可对SAFT成像技术及其原理有更直观、更清晰的认识.
[1] 王邓志,罗斌,罗宏建. 合成孔径聚焦超声成像系统研究[J]. 东北电力技术,2002(12):42-45.
[2] 蔡兰,兰从庆. 合成孔径聚焦成像方法研究[J]. 武汉工业大学学报,1996,18(1):84-87.
[3] 孙宝申,沈建中. 合成孔径聚焦超声成像(一)[J]. 应用声学,1993,12(3):43-48.
[4] 宋志明,李金龙,王黎等. 合成孔径聚焦成像算法研究[J]. 现代电子技术,2010(23):17-20.
[5] Hoegh K, Khazanovich L. Extended synthetic aperture focusing technique for ultrasonic imaging of concrete [J]. Ndt & E International, 2015,74:33-42.
[6] Li Meng-lin, Guan Wei-jung, Li Pai-chi. Improved synthetic aperture focusing technique with applications in high-frequency ultrasound imaging [J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 2004,51(1):63-70.
[7] 李小娟. 基于合成孔径聚焦技术的轮对探伤成像算法研究[D]. 成都:西南交通大学,2011.
[8] 李小娟,杨昕,王黎,等. 基于合成孔径技术的轮对探伤成像算法研究[J]. 压电与声光,2012,34(4):644-648.
[9] 杜英华. 合成孔径聚焦超声成像技术研究[D]. 天津:天津大学,2010.
[10] 杜英华,张聪颖,陈世利,等. 合成孔径聚焦超声成像方法研究[J]. 海洋技术,2010,29(2):94-96.
[责任编辑:任德香]
Algorithms for water immersion ultrasonic SAFT imagingused in teaching experiment
LI Dan-dan, WU Di, WANG Ya-ping, TENG Yong-ping
(Department of Physics, School of Sciences, Beijing Jiaotong University, Beijing 100044, China)
The ultrasonic B scanning images were obtained using JDUT-1B ultrasonic scanning imaging apparatus, the images were processed by the delay round-off SAFT imaging algorithm, the fractional delay coefficient SAFT imaging algorithm and SAFT correlation imaging algorithm. The results indicated that the original image showed better imaging effect when processed by the algorithms, including the obvious increase of the lateral resolution. Hence the imaging effect of the synthetic aperture focusing imaging technique was more reliable. It was feasible to apply the synthetic aperture focusing imaging technique to teaching experiment.
water immersion ultrasonic imaging; synthetic aperture focusing; lateral resolution
2016-07-09;修改日期:2016-09-14
李丹丹(1990-),女,山东费县人,北京交通大学理学院物理系2015级硕士研究生.
指导教师:滕永平(1965-),男,北京人,北京交通大学理学院物理系副教授,硕士,从事无损检测研究.
O426
A
1005-4642(2017)06-0006-04
