毫米波MIMO系统中迭代最小均方误差混合波束成形算法

2017-09-03申敏徐浩何云周朋光

电信科学 2017年8期

关键词：波束复杂度链路

申敏，徐浩，何云，周朋光

（1. 重庆邮电大学通信与信息工程学院，重庆 400065；2. 重庆邮电大学新一代宽带移动通信重点实验室，重庆 400065）

研究与开发

毫米波MIMO系统中迭代最小均方误差混合波束成形算法

申敏1,2，徐浩1，何云2，周朋光1

（1. 重庆邮电大学通信与信息工程学院，重庆 400065；2. 重庆邮电大学新一代宽带移动通信重点实验室，重庆 400065）

混合波束成形结构能有效解决毫米波MIMO系统中射频链路受限的问题，但要设计性能较优的混合波束成形算法仍然存在困难。为了实现更高的频谱利用率，提出了一种性能较优的迭代最小均方误差（Alt-MMSE）混合波束成形算法。该算法利用数字矩阵的正交特性，首先进行初始数字矩阵设计，然后通过最小化发送信号与接收信号的均方误差不断迭代更新数字矩阵，在每一次迭代过程中，通过更新后的数字矩阵得到模拟矩阵的相位信息。仿真结果表明，与OMP混合波束成形算法和基于矩阵分解的混合处理方案相比，该算法具有更优的性能且更接近于纯数字波束成形。

毫米波MIMO；最小均方误差；混合波束成形；射频链路

1 引言

近些年来随着科技的发展，虚拟现实、自动驾驶等新型技术的出现正逐渐改变人们的生活和工作方式。同时这些新型技术的出现也伴随着移动通信数据业务流量的上升，这对无线通信系统的带宽和传输速率形成了严峻的挑战[1-3]。未来5G通信系统旨在为用户提供 Gbit/s的传输速率，以满足日益增加的用户需求，高的传输速率意味着需要足够量的传输带宽，而现有频谱资源远不能满足 Gbit/s的传输要求，所以研究者们将目光转向毫米波通信技术。

毫米波是指频率在30～300 GHz的电磁波，它具有丰富的频谱资源，受到了众多研究者们的青睐。但由于毫米波具有严重的路径损耗、雨衰现象、穿透损耗等[4]，如何克服毫米波通信过程中的路径损耗已成为一个亟待解决的问题。由于毫米波的波长比较短，这使得它可以在相同的物理尺寸上集成更多的天线，为大规模空间复用和高方向性的波束成形提供了条件，因此研究者们提出利用大规模天线阵列，通过波束成形的方法来克服毫米波传输的信号衰减问题，这使得毫米波波束成形技术成为5G关键技术之一。

传统的波束成形是在数字域实现的，需要为每一根天线配置一条专有的射频链路（RF chain），但由于RF链路的造价较高、功耗大，不宜在系统中大规模使用，所以传统的波束成形仅适用于小规模天线系统。然而，由于毫米波MIMO系统集成了大规模的天线阵列，传统的方法显然不再适用于毫米波MIMO系统。为了解决由于RF受限带来的问题，本文研究毫米波MIMO系统中的混合波束成形问题，通过将大部分的波束成形放在模拟域完成，而在数字基带部分仅使用小维度的数字波束成形，这样以较少数量的RF链路就可以完成信号的波束成形，大大减少了系统的成本和功耗[5,6]。

根据RF链路到天线映射方式的不同，混合波束成形结构分为全连接型和部分连接型[5]，全连接型混合波束成形结构中 RF链路与所有的天线相连，因此能够获得天线的全部波束成形增益。基于毫米波信道的稀疏性，参考文献[7]提出了一种OMP（orthogonal matching pursuit，正交匹配追踪）混合波束成形算法，该算法通过纯数字波束成形矩阵与混合波束成形矩阵的误差矩阵，从候选集合中迭代更新模拟波束成形矩阵，最终得到性能较优的混合波束成形算法，但是该算法在信道不满足稀疏性时得到的速率与理论值之间存在较大的差别。参考文献[8]利用数字波束成形矩阵的正交特性，提出了一种低复杂度的混合波束成形算法，避免了矩阵的伪逆运算，具有较低的算法复杂度。参考文献[9]提出一种基于波束训练的混合波束成形算法，但是由于在实际系统中移相器精度有限，所以该算法并不能达到最优的性能。参考文献[10]研究了数据流数与RF链路数之间的关系对系统性能的影响，并指出当RF链路数等于数据流数的两倍时，混合波束成形可以得到近似于纯数字波束成形的系统性能。参考文献[11]提出了一种基于矩阵分解的混合处理（matrix decomposition based hybrid processing，MD-HP）方案，该方法通过不断收敛模拟矩阵的相位，并以此更新数字矩阵和模拟矩阵，可获得近似于纯数字波束成形的系统性能。

目前针对部分连接混合波束成形的研究相对较少，部分连接结构的特点是RF链路只与部分天线相连，因此基于该结构的混合波束成形算法的成形增益要小于全连接的方式，但是由于将天线进行分组，所以部分连接方式的混合波束成形是以牺牲部分增益换取较低的复杂度。参考文献[12]提出了一种基于码本的混合波束成形设计方案，尽管该算法复杂度较低，但系统性能有所损失。参考文献[13]在串行干扰消除（successive interference cancellation，SIC）思想的基础上，提出了一种部分连接混合波束成形算法，但是该算法的全部增益都来自于模拟矩阵，因此只能实现次优的性能。参考文献[8]提出的 SDR-AltMin算法，相比参考文献[13]的算法虽然性能有所提升，但由于设计条件比较苛刻仍不能实现最优的性能。

基于以上分析，为了获得较优的系统性能，本文针对全连接结构提出了一种迭代最小均方误差（alternating minimum mean square error，Alt-MMSE）算法。该算法以最小化收发信号的均方误差为目的，利用数字矩阵的正交特性，在初始数字矩阵的基础上不断迭代更新数字矩阵和模拟矩阵。与传统OMP算法和参考文献[11]中的MD-HP算法相比，该算法的优点是综合考虑发送端波束成形矩阵和接收端合并矩阵的影响，在保证收发信号误差最小的前提下，交替更新波束成形矩阵和合并矩阵使其趋向最优，从而提高系统性能。

2 系统模型

2.1 系统描述本文研究单用户MIMO系统中混合波束成形算法，系统框架如图1所示。考虑配置Nt条发射天线和NRF条射频链路的基站使用N条数据流，ts与配置Nr条接收天线和NrRF条射频链路的用户进行数据通信。发送端和接收端的数据流数、天线个数和RF链路数三者分别满足Ns≤NtRF≤Nt，N≤NRF≤N。srr

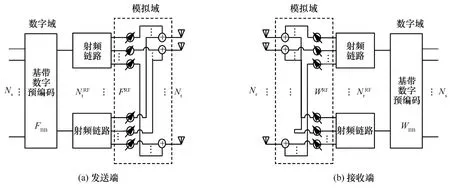
图1 毫米波MIMO系统框架

本文字母做如下定义：大写字母A表示矩阵，小写字母x表示列向量，A−1表示矩阵A的逆，A*表示矩阵的共轭转置，diag(⋅)表示对角矩阵，A[ :,[1:a ]]取矩阵A的前a列，|| A ||2F表示矩阵A的Frobenius范数， A†表示A的伪逆， Tr( A)表示求矩阵的迹。

调制后的符号首先经过数字波束成形矩阵F∈CNtRF×Ns进行基带信号处理，处理后的信号再BB经过模拟波束成形矩阵 F∈CNt×NtRF形成最终的RF发送信号：

其中， s=[s ,L ,s ]T∈CNs。1 Ns

本文采用Saleh-Valenzuela（萨利赫—巴伦苏埃拉）信道模型[6]，H ∈CNr×Nt表示下行信道矩阵，则接收信号y表示为：

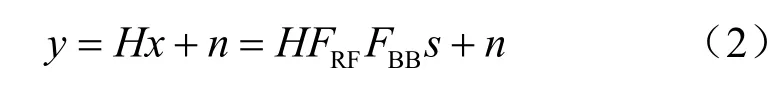
其中，噪声矢量n服从均值为0、方差为 σ2I的高斯分布，即n～C N (0,σ2I)。

用W∈CN×NRF、W ∈CNrRF×Ns分别表示模拟rr RF BB合并矩阵和数字合并矩阵，假设收发端已知信道的状态信息，则接收信号y在经过模拟域和数字域的信号处理后的接收符号矢量可表示为：

模拟合并矩阵 WRF和模拟波束成形矩阵 FRF是通过在收发端使用具有调相功能的移相器实现的，因为调幅能力有限，所以模拟波束成形矩阵和合并矩阵元素一般满足恒模约束在信道状态信息已知的情况下，系统的频谱效率[10]R可表示为：

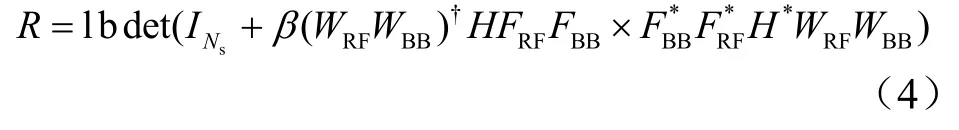
2.2 信道模型

毫米波通信的一个显著特点是传输路径中散射体的数量比较少，所以已有信道模型[14]并不适用于毫米波通信系统。针对这种情况，采用Saleh-Valenzuela模型[6]，该模型下的毫米波信道矩阵H可表示为：

信道矩阵的矩阵表达形式为：

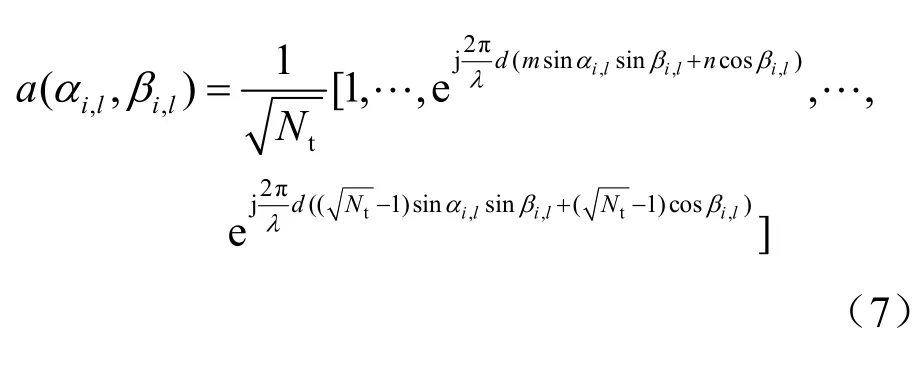
其中，m、n分别为二维平面阵列的索引值，对收发端的天线阵列，m、n的取值分别为d为天线间距，λ为信号波长。

2.3 问题定式化

在传统的数字预编码结构中，考虑到算法的复杂度加上毫米波 MIMO系统本身的复杂性，所以在实际的系统中常常采用线性预编码算法，MMSE算法就是常用的一种方法，通过最小化式（8）中的目标函数，得到最终的预编码矩阵：

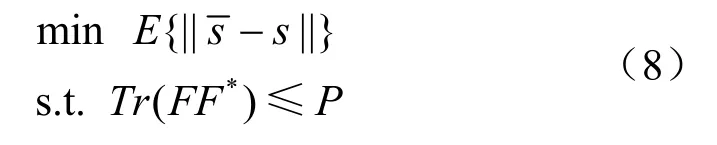
其中，F满足发送端功率限制要求，P表示发送端平均发送功率。

对于采用两级处理的混合波束成形结构，式（8）中的目标函数可以进一步写成：

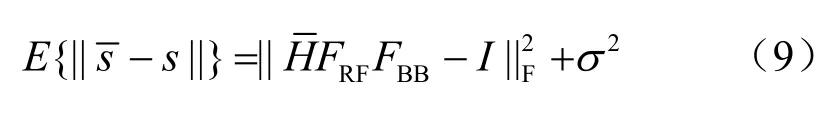
本文所提算法就是对式（9）中的目标函数的进一步等价，并通过迭代得到性能接近纯数字波束成形的混合波束成形算法。

3 Alt-MMSE混合波束成形算法

在传统的MMSE算法的基础上，通过利用数字矩阵的正交特性，结合迭代更新的思想，提出一种迭代MMSE（Alt-MMSE）算法，该算法首先设计初始数字矩阵，并在此基础上迭代更新，最终得到混合波束成形矩阵。

3.1 初始数字波束成形矩阵设计

对信道矩阵H进行奇异值分解（singular value decomposition，SVD）：

其中，U 表示 Nr× Nr阶酉矩阵，S表示Nr× Nt阶奇异值矩阵，V表示 Nt× Nt阶酉矩阵。取矩阵V的前 Ns列作为纯数字波束成形矩阵Fopt: Fopt=V (:,[1:Ns])。

而在混合波束成形结构中，由于存在两级的波束成形矩阵，故不能直接使用传统的MMSE算法，因此采用等效矩阵的方法获得初始数字矩阵：

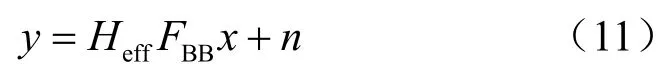
其中， Heff= HFRF，对等效信道矩阵进行奇异值分解 Heff=UeffSeffVe*ff，则有：

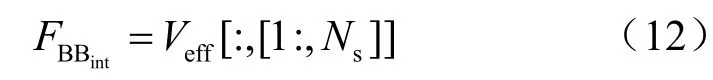
为了使该算法的性能更趋近于纯数字波束成形矩阵，令：

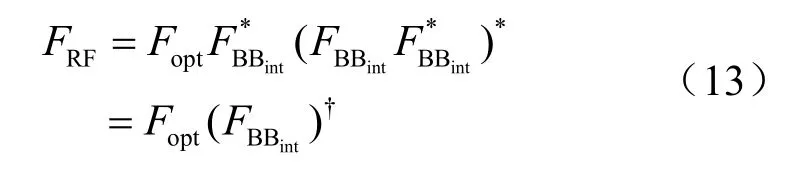
此时有：

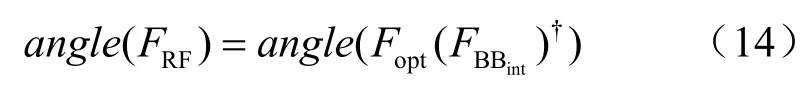
由式（14）可以得到满足恒模要求的模拟波束成形矩阵。

3.2 Alt-MMSE算法设计

本文所提算法的目的是减小收发信号的最小均方误差，在初始数字矩阵的基础上，利用数字矩阵的正交特性，进一步简化式（9）中的目标函数，对简化后的目标函数进行多次迭代，最终得到数字模拟混合波束成形矩阵。

对式（9）中的目标函数进行展开[8]：

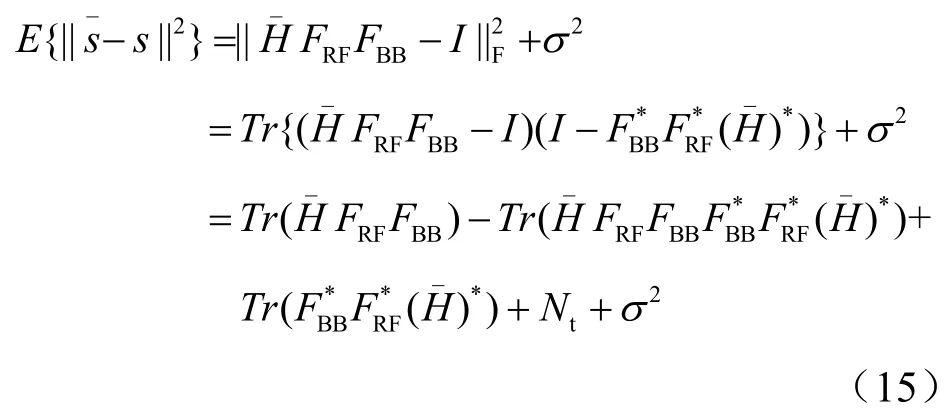
利用数字波束成形矩阵的正交特性，即：F F*= I，在假设 F 已知的情况下，式（15）BBBBRF可以进一步转化为：

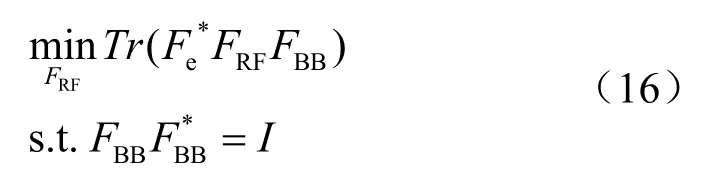
通过式（16）可以近似得到收发信号的最小均方误差，由赫尔德不等式可知：

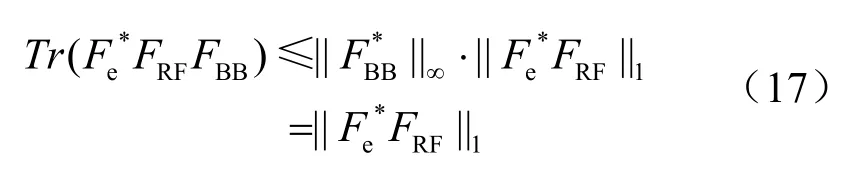
只有当BBF 满足式（18）时等式成立：

其中， Fe*FRF= USV*。由于模拟矩阵各元素满足恒模要求，所以根据式（14）得到的模拟波束成形矩阵各元素值的相位信息，可以进一步得到模拟矩阵 FRF， arg(FRF) =arg(FoptFB†B)。将更新后的数字矩阵 FBB和模拟矩阵 FRF作为下一次更新使用的初始条件，在每一次的迭代过程中，利用式（14）得到满足恒模要求的模拟矩阵，使设计的混合波束成形矩阵逼近纯数字波束成形矩阵，从而提高系统的性能，具体算法如下。

算法1 Alt-MMSE混合波束成形算法

输入： H, FRF,WRF

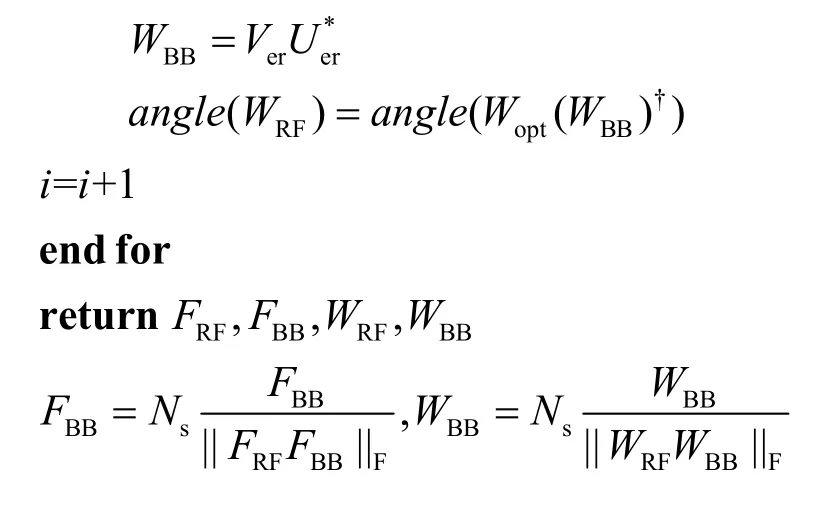
4 仿真和复杂度分析

4.1 仿真分析

本文通过仿真验证在不同数据流数、不同射频链路数以及SNR=0的情况下所提Alt-MMSE算法的性能，并与纯数字波束成形、OMP混合波束成形算法[7]以及参考文献[11]中的MD-HP方案进行了对比。具体仿真参数见表1。

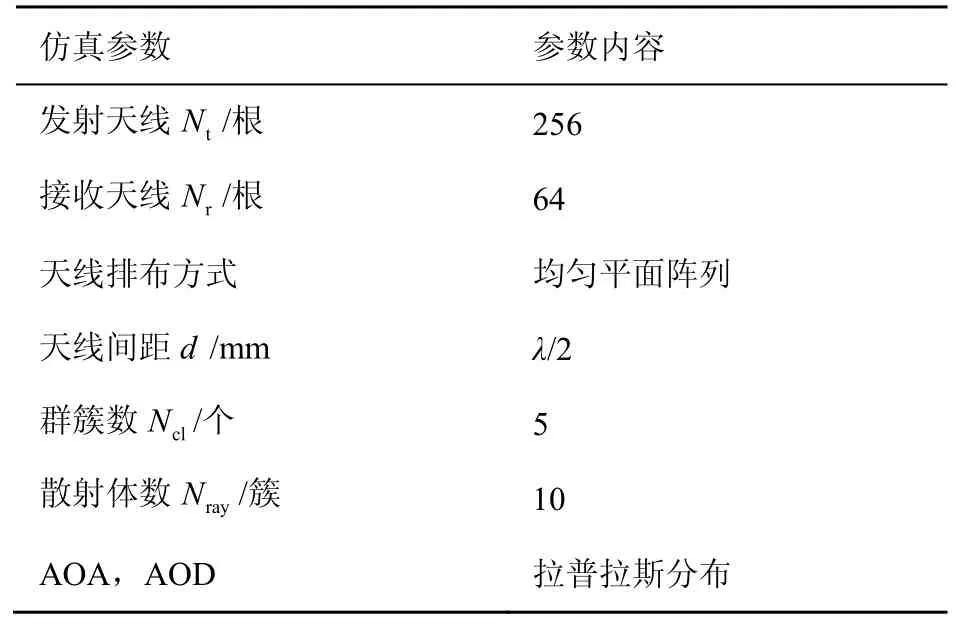
表1 仿真参数

图 2表示在 RF链路数 NtRF= NrRF=8、Ns= {2,4,8}时Alt-MMSE算法、纯数字波束成形算法和 OMP算法得到的系统性能随信噪比变化的曲线。由图2可知，在数据流数较少时，3种算法的性能差距不大，但随着数据流数 Ns的增加，3种算法性能的差距越来越明显，Alt-MMSE算法的性能明显优于OMP算法的性能，且更接近于纯数字波束成形的性能。该仿真表明，当数据流数较大时，Alt-MMSE算法的性能优势明显大于基于 OMP的混合波束成形算法。

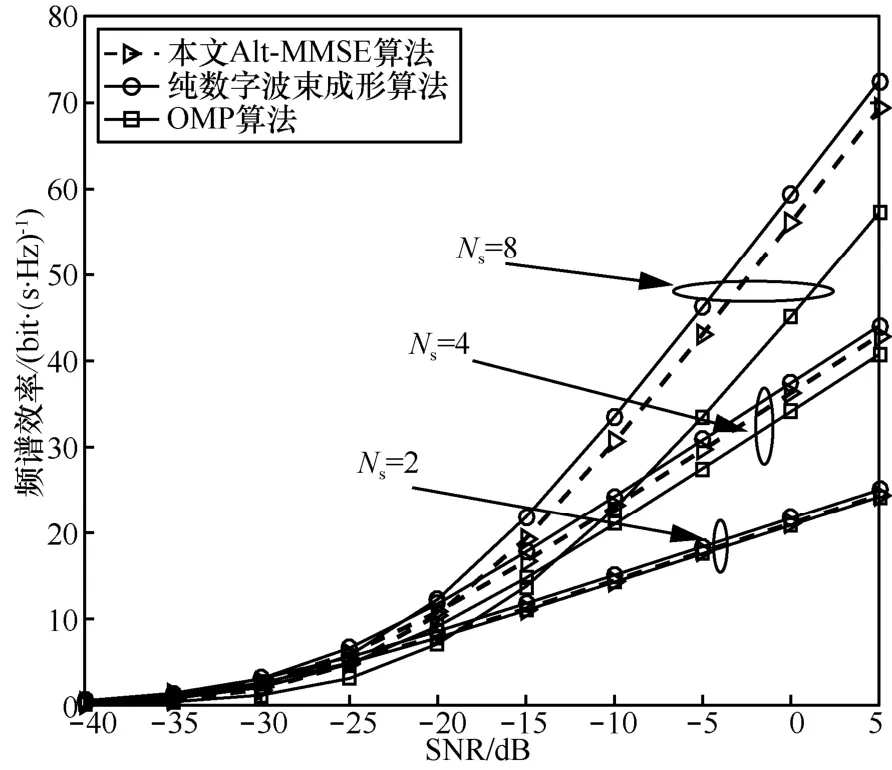
图2 RF链路数 NtRF=NrRF= 8、数据流数 Ns = {2,4,8}时的系统性能

图3表示在NtRF= NrRF= Ns= {2,4,8}时3种算法的系统性能随信噪比变化的曲线。由图3可知，当数据流数等于RF链路数时，基于OMP的混合波束成形算法的性能明显低于纯数字波束成形的性能，且随着数据流数的增加差距越来越明显，Alt-MMSE算法的性能始终优于 OMP算法的性能，且十分接近纯数字波束成形算法的系统性能。由此可以看出，RF链路数与数据流数的关系也会影响算法的性能。

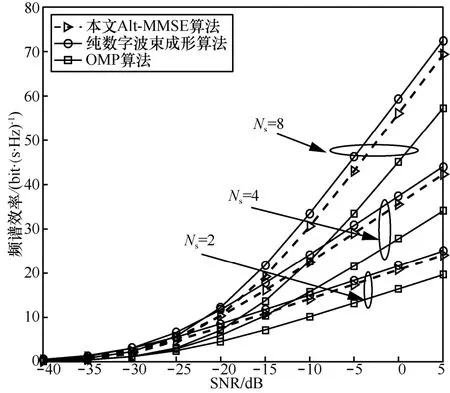
图3 NtR F = NrR F= Ns = {2,4,8}时的系统性能

图4表示当SNR=0、 Ns={2,4,8}时3种算法的性能随RF链路数的变化趋势。由图4可知，当数据流数一定时，RF链路数对系统性能有明显的影响，当RF链路数较少时，本文Alt-MMSE算法的性能相比OMP算法具有明显的优势。当RFs2N N≥时，两种算法的性能变化曲线趋于平稳。RF链路数的增加虽然带来了系统性能的提升，但同样也带来了成本和功耗的增加，所以在实际系统应用中应综合考虑两者对系统性能的影响。此外，图4进一步解释了图2和图3中不同RF链路数对系统性能的影响，即当数据流数相同时，RF链路数越大，算法的性能越好。这也是造成图3中3种算法的性能差异大于图2中算法间性能差异的主要原因。

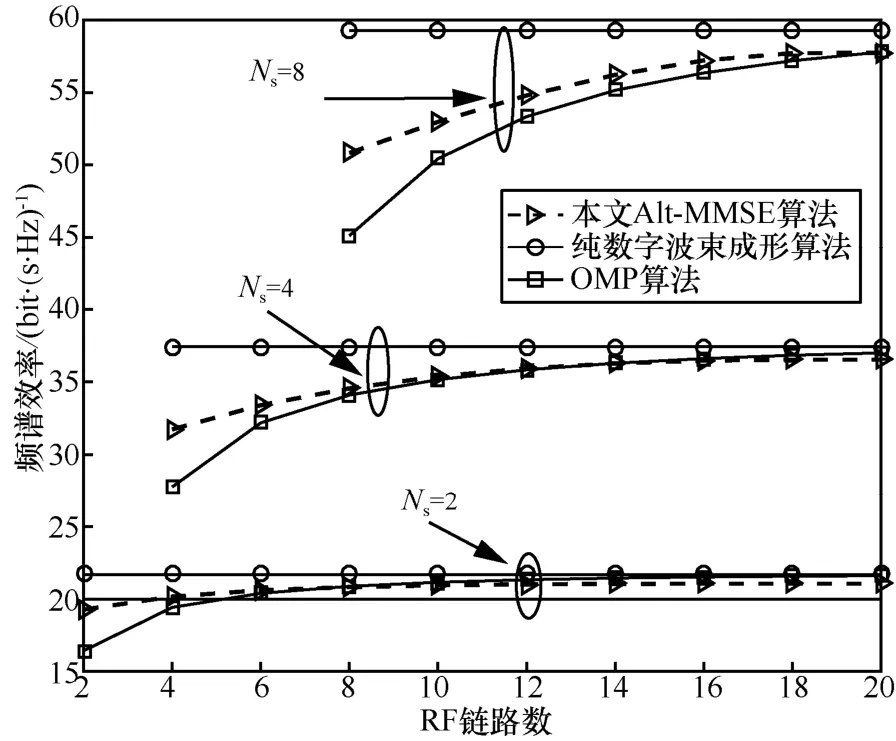
图4 SNR=0、 Ns= {2,4,8}时的系统性能

图5表示当 NRF= NRF= 8、 N ={4,8}时AlttrsMMSE算法、纯数字波束成形算法以及参考文献[11]提出的近似最优MD-HP方案3种算法的性能随SNR的变化趋势。由图5可知，不同于经典的OMP混合波束成形算法，本文所提Alt-MMSE算法的性能略优于MD-HP方案的性能，且均能取得近似于纯数字波束成形的频谱效率。

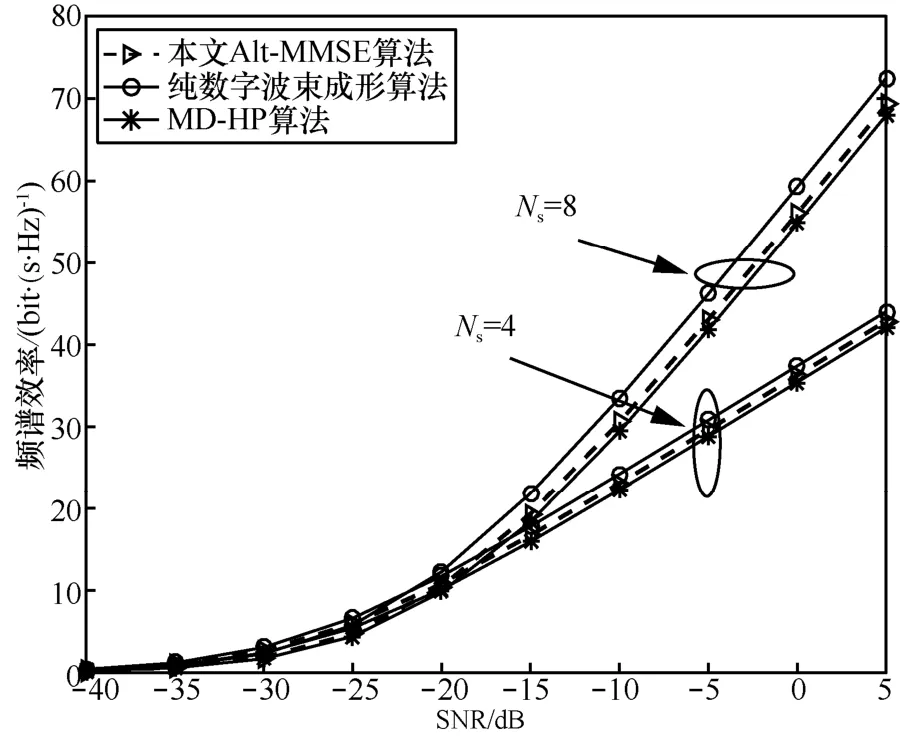
图5 N RF = NRF= 8、 N= {4,8}时的系统性能trs

4.2 复杂度分析

在第4.1节中所给参数的条件下，对比分析3种算法的复杂度[15,16]。参考文献[7]中的OMP混合波束成形算法利用纯数字矩阵和混合波束成形矩阵的误差矩阵，从候选集合中迭代更新混合波束成形矩阵，它的算法复杂度主要由计算候选集合和误差矩阵的相关性决定，并以此选出合适的模拟波束成形矢量，复杂度为 O( Nt2NtRF2Ns)。参考文献[11]中的MD-HP算法，利用模拟矩阵 FRF的相位信息进而更新数字矩阵 FBB的过程，其中涉及模拟矩阵的伪逆运算，它的算法复杂度为 O( NtNtRF2)。本文所提Alt-MMSE算法不同于以上两种算法，通过数字矩阵 FBB矩阵得到模拟矩阵 FRF的相位信息，并以此构造出模拟波束成形矩阵，它的算法复杂度主要来自算法1步骤5中等效矩阵的计算，所以 Alt-MMSE的复杂度为O( NtNtRFNs)。在实际的系统中，由于因此相比OMP算法[7]和MD-HP算法[11]，本文所提Alt-MMSE算法具有较低的复杂度。

5 结束语

本文研究了毫米波MIMO系统中混合波束成形问题，为了得到近似于纯数字波束成形的系统性能，提出了一种迭代更新最小均方误差算法，该算法通过利用数字矩阵的正交特性，在初始数字矩阵的基础上，通过最小化收发信号的最小均方误差，结合纯数字波束成形矩阵，不断迭代更新数字矩阵和模拟矩阵。通过与经典OMP算法以及参考文献[11]中的近似最优MD-HP算法对比，所提系统性能明显优于OMP算法，尤其是当RF链路数等于数据流数且数量较少时，所提算法的性能始终近似于纯数字波束成形的性能。与近似最优MD-HP方案相比，所提性能略优于MD-HP算法，且均接近纯数字波束成形的性能。在算法的复杂度方面，相比OMP算法和MD-HP算法，本文所提Alt-MMSE混合波束成形具有较低的算法复杂度。

[1]ANDREWS J G, BUZZI S, WAN C, et al. What will 5G be?[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(6): 1065-1082.

[2]YONG S K, CHONG C C. An overview of multigigabit wireless through millimeter wave technology[J]. EURASIP Journal on Wireless Communications and Networking, 2007(1): 1-10.

[3]RAPPAPORT T S, SUN S, MAYZUS R, et al. Millimeter wave mobile communications for 5G cellular: it will work![J]. Access IEEE, 2013, 1(1): 335-349.

[4]CHOUDHURY D. 5G wireless and millimeter wave technology evolution: an overview[C]//2015 IEEE MTT-S International Microwave Symposium, May 17-22, 2015, Phoenix, SA, USA. New Jersey: IEEE Press, 2015: 1-4.

[5]HAN S, CHIH-LIN I, XU Z, et al. Large-scale antenna systems with hybrid analog and digital beamforming for millimeter wave 5G[J]. IEEE Communications Magazine, 2015, 53(1): 186-194.

[6]KWON G, SHIM Y, PARK H, et al. Design of millimeter wave hybrid beamforming systems[C]//2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall), September 14-17, 2014, Vancouver, Canada. New Jersey: IEEE Press, 2014: 1-5.

[7]EL A O, RAJAGOPAL S, ABU-SURRA S, et al. Spatially sparse precoding in millimeter wave MIMO systems[J]. IEEE Transactions on Wireless Communications, 2013, 13(3): 1499-1513.

[8]YU X, SHEN J C, ZHANG J, et al. Alternating minimization algorithms for hybrid precoding in millimeter wave MIMO systems[J]. IEEE Journal of Selected Topics in Signal Processing, 2016, 10(3): 1.

[9]TSANG Y M, POON A S Y, ADDEPALLI S. Coding the beams: improving beamforming training in mmWave communication system[C]//IEEE Global Telecommunications Conference, December 5-9, 2011, Houston, TX, USA. New Jersey: IEEE Press, 2011: 1-6.

[10]SOHRABI F, YU W. Hybrid digital and analog beamforming design for large-scale antenna arrays[J]. IEEE Journal of Selected Topics in Signal Processing, 2016, 10(3): 501-513.

[11]NI W. Practical system implementation for 5G wireless communication systems[D]. Victoria: University of Victoria, 2015.

[12]SINGH J, RAMAKRISHNA S. On the feasibility of codebook-based beamforming in millimeter wave systems with multiple antenna arrays[J]. IEEE Transactions on Wireless Communications, 2014, 14(5): 2670-2683.

[13]DAI L, GAO X, QUAN J, et al. Near-optimal hybrid analog and digital precoding for downlink mmWave massive MIMO systems[C]//2015 IEEE International Conference on Communications (ICC), June 8-12, 2015, London, UK. New Jersey: IEEE Press, 2015: 1334-1339.

[14]赵雄文, 高波. MIMO信道仿真模型比较及其验证[J]. 电信科学, 2016, 32(2): 75-82. ZHAO X W, GAO B. Comparisons and validations on MIMO channel simulation models[J]. Telecommunications Science, 2016, 32(2): 75-82.

[15]CORMEN T H, LEISERSON C E, RIVEST R L, et al. Introduction to algorithms, second edition[M]. Beijing: DBLP, 2001.

[16]向建伟, 于秀兰, 景小荣. 毫米波大规模MIMO系统中低复杂度混合预编码方法[J]. 电信科学, 2016, 32(9): 10-15. XIANG J W, YU X L, JING X R. Low complexity hybrid precoding method in mmWave massive MIMO system[J]. Telecommunications Science, 2016, 32(9): 10-15.

Alternating minimum mean square error hybrid beamforming algorithm in mmWave MIMO system

SHEN Min1,2, XU Hao1, HE Yun2, ZHOU Pengguang1
1. School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China 2. Key Lab of New Generation Broadband Mobile Communication, Chongqing University of Posts and Telecommunications, Chongqing 400065, China

The two-stage hybrid beamforming architecture can solve the problem of limited number of RF chains effectively. However, it is still difficult to design a hybrid beamforming algorithm with better performance. In order to achieve higher spectral efficiency, an alternating minimum mean square error (Alt-MMSE) hybrid beamforming algorithm was proposed. Firstly, the initial digital matrix by using the orthogonal properties of the digital matrix was designed, and then the digital matrix by minimizing the square error of the transmitted signal and the

signal was updated. During each iteration, the phase of the analog matrix could be obtained from the updated digital matrix and the optimal fully digital matrix. The simulation results show that the proposed algorithm has better performance and is closer to fully digital beamforming than OMP hybrid beamforming algorithm and hybrid processing scheme based on matrix decomposition .

mmWave MIMO, minimum mean square error, hybrid beamforming, RF chain

The National Science and Technology Major Project of China (No.2016ZX03002010-003)

TN929.5

10.11959/j.issn.1000?0801.2017205