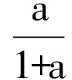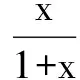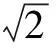函数单调性的应用
2017-09-03杜红全
杜红全
(甘肃省康县教育局教研室,甘肃 陇南 746500)
函数单调性的应用
杜红全
(甘肃省康县教育局教研室,甘肃 陇南 746500)
单调性是函数之“魂”,是函数的重要性质之一,文章举例说明它在比较大小、解不等式、解方程、求参数的值或取值范围、求函数的最值或值域、求值、证明不等式等方面得一些应用,希望起到抛砖引玉之功效.
函数;单调性;应用
函数单调性是函数的重要性质之一,也是平常考试和高考中数学的重点和热点内容之一.它在高中数学的各个分支中都有着极为重要的应用,在解题过程中如果应用得好,常能起到事半功倍的效果,下面举例说明.
一、比较大小
例1设函数f(x)是(-∞,+∞)上的减函数,则( ).
A.f(a) C.f(a2+a) 分析 由减函数的定义可知,只需比较各组函数值的自变量的大小. 点评 本题还可以用排除法解之.利用单调性比较大小时,必须将其转化为同一单调区间内的两个函数值,否则不能比较其大小. 例2 已知f(x)在它的定义域[-17,+∞)上是增函数,且f(3)=0,解不等式f(x2-7x-5)<0. 分析 解本题只需要利用函数的单调性去掉函数关系符号“f”, 使抽象的不等式问题转化为具体的不等式问题. 点评 利用单调性解不等式就是利用函数在某个区间内的单调性,推出两个变量的大小,然后去解不等式;去掉函数关系符号″f″的主要依据是函数的单调性,同时要特别注意函数的定义域,否则可能产生增解. 例3 解方程(x2-x+1)5-x5+4x2-8x+4=0. 解析 由原方程变形为(x2-x+1)5+4(x2-x+1)=x5+4x.由于函数f(t)=t5+4t在R上单调递增,又f(x2-x+1)=f(x),所以x2-x+1=x,解得x=1.故原方程有唯一实数解x=1. 点评 解本题的关键是对原方程进行变形,与函数f(t)=t5+4t产生联系,再根据函数的单调性列出方程即可. 例4 若函数f(x)=|2x+a|的单调递增区间是[3,+∞),则a=____. 点评 本题考查的是函数的单调性.做本题的关键是将原函数化为分段函数,然后根据单调递增区间列出关于a的方程即可.本题还可通过画出函数图象来求解. 例5 已知函数f(x)=x2+2(1-a)x+2在(-∞,4]上是减函数,求实数a的取值范围. 分析 二次函数是我们最熟悉的函数,只要遇到二次函数画图象,也可以不将图象画出,而在大脑中出现,这样就给我们研究问题带来了很大的方便.对于不熟悉的函数,可以利用单调函数的定义去研究与单调性有关的问题. 点评 二次函数问题要注意三点:一是开口方向;二是对称轴;三是顶点坐标. 分析 当所给的函数图象不易作出时,可考虑利用函数的单调性求函数的最值,即先判断函数的单调性,再求最值. 点评 函数f(x)在区间[a,b](a 例7 设实数a,b满足条件a3-3a2+5a=1,b3-3b2+5b=5,求a+b的值. 分析 待求代数式的值,可视为相应函数的一个特殊值,再利用该函数的单调性,把函数值的相等转化为自变量的相等,从而巧妙获解. 解 由已知条件式的特征,构造函数f(x)=x3-3x2+5x,则有f(a)=1,f(b)=5.而f(x)=(x-1)3+2(x-1)+3.令u=x-1,则g(u)=u3+2u是单调增函数,还是奇函数,则有f(a)=g(a-1)+3=1,f(b)=g(b-1)+3=5,即g(a-1)=-2,g(b-1)=2,则g(a-1)=-g(b-1)=g(1-b).由g(u)=u3+2u是单调增函数可得a-1=1-b,因此有a+b=2. 点评 求解本题的关键是构造函数f(x)=x3-3x2+5x,利用函数的单调性和奇函数的性质,列出关于a,b的方程,把a+b整体解出,属于整体求值. 分析 通过构造函数转化为比较单调函数的两个函数值问题. 点评 把证明的不等式问题转化为函数问题,关键在于转化为什么样的函数,这就要求从被证的不等式的形状、特点去入手,产生联想去寻找相应的基本函数,然后利用函数的单调性加以证明. 当然,利用函数的单调性还可以判断复合函数的单调性以及画函数的图象,在这里就不举例说明了. 链接高考 1(2015江苏,文理7)不等式2x2-x<4的解集为 .(答案:{x|-1 2(2016全国Ι卷,理8)若a>b>1,0 A.ac C.alogbc [1]杜红全.别忘了让平面向量与三角形谈“心”[J].中学生数学,2014(3). [2]杜红全.求三角函数值域的常用方法[J].中学生数学,2014(5). [责任编辑:杨惠民] 2017-05-01 杜红全(1969.9-), 男,甘肃康县人,中学高级教师,西北师范大学本科毕业,从事中学数学教育. G632 B 1008-0333(2017)19-0002-02
二、解不等式
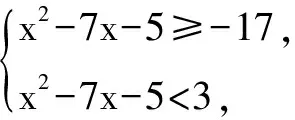
三、解方程
四、求参数的值或取值范围
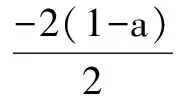
五、求函数的最值或值域
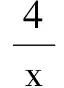

六、求值
七、证明不等式