趋势项分离预测模型及重标度极差分析在深基坑变形预测中的应用研究

王雪妮， 韩国锋

(1. 杨凌职业技术学院， 陕西 咸阳 712100； 2. 陕西铁路工程职业技术学院， 陕西 渭南 714000)

趋势项分离预测模型及重标度极差分析在深基坑变形预测中的应用研究

王雪妮1， 韩国锋2

(1. 杨凌职业技术学院， 陕西 咸阳 712100； 2. 陕西铁路工程职业技术学院， 陕西 渭南 714000)

为解决基坑变形预测精度低的问题，利用小波去噪和卡尔曼滤波对基坑变形序列进行去噪处理，分离趋势项及误差项，并利用支持向量机和BP神经网络分别对趋势项和误差项进行预测，以掌握基坑的变形规律及发展趋势； 同时，采用重标度极差分析(R/S分析)对基坑的变形趋势进行判断，以验证变形预测的可靠性。根据实例检验，得出小波去噪的去噪效果较好，且预测结果的相对误差均值为1.03%，方差值为0.083，预测精度较高；基坑的变形序列与速率序列均具有持续增长的趋势特征，与变形预测结果一致，验证了预测思路的有效性。

深基坑； 变形预测； 去噪分析； 支持向量机； R/S分析； 趋势判断

0 引言

随着近年来城市建设的快速发展，深基坑的应用越来越广泛，但由于基坑施工对地质环境的改变，使得基坑开挖以后会出现不同程度的变形，而变形会对基坑自身、周边建筑及关系带来影响，甚至诱发安全问题，如广州海珠区在2005年发生了一起深基坑坍塌的安全事故，杭州市在2008年也发生了一起深基坑的坍塌事故； 因此，对基坑的变形进行监测及研究，且根据监测数据进行分析及预测，已成为判断基坑稳定性及避免周边建筑被破坏的重要手段[1-3]。

近些年，相关学者将支持向量机和神经网络引入到基坑的变形预测中。例如： 渠孟飞等[4]、林楠等[5]利用支持向量机对深基坑的变形进行了预测研究，经实例检验，得出该模型在深基坑中的预测精度较高，能有效判断基坑的发展趋势，达到对基坑安全监控的目的；张世豪等[2]、曾晖等[6]利用BP神经网络对基坑的变形进行预测，得到预测结果与实测值吻合度较好，且具有精度与效率兼顾的特点。然而基坑变形数据难免会受到环境因素的影响，使得监测值与真实变形值存在一定差异，小波去噪和卡尔曼滤波方法能从监测数据中提取出真实的变形数据[1,7]，具有较好的适用性。

上述研究虽然取得了一定的成果，但多是将趋势分析及变形预测独立进行研究，缺少两者的综合应用； 因此，采用小波去噪和卡尔曼滤波对基坑变形数据进行去噪处理，将最优去噪结果作为趋势项和误差项的分离依据，并利用支持向量机和BP神经网络分别对两序列进行预测，由两者的预测结果综合得到预测值。同时，为验证预测结果的准确性，再将R/S分析方法引入到基坑的变形趋势判断中[8]，以期达到对基坑变形的综合变形趋势判断。

1 基本原理

1.1 支持向量机

支持向量机是一种基于统计学开发的数据挖掘方法，其基本预测过程是采用最小化的结构风险准则，通过非线性映射函数将输入信息向高维空间进行映射，建立起输入信息与输出信息间的关系，能有效解决非线性的预测问题，具有运算速度快、精度高等优点。

在支持向量机的应用过程中，首先引入超平面的概念，它指的是输入信息与输出信息在数量关系上的回归线。支持向量机一元线性回归的超平面可表示为

y=b+wx[9]。

(1)

式中： y为输出信息； b为截距； w为斜率； x为输入信息。

二元线性回归的超平面则可表示为

y=b+w1x1+w2x2。

(2)

进一步可将n个输入变量的超平面表示为

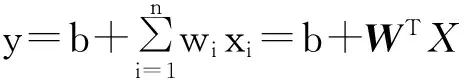
(3)

式(3)中的W为斜率向量，可表示为

WT={w1,w2,…,wn}。

(4)

同时，由于在n维空间中可能找不到较为合适的超平面，可利用核函数将样本间接地映射到高维空间，而核函数有若干形式，如多项式、线性、径向基及Sigmoid。结合实例特点，将核函数选定为Sigmoid函数。在支持向量机的应用过程中，利用损失函数对平面参数进行估计，采用的损失函数为ε(不敏感损失函数)，且在输入变量较多的情况下，ε(不敏感损失函数)会呈现“管道”现象。“管道”内的点误差可忽略，外侧的点即为支持向量。

可将支持向量机的目标函数定义为

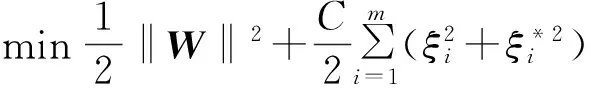
(5)

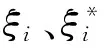
在式(5)的应用过程中，需满足的约束条件如下：

(b+WTXi)-yi≤ε+ξi(i=1,2,…,m)；

(6)

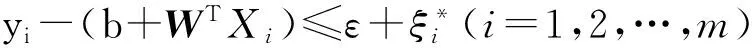
(7)

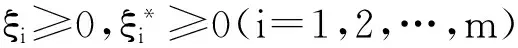
在支持向量机的预测过程中，采用滚动预测的思想，以提高预测结果的准确性[9]。滚动预测思想认为预测节点xi的变形值与前n个节点相关，因此将序列{x0,x1,…,xn-1}作为输入，以xn为输出，以此类推进行训练； 而在验证或预测样本中，将预测值替换为对应时间节点的值，且结合实例特点，将n值确定为10。该方法能将有限样本进行较好的推广预测，是一种较好的非线性识别方法。

1.2 BP神经网络

BP神经网络是一种多层前馈神经网络，具有较强的非线性映射能力，结构图如图1所示。

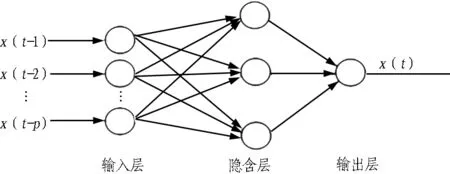
图1 BP神经网络结构图

在BP神经网络的参数设定过程中，选定train函数为训练函数，学习率设定为0.2，节点的连接权值区间设定为(0,1)，期望精度为0.01，最大迭代次数为 1 000次。同时，隐层节点数对预测精度及收敛速度具有较大的影响，结合文献[10]的研究，采用试算法确定最优隐层节点数，试算区间为5～12。

将BP神经网络的预测流程[11]分述如下：

1)根据网络结构的设定，对各节点的权值进行初始化赋值。

2)根据训练样本进行训练，得到输出值Tk′。

3)若输出值满足期望要求，则停止训练；若不满足期望要求，则采用梯度法进行权值修正，且将输出误差的函数表示为

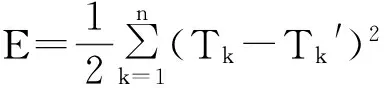
(8)

权值修正函数表示为

wij′=wij+Δwij=wij+ηδqi。

(9)

式(8)—(9)中：Tk为输出目标值；wij为原有权值；wij′为修正权值；η为学习因子；δqi为误差修正系数。

4)在规定最大迭代次数内，若训练误差达到收敛误差，则停止迭代；若未达到收敛误差，则输出最后预测，并对模型参数进行重新设定，再重复进行训练，直到误差达到收敛误差。

同时，本文BP神经网络结构采用的是递推模型结构，是将xi节点的前n个节点的变形值作为输入样本，且n值设定为10。该模型具有滚动预测的特点，推广性较强。

1.3 R/S分析

R/S分析首先由Hurst将其应用于尼罗河的水文分析中，可对时间序列的长期相关性及分形特征进行判断，进而确定时间序列的趋势项。

若将隧道的时间序列表示为{Ni}(i=1,2,…,N)，将其划分为A个长为n的子序列，设定每个子序列为Ia(a=1,2,…,A)，且子序列中的每个元素可表示为Nk,a，则子序列Ia的平均值可表示为

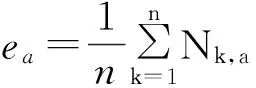
(10)

式中ea为子序列的均值。

根据子序列的基本元素和均值，计算各子序列的累计离差，即

(11)

进一步计算得到每个子序列的极差

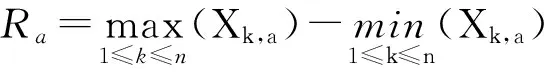
(12)

同时，每个子序列的标准差为

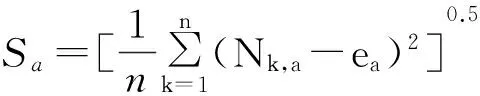
(13)

经过前述对极差和标准差的求解，可得到各子序列的重标度极差为

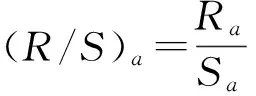
(14)

对于特定n值时，可将其重标度极差的均值表示为

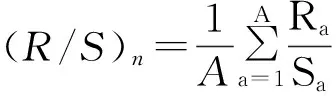
(15)

当n值不同时，可得到多个(n，(R/S)n)散点，且根据Mandelbrot的研究成果，lgn和lg (R/S)n之间存在线性关系如下。

lg (R/S)n=lgC+H·lgn。

(16)

式中：H为Hurst值；C为常数。

根据Matlab的cftool工具箱对若干(n，(R/S)n)节点进行最小二乘拟合，以得到Hurst指数，进而判断隧道的变形趋势。

1.4 预测步骤

预测模型的预测步骤分述如下：

1)利用小波去噪和卡尔曼滤波对基坑变形的原始序列进行去噪处理，并探讨小波分解层数及小波函数对去噪效果的影响；同时，以信噪比和均方根误差为基础指标，以其归一化值累加作为综合评价指标，对比筛选出最优去噪结果，将其作为趋势项和误差项的分离依据。

2)利用支持向量机和BP神经网络分别对趋势项和误差项进行预测，并将两者的结果进行叠加，即得到基坑变形预测的综合结果；将预测结果与文献[12]的预测结果进行对比，以验证预测思路的有效性。

3)利用重标度极差分析(R/S分析)对基坑变形的原始序列进行变形趋势判断，并将判断结果与预测结果进行对比分析，相互验证各自的准确性。

预测步骤集合了多种方法的优点，将其进行结构组合，以增强预测模型的稳定性，同时利用R/S分析法对预测结果进行验证，进一步核实了预测模型的有效性，为基坑变形预测提供了一种新的预测思路。另外，由于小波去噪[7]、卡尔曼滤波[13]及R/S分析[10]已在相关文献中进行了详细的原理介绍，这里不再赘述。

2 实例分析

2.1 工程概况

某基坑[12]开挖深度较大，最大深度达32 m，其所处的地貌多以山间冲积洼地和剥蚀残丘为主，地形起伏变化较小，相对高差为6.75 m。上覆土层主要是第四系覆盖层，以人工填土、冲洪积层和残积土层为主，下覆岩层为侵入岩，岩性为花岗岩。基坑地下水位受地形及降雨的影响较大，埋深在1.9～6.5 m，以孔隙潜水和基岩微承压水为主。同时，基坑所处区域的地质问题较多，如软土震陷、砂土液化等，在施工扰动的作用下，易使土层结构遭到破坏，进而导致土体压缩变形，影响基坑的稳定，也易诱发邻近建筑物的变形破坏。因此，基坑开挖过程中的施工监测就显得格外重要，根据监测成果进行预测分析，能有效实现信息反馈，以达到指导施工的目的。预测以Z70监测点的沉降数据为例，共计110个周期，每周期为1周，其变形曲线如图2所示。

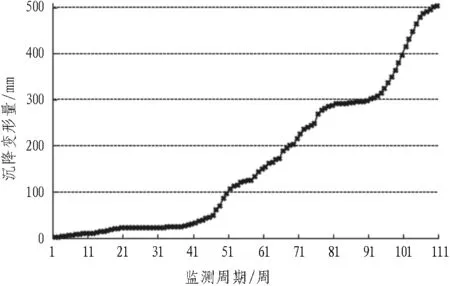
图2 基坑沉降变形曲线

由图2可得出： 基坑的沉降变形具有明显的阶段性特征，表现为“缓—陡—缓—陡”的趋势，最大变形量达504.2 mm； 其变化原因与施工阶段相关，且累计变形量大，说明变形预测研究的必要性强。

再对基坑的变形速率进行统计作图，见图3，得出基坑的沉降速率波动起伏较大，规律性较差，说明基坑变形受施工及环境因素的扰动较大，随机性和波动性较强，这也从侧面反映出基坑变形预测的困难，体现出对基坑变形综合研究的价值。基坑沉降变形速率的最大值和最小值分别为19.9 mm/周期和0.1 mm/周期，平均变形速率为4.58 mm/周期，说明基坑沉降变形波动较大。

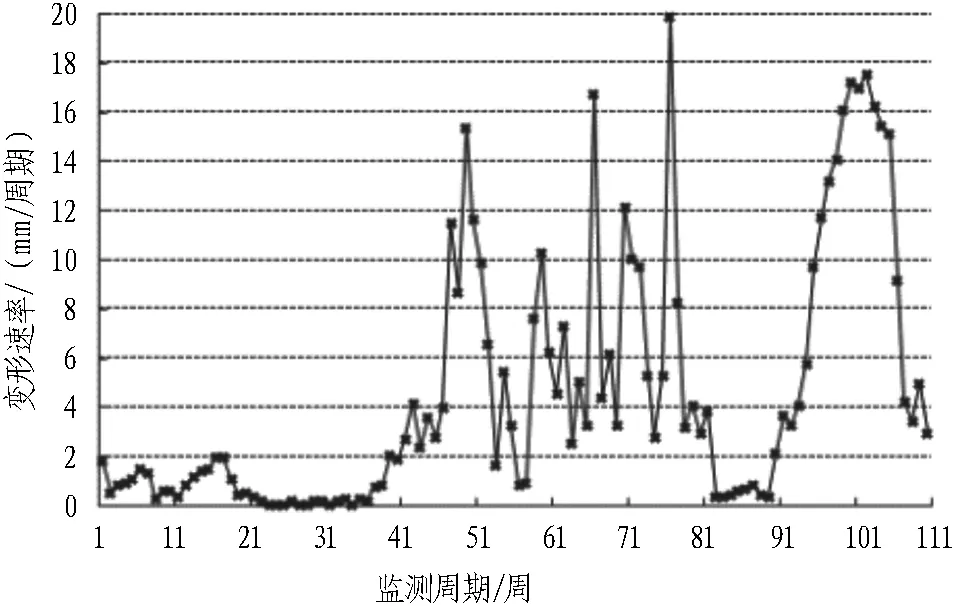
图3 基坑沉降速率变形曲线

2.2 去噪分析

采用小波去噪和卡尔曼滤波对基坑沉降的原始变形序列进行去噪处理。由文献[7]的研究，得到硬阈值方法和启发式阈值标准的去噪效果较好，因此，仅对小波分解层数及小波函数的去噪效果进行研究。其中，小波函数包含db小波系和sym小波系，分解层数分别为6、8、10、12、14层，小波系的去噪结果如表1和表2所示。

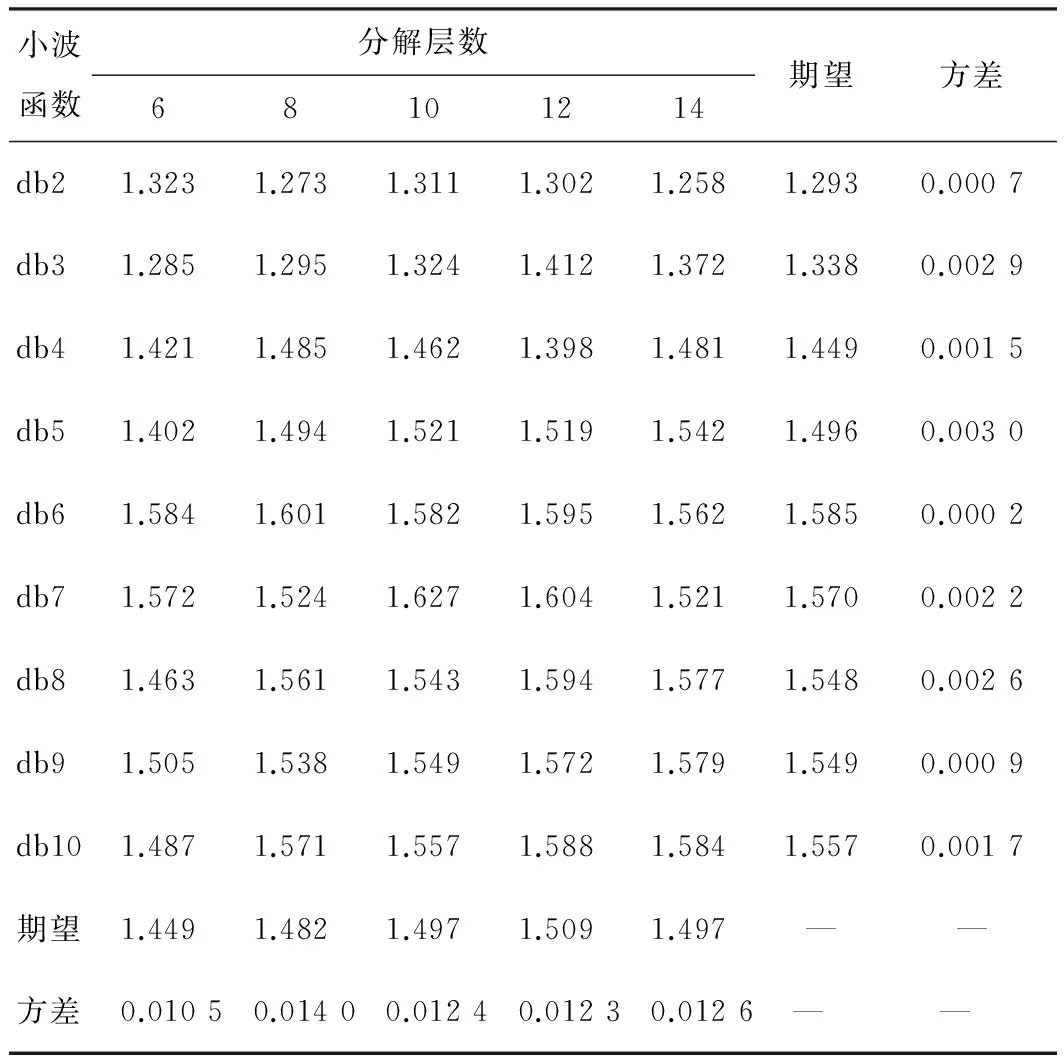
表1 db小波系去噪结果

在db小波系的去噪结果中，小波函数的阶次和分解层数对去噪效果均有较大的影响。其中： 随着分解层数的增加，去噪效果总体表现为先变优后变差的特点，以12层的去噪效果为最优，且去噪效果的稳定性变化差异不大；在小波阶次对去噪效果的影响方面，总体表现为随着阶次的增加，去噪效果相对更优，以第6阶次的去噪效果为最优。同时，在db小波系的所有去噪结果中，以db7小波函数在10层小波分解时的去噪效果为最优。

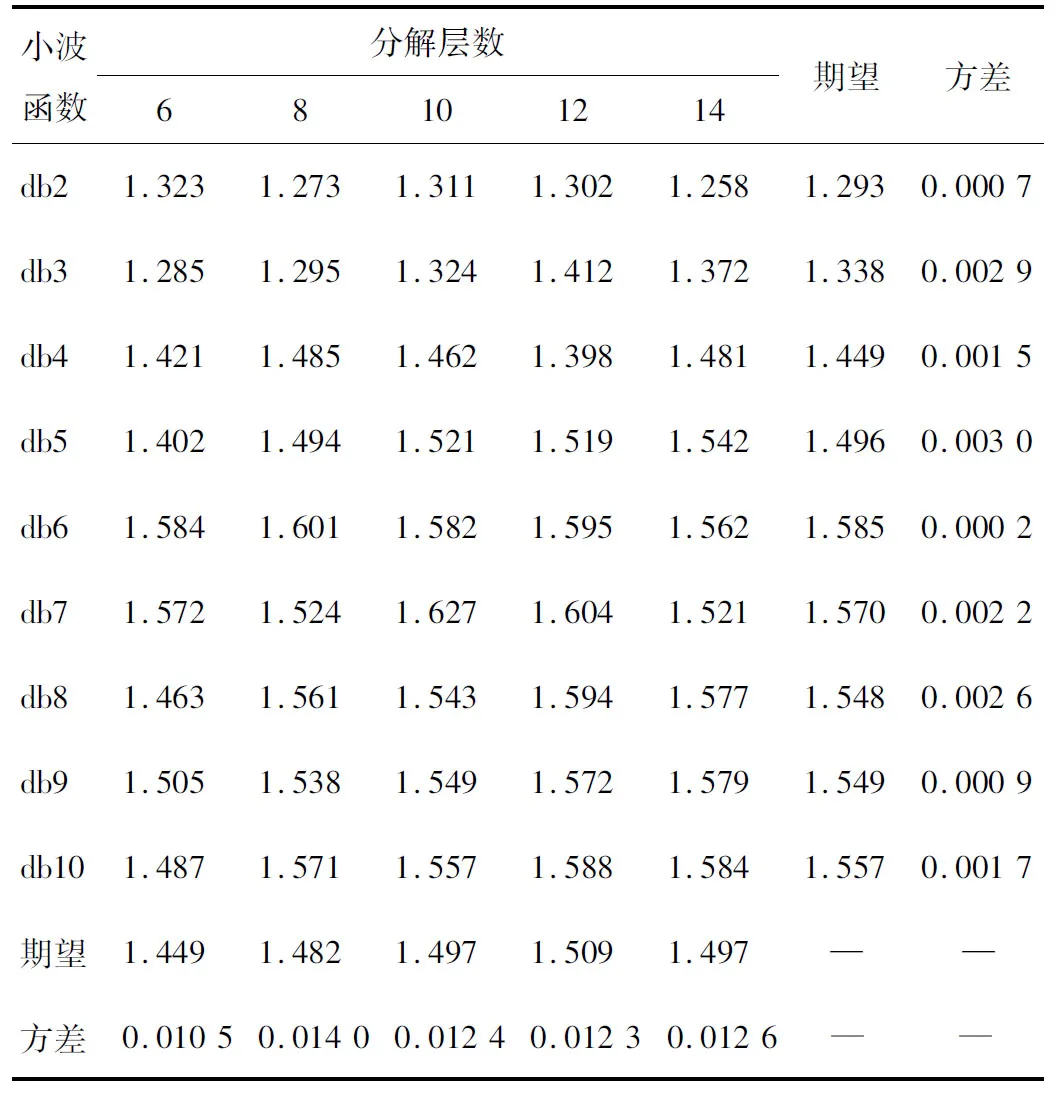
表2 sym小波系去噪结果

在sym小波系的去噪结果中，分解层数对去噪效果的影响规律与db小波系相同，只是最优分解层数为10层，而最优小波阶次则为第6阶次。同时，sym小波系的最优去噪结果是sym6小波函数在10层分解时的去噪结果。

为进一步对比2个小波系的去噪结果，再对2个小波系的去噪结果进行对比分析，如图4和图5所示。

图4 分解层数的影响对比

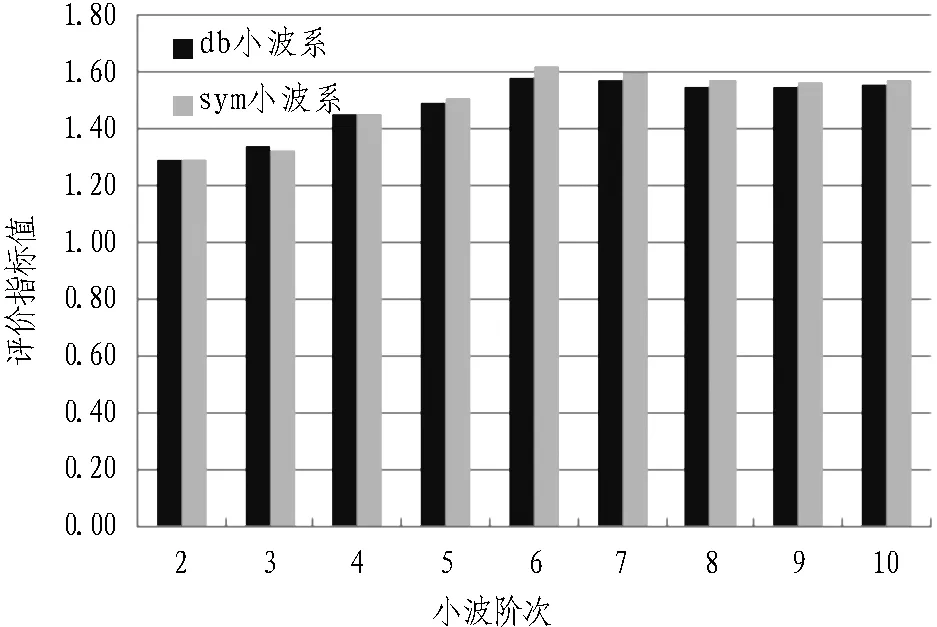
图5 小波阶次的影响对比

由图4可知： 6层、8层和10层的去噪效果均是sym小波系相对更优，且以6层的去噪效果差距最大；12层和14层的去噪效果以db小波系相对更优。说明sym小波系更适用于分解层数较少的情况，而db小波系更适用于分解层数较多的情况。

由图5可知，2个小波系均是随小波阶次的增加，去噪效果相对更优，且随着阶次的增加，sym小波系的去噪效果要优于db小波系的去噪效果，但差异均不大。说明小波阶次越高，去噪效果越好，但影响不大。

对比2个小波系的稳定性，得出分解层数去噪效果的稳定性以db小波系相对略优，而小波阶次去噪效果的稳定性则以sym小波系相对更优。最后，综合得到在小波去噪的结果中，以sym6小波函数在10层分解时的去噪效果为最优。

卡尔曼滤波的去噪结果如表3所示。由表3可知，自适应卡尔曼滤波的评价指标值为1.582，而半参数卡尔曼滤波的评价指标值为1.621，相对更优。

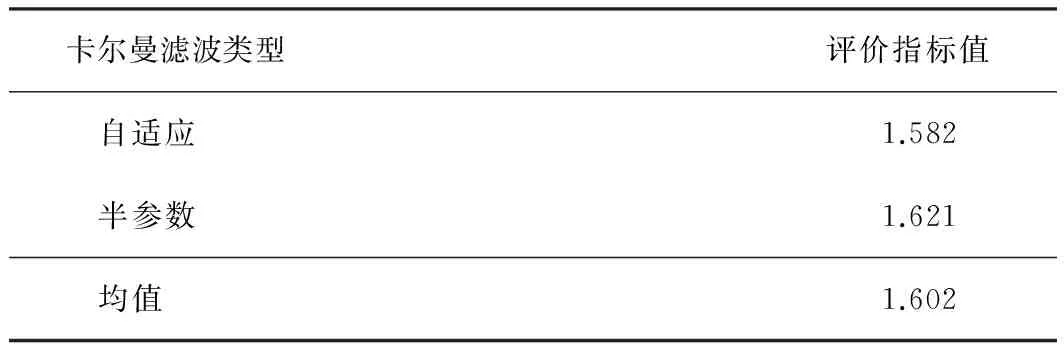
表3 卡尔曼滤波的去噪结果

对比小波去噪和卡尔曼滤波去噪的结果，得出不同去噪方法所能达到的效果也具有差异，就最优结果而言，以小波去噪的效果为最优； 因此，以sym6小波函数在10层分解时的结果作为趋势项和误差项序列的分离依据。

2.3 变形预测

采用支持向量机对趋势项序列进行预测，预测结果如表4所示。根据趋势项的预测结果，相对误差值均小于2%，其中，最大相对误差值为1.4%，最小相对误差值为0.8%，且相对误差平均值为1.07%，方差值为0.057 9，得出趋势项的预测精度及稳定性均较好，验证了支持向量机在趋势项预测中的有效性。

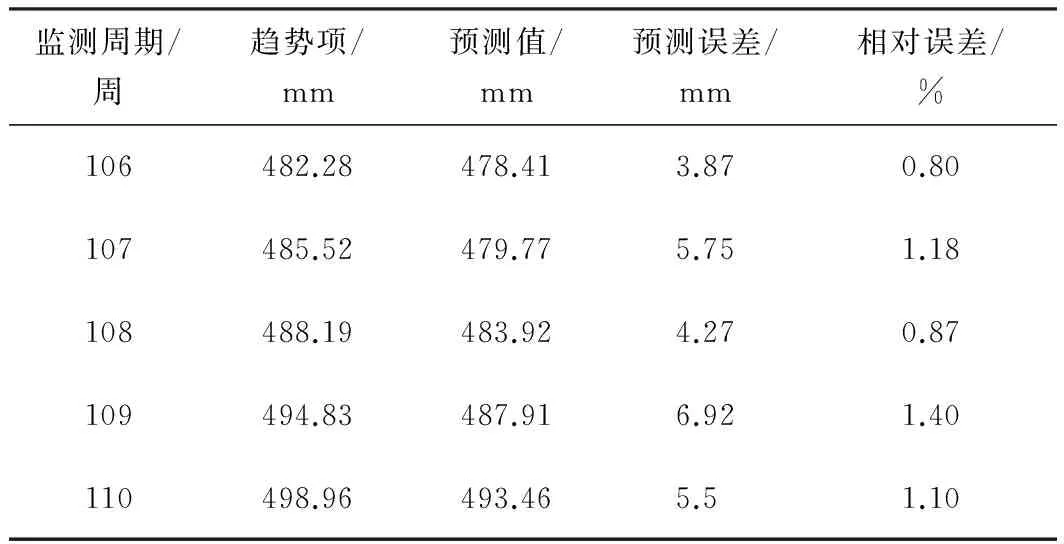
表4 趋势项预测结果

采用BP神经网络对趋势项序列进行预测，采用试算法对最优隐层节点进行试算，结果如表5所示。通过试算得出隐层节点数对预测效果的影响是存在的，说明采用试算法确定最优节点的方法是可行的。随着隐层节点数的增加，误差平方和表现为先减小后增大的规律，节点数为10时的误差平方和最小，值为1.713 7 mm2，且后期增加的幅度小于前期减小的幅度，说明最优节点数前的节点对预测精度的敏感性要大于最优节点数后的节点对预测精度的敏感性。综合试算结果，隐层节点确定为10，将该节点对应的预测结果作为误差项的预测结果。

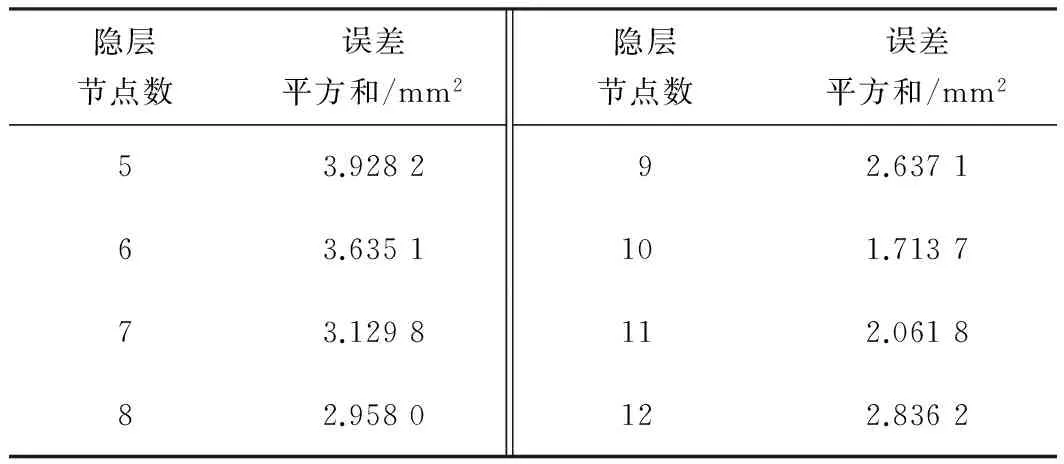
表5 隐层节点试算结果

误差项序列的预测结果如表6所示。在误差项的预测过程中，预测误差绝对值的最大值和最小值分别为0.7 mm和0.4 mm，且相对误差绝对值在6%～12%，得出误差项预测结果的特点总体表现为： 预测的绝对误差值小，但相对误差值大，与误差序列的随机性强相关。

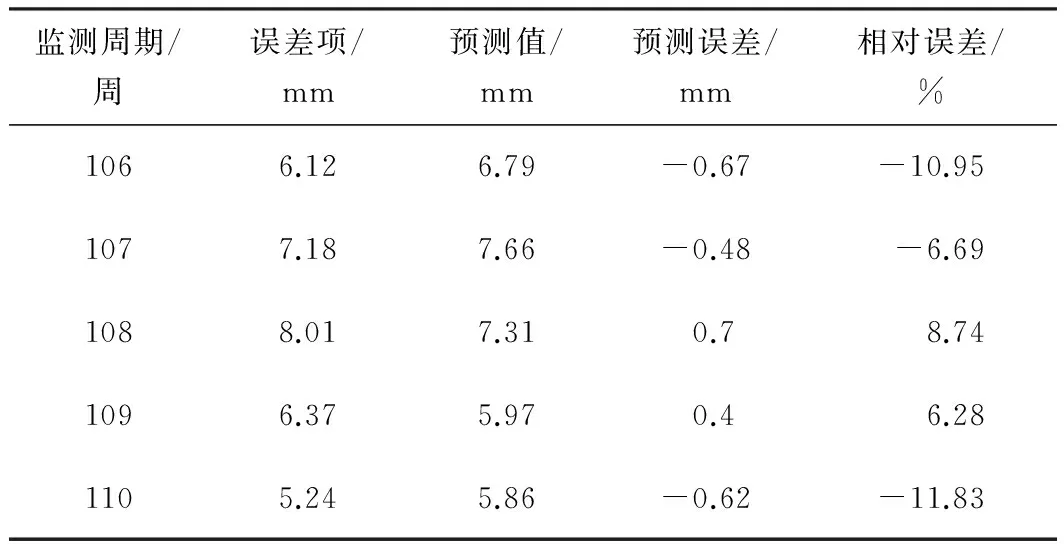
表6 误差项序列预测结果

对比趋势项和误差项的预测结果，在对应监测周期的相对误差值，均是误差项序列的值较大，且差异明显。说明趋势项序列的预测精度要明显高于误差项序列，这与误差项序列含有较多的误差因素有关，也从侧面反映出通过去噪处理分离趋势项和误差项的方法是可行的，达到了预期的效果和目的。

通过对趋势项和误差项的预测，将两者的结果进行叠加，得到基坑变形的预测结果如表7所示。得出预测结果相对误差的均值为1.03%，方差值为0.083，分离序列的预测精度及稳定性均有所提高。同时，为对比预测结果的有效性，将文献[12]中的预测结果一并进行统计，得到其相对误差均值为2.98%，最大相对误差达-7.27%，方差值为7.368 4，相对本文预测结果，预测精度或稳定性均较差，验证了本文预测模型具有相对更好的优越性。另外，对最后3个周期进行递推预测，得出基坑在后3个周期的变形仍呈增长趋势，最大变形预测值已达516.01 mm。

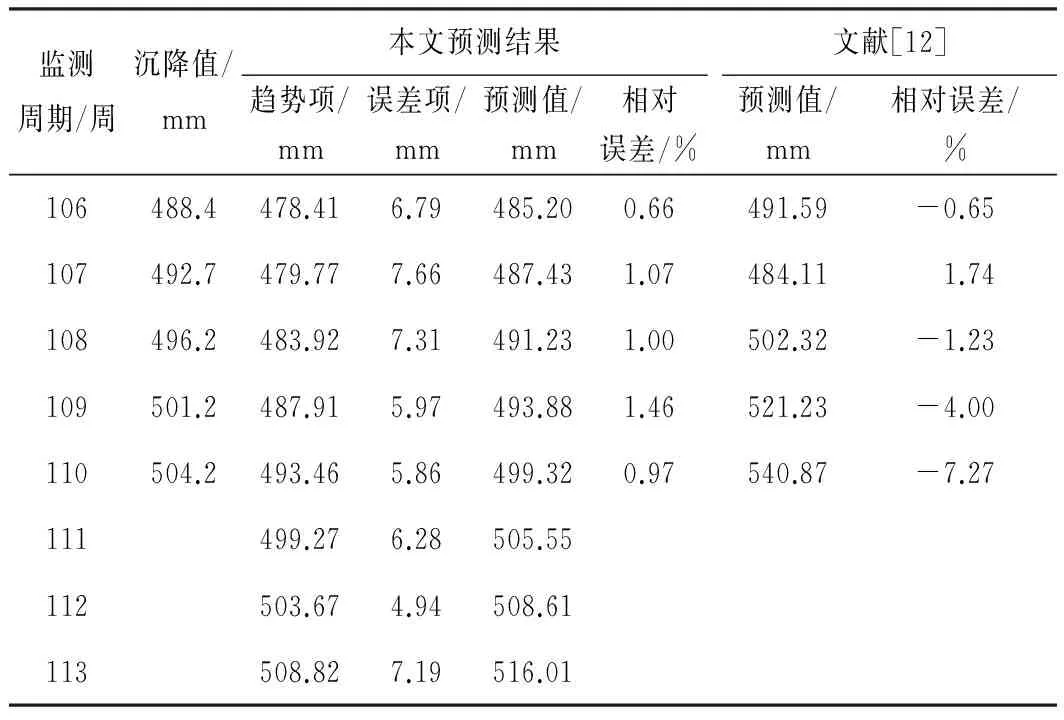
表7 基坑变形预测结果

2.4 变形趋势判断

为进一步判断基坑的变形趋势及验证前文预测结果的可信度，采用R/S分析对基坑变形的变形序列和速率序列进行重标度极差分析，分析数据来源于基坑变形的实测数据，即前110周期的变形数据。经过计算得到分析结果如表8所示。

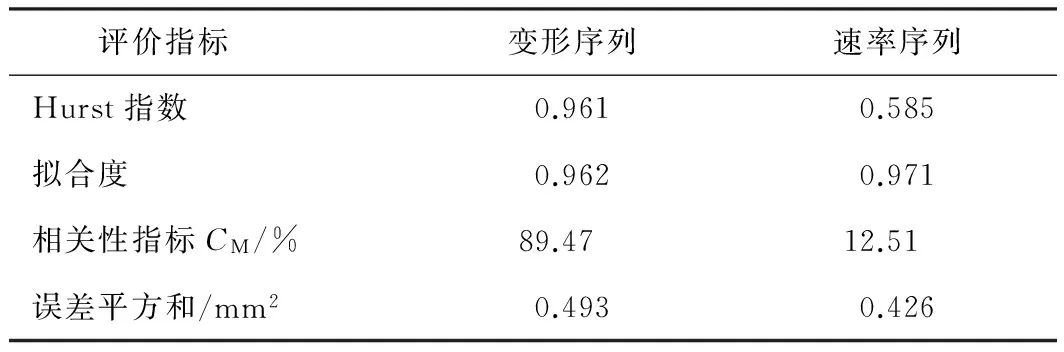
表8 R/S分析结果统计

由表8可知： 变形序列的Hurst指数值为0.961，速率序列的Hurst指数值为0.585，均大于0.5。说明2个序列均具有长期的记忆性和持续性，是持续增强序列，基坑的变形将会继续增加，这与基坑的变形预测结果一致，验证了前期预测模型的准确性； 但变形序列较速率序列的Hurst指数值要大，且速率序列的Hurst指数值接近0.5，说明变形序列的趋势性较速率序列强，而速率序列相对具有更强的随机性。2个序列的拟合度均较为接近1，误差平方和也较小，说明重标度极差分析结果的可信度较高，其中速率序列的拟合度略高于变形序列的拟合度。2个序列的相关性指标CM均大于0，得出2个序列均为正相关，且变形序列的相关性程度明显高于速率序列。

综合对比变形预测及趋势判断的结果，得出基坑的变形具有持续增长的趋势，需要加强现场监测，并采取必要的控制变形措施。

3 结论与讨论

1)通过小波去噪能很好地剔除误差信息，分离趋势项及误差项，但不同的去噪参数对去噪效果的影响较大，通过试算法确定最优去噪参数的可行性较好。在去噪分析过程中，sym小波系的去噪效果要优于db小波系的去噪效果，而分解层数的去噪效果主要表现为随分解层数的增加去噪效果先变优后变差，存在最优分解层数。

2)对比趋势项和误差项序列的预测结果，得出趋势项的预测精度及稳定性均明显高于误差项的预测精度及稳定性，这是由于误差序列含有更多的误差因素所致，也从侧面反映出去噪处理的有效性。

综上所述，通过建立综合预测模型进行基坑的变形预测，并通过重标度极差分析方法对变形趋势进行判断，能进一步验证变形预测的可靠性，可为基坑的变形及稳定性评价提供一种新的思路。

[1] 王宁伟, 朱丰, 韩旭, 等. 基于小波去噪的灰色马尔柯夫基坑变形预测[J]. 水利与建筑工程学报, 2015(4): 215. WANG Ningwei, ZHU Feng, HAN Xu, et al. The deformation prediction of deep foundation pits based on a wavelet denoised grey Markov Model [J]. Journal of Water Resources and Architectural Engineering, 2015 (4): 215.

[2] 张世豪, 朱德华. 基于BP神经网络的深基坑变形预测[J]. 南京工程学院学报(自然科学版), 2016, 14(3): 17. ZHANG Shihao, ZHU Dehua. Deformation prediction of deep foundation pits based on BP neural network [J]. Journal of Nanjing Institute of Technology (Natural Science Edition), 2016, 14 (3): 17.

[3] 吴欢, 周春波, 秦昆. 基于改进支持向量机的深基坑变形预测[J]. 地矿测绘, 2015, 31(4): 25. WU Huan, ZHOU Chunbo, QIN Kun. Deformation prediction of deep foundation pit based on improved support vector machine[J]. Surveying and Mapping of Geology and Mineral Resources, 2015, 31 (4): 25.

[4] 渠孟飞,谢强,李朝阳,等. 基于支持向量机的膨胀土深基坑变形预测研究[J]. 施工技术,2016,45(19): 30. QU Mengfei， XIE Qiang, LI Zhaoyang, et al. Prediction of slope displacement of deep foundation excavation based on support vector machine [J]. Construction Technology，2016, 45(19): 30.

[5] 林楠, 李伟东, 张文春, 等. 最小二乘支持向量机在深基坑变形预测中的应用[J]. 辽宁工程技术大学学报, 2014(11): 1471. LIN Nan, LI Weidong, ZHANG Wenchun, et al. Application of least squares support vector machine to deformation prediction of deep foundation pit [J]. Journal of Liaoning Technical University, 2014 (11): 1471.

[6] 曾晖, 胡俊, 鲍俊安. 基于BP人工神经网络的基坑围护结构变形预测方法研究[J]. 铁道建筑, 2011(1): 70. ZENG Hui, HU Jun, BAO Jun′an. Study of prediction method of deformation of foundation pit enclosure-structure based on BP (error back-propagation) artificial nerve network [J]. Railway Engineering, 2011 (1): 70.

[7] 杨哲峰, 罗林, 贾东彦, 等. 基于小波去噪的深基坑变形预测研究[J]. 人民长江, 2014(19): 41. YANG Zhefeng, LUO Lin, JIA Dongyan, et al. Prediction of deep foundation pit deformation based on wavelet denoising [J]. Yangtze River, 2014 (19): 41.

[8] 庞建成, 隆然, 马娇. 基于改进R/S分析方法的深基坑变形预报预测研究[J]. 施工技术, 2015, 44(13): 56. PANG Jiancheng, LONG Ran, MA Jiao. Study of deformation prediction of deep foundation pit based on improved R/S analysis [J]. Construction Technology, 2015, 44 (13): 56.

[9] 师旭超, 梁醒培. 深基坑变形预测的进化支持向量机模型[J]. 武汉理工大学学报, 2010(1): 158. SHI Xuchao, LIANG Xingpei. An evolutionary support vector machine model for deformation prediction of deep foundation pit [J]. Journal of Wuhan University of Technology, 2010 (1): 158.

[10] 罗林, 左昌群, 赵连, 等. 基于BP神经网络和R/S分析的隧道仰坡沉降变形预报预测[J]. 施工技术, 2014(11): 80. LUO Lin, ZUO Changqun, ZHAO Lian, et al. Prediction of settlement deformation of tunnel on the basis of BP neural network and R/S analysis [J]. Construction Technology, 2014 (11): 80.

[11] 龙浩, 高睿, 孔德新,等. 基于BP神经网络-马尔科夫链模型的隧道围岩位移预测[J]. 长江科学院院报, 2013, 30(3): 40. LONG Hao, GAO Rui, KONG Dexin, et al. Forecast of tunnel′s surrounding rock displacement by BP neural network and Markov Chain [J]. Journal of Yangtze River Scientific Research Institute, 2013, 30 (3): 40.

[12] 黄传胜. 地铁深基坑开挖变形预测方法及工程应用研究[D]. 长沙： 中南大学, 2011. HUANG Chuansheng. Study of deformation prediction method and engineering application of deep foundation pit excavation [D]. Changsha： Central South University, 2011.

[13] 王成, 何美琳, 覃婕,等. 半参数Kalman滤波模型在GPS变形数据处理中的应用[J]. 施工技术, 2015(增刊2)： 831. WANG Cheng, HE Meilin, QIN Jie, et al. Semiparametric Kalman filtering model in the application of GPS data processing of deformation [J]. Construction Technology, 2015 (S2): 831.

Study of Application of Trend Term Separation Prediction Model and Rescaled Range (R/S) Analysis to Deformation Prediction of Deep Foundation Pit

WANG Xueni1, HAN Guofeng2

(1.YanglingVocational&TechnicalCollege,Xianyang712100,Shaanxi,China;2.ShaanxiRailwayInstitute,Weinan714000,Shaanxi,China)

The deformation prediction accuracy of foundation pit is low nowadays. The denoising is carried out for deformation sequence of foundation pit by wavelet denoising and Calman filter, the trend term and error term are separated, and the trend term and error term is predicted by support vector machine (SVM) and BP neural network respectively. Meanwhile, the deformation trend of foundation pit is predicted by rescaled range (R/S) analysis so as to verify the feasibility of deformation prediction results. The case study shows that: 1) For wavelet denoising method, the denoising effect is superior; the average relative error and variance of the prediction results is 1.03% and 0.083 respectively; and the prediction accuracy is much higher. 2) The deformation sequence and deformation velocity sequence of foundation pit are prone to increasing, which coincide with the prediction results and verify the effectiveness of the prediction idea.

deep foundation pit; deformation prediction; denoising analysis; support vector machine (SVM); rescaled range (R/S) analysis; trend judgment

2017-01-04;

2017-04-24

王雪妮(1984—)，女，陕西富平人，2011年毕业于西安建筑科技大学，安全技术及工程专业，硕士，讲师，主要从事建筑施工及安全管理工作。E-mail: 568756588@qq.com。

10.3973/j.issn.1672-741X.2017.08.012

U 452.1+1

A

1672-741X(2017)08-0990-07