基于海明距离-TOPSIS法的山区公路隧道扩建方案直觉模糊优选

邬晓光， 贺 攀，*， 苏兴矩， 钱若霖

(1. 长安大学桥梁与隧道陕西省重点试验室， 陕西 西安 710064； 2. 长安大学公路学院， 陕西 西安 710064;3. 福建厦蓉高速公路漳龙段扩建工程有限公司， 福建 龙岩 364000)

基于海明距离-TOPSIS法的山区公路隧道扩建方案直觉模糊优选

邬晓光1, 2， 贺 攀1, 2，*， 苏兴矩3， 钱若霖1, 2

(1. 长安大学桥梁与隧道陕西省重点试验室， 陕西 西安 710064； 2. 长安大学公路学院， 陕西 西安 710064;3. 福建厦蓉高速公路漳龙段扩建工程有限公司， 福建 龙岩 364000)

为了解决山区高速公路隧道改扩建方案选取决策困难而又缺乏理论依据的问题，基于直觉模糊数的海明距离，结合TOPSIS方法，增加专家权向量修正，进而得到处理具有优先级别关系的多属性问题的决策方法。分析山区高速公路隧道改扩建的影响因素，建立隧道扩建方案影响指标体系。从依托工程实际出发，邀请指定的专家对指标优先级别排序，然后利用已建的数学模型实现扩建方案寻优。该方法在厦蓉高速公路隧道改扩建施工方案优选中得到有效运用，说明该方法实用可行，对隧道改扩建施工方案以及类似工程方案优选问题具有重要的指导意义。

厦蓉高速公路； 山区； 隧道改扩建； 海明距离； 直觉模糊集

0 引言

在我国东南部山区，隧道的运输能力已成为经济发展的瓶颈，高速公路隧道的扩建极为迫切[1]。隧道的改建可以原位扩建，也可在既有隧道旁新建[2]。由于山区地形复杂，受路线线型的制约，原位扩建的施工方案成为一种优先考虑的形式。高速公路改扩建是一个复杂的系统工程[3]，影响隧道扩建施工方案的因素很多，有些因素能定量描述，有些却只能定性比较[4]，隧道的合理扩建是高速公路改扩建工程中的重点。选择合理的隧道改建方案显得至关重要，决策者要站在科学的角度，抓住问题要害，解决这些不确定性所带来的困难，制定出合理的施工方案[5]。在隧道改扩建施工方案选取时，决策者缺乏实用并且易于掌握的评价方法，致使方案选择缺乏科学依据，存在选择不合理的风险，故需要建立合理的评价体系，使用实用简单的方法进行隧道改扩建方案的优选。

现有方案优选评价的方法较多，总结起来都是对评价指标进行定性或定量相结合，按照相应的数学模型进行分析计算，得出方案优选排序。美国运筹学家萨蒂最早提出层次分析法，如将AHP法用于岩溶隧道突水突泥风险评估中[6]；现在学者多将层次分析法与模糊综合评价法相结合用于方案优选[7]，此种方法虽较为成熟，但权重的确定过于主观导致结果不能使人信服；采用德尔菲法[8]的专家评估法虽强调专家反复的无障碍决策，但过程中缺少信息交流，容易导致信息传递不对称；价值工程法[9]针对性较强，但过分强调功能经济，指标难以定量化处理；虽已有学者应用三角模糊-TOPSIS法数学模型对高铁隧道施工方案等工程方案进行优选[10-11]，但当涉及多属性、多群体专家决策时，过程繁琐，计算量太过庞大，工程决策人员一般较难掌握。

本文拟采用海明距离-TOPSIS直觉模糊数法进行隧道改扩建施工方案优选，其优点有： 1)隧道改扩建方案的选取是一个多属性的工程问题，并且带有很强的模糊和不确定性，各属性之间具有优先级别关系，此方法更加适用； 2)本文分析过程中增加专家权重分配，避免了个体主观和偶然性； 3)该方法运算量较小，易于掌握，并且在隧道改建等工程方案决策领域未见应用，可以为其他工程问题的决策提供参考。

1 山区高速公路隧道改扩建方案

1.1 高速公路隧道改扩建方案分类

从国内外高速公路隧道的改扩建工程施工方案选择中可以发现，总体上，从原有4车道隧道改建成8车道隧道的改扩建型式主要有3类[2,12]。

1)在原隧道周围新建2条单洞隧道，形成4洞8车道隧道群，如图1所示。

图1 新建独立双洞隧道

2)在原有隧道位置原位扩建形成双洞8车道隧道，如图2所示。

3)组合式扩建施工，即其中一个隧道采用原位扩建，另一个采用在既有隧道旁新增单洞双车道，如图3所示。

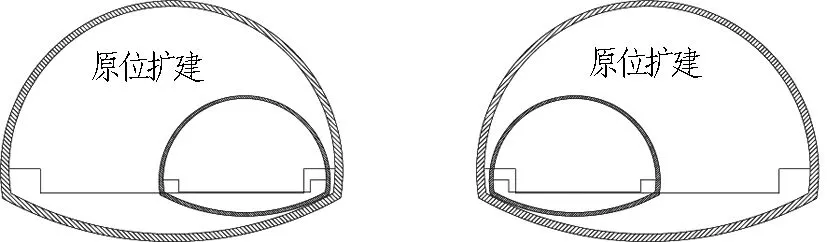
图2 双侧原位扩建隧道

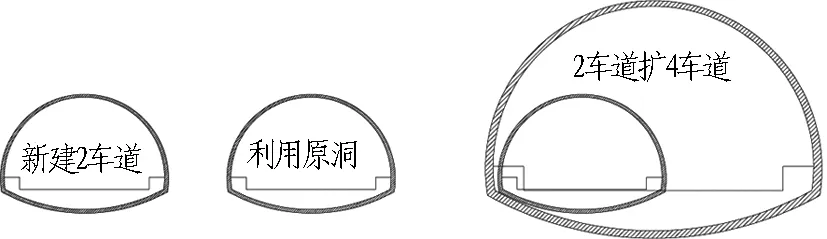
图3 组合式扩建开挖隧道

1.2 高速公路隧道改扩建方案的特点

1.2.1 新建独立双洞隧道

采用新建独立双洞隧道的扩建方案，与新建隧道的施工方法相同，对施工单位的施工技术水平要求不高；可边通车边施工；对线路改动小，对空间要求低，道路直顺性好[2]。但由于在既有隧道两侧或中间新建隧道，使得4条隧道之间的距离变小，易形成小净距隧道群。山区高速公路隧道采用钻爆法施工时，必须严格控制爆破振速，避免对原隧道造成影响[13-14]。除此之外，小净距隧道的布置受到地形的限制，在狭小的地段此种方案无法实现。

1.2.2 双侧原位扩建隧道

原位扩建隧道的最大特点是需要对原有隧道的衬砌和支护结构进行完全拆除[2]。部分隧道原位扩建时还需要对拱腔进行回填，避免对围岩造成过大的扰动。除此之外，开挖过程中围岩应力变化复杂，开挖之前需经详细的有限元计算分析。为保证过往车辆的通行，左右两侧隧道不能同时进行扩建，从而大大增加了施工工期。原位扩建虽施工难度大，但由于既有隧道位于扩建隧道内，原隧道作为隧道掘进爆破中的临空面，使得爆破的面积较新建隧道减少[3]。

1.2.3 组合式扩建开挖隧道

组合式扩建方式其实是为避免双洞开挖，形成小净距隧道以及减小原位扩建的施工难度，结合前2种开挖方案而形成的新的开挖形式。组合式开挖中原位扩建隧道仍具有较大的施工难度，但新建双车道隧道施工难度相对较小；并且这种开挖形式可以空出一条既有隧道，减少交通对施工的影响。

2 山区高速公路隧道改扩建评价指标的确定与分析

隧道在山区高速公路投资中占比较大。既有隧道的扩建不仅干扰过往车流，还有可能会对周围结构物造成影响，需选择合理的隧道扩建方案。本文重点从工程技术可行性、经济合理性、社会效益3方面，细化隧道改扩建评价指标，综合分析隧道改扩建方案的合理性。

2.1 工程技术可行性

评价隧道改扩建方案的关键因素是其技术的可行性，工程技术的可行性很大程度上决定了实施模式的选择。工程技术可行性不仅要考虑其施工难易程度，还要考虑不同的施工方法的可选择性，选择成熟、操作难度小的施工方法可以显著节约成本。施工过程中地质复杂多变，为保证隧道改建过程中的安全性，必须评估各种隧道开挖方法的风险性，提供必要的安全防护措施。对地质较差的施工山体段，小净距隧道需要严格控制爆破振速，防止诱发工程事故。

2.2 经济合理性

隧道改扩建与新建隧道不同，在考虑施工方案经济合理性时，除了设计到机械、人工、通风设备等成本消耗，还需要关注以下方面，进行综合权衡： 如隧道改扩建需要制订一整套可行的保畅方案。在不影响施工的基础上，还需要保证交通顺畅、行车安全，综合考虑每种方案所需要的交通保畅成本。既有隧道在开挖过程中，将会对相对稳定的围岩造成二次扰动，安全生产投入也会很大程度上增加；隧道的建设周期意味着资金的持续投入，综合选用建设周期短的扩建方案将会大大节省开支。

2.3 社会综合效益

高速公路作为一种公共产品，其在建设、运营过程中所产生的社会效益比起其作为交通运输重要组成部分所测定的经济效益要多得多[15]。隧道是其重要的组成部分，在建设过程中，应注重环境的保护，任何隧道扩建方案都不能以牺牲环境为代价。靠近村庄城镇时，还要考虑隧道施工对周围村镇的影响。大断面隧道内由于行车道数量较多，行车在隧道内机动性较大，多车道隧道需要考虑隧道内行车的安全性。任何一种施工方法的尝试和改进都会给隧道施工技术带来提升，隧道改扩建过程中需要总结施工经验，为国内其他地区隧道的施工提供指导。

2.4 山区高速公路隧道改扩建评价指标的建立

综合考虑隧道的地形、地质条件、行车要求、施工

技术水平及经济效益等因素，从工程技术可靠性、经济合理性和社会综合效益3方面考虑，建立山区高速公路隧道改扩建评价指标，如图4所示。

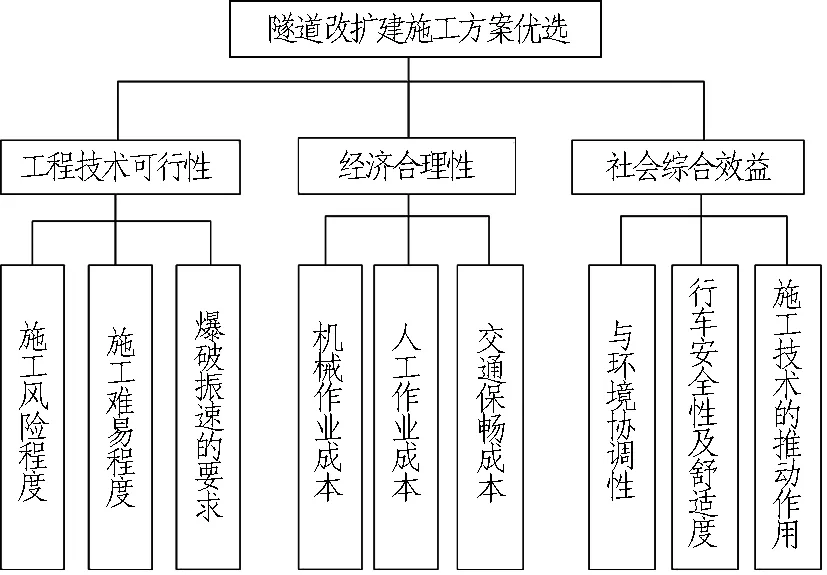
图4 山区高速公路隧道改扩建评价指标

Fig. 4 Evaluation indexes for rehabilitation of highway tunnels in mountain areas

3 基于海明距离-TOPSIS的厦蓉高速隧道扩建方案直觉模糊优选

3.1 厦蓉高速公路隧道改扩建施工方案指标综合分析

在建的厦蓉高速属于国家高速公路网中的东西横线，同时是海西高速公路网规划的第七横厦蓉线(G76)的重要组成部分。路线起于福建省漳州天宝，终于龙岩蛟洋。其中，漳州段推荐线拟设6座隧道，隧道区基岩岩性复杂，隧道进出口段围岩较差，土层厚度大，局部断裂构造段围岩较破碎，易产生坍塌现象，围岩稳定性差。其中，推荐K线仙岭隧道场区岩性以凝灰熔岩为主，场区构造发育，进口及洞身段有燕山晚期花岗岩出露，局部有中基性岩脉倾入，岩性较为复杂，构造带及岩性接触带围岩较差，围岩级别较低。龙岩段推荐线拟设12座隧道，各隧道围岩以粉细砂岩、砂砾岩、花岗(闪长)岩等为主，岩性变化较大，隧道工程地质条件一般。其中京源口隧道右线更是穿行于灰岩采空区附近，存在较大风险。

根据2.4节建立的指标体系以及基于厦蓉高速实际工程地质条件，以漳州境内的仙岭隧道为例，对图4所列的评价指标进行综合分析，通过多部门专家组座谈，整理所收集的专家意见，如表1—3所示。

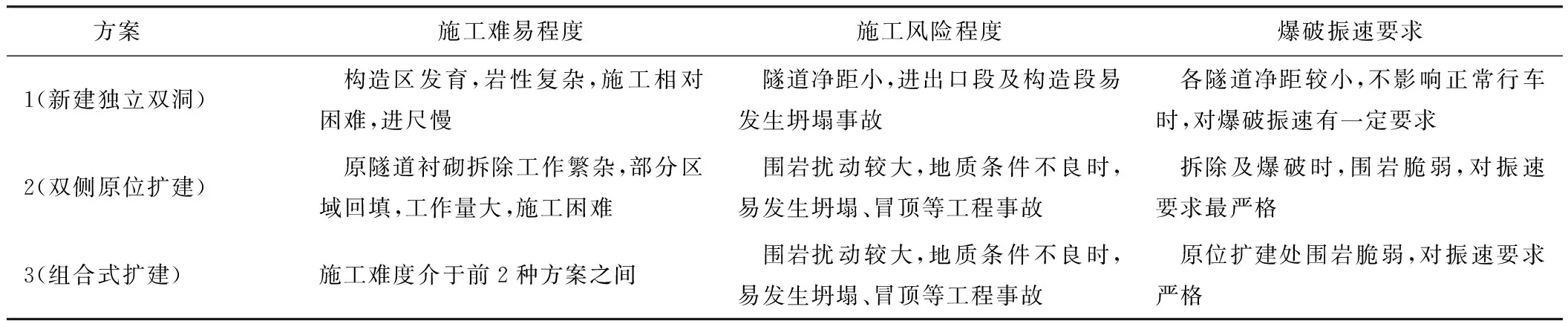
表1 工程技术可行性指标对比

表2 经济合理性指标对比

表3 社会综合效益指标对比

3.2 海明距离-TOPSIS直觉模糊数法模型的分析原理

1)参考已有理论研究[16-18]，建立海明距离-TOPSIS直觉模糊数法模型。对于一个多属性决策问题，假设实施方案共有m个，则方案集合为F={F1,F2，…，Fm}，评价指标集合为U={U1,U2，…，Un}，并且各指标间具有优先级别，假定U1>U2>…>Un。方案Fi在指标Uj下的值称为直觉模糊数，用αij=(μij,νij)表示，取值满足0≤μij,νij≤1且μij+νij≤1。其中，μij、νij分别代表方案Fi对指标Uj的隶属度、非隶属度，也即满足程度。

2)建立专家集合为E={E1,E2，…，Ek}，专家权向量为W=(w1,w2，…，wk)，通过专家调研得到其对评选方案fi在各评价指标uj下的取值，即αij，利用专家权向量，得到修正的直觉模糊数

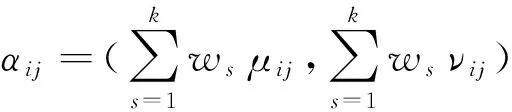
(1)

3)由标准海明距离的定义[19]，可计算任意一个α=(μ,ν)与最大直觉模糊数α+=(1,0)和最小模糊数α-=(0,1)的标准海明距离d+和d-。

d+=d(α,α+)=1-μ；d-=d(α,α-)=1-ν。

(2)

4)基于TOPSIS的原理，引入贴近度概念[18]，计算αij相对于最大直觉模糊数α+的相对贴近度，作为αij的得分。

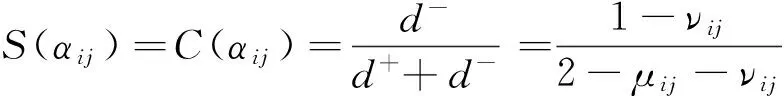
(3)

5)利用直觉模糊优先加权平均(IFPWA)算子对所有的αij进行集结。

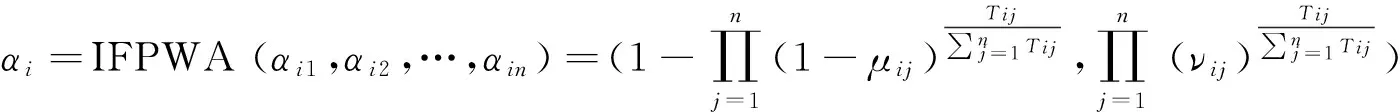
(4)

令Ti1=1 (i=1,2,…,m)；

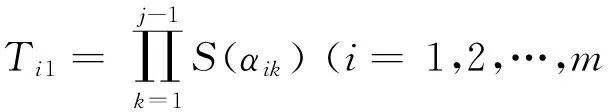
6)计算各备选方案集结结果αi(i=1,2,…,m)的贴近度，根据结果大小排序和优选。

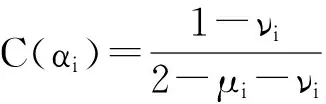
(5)

3.3 模型求解

依托厦蓉高速改扩建工程，成立“厦蓉高速漳州至龙岩段改扩建项目施工安全控制关键技术”研究课题组，参与仙岭隧道评分的6位专家由厦蓉高速管理处指定： 管理处高工2名、施工单位总工1名、环评部高工1名、交通工程领域教授1名及安全控制管理领域教授1名。根据隧道场区实际情况，评价指标的优先级程度也不尽相同，6位专家根据仙岭隧道现场实际，对指标集合进行了优先等级排序，其后根据方案对指标满意度的原则进行打分，由6位专家意见得到的原始直觉模糊数决策集合如表4—6所示。

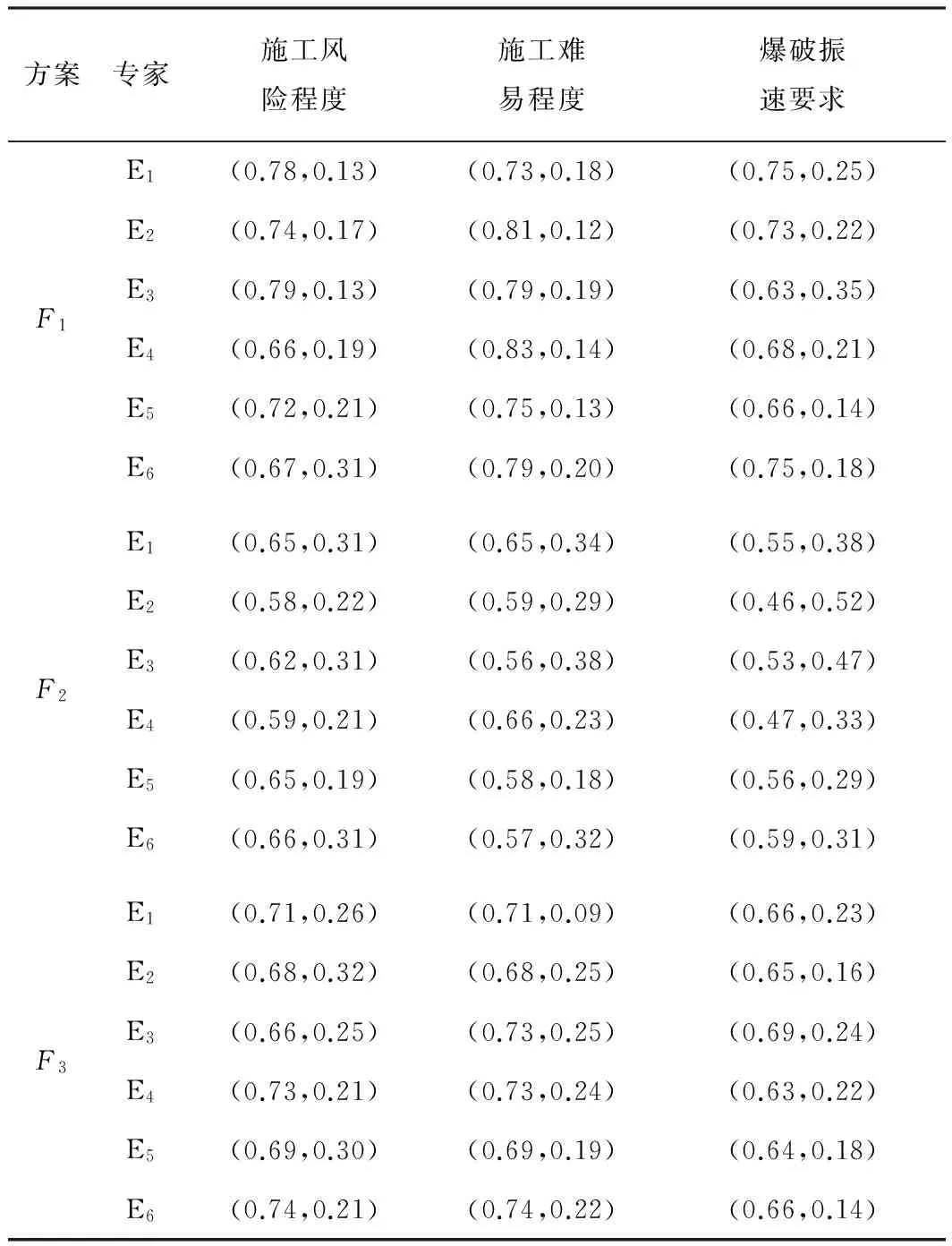
表4 工程技术可行性专家指标评分表

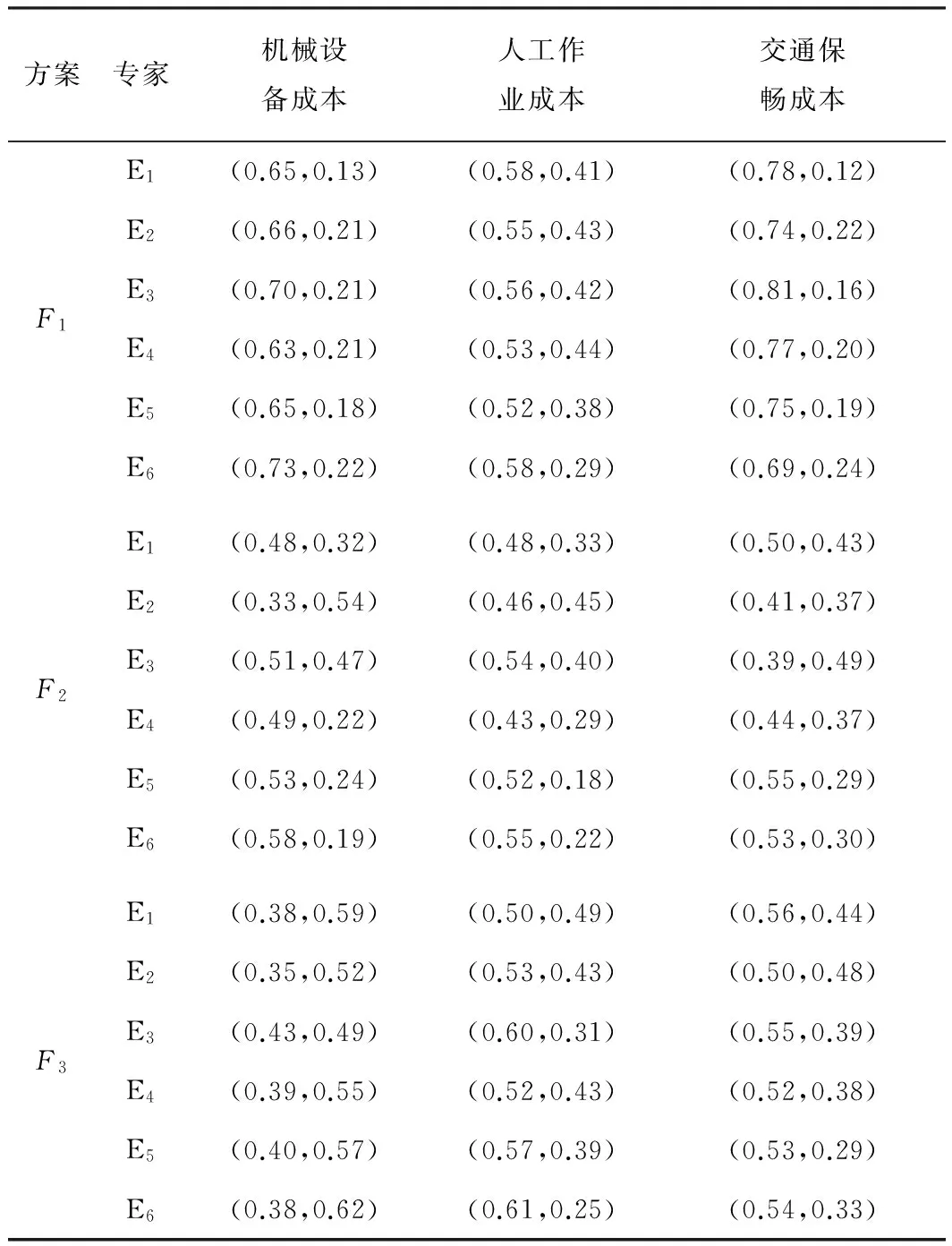
表5 经济合理性专家指标评分表

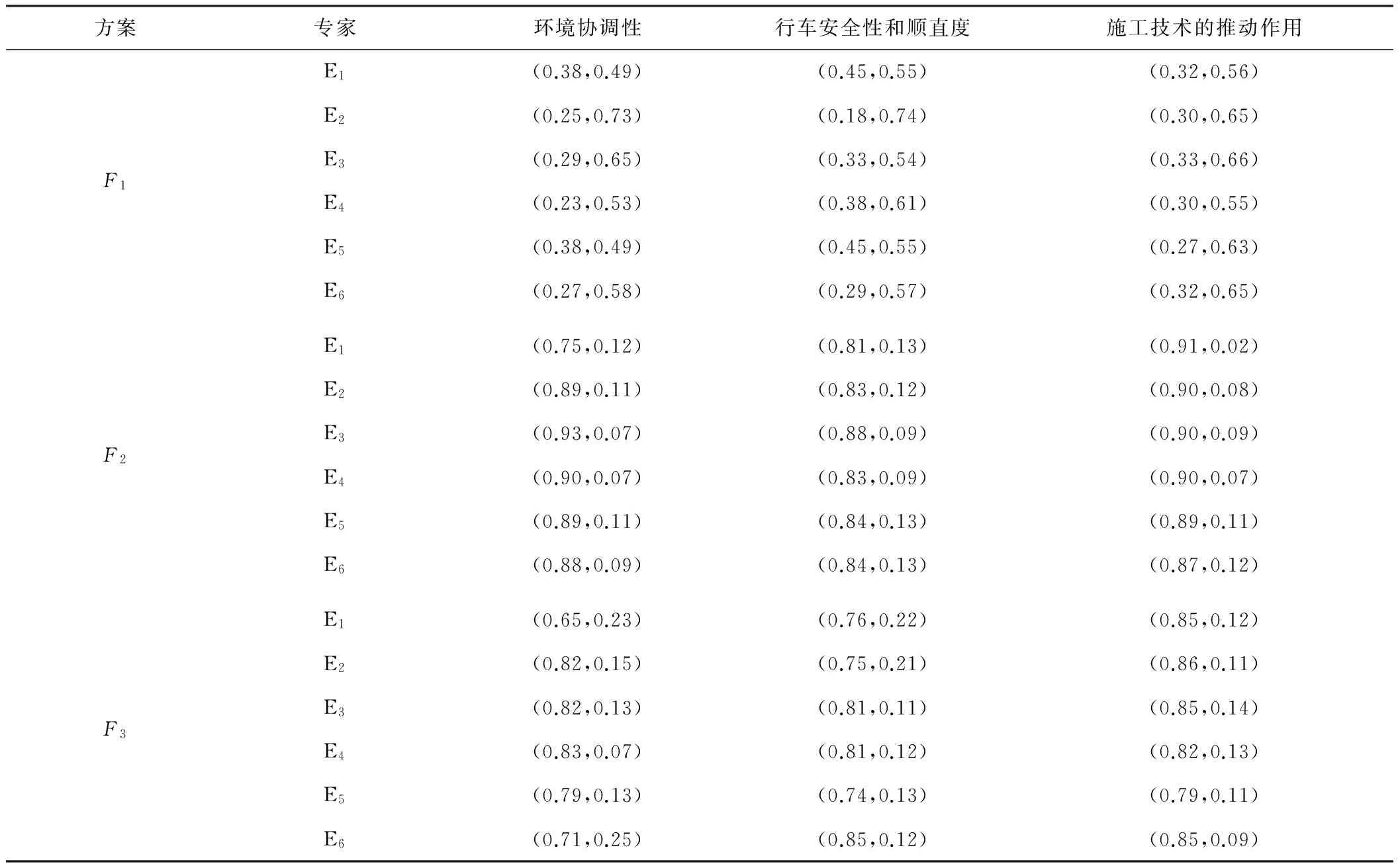
表6 社会综合效益专家指标评分表

在得到专家评分的基础上，根据上文中所述的计算原理，进行模型求解。

步骤1： 依照式(1)按照专家权向量W=(0.15,0.15,0.2,0.15,0.15,0.2)，将上述直觉模糊数矩阵进行修正，得到修正后直觉模糊数矩阵，如表7所示。

步骤2： 依照式(2)和式(3)计算αij(i=1,2,…,m;j=1,2,…,n)贴近度，得到如表8所示的αij得分矩阵。

表7 修正的直觉模糊数矩阵

表8 得分矩阵

步骤3： 计算Tij的值，结果如下。

步骤4： 依照式(4)集结所有直觉模糊数，得到各方案综合直觉模糊数如下。

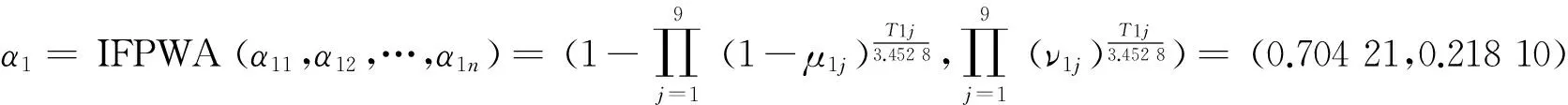
同理可得：α2=(0.602 02,0.288 70)；α3=(0.663 93,0.257 60)。

步骤5： 利用式(5)计算各方案集结结果αi(i=1,2,…,m)的贴近度如下。

C(α1)=0.725 53；C(α2)=0.641 24；C(α3)=0.688 39。

步骤6： 对步骤5中的结果进行排序，则3种方案的综合排名为F1>F3>F2，也即F1为仙岭隧道的最佳施工选择方案。

4 结论与讨论

1)考虑到仙岭隧道地质情况及各扩建方案工程特点，专家对指标进行了优先级别排序进而对各指标打分，经计算可知： 新建独立双洞的扩建形式成为仙岭隧道改扩建的最优方案。

2)由于各座隧道地形及地质差异较大，故实际优选中，各指标排序也应因地制宜，本着安全、经济、环保的原则，根据其重要程度进行相应调整。基于本文所提方法，对扩建工程中其他隧道扩建方案进行了优选，经分析论证后共有包括风霜岭隧道、大龙头隧道等在内的13座隧道推荐采用增设分离双洞的扩建方案。后祠隧道由于所处场地有限，增设双洞又易形成“小净距群效应”，施工风险较大，推荐使用组合式扩建方案。计算结果得到专家组认可，并对设计方案进行了调整。

3)本文应用海明距离-TOPSIS的直觉模糊法对厦蓉高速公路隧道改扩建施工方案进行了优选，考虑属性指标的优先级别，使得数学模型与实际中工程方案选择时关注的重点相符，分析结果更加有说服力。同时，本文在分析过程中增加专家权重，排除了偶然性和主观性，为隧道改扩建及类似工程施工方案的选取提供了一个实用的量化优选方法，大大提高了决策的科学性。

4)隧道扩建方案的选取受多种因素的影响，本文的研究仅关注主要影响因素，其他因素对评价得分的影响也应计入其中。因条件所限，本文中选取了6位专家，增加专家评判将会使优选工作更加合理。在后续类似隧道扩建方案比选，尤其是短隧道扩建方案研究中，应考虑比选方案对线形及地质环境的影响；另外，过往交通对隧道扩建施工带来的影响也应引起足够重视。

[1] 陈潇洋. 城市大跨小净距隧道原位扩建工程施工力学分析[D]. 重庆: 重庆大学, 2012. CHEN Xiaoyang. Analysis of construction mechanics of urban large span and small clear distance in-situ expansion project[D]. Chongqing: Chongqing University, 2012.

[2] 尧少敏. 既有隧道改扩建爆破开挖与监控技术研究[D]. 北京： 北京工业大学, 2015. YAO Shaomin. The study of the excavation by blasting of the reconstruction and extension tunnel and the technology of monitoring and measurement[D]. Beijing: Beijing University of Technology, 2015.

[3] 王建强, 杨云峰, 习江鹏, 等. 基于熵值法的高速公路改扩建模式选择[J]. 长安大学学报(自然科学版), 2010, 30(1): 40. WANG Jianqiang, YANG Yunfeng, XI Jiangpeng, et al. Selection of expressway reconstruction models based on entropy method[J]. Journal of Chang′an University (Natural Science Edition), 2010,30(1): 40.

[4] 郭廷泰, 韩晓虎, 安平和, 等. 基于FAHP法钢箱梁斜拉桥主梁施工方案比选[J]. 沈阳大学学报(自然科学版), 2016, 29(3): 237. GUO Tingtai, HAN Xiaohu, AN Pinghe, et al. Construction planning decision of steel box girder bridge based on FAHP method[J]. Journal of Shenyang University(Natural Science), 2016, 29(3): 237.

[5] 黄淑. 基于模糊重心理论的铁路既有线改建方案评价方法研究[D]. 成都: 西南交通大学, 2010. HUANG Shu. Study of evaluation method for reconstruction scheme of existing railway based on the fuzzy gravity center theory[D]. Chengdu: Southwest Jiaotong University, 2010.

[6] 许振浩, 李术才, 李利平, 等. 基于层次分析法的岩溶隧道突水突泥风险评估[J]. 岩土力学, 2011, 33(6): 1757. XU Zhenhao, LI Shucai, LI Liping, et al. Risk assessment of water or mud inrush of karst tunnels based on analytic hierarchy process[J]. Rock and Soil Mechanics, 2011, 33(6): 1757.

[7] 向欣, 罗煜, 程红胜, 等. 基于层次分析法和模糊综合评价的沼气工程技术筛选[J]. 农业工程学报, 2014, 30(18): 205. XIANG Xin, LUO Yu, CHENG Hongsheng, et al. Biogas engineering technology screening based on analytic hierarchy process and fuzzy comprehensive evaluation[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(18): 205.

[8] 刘伟涛, 顾鸿, 李春洪. 基于德尔菲法的专家评估方法[J].计算机工程, 2011, 37(增刊1): 189. LIU Weitao, GU Hong, LI Chunhong. Expert evaluation method based on Delphi method[J]. Computer Engineering, 2011, 37(S1): 189.

[9] 吴爱祥, 张卫锋, 郭立. 相似率价值工程法在采矿方法优选中的应用[J]. 中南工业大学学报(自然科学版), 2000, 31(4): 294. WU Aixiang, ZHANG Weifeng, GUO Li. Application of the similarity method in optimization ratio value engineering of mining method[J]. Journal of Central South University of Technology (Natural Science), 2000, 31(4): 294.

[10] 向隅. 基于三角模糊数的TOPSIS评价方法在新建铁路线路选择中的应用[J]. 石家庄铁道大学学报(自然科学版), 2011, 24(2): 56. XIANG Yu. Application of TOPSIS evaluation method based on triangle fuzzy number in new railway line selection[J]. Journal of Shijiazhuang Tiedao University(Natural Science), 2011, 24(2): 56.

[11] 贠惠娜. 基于三角模糊数-TOPSIS法的高速公路穿越高铁施工方案比选研究[D]. 西安: 西安建筑科技大学, 2013. YUN Huina. Construction scheme comparison research of highway crossing the high speed railway based on triangular fuzzy number-TOPSIS[D]. Xi′an: Xi′an University of Architecture and Technology, 2013.

[12] 武建强. 公路隧道扩建开挖方案比选及施工力学研究[D]. 重庆： 重庆大学,2009. WU Jianqiang. Study of excavation scheme comparison and construction mechanics of highway tunnel extension[D]. Chongqing: Chongqing University, 2009.

[13] 李宁, 顾强康, 张承客. 相邻洞室爆破施工对已有洞室的影响[J]. 岩石力学与工程学报, 2009, 28(1): 30. LI Ning, GU Qiangkang, ZHANG Chengke. Influence of blasting on excavation of a new tunnel adjacent to existing tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(1): 30.

[14] 夏才初, 刘志方, 单光炎, 等. 改扩建隧道衬砌振速控制值的确定和爆破参数优化的方法[J]. 绍兴文理学院学报(自然科学版),2016, 36(1): 1. XIA Caichu, LIU Zhifang, SHAN Guangyan, et al. Methods of determining control value of vibration velocity and optimization of blasting parameters during reconstruction of tunnel lining[J]. Journal of Shaoxing University (Natural Science), 2016, 36(1): 1.

[15] 李弘琳. 高速公路社会效益评价[D]. 天津: 天津商业大学, 2014. LI Honglin. EvaIuation of social benefit of highway[D]. Tianjin: Tianjin University of Commerce, 2014.

[16] ATANASSOV K. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1986, 20(1): 87.

[17] CHEN S M, TAN J M. Handling multicriteria fuzzy decision-making problems based on vague set theory[J]. Fuzzy Sets and Systems, 1994, 67(2): 163.

[18] 谭吉玉, 朱传喜, 张小芝, 等. 基于海明距离和TOPSIS的直觉模糊数排序法[J]. 统计与决策, 2015, 31(19): 94. TAN Jiyu, ZHU Chuanxi, ZHANG Xiaozhi, et al. Intuitionistic fuzzy number sorting method based on Hamming distance and TOPSIS[J]. Statistics & Decision, 2015, 31(19): 94.

[19] SZMIDT E, KACPRZYK J. Distances between intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 2000, 114(3): 305.

Intuitionistic Fuzzy Optimization of Enlargement Scheme of Highway Tunnel in Mountain Areas Based on Hamming Distance-TOPSIS Method

WU Xiaoguang1, 2, HE Pan1, 2, *, SU Xingju3, QIAN Ruolin1, 2

(1.KeyLaboratoryofBridgeandTunnelofShaanxiProvince,Chang′anUniversity,Xi′an710064,Shaanxi,China;2.HighwaySchoolofChang′anUniversity,Xi′an710064,Shaanxi,China; 3.Zhangzhou-LongyanSectionEnlargementEngineeringCo.,Ltd.ofXiamen-ChengduExpresswayinFujian,Longyan364000,Fujian,China)

The determination of rehabilitation scheme of highway tunnel in mountain areas is difficult; and there are few theoretical references. As a result, a determination method for multiple attribute problem with priority relation is put forward based on intuitionistic fuzzy based Hamming distance, TOPSIS method and expert weight vector correction. And then, the influencing factors of the rehabilitation of the highway tunnel in mountain areas are analyzed; and then the influence index system of the tunnel enlargement scheme is established. Finally, the indicators are prioritized by experts invited, and the enlargement scheme optimization is realized by mathematical model established. The successful application of the above-mentioned method to enlargement construction of tunnel on Xiamen-Chengdong Highway indicates that the method is rational and feasible, and can provide reference for tunnel rehabilitation of similar projects in the future.

Xiamen-Chengdong Highway; mountain areas; tunnel enlargement; Hamming distance; intuitionistic fuzzy sets

2017-03-13;

2017-06-20

福建省交通运输厅科技项目(201238)

邬晓光(1961—)，男，湖北英山人， 2005年毕业于西安建筑科技大学，结构工程专业，博士，教授，主要从事大跨径桥梁结构分析、桥梁维修与加固、公路施工安全控制等研究工作。E-mail: wxgwst.cn@126.com。*通信作者： 贺攀， E-mail: 1264941490@qq.com。

10.3973/j.issn.1672-741X.2017.08.002

U 45

A

1672-741X(2017)08-0926-07