一种地籍数据DWG到SHP格式转换中圆弧加密的优化算法
2017-09-03吕成亮廉光伟黄毅
吕成亮,廉光伟,黄毅
(天津市测绘院,天津 300381)
一种地籍数据DWG到SHP格式转换中圆弧加密的优化算法
吕成亮*,廉光伟,黄毅
(天津市测绘院,天津 300381)
首先总结地籍数据DWG到SHP格式转换中常用的圆弧加密算法,发现其中的不足之处,在此基础上提出一种优化的圆弧加密算法,给出该算法的实施要点,并在实际工作中加以验证。验证结果表明:优化之后的算法极大提高了圆弧加密的正确率。
地籍数据;长度不变法;面积不变法;圆弧加密优化算法
1 引 言
随着测绘地理信息技术的快速发展,测绘项目提交的成果既有基于AutoCAD制作的dwg,还包括基于ArcGIS平台的shp文件。具体工程项目中,通常先绘制dwg,然后将dwg转换成shp。由于shp不支持圆弧,如何快速准确地对CAD中的圆弧加密就成为dwg转换成shp数据的首要工作。
圆弧加密,就是用加密点连接成的多段线拟合圆弧的过程。目前常用的加密算法有两种,根据拟合限差的不同,分为长度不变法和面积不变法。两种算法在一定程度上能满足地籍数据转换的要求。但是,由于两种算法均不严谨,有时会发生加密错误。为此,本文在分析上述算法缺陷的基础上,对既有算法进行优化,并在实际工作中加以验证。
2 圆弧加密优化算法
2.1 现有两种算法
长度不变法:该算法主要用于生成线状shp时的圆弧加密,要求最终拟合圆弧的多段线长度与对应圆弧长度在有效位数上一致。其基本思想是假设对圆弧取中内插n次,形成2n段长度相等的小圆弧,每段小圆弧对应的弧长为:
(1)
每段小圆弧对应的弦长为:
(2)
弧长与对应弦长之差为:
(3)
其中:θ和r分别代表圆弧的圆心角和半径。
假设拟合圆弧的多段线长度与对应圆弧的长度差值限差为△1。如果满足条件:△1≥2n×△L,则内插停止,圆弧加密结束;否则内插继续,直至满足停止条件。
面积不变法:该算法主要用于生成面状shp时的圆弧加密,要求最终拟合圆弧的多段线与圆心形成的闭合多边形面积与对应扇形的面积在有效位数上一致。其基本思想是假设对圆弧取中内插n次,会形成2n段长度相等的小圆弧,每段小圆弧对应的扇形面积为:
(4)
每段小圆弧对应的圆心三角形面积为:
(5)
扇形与圆心三角形面积之差为:
(6)
其中:θ和r分别代表圆弧的圆心角和半径。
假设拟合圆弧的多段线与圆心形成的闭合多边形面积与对应扇形的面积差值限差为△2。如果满足条件:△2≥2n×△S,则内插停止,圆弧加密结束;否则内插继续,直至满足停止条件。
2.2 两种算法缺陷
以地籍测量为例。首先,无法保证JZX层和ZD层边线的逻辑一致性。同一圆弧进行加密时,对于JZX层,采用的是长度不变法;对于ZD层,采用的是面积不变法。由于各自采用不同的算法进行加密,ZD层的边线与JZX层无法完全重合,而考虑到界址线和宗地的逻辑关系,两者应该严格重合。
其次,面积不变法没有考虑界址线中存在多段圆弧时的情况。假设界址线中存在m段圆弧,每段圆弧加密之后,最终拟合圆弧的多段线与圆心形成的闭合多边形面积与对应扇形的面积差值为△Si(i=1,2…,m)。
在不考虑圆弧凹凸性的情况下,该宗地面积实际变化值为:
△2′=△S1+△S2+…△Sm
(7)
由2.1节可知,只能满足:
△2≥△Si
(8)
由(式7)和(式8)可推导得:
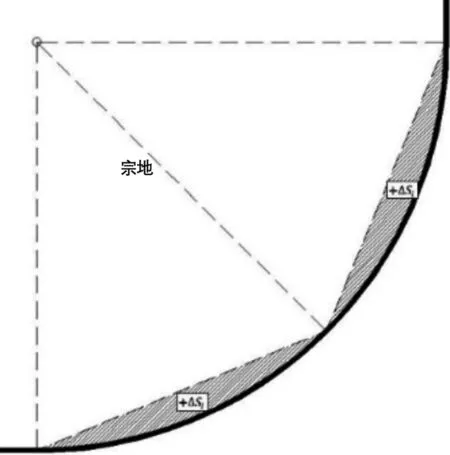
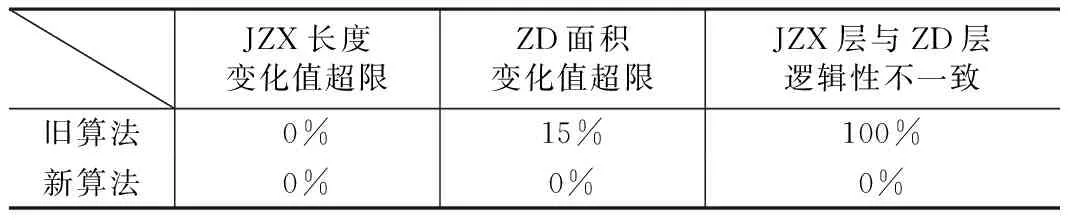
△2′ (9) 由式(9)无法判断△2′和△2的关系,且m值越大,△2′>△2的可能性越大,此时属于加密错误。 第三,没有考虑界址线中圆弧存在凹凸性的问题。如果圆心在宗地范围内,将该圆弧定义为凸圆弧,反之则定义为凹圆弧。凸圆弧加密之后,△Si会导致宗地面积减少,定义为+△Si。凹圆弧加密之后,△Si会导致宗地面积增加,定义为-△Si。 假设界址线中存在a段凹圆弧,b段凸圆弧,最终圆弧加密之后,宗地面积实际变化值为: △2″=(△S1+△S2+…△Sa)-(△Sa+1+△Sa+2+…△Sa+b) (10) 此时,△2″和△2的关系无法判断,根据a和b的取值不同,结果也会不同。 图1 凸圆弧对宗地面积的影响 图2 凹圆弧对宗地面积的影响 2.3 算法改进优化 为解决上节算法中存在的问题,提出优化之后的算法。假设某一地籍测绘项目的界址线存在a段凹圆弧,b段凸圆弧,各个圆弧对应的圆心角为θi和ri,圆弧加密之后面积差值限差为△3,长度差值限差为△4。如图3所示,给定优化算法的实施要点。 图3 优化算法流程图 新算法较原算法有两处改进: (1)改变圆弧加密完成的判定条件。新算法中,对任意一段圆弧加密,同时对长度限差和面积限差进行拟合限差判定,只有当两者都判定合格时,圆弧加密才完成。这样就能保证JZX层和ZD层在逻辑上严格统一。 (2)充分考虑存在多段圆弧和圆弧凹凸性对于加密结果的影响,使得圆弧加密结果更为精准可靠。 按照上节中所述思路,采用C#在CAD内进行二次开发编写圆弧加密工具。选取某街道在第二次土地调查中的地籍调查成果图,同时采用新旧两种算法,对所有DWG图中存在的圆弧进行加密。以宗地为单位,统计两种算法的错误率如下: 圆弧加密错误率统计 表1 由表1可知,新算法有效避免了JZX层与ZD层逻辑性不一致的问题,同时改进了原算法中由于存在多段圆弧以及圆弧凹凸性不同造成圆弧加密之后ZD面积变化值超限的问题,提高了圆弧加密的正确率。 本文首先总结现有地籍数据DWG到SHP格式转换中常用的圆弧加密算法,然后针对现有算法中存在的缺陷进行分析,进而提出一种优化的圆弧加密算法。在实际工程项目中,同时采用新旧两种算法进行加密,对比发现优化之后的算法有效地避免了原有算法中存在的各种问题,提高了圆弧加密的正确率。 [1] 陈能,施蓓琦. AutoCAD地形图数据转换为GIS空间数据的技术研究与应用[J]. 测绘通报,2005(8):11~14. [2] 张叶,孙毅中,陈年松. CAD城市基础数据到GIS转换的有关问题探讨[J]. 测绘与空间地理信息,2007(11):94~97. [3] 肖锋,吕宝奇,林蒙恩. DWG到SHP格式转换技术的研究与实现[J]. 测绘与空间地理信息,2013(9):87~89. [4] 齐立波. C#入门经典(第6版)[M]. 北京:清华大学出版社,2012. [5] 安卫. 基于VBA的两证合一SHP数据制作自动化的实现[J]. 城市勘测,2011(2):141~143. An Optimized Encryption Algorithm Used In DWG To SHP Format Conversion By Cadastral Data Lv Chengliang,Lian Guangwei,Huang Yi (Tianjin institute of Surveying and Mapping,Tianjin 300381,China) In this article,we first summarize the encryption algorithm of arc used in dwg to shp format conversion,find the deficiencies of them,and then put forward an optimized one. The results in actual work show that the new algorithm is more accurate than the old one. cadastral data;length invariant method;area invariant method;optimized encrypt- ion algorithm 1672-8262(2017)04-149-03 P209 A 2016—12—06 吕成亮(1986—),男,硕士,工程师,主要从事GPS数据处理方面的研究。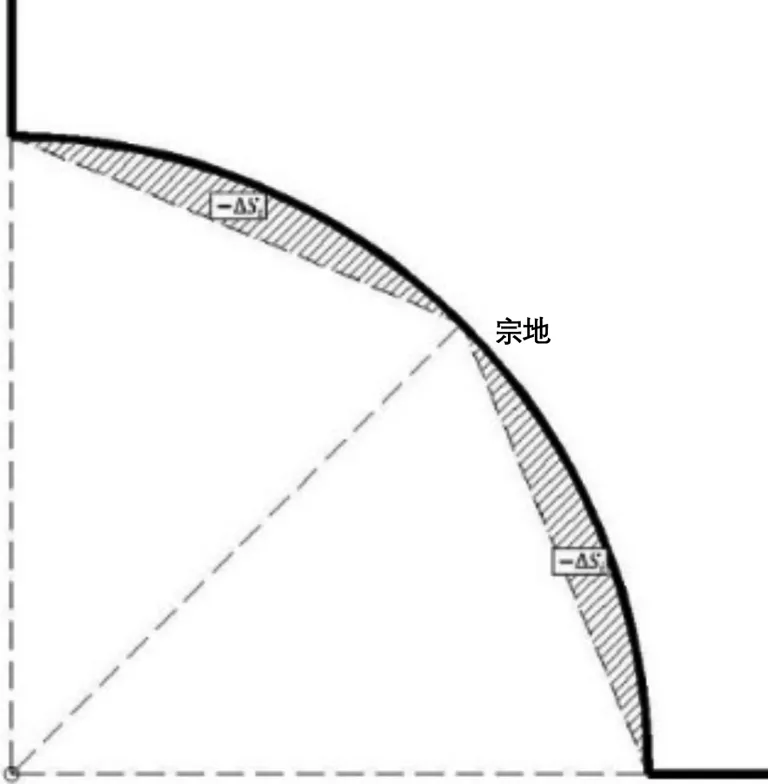

3 算法的实现与结果分析
4 结 语
