基于模糊前景理论的个人信息安全模型选择
2017-09-03李二涛
李 二 涛
(安徽经济管理学院信息工程系, 合肥 230059)
基于模糊前景理论的个人信息安全模型选择
李 二 涛
(安徽经济管理学院信息工程系, 合肥 230059)
针对个人信息安全模型的选择问题,考虑决策者的有限理性心理特征,提出一种基于前景理论的直觉模糊决策方法。通过均匀分布密度函数设计个人信息安全模型决策参考点,基于属性值与决策参考点之间的差异计算获得前景价值矩阵,构建最优化模型确定属性权重,并依据个人信息安全模型的综合前景价值进行优劣排序。
直觉模糊集; 前景理论; 均匀分布; 个人信息安全; 模型选择
针对个人信息系统进行风险评估,有助于事先发现风险并降低风险发生概率,提前为客户提供安全防范措施[1-2]。个人信息主要包含2大类:一类是社会属性信息,主要指自然人在参与社会活动中所形成的信息及他人对自然人的评价,如婚姻状况、工作单位、通讯记录、信用卡账号等信息;另一类是自然属性信息,指那些记录个人自然情况的信息,主要是一些生理方面的信息,如性别、身高、患病情况等信息[3-4]。在网络科技高速发展的外部环境下,个人信息具有内容多元化、范围限定化、主体控制力降低等特征。个人信息安全模型的选择研究成为当前重要的研究课题。
个人信息安全模型的选择,本质上属于选择决策问题。决策的目的是选择出最优的方案,使其能够尽可能地符合组织决策者的期望目标[5]。多属性决策分析方法主要分为2类。一类是基于期望效用理论的决策方法[6]。此类决策方法要求对决策问题发生的概率、事件发生的状态以及有哪些决策结果等信息能够完全掌握,且决策者在行为上追求效用最大化。另一类是考虑决策者心理有限理性特征的决策方法。此类决策方法考虑了决策者心理有限理性,更加符合实际的决策问题,逐渐成为研究的热点。考虑到决策者在实际决策过程中的有限理性,由Kahneman等人于1979年首次提出的前景理论认为决策者在决策过程中并非追求效用最大的目标,而是选择综合价值最满意的决策方案[7]。刘云志等人基于前景理论处理具有单一和组合指标期望的多指标决策问题,并将其应用于企业人才招聘过程中[8]。基于前景理论,闫书丽等人建立了三参数区间灰数型群体灰靶决策模型[9]。
本次研究中,将分析基于直觉模糊环境下的个人信息安全模型选择决策方法,运用均匀分布密度函数设计参考点,通过前景理论构建前景价值矩阵,以综合前景价值最大化建立最优化模型求解属性权重,最后使得网络服务机构选择出综合性能最高的个人信息安全模型。
1 基础理论及概念
为方便起见,记M={1,2,…,m},N={1,2,…,n},T={1,2,…,l}。
1.1 直觉模糊集定义
定义1[10]假设X={X1,X2,…,Xn}为一组个人信息安全模型,定义在X上的直觉模糊集(IFS)可表示为
A={
其中uA:X→[0,1],vA:X→[0,1]分别表示个人信息安全模型Xi∈A的隶属度和非隶属度,且满足对任意的Xi∈X,有uA(Xi)+vA(Xi)≤1。
为了便于计算,称α=
定义2[11]设α=
1.2 前景理论
现有的决策方法大部分是基于期望效用理论而提出,即假设决策者在个人信息安全模型的选择过程中是完全理性的。然而,由于现实决策的复杂性和人类思维的局限性,使得决策者在决策过程中往往表现出有限理性的行为特征。1979年,诺贝尔经济学奖获得者Kahneman等人提出前景理论,充分考虑了决策者的心理行为特征,认为决策者在选择个人信息安全模型的过程中并非追求绝对效用最大化这一目标,而是选择综合价值或性能最满意的个人信息安全模型。前景理论主要包括价值函数和决策权重,前景价值函数[7]定义如下:
(1)

2 基于均匀分布设计的个人信息安全模型参考点
在此,基于决策者给出的直觉模糊决策矩阵D=(αij)m×n,利用直觉模糊数和区间模糊数之间的关系,将直觉模糊决策矩阵转化为区间模糊决策矩阵,然后依据均匀分布密度函数求解出直觉模糊数发生的概率,进而构建个人信息安全模型参考点。
因为直觉模糊数αij=
基于得到的区间模糊决策矩阵B= (βij)m×n,同一属性Cj下所有个人信息安全模型的区间信息构成一个区间值序列{βij=[aij,bij]|i∈M},然后将该区间值序列划分为2个左右端点值序列{a1j,a2j, …,amj}和{b1j,b2j,…,bmj},于是可得这2个序列的均值:
(2)
在实际决策过程中,均匀分布是最常见的概率分布之一。因此,当属性Cj下的属性信息值x服从均匀分布时,其概率密度函数可表示为:
(3)
区间模糊决策信息βij,其属性Cj下的属性信息分布服从均匀分布,于是采用均匀分布对属性Cj下区间模糊数βij=[aij,bij]的概率进行分析,分析结果的准确率较高。假设属性Cj下属性值x的概率密度函数为fj(x),那么区间属性[aij,bij]发生的概率可表示为:
(4)
考虑到随机变量的特征,令
(5)
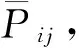

(6)
(7)
3 个人信息安全模型选择方法的构建

在个人信息安全模型的选择过程中,由于决策者在决策过程中存在有限理性特征,因此在上述分析的基础上,构建个人信息安全模型X1,X2,…,Xm的性能优劣排序方法,最终选择出综合性能最优个人信息安全模型,具体计算步骤如下:
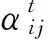
(8)
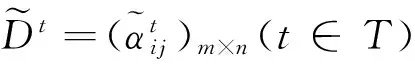
步骤二:基于状态发生概率Pt得到第θt种状态下的决策权重函数:
(9)

(10)
(11)

(12)

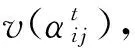
(13)
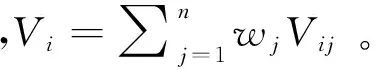
(14)
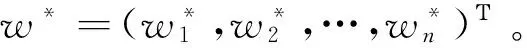

(15)
步骤七:按照综合前景价值的大小对个人信息安全模型进行优劣排序。综合前景价值越大的个人信息安全模型越能够符合决策者的期望。
4 案例分析

表1 外部环境好时的决策矩阵D1

表2 外部环境中时的决策矩阵D2

表3 外部环境差时的决策矩阵D3
接下来,运用本次构建的个人信息安全模型选择方法遴选出综合性能最优的个人信息安全模型。
首先,3种属性均为效益型属性,不必对决策矩阵进行标准化处理。根据文献[12]中的参数选择,令δ=0.89,σ=0.92,λ=2.25,ξ=0.74,依据公式(9)计算得到3种自然状态的决策权重函数为:
ω(P1)=0.434 7
ω(P2)=0.437 7
ω(P3)=0.229 9
其次,根据个人信息安全模型参考点的设计方法和公式(10) — (13),可得前景价值矩阵V=(Vij)4×3:

然后,通过模型(14)构建综合前景价值最大化的最优化模型,利用LINGO软件得到属性权重为w*=(0.201 1,0.351 8,0.447 1)Τ。
于是利用式(15)计算出每种个人安全信息模型的综合前景价值:V1=-0.024 1,V2=-0.059 5,V3=0.078 6,V4=0.319 4。
最后,因为V4>V1>V2>V3,所以判定综合性能最优的个人安全信息模型为X4。
5 结 语
在直觉模糊信息环境下,结合前景理论提出了个人信息安全模型选择方法。首先运用均匀分布密度函数设计个人信息安全模型参考点,然后通过前景理论得到不同安全模型在属性下的前景矩阵,运用最优化模型求解属性权重,进而得到每种个人信息安全模型的综合前景价值。最后将提出的选择方法运用于网络服务机构的个人信息安全模型的选择中,为保护个人信息隐私、提升组织内部的信息化能力提供科学的决策依据。
[1] 尹淋雨.大数据环境下企业信息安全水平综合评价模型研究[D].合肥:安徽财经大学,2015:10-20.
[2] 黄启发,宋彪.基于协同学的企业信息安全综合评价模型[J].现代情报,2012,32(8):113-117.
[3] 宋鹏,王有凯.网络背景下个人信息安全保护探讨[J].信息网络安全,2012(8):26- 28.
[4] 田桂兰.网络环境下个人信息安全问题与保护[J].信息法务透析,2007(1): 15-17.
[5] GUO K H,LI W L.Combination rule of D-S evidence theory based on the strategy of cross merging between evidenees[J].Expert Systems with Applications,2011,38(10): 13360-13366.
[6] MARIA A G.A note on the connection between fuzzy numbers and random intervals[J].Statistics & Probability Letters,1992,13(2): 311-319.
[7] KAHNEMAN D,TVERSKY A.Prospect theory: An analysis of decision under risk[J].Econometrica,1979,47(2): 263-292.
[8] 刘云志,樊治平.基于前景理论的具有指标期望的多指标决策方法[J].控制与决策,2015,30(1): 91-97.
[9] 闫书丽,刘思峰,吴利丰.一种基于前景理论的三参数区间灰数型群体灰靶决策方法[J].控制与决策,2015,30(1): 105-109.
[10] ATANASSOV K T.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1): 87-96.
[11] XU Z S.Intuitionistic fuzzy aggregation operators[J].IEEE Transactions on Fuzzy Systems,2007,15(6): 1179-1187.
[12] 郝晶晶,朱建军,刘思峰.基于前景理论的多阶段随机多准则决策方法[J].中国管理科学,2015,23(1): 73-81.
Research on the Selection of Personal Information Security Model Based on the Fuzzy Prospect Theory
LiErtao
(Department of Information Science, Anhui Economic Management Institute, Hefei 230059, China)
For the decision-making problems with selection of personal information security model, based on the prospect theory, an intuitionistic fuzzy decision making method is proposed, where the bounded rationality psychological characteristics of decision maker are considered. The uniform distribution density function is utilized to construct the personal information security model reference point. With the help of the difference between the attribute value and the reference point, the prospect value matrix is obtained. In addition, an optimization model is developed to derive the attribute weights, and all the personal information security models are further ordered.
intuitionistic fuzzy set; prospect theory; uniform distribution; personal information security; mode selection
2017-02-24
安徽省2013年高校省级优秀青年人才基金重点项目“多边界政务信息共享的动态监管研究” (2013SQRW115ZD);安徽省高校自然基金项目“基于UCON模型的个人隐私信息使用控制研究”(KJ2016A162)
李二涛(1972 — ) ,男,安徽巢湖人,讲师,研究方向为信息管理。
TP393
A
1673-1980(2017)04-0087-04
