复杂光照环境下电力仪表的二值化研究
2017-09-03李功燕
李 真,李功燕
(1.中国科学院大学, 北京 100049; 2.中国科学院微电子研究所, 北京 100029; 3.江苏物联网研究发展中心, 江苏 无锡 214135)
复杂光照环境下电力仪表的二值化研究
李 真1,3,李功燕2,3
(1.中国科学院大学, 北京 100049; 2.中国科学院微电子研究所, 北京 100029; 3.江苏物联网研究发展中心, 江苏 无锡 214135)
图像二值化是进行仪表识别的前提,其处理结果的好坏直接影响仪表识别的准确率。而实际拍摄的图像,受复杂光照环境的影响,会出现多种光照不均的现象,增加了二值化的难度。针对这一问题,提出一种解决方案:首先使用改进的同态滤波和自适应灰度变换法相结合的方法对图像做增强处理;然后再使用OTSU算法对图像进行二值化。实验结果表明,这种方法不仅有效去除了光照不均带来的影响,还能根据不同情况自主调节图像各部分亮度。二值化后的仪表图像连续性好,细节完整。
仪表;同态滤波;灰度变换;光照复杂;OTSU
0 引言
电力仪表是变电站中数目众多的一种检测设备,为确保变电站安全稳定地运行需要定期对仪表进行巡检。我国变电站的巡检方式正在从人工巡检向自动化巡检过渡:通过对仪表进行图像采集和自动识别系统完成仪表的自动化巡检。而仪表二值化是进行仪表自动化识别的基础,二值化的效果直接影响识别率[1-2],因此有必要对仪表的二值化方法进行研究。
变电站的仪表放置在露天环境,采集的图像容易受到光线干扰,增加图像二值化难度。为了减小光照带来的影响,有几种常见的处理方法:灰度变换法[3]、Retinex增强法[4]和同态滤波法[5-8]。这些方法虽然能够改善图片的质量[9-10],但是由于算法的自适应能力差,不足以解决复杂光照环境下的仪表二值化问题。为此本文提出一种解决方案:先利用改进的同态滤波算法和自适应灰度变换法处理图像,然后利用OTSU算法进行二值化。通过实验对比分析,本文提出的方法能够有效解决复杂光照环境下的仪表二值化问题。
1 复杂环境下仪表的二值化问题
实际拍摄中,主要存在3个问题:光线过亮、光线过暗和光线不均匀。图1中的3组仪表图片分别显示了这三种情况。

图1 复杂环境下图像二值化问题
从图中可以看出,无论是采用局部二值化还是全局二值化都无法满足系统对于在复杂光照环境下拍摄的仪表图像进行二值化的要求。因此,有必要在进行二值化处理前,对图像做增强处理,来减小光照不均和对比度低带来的影响。
2 改进的同态滤波
2.1 同态滤波原理
图像f(x,y)可以用两个分量来表示: (1)入射到被观察场景的光源照射总量(入射分量i(x,y));(2)场景中物体所反射的光照总量(反射分量r(x,y)),即:
f(x,y)=i(x,y)r(x,y)
(1)
这种表示方式称为图像的照射-反射模型。其中,入射分量的性质取决于照射源,与频域空间中的低频部分对应;而反射分量的性质取决于成像物体的特性,与频域空间中的高频部分对应。因此,在频域中降低低频分量可以有效降低光照不均对图像造成的影响。同态滤波就是应用这一模型开发的一种频率域图像处理方法。它将照射分量i(x,y)和反射分量r(x,y)分开,利用压缩低频、提高高频的方法,达到减弱入射分量同时增强反射分量的目的。因此同态滤波常用于对光照不均匀的图像的预处理[4]。同态滤波处理的全过程如图2所示。

图2 同态滤波处理流程图
f(x,y)为原始图像,后面的处理过程依次为:对数变换、傅里叶变换、滤波处理、傅里叶逆变换和指数运算,得到处理后的输出图像g(x,y)。其中同态滤波函数H(u,v)的选择决定了最后的处理效果。
2.2 滤波器选取及滤波效果
传统同态滤波的滤波函数是根据高通滤波函数得到的,最常使用的是Butterworth型的同态滤波器:
(2)
其中,Rh代表高频增益,Rl代表低频增益,D0为截止频率,c代表滤波器函数斜面的锐化强度。该滤波器的函数图像如图3所示。

图3 同态滤波函数示意图
在传统的同态滤波函数中,参数0

图4 原始图、同态滤波处理及二值化图
由图4(b)可知,经过传统同态滤波处理后,图像光照更加均匀,有较好的视觉效果。但是图4(c)的二值化效果不理想,图像的光照不均匀问题仍然存在,无法满足系统对电力仪表进行二值化的需求。
为了更好地去除入射光的影响,本文提出改进的同态滤波算法,将滤波函数改为:
(3)
本文将参数c设为1,R取1.5,利用改进的同态滤波对图像进行处理,其效果如图5所示。

图5 改进的同态滤波处理图像
与传统的同态滤波相比,利用改进后的滤波算法对图像进行处理后,整幅图像的亮度不再有明显的变化,达到了去除入射光影响的目的。但是由于处理后的图像对比度较低,需要做进一步处理。
3 自适应的对比度增强
为了解决滤波处理后出现的问题,本文提出自适应的对比度增强算法,其处理流程如图6所示。

图6 自适应对比度增强流程图
3.1 自适应直方图均衡化
传统的直方图均衡化是采用灰度统计特征,将原始图像中的灰度直方图从较为集中的某个灰度区间转变为均匀分布于整个灰度区域的方法。图7展示了利用传统直方图均衡化处理图像的效果,可以看出均衡化后的图像其灰度不再集中于高灰度区域,对比度明显,但是却存在着严重的块状效应。

图7 传统直方图均衡化
为了避免块状效应,本文提出一种自适应的直方图均衡化方法。该方法结合图像自身的特点在一定范围内进行均衡化,具体实现步骤如下:
(1)计算图像的灰度均值T, 且规定处理的像素点灰度转换到[0,T]区域。
(2)遍历图像中的每个点,并将该点的灰度值与T进行比较,判断该点是否为待处理点。
(3)若其灰度值大于T,则不做处理;小于等于T的点标记为待处理点。
(4)将所有的待处理点进行直方图均衡化,将这部分像素点的灰度直方图转变为[0,T]区间上均匀分布的直方图。
使用这种方法对图像均衡化的结果如图8所示。从图中可以看出这种方法提高了图像对比度,同时有效避免了块状效应。

图8 自适应的直方图均衡化
3.2 自适应分段线性变换
自适应的直方图均衡化能够有效处理平均灰度较高的图像,对于平均灰度很低的图像,将采用自适应的分段线性变换进行处理。本文提出的变换函数如式(4)所示,其中T为图像的平均灰度,r为待增强图像某一像素点的灰度值,s为增强后的灰度值。
(4)
图9为这一变换函数的示意图。使用这一变换函数进行处理时,大于T的高灰度部分会以1/3的斜率进行压缩,而低于T的低灰度部分会根据T值的不同产生动态斜率进行拉伸。根据处理图像的特点,动态地确定转折点T的位置,可以更好地适用于各种图像。
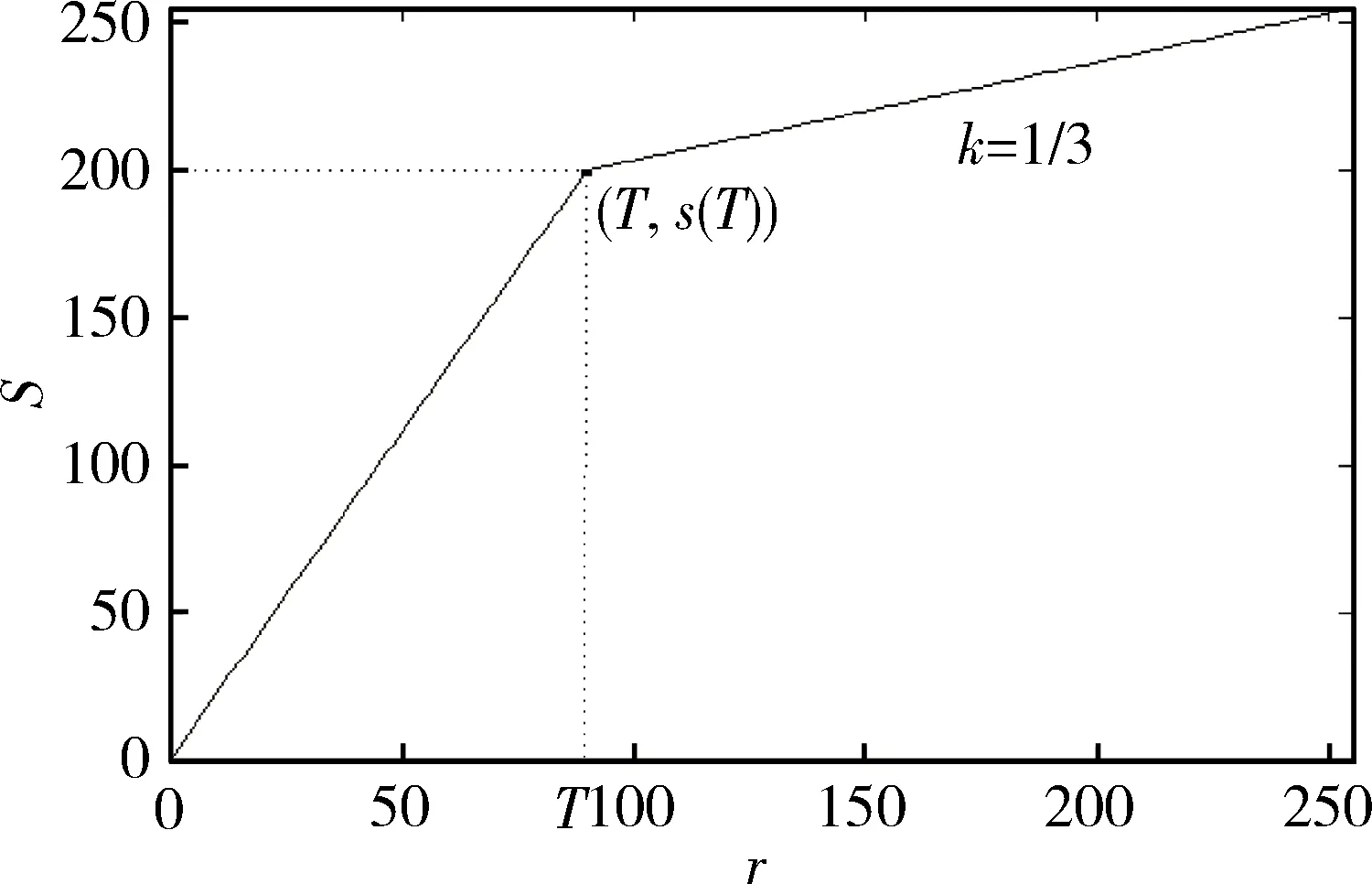
图9 自适应分段线性变换函数示意图
图10展示了使用自适应分段线性变换处理图像的效果。可以看出,处理后的图像对比度得到明显提高,有利于图像的二值化处理。

图10 自适应分段线性变换
4 算法流程
为了解决复杂光照环境下的仪表二值化问题,提出使用改进的同态滤波和自适应灰度变换进行预处理,再利用OTSU算法进行二值化的处理算法,算法处理流程为:
(1) 图像灰度化,然后使用改进后的Butterworth同态滤波器进行滤波处理。
(2) 计算图像的平均灰度值T,根据T和Th的关系将图像分为两类。
(3) 对两类图像分别进行自适应的直方图均衡化处理和自适应分段线性变换处理。
(4) 利用OTSU算法进行图像二值化。
其中,Th为多次实验得出的阈值,针对要处理的数字仪表,这里的阈值选为120。
5 实验结果与分析
本文以变电站内的一种数字式电压表为测试对象,所有图像均在变电站内利用可见光相机采集得到,且拍摄时间由上午9点到下午5点不等。图11是利用不同算法对不同图像进行二值化的效果。其中,(a)为相机采集原图;(b)为使用局部阈值法进行二值化得到的图像,这种方法可有效克服光照不均的影响,但是二值图像存在断裂且在处理低对比度图像时效果很差;(c)是使用同态滤波和局部阈值法进行二值化得到的图像,得到的二值图像细节更完整,但是会引入大量的干扰噪声;(d)是使用同态滤波、灰度变换和局部阈值法进行二值化得到的图像,图像中仍然存在大量噪声,与图(c)相比,并没有明显的改善;(e)是使用OTSU算法得到的二值图,这种方法受光照影响很大,虽能保证数字的连续性但是处理复杂光照下的图像效果很差;(f)是同态滤波和OTSU方法,二值图像中数字连续性好且细节完整,但是图像中有较多的噪声块;(g)是使用本文方法处理后的二值图,图像中数字清晰完整,噪声干扰很少,处理效果理想。

图11 多种方法二值化对比图
本文对二值化后的数字采用卷积神经网络法进行识别并以数字的识别率衡量二值化效果。表1显示了各种处理算法的识别率情况,结果显示:对于视觉效果较好的图像,几种方法的识别率都较高;对于视觉效果较差的图像,本文方法显示了极大的优势。考虑到室外环境的复杂多变,使用本文方法是最适合的。

表1 不同处理方法的性能对比
6 结论
本文提出一种适用于复杂光照环境下的仪表二值化方法。该方法首先使用改进的同态滤波处理图像,最大可能地减少入射光的影响;然后根据图像的具体情况动态地变换灰度,这样可以动态地提高图像的对比度;最后使用全局OTSU法对图像进行二值化。实验结果表明,该方法能够有效处理在复杂光照环境下采集的仪表图像,得到的二值化图像数字连续且细节完整,有利于后续的识别处理。
[1] 刘文亮. 七段式数显仪表中数字识别的研究与实现[D]. 大连:大连理工大学, 2013.
[2] 申森, 李艾华, 姚良, 等. 基于小波包和 Niblack 法的枪号图像二值化算法[J]. 光子学报, 2013, 42(3): 354-358.
[3] 余成波,孔庆达,钱泽文,等.基于双向多项式拟合的动态阈值分割算法[J].电子技术应用,2016,42(3): 110-112.
[4] 侯晓然,秦丽娟,王永.改进Retinex算法对特殊环境下的车牌图像增强研究[J].微型机与应用,2015, 34(19): 50-53.
[5] AGARWAL T K, TIWARI M, LAMBA S S. Modified histogram based contrast enhancement using homomorphic filtering for medical images[C].Advance Computing Conference (IACC), 2014 IEEE International. IEEE, 2014: 964-968.
[6] 梁琳,何卫平,雷蕾,等.光照不均图像增强方法综述 [J].计算机应用研究,2010,27(5):1625-1628.
[7] HILL P R, BHASKAR H, AL-MUALLA M E, et al. Improved illumination invariant homomorphic filtering using the dual tree complex wavelet transform[C].2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, 2016: 1214-1218.
[8] ADELMANN H G. Butterworth equations for homomorphic filtering of images[J]. Computers in Biology and Medicine, 1998, 28(2): 169-181.
[9] 郭佳, 刘晓玉, 吴冰, 等. 一种光照不均匀图像的二值化方法[J]. 计算机应用与软件, 2014, 31(3): 183-187.
[10] YU Z, BAJAJ C. A fast and adaptive method for image contrast enhancement[C]. International Conference on Image Processing, IEEE, 2004: 1001-1004.
Study on meter binarization method under complicated illumination
Li Zhen1,3, Li Gongyan2,3
(1. University of Chinese Academy of Sciences, Beijing 100049, China; 2. Institute of Microelectronics of Chinese Academy of Sciences, Beijing 100029, China; 3. Jiangsu R&D Center for Internet of Things, Wuxi 214135, China)
The image binaryzation is the precondition of meter recognition and its performance will influence the accuracy rate of the recognition directly. However, in practice, the uneven illumination situation will arise because of complex light conditions, thus increases the difficulty of image binarization. To solve this problem, this paper proposes a new approach. Firstly, one method which combines improved homomorphic filtering with dramatic adaptive grayscale transform is used to enhance the image quality. Then, in order to get stroke continuous digital images, this method use OTSU algorithm to binary digital images. Experimental results show that this method not only eliminates the effect of the uneven illumination but also adjusts brightness of different areas in images by different situation independently. After processing by proposed method, the results of image processing retains more details and continuity.
meter; homomorphic filtering; gray transformation; complicated illumination; OTSU
TP391.4
A
10.19358/j.issn.1674- 7720.2017.15.013
李真,李功燕.复杂光照环境下电力仪表的二值化研究[J].微型机与应用,2017,36(15):45-48.
2017-03-17)
李真(1990-),女,硕士,主要研究方向:数字图像处理、模式识别。
李功燕(1979-),男,博士,研究员,主要研究方向:图像处理&多核DSP系统,机器人与智能制造。
