《中国古代音乐史的律学暨律种学》之教学设计

胡企平

《中国古代音乐史的律学暨律种学》之教学设计

胡企平

在中国高校音乐学专业的 《中国古代音乐史》教学中，讲授 《中国古代音乐史的律学暨律种学》这一教学单元时，针对大学生的认知特点与规律，紧密围绕音乐声学的教学特点与方法，对我国历代乐律学家在 “以耳齐其声”的音乐文化大背景下，他们如何运用数学手段对琴律律种学 “弦鸣振动”、管律律种学 “气鸣振动”和钟律律种学 “体鸣振动”所进行的律学探索与研究成果进行了梳理，并与我国改革开放以来的古代音乐考古学研究成果紧相结合，精心设计成为6课时仨律种学的溯源探流教案。

律学；律种学；音乐声学；中国古代音乐史

引 言

在笔者主讲的 《中国古代音乐史》课程中，《中国古代音乐史的律学暨律种学》（以下简称《律学暨律种学》）的教学计划是6课时，内容包括琴律、管律和钟律。它们的名称既和古代乐器所制作采用的原材料及其发声循律的器具密切相关，又分别代表着上述三类各自不同的发音体及其振动方式，由于教学内容牵涉到音乐声学的声律方法与声律公式，难免使得音乐教育和音乐表演专业的学生在听课时感到枯燥、乏味。

教学参考资料主要是相关的文献资料。随着二十世纪下半叶中国音乐考古学的发展，尤其是1978年湖北省随县曾侯乙墓64枚编钟和琴、瑟等共计125件古乐器的出土，以及1986年在河南省舞阳县贾湖村新石器时代早期遗址中一批用鹤胫骨制成的 “骨笛”的出土，加上考古学家和音乐专家对这些古代乐器的相关考证、测试数据和模拟演奏视频等，为丰富这6课时的教学内容提供了大量的声学原理数据和生动的具象演奏，也为 《律学暨律种学》教学过程的数据化和可感性增色不少。

当然，教师还需对整个教学过程进行缜密的教案设计，再加上教学法的充分运用，这才使得 《律学暨律种学》课的教学目标实现成为可能。

为此，笔者拟定本单元的教学目的为：

（一）通过本课教学，使学生了解琴律、管律和钟律等仨律种学各自不同的发音体及其声律振动方式，以及琴律 （弦鸣振动）、管律 （气鸣振动）和钟律 （体鸣振动）的振动图像及其音乐声学公式，以提高他们综合地理解和分析音乐声学基础知识和相关的计算能力。

（二）笔者设计的三个教案分别是：

1.琴律律种学教学与鉴赏 （2课时）；

2.管律律种学教学与鉴赏 （2课时）；

3.钟律律种学教学与鉴赏 （2课时）。

一、琴律律种学之教学与鉴赏

律的计算方法种类很多，最基本的有弦长比和频率比两种计算方法，其它的种种计算方法，都是在这两种计算方法的基础上派生出来的。其中，弦长比是以音阶中各振动弦长为核算依据来求证各音与宫音，以及各音自身之间的音高关系，弦长比计算法的优点是可以通过直接测量琴弦振动部分的长度，在不必测量其振动频率的情况下，即可求出音阶各音之间的音高比例关系。因此，我国古代弦律律种学的计算，基本上都是沿用了弦长比的计算方法。

（一）古代弦长比的计算方法

1. 《管子》的“三分损益法”［1］52⁃53

关于生律法的记载，最早见于春秋时代管仲（卒于前645）所传的 《管子》一书，此书的 《地员篇》中说明了如何用 “三分损益法”来生律。

所谓 “三分损益法”，就是先将弦振动发音体的长度三等分，“三分损一”，即舍去其三分之一，取其三分之二 （1×2/3＝2/3）， 以生其上方的纯五度音；“三分益一”，即增其三分之一，成其三分之四 （1×4/3＝4/3）， 以生其下方的纯四度音。《管子》 设 “宫”（do） 的律数为34＝81，先 “三分益一”，再 “三分损一”，生律四次，得五律：

34＝81 （宫， Do）

81 （三分益一） ×4/3＝108 （徵， sol）

108 （三分损一） ×2/3＝72 （商， re）

72 （三分益一） ×4/3＝96 （羽， la）

96 （三分损一） ×2/3＝64 （角， mi）

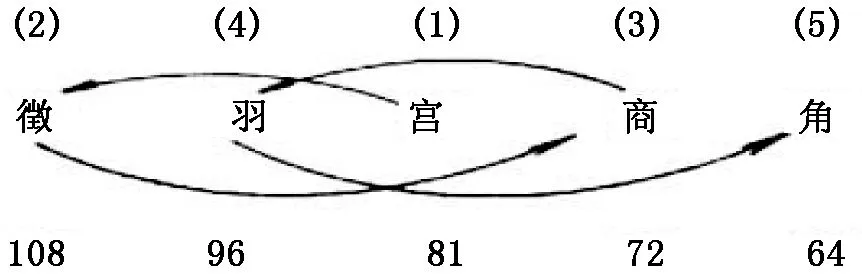
2.《吕氏春秋》的 “三分损益法”

由于用 “三分损益法”所生的五律已构成五声音阶，所以 《管子》的律学计算只止于五律。但仅此五律的律数不符合十二律的需要，故 《吕氏春秋》（发表于公元前239年）在 《管子》生五律的基础上，继续用 “三分损益法”再生七律，合为十二律。

表1

3.《淮南鸿烈》的 “律数”生成法

《吕氏春秋》虽然记载了如何用 “三分损益法”生十二律，但没有象 《管子》那样标明每一律的律数。因此，汉代刘安 （前179—前122）主持编写的 《淮南鸿烈》曾尝试用 《管子》所定的81为黄钟 （C）的律数 （其生律法改用先 “三分损一”生上方的纯五度音），但发现在第五次生“应钟”（b）起就得不到整数的律数，所以又另立了311＝177，147为黄钟 （C）的律数；这样，其所得的三分损益十二律数就全成为整数。

此外，司马迁 （前145—前89？） 的 《史记·律书》在计算三分损益十二律时，采用了分数的形式。他设黄钟 （C）的律数为1，则其他十一律的律数全是分数。

4.“三分损益律”与 “毕达哥拉斯律”的比较

用 “三分损益法”产生的律制在中国就称“三分损益律”。这种律制的基本原理与古希腊同样运用弦长比计算方法的 “毕达哥拉斯律”（Py⁃thagorean intonation）是相通的。所以，有些学者也称中国的 “三分损益律”为 “毕达哥拉斯律”。但仔细比较，其实不然，两者还是有区别的。

由于 “三分损益律”采用 “三分损一”和“三分益一”的生律方法，所以只造成了向上方纯五度、向下方纯四度的生律结果；而 “毕达哥拉斯律”是以向上方纯五度或向下方纯五度生律，因此，其 “五度圈”中的十二律除了六律与 “三分损益律”相同之外，其他六律是不相同的。请看下面表2的对照：

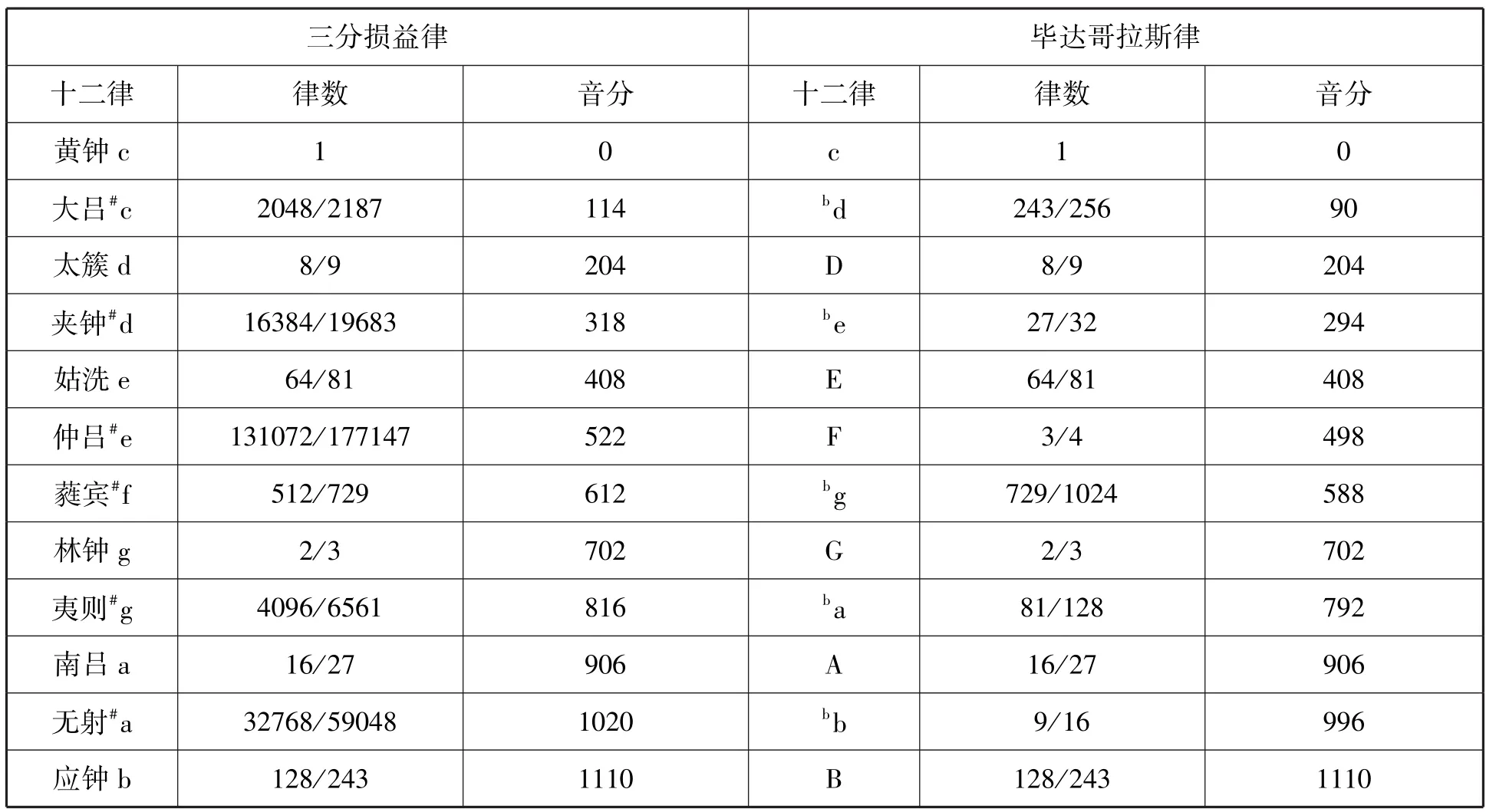
表2

通过上表2中的比较可知，在 “三分损益律”中的变化音都带升记号，“仲吕”律也只能是＃e。“毕达哥拉斯律”因可以由c生下方纯五度的F，转位后成f，其他变化音由此都带降号（b），故在两者同样的七声音阶中，其第四度音就有＃e和f的区别。这就表明了 “三分损益律”和 “毕达哥拉斯律”之间是不能划上等号的。

（二）七弦琴、十三徽位与徽法律

1.无柱的乐器在周代泛称 “琴”。关于其弦数，当时曾有：“琴本五弦，文王、武王加二弦”的传说；但从出土的情况来看，弦数不一。现今所能见到的最早的琴是曾侯乙墓出土的一张五弦琴与一张十弦琴。而图1则为湖北荆门郭店出土的一张七弦琴，此琴为现今考古发现最早的七弦琴实物，其形制与曾侯乙墓出土的十弦琴较为接近。

图1

图2为曾侯乙墓出土的一张十弦琴，木质，由琴身与一活动底板构成。活动底板垫于琴身下，底板内存有4个琴轸。全器通体髹黑漆，无琴徽。两者应有同源关系。

图2

2.两汉三国时期 （前206—280），后世古琴七弦十三徽的形制在当时正逐渐确定下来。尽管至今尚未发现具有琴徽的汉代古琴实物，但从两汉三国的文献中还是隐约可见琴徽的影子，如：西汉枚乘《七发》中提及可能是琴徽的 “九寡之珥以为旳”；汉刘安 《淮南鸿烈·修务训》中描写盲人弹琴的“参弹复徽”；魏末稽康 （223—262） 《琴赋》中所提及徽的材料及其作用的 “徽以中山之玉”“弦长故徽鸣”等语。

到了两晋南北朝时期 （265—581），“琴”在这一时期受到文人音乐家的格外推崇，古琴独奏艺术迅速发展，琴乐也因此而有了很大的发展。突出的一例即是目前仅见的一首以文字记谱的琴曲——《碣石调·幽兰》。

《碣石调·幽兰》的琴谱为唐人手抄本，现藏于日本东京国立博物馆。据谱前小序说：“丘明，会稽人也，梁末隐于九嶷山。妙绝楚调，于 《幽兰》一曲尤特精绝。”可见此曲为南朝梁丘明（494—590）所传。《古琴曲集》中存有管平湖据《古逸丛书》本的译谱。全曲共分四段，节奏变化较多，十三弦上的泛音都已用到，还保留了一些古老的演奏指法。从 《碣石调·幽兰》的琴谱不难看出，当时的古琴不仅已具备了七弦十三徽的形制，且记谱法也已是相当精细，这说明我国古琴艺术在南北朝时期就已经发展到了相当高的程度。

此曲采用了徽法律的定弦法，以 “正调”定弦，七条弦散音完全合乎徽法律的五声音阶，加上琴上具固定比例关系的泛音徽位和按音，以及用长度和徽名间记录的徽间音也都合乎徽法律。

3.徽法律和西方纯律的相同点

（1）从律制的形成来看，双方都是基于泛音列原理构成的。

（2）从音阶来看，徽法律五声音阶与西方的纯律大调五声音阶是相同的。徽法律五声加清角和变宫的七声音阶与西方的纯律大调七声音阶也是相同的。现列表3比较如下：

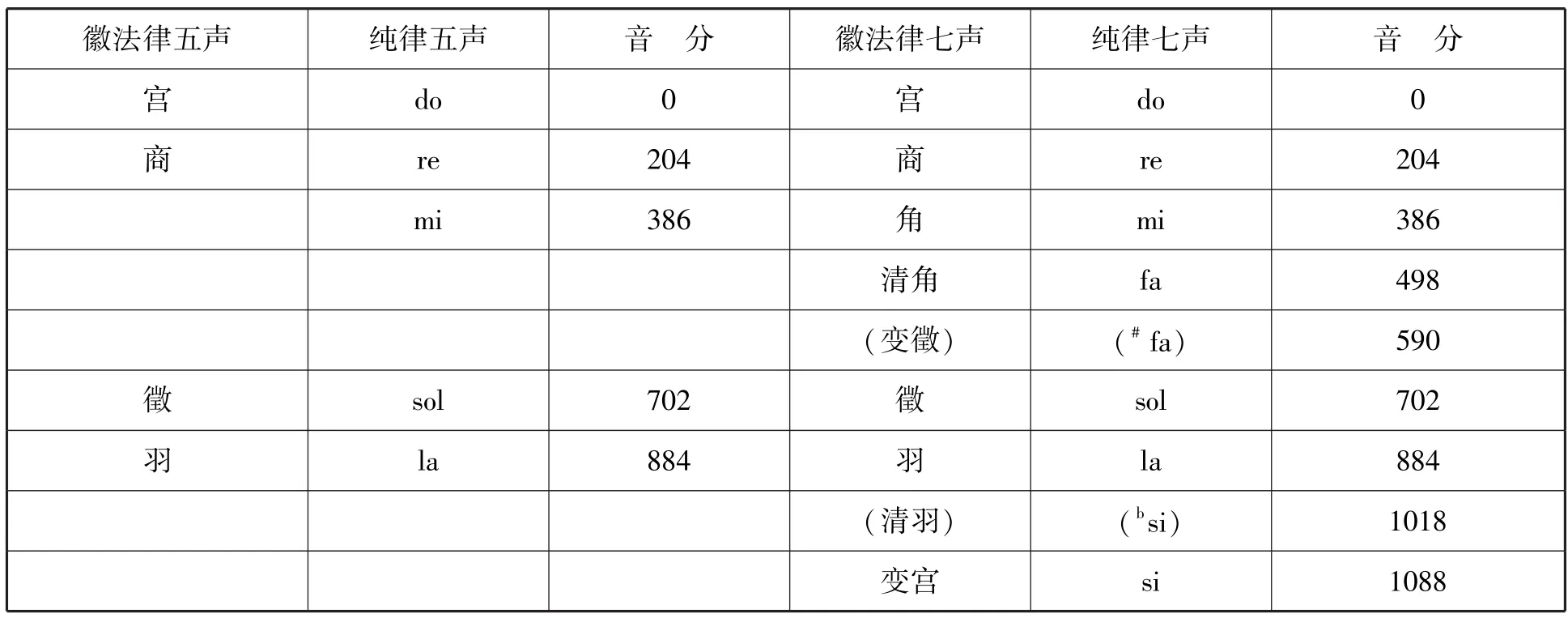
表3 徽法律、纯律音阶比较表［2］60

（3）从音程结构来看，由于双方所用的音阶相同，故双方具有的特殊音程也是相同的。

①全音音程有大、小之分：大全音204音分（如宫和商之间、清角和徵之间、羽和变宫之间），小全音182音分 （如商和角之间、徵和羽之间）；

②四度音程有纯、宽之分：纯四度498音分（如下徵和宫之间、宫和清角之间、商和徵之间、角和羽之间），宽四度520音分 （如下羽和商之间）；

③五度音程有纯、窄之分：纯五度702音分（如下徵和商之间、下羽和角之间、宫和徵之间、角和变宫之间、清角和少宫之间），窄五度680音分 （如商和羽之间）。

上述音程之大小、纯宽、纯窄的区别，都各相差一个 “普通音差”（22音分）。

4.徽法律和纯律的相异点

（1）从生律法角度来看，纯律应用基于泛音列中的八度、五度和大三度音程生律；徽法律不仅可以应用基于泛音列产生的八度 （七徽）、五度（九徽）、大三度 （三、六、八、十一徽）音程生律，而且还可以应用琴上十三徽中的大六度 （八徽）、纯四度 （十徽）、大三度 （十一徽）、小三度（十二徽）按音直接生律，更为简便。

（2）从旋宫转调来看，由于此种音阶相邻音有大小全音之别，故纯律在键盘乐器上使用时，凡遇到转调就很难保持纯律音准的一致，故不得不采用加键的办法，但徽法律仅在七弦琴上使用，既可用明徽 （即肉眼看得见的徽位），又可用暗徽 （即肉眼看不见的，但在实际存在着的 “节点”），演奏旋宫转调的乐曲并无困难。

（3）从律制应用时间来看，徽法律音阶至迟已在公元6世纪南北朝梁代琴家丘明所传的琴曲《碣石调·幽兰》中得到应用；而纯律大调音阶到了公元16世纪才由意大利著名音乐理论家查里诺（Giosephe Zarlino，1517—1590） 调出， 两者先后相差了约十个世纪。

（三）朱载堉与新法密率 （即十二平均律）［2］295⁃301

公元16世纪的明代，朱元璋皇帝的第九世孙朱载堉 （1536—1611）终于在总结前人律学研究成果的基础上，完成了十二平均律的数理计算，他称这种律制为 “新法密率”。

朱载堉发现了三分损益十二律之所以不能还生“黄钟”本律和实现象天体运行那样 “周而复始”的转调，是因为 “三分损益法”用 “三分损一”产生的五度音程太宽，而用 “三分益一”产生的四度音程太窄。于是在其所著的 《律历融通》（1581）中首先公布了改变 “三分损益法”的新方法：把 “三分损一”（1×2/3＝2/3） 的分母缩小，即把 2/3变成 500000000/750000000， 然后调整成500000000/749153538。这样，原来的 “三分益一”就成了1000000000/749153538。朱载堉用这两个数取代了 “三分损一”和 “三分益一”，并仍沿用“三分损益法”的生律顺序，取得了 “仲吕”还生“黄钟”本律的结果。其所生的十二律，即今之十二平均律。在同书中朱载堉还公布了另一种反生法，即先由 “黄钟”生上方的四度音 “仲吕”，再由 “仲吕”生下方五度音 “无射”，如此往返生律，最后由 “林钟”还生 “黄钟”本律。其方法：生上方四度音时乘500、 000、 000/667、 419、 927；生下方五度音时乘 1、 000、 000、 000/667、 419、927。这样生律的结果，其十二律也一样是十二平均律。

朱载堉在 《律吕精义》（1596年作序）中又公布了另两种 “新法密率”的生律方法：

（1）由 “黄钟” （c）连续小二度生律至 “黄钟”的高八度音 “黄钟半律”（c1），每次乘500、000、 000/529、 731、 547；

（2）由 “黄钟半律”（c1）连续小二度生律至“黄钟半律”的低八度音 “黄钟”（c），每次乘1、000、 000、 000/943、 874、 312。

朱载堉在同书中解释了上述四种生律方法的构成原理。他先设 “黄钟”（c）的律数为2（尺），开平方得 “蕤宾”（＃f）：＝1.414213562373095048801689（尺）；然后再将 “蕤宾”之数开平方，就得 “南吕”（a）：＝1.1892071150027210667175 （尺）；再用此 “南吕”的律数开立方，就得 “应钟”（b）的律数：＝1.059463094359295264561825（尺）。朱载堉得到了 “应钟”的律数，已经求出“新法密率”十二律中一律的比值，因此，他指出欲求得高一律的律数，只要将低律的律数除以这个律的比值数即可得。如前 “大吕”（＃c）：

“黄钟”（c） 2÷1.059463094359295264561825＝ “大吕” （＃c） 1.887748625363386993283826

朱载堉在 《律吕精义》中详细地开列了用这种方法计算出来的十二律律数。为表示其精确起见，每一律的律数都长达二十五位数字 （不足者小数点后补以0，如 “南吕”后有两个0）。有了这些律数，当然可以派生出前述各种各样的十二平均律生律法来了。

朱载堉在完成十二平均律数学计算的同时，在《律学新说》（1584年作序）中又设计了一台以实验他 “新法密率”的十二弦 “准”，他称之为 “均准”。“准”上的十二弦代表十二律，在 “准”的面板上，中间设有按十二平均律计算出来的标记，并以此和 “三分损益律”的律度作比较。按照准面上的十二平均律标记，在 “准”上可以调出十二平均律的定弦来。

这里，对朱载堉发明十二平均律的年代尚需作补充说明：朱载堉为 《律历融通》一书作序的日期是公元1581年2月6日。这表明在这个日期之前朱载堉已经完成了十二平均律的数学计算。但他在此书中未详列计算公式，仅在书中写道：“其详则见诸 《律吕精义》云”。由此可见，《律吕精义》完成于 《律历融通》之前。因为在公元1595年旧历8月朝廷向朱载堉徵诏律书，故朱载堉就将已经完成的 《律吕精义》作了修订，才于公元1596年1月29日作序。因此，朱载堉发明十二平均律的时间，应该算为公元1581年2月6日之前。

（四）鉴赏曲目

1.琴曲 《碣石调·幽兰》，管平湖据 《古逢丛琴谱》定谱，土逢记谱，管平湖演奏；

2.琴箫合奏 《梅花三弄》，演奏：刘丽 （古琴），陈涛 （箫）；

3.琴曲 《流水》（视频），李祥庭演奏，广东电视台 “一曲难忘”摄制组制作。

二、管律律种学教学与鉴赏

（一）管律律种之气鸣乐器的发音与空气柱振动状态分类［3］20⁃25

就气鸣乐器发音的空气柱振动状态而言，可以分为以下三类：

1.吹口锐边振动 （如长笛、竖笛、竹笛、箫和埙等）；

2.簧振动 （如单簧管、双簧管、唢呐、笙、口琴、手风琴和簧风琴等）；

3.唇振动 （如小号、长号等）。

朱载堉认为，律管之吹口 “状如箫口，形似洞门，俗名洞箫以此”。因此，律管属气鸣乐器中的吹口锐边振动类，其振动如箫。

（二）吹口锐边振动的特性分析

就吹口锐边振动的特性而言，在吹口锐边振动的管乐器中，以空气柱原理构成其振动的特性。所谓空气柱振动是当管中空气柱被激发后，会产生纵向 （与管长方向一致）的振动与横向 （与管长垂直）的振动。因为空气是流体弹性物质，所以空气柱振动同弦的振动相反，以全长纵振动为主，它决定了振动的基频和一系列泛音的频率。与此同时，横振动会分为二节、三节、四节、五节等，产生高次泛音 （即所谓的柱面波）。正是由于空气柱振动中不同份量的纵振动和横振动的迭加构成复合音，从而形成了吹管乐器的不同音色特点。

空气柱振动的另一特点是，管子越长、越宽（直径越大），则频率越低，反之亦然。此外，气柱振动如果运用 “超吹”（overbrowing）（例如，在律管上运用缩紧嘴唇、使劲送入气息的吹奏法），可以使同一长度的气柱产生高八度、高十二度乃至高两个八度等较高的音。

（三）吹口锐边振动的结构分类与分析

就吹口锐边振动的振动结构而言，又可分为开管和闭管两类。

吹口锐边振动乐器上所用的空气柱因管的结构不同可分为开管与闭管两种，管的两端开口的叫做开管 （open pipe），一端关闭的叫做闭管 （closed pipe）。它们的振动特点亦有差异。

1.开管发音的振动结构之分析

两端开口的管叫开管。开管的开口处，空气由密入疏，空气分子的振动最为剧烈，其过程由开管空气柱的振动波从管的一端出发，到达管的另一端又被反射回来，当这个反射波回到原处后如果恰和下次振动所引起的波相位完全重合，就形成驻波，然后又一起向另一端出发，这时，波振动幅才能得到加强，获得最大音量。因此，开管空气柱在振动时，两端都是振动的波腹，在管的1/2处 （中段）是基频的波节，在管的1/4、3/4处形成第一泛音的节，在管的1/6和5/6，以及1/2处形成第二泛音的节……

由此可知，开管基频的波长等于管长的2倍，第一泛音的波长等于管长，第二泛音的波长等于2/3管长……， 它们的比例是 1∶1/2∶1/3……它们的音高分别是基音、高八度、高十二度和高两个八度等。因此，开管可以产生所有的奇数和偶数的泛音，即：可以发生所有的倍音。开管基础音频率公式可表示为：

f＝c/λ＝c/2L

其中，f＝基频，c/λ＝管中的声速/波长，L＝管长 （详见图3）。

图3中，a1表示1/2λ开管发生音时气柱振动的状态，中心1/2处为节点，两头的开口端各为波腹点；a2表明振动驻波有两个波节和三个波峰，显示2/2λ开管发生二倍音时气柱振动的状态；a3表明振动驻波有三个波节和四个波峰，显示3/2λ开管发生三倍音时气柱振动的状态；a4表明振动驻波有四个波节和五个波峰，显示4/2λ开管发生四倍音时气柱振动的状态 （倍数更多时不一一列举）。

2.闭管发音的振动结构之分析

一端开口而一端闭塞的管叫闭管。闭管空气柱振动时，其开口端是振动波的腹，而闭管末端的空气是不振动的，因此，闭端的空气对于空气柱的振动来说，这里永远是波的节。

对于闭管空气柱来说，它的振动波需要往返两次，才能使反射波与再次发生的波相位重合，其周期为4L/C。此外，闭管的空气柱振动还有一个特点，即：只能产生基础音上方的第二、四、六、八等偶数泛音，而不能产生基础音上方的第一、三、五、七、九等奇数泛音。因此，当闭管的空气柱振动时，其基础音上方的第二、四、六、八等偶数泛音的波节至波腹的长度比例分别是1∶1/3∶1/5∶1/7，它们的音高分别是基音、高十二度和高二个八度又大三度等。因此，闭管只能发生奇数次的倍音。

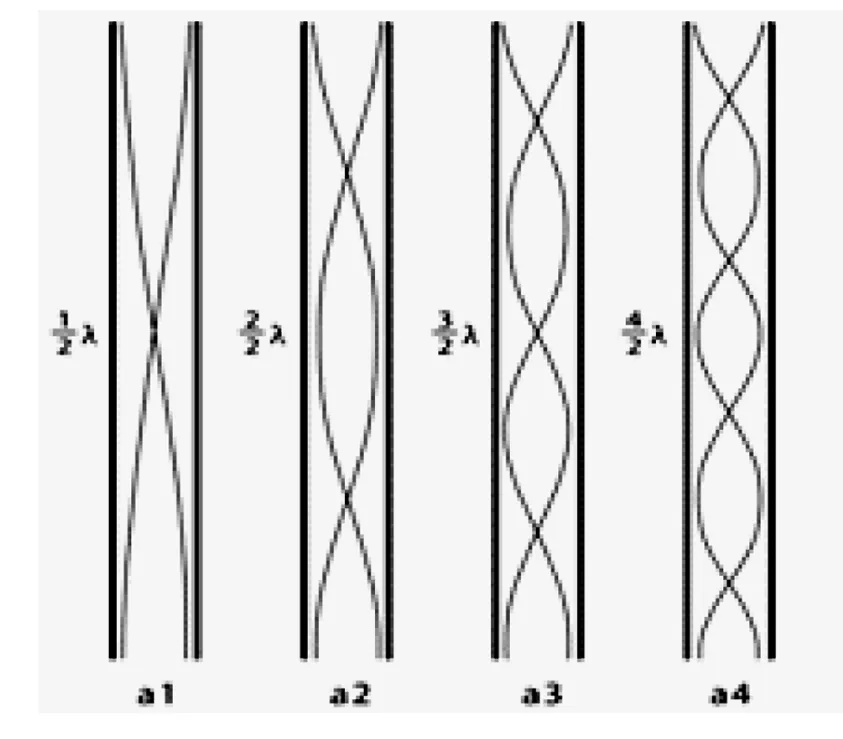
图3 开管空气柱振动示意图

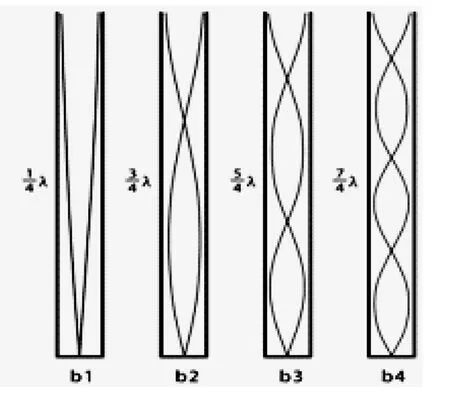
图4 闭管空气柱振动示意图

闭管基础音频率公式可表示为：

f＝c/λ＝c/4L

其中，f＝基频，c/λ＝管中的声速/波长，L＝管长 （详见图4）。

图4中，b1表示1/4λ闭管发生基音时气柱振动的状态，闭口端处为波节点，开口端处为波腹点；b2表示3/4λ闭管发三倍音时气柱振动的状态，显示出有两个波节和两个波腹；b3表示5/4λ闭管发五倍音时气柱振动的状态，显示出三个波节和三个波腹；b4表示7/4λ闭管发五倍音时气柱振动的状态，显示出五个波节和五个波腹。

我们从上两例所示的气柱振动状态的示意图中也可看到：在开管示意图中，每例的腹点至节点的长度，要比闭管示意图例中的短一半。所以，在一般情况下，对于同样材质、同样长度和同一围径的吹管来说，开管的固有频率比闭管的固有频率高一个八度。

此外，就内膛没有锥度、无节阻而相对均匀、平整的圆柱形律管而言，只有当细管管长在管内径的8倍以上，而粗管的管内径与管长之比值不超过1/40时，即在长短、粗细适当的情况下，上述的开管 （或闭管）的基础音频率公式才能适用。这是因为：“管中不仅有空气柱的纵向振动，即沿管长方向往返运动的纵波，还有沿管径方向振动的横波；当管子太细时，管中振动空气与管壁之间摩擦对空气振动的影响增加。摩擦的影响是使得空气的动能变成热能而消耗，最后造成管截面上各点运动情况有差异。通常，乐音是由管中空气柱振动的纵波所产生，在管子不过粗或不过细时，这种纵波才能被看作是沿管长方向的平面波，这时在管截面上各点的空气分子振动速度基本相同。”

缪天瑞先生在他所著 《律学》第一章导论中认为：“大多数的管乐器，如竹笛、双簧管和大管等的管子，都属于开管；中国的律管，排箫和福建南音中的福笛等吹管，都属于闭管。”

（四）吹口锐边振动的原理

就吹口锐边振动的原理而言，《声学手册》上告诉我们：“（边棱音），窄缝中冲击的喷注遇到正对着的棱时所发的声音。”就整个吹口锐边振动的过程而言，梁广程在 《乐声的奥秘》中告诉我们：“边棱音发声过程是这样的：当一股气流射向管口尖锐的入口处 （边棱）时，气流即分为两股，形成上下两列分离的涡旋，这时涡旋之间出现了空吸现象。由于管口的压强低于大气压而使两列涡旋相互吸引，产生碰撞而振动发声。”

此外，赵松庭在 《横笛频率计算与应用》一文中告诉我们：“笛，横吹的开管乐器，通过人体吹气并经过唇部的控制，使气流成一束，以斜面角度射入管的吹端，从而产生边棱振动，在管内形成驻波，发出与管长对应的频率。凡是属于这一类振动发声的都可称为笛。如果是加上簧片振动发音的，如笙、双簧管、单簧管，就不能称为笛。笛与箫可以不分，因为它们的振动原理一模一样，箫也是斜吹的，不然就不会发声。但是笛与管一定要分。单簧管与双簧管也一定要分，因为单簧管是闭管，而双簧管与唢呐就不一定要分，因为它们性质完全一样。音乐辞典上把单簧管称为 ‘竖笛’，这是概念模糊。为了尊重习惯，箫和笛子这两个概念可以拟竖吹和横吹来区分。凡是竖吹的，性质和笛子一样的乐器，我们称它为箫。凡是横吹的则称为笛子。”

赵松庭先生上述的对于笛子等吹口锐边振动过程的描述和界定，对我们认识竖吹但不开孔的律管有着触类旁通的积极意义。

（五）管律律种学之滥觞［4］

纵观我国古代管律律种的产生以及对它的发展史研究，至少已有八千多年了。古代律管在距今8000—7000年前的史前社会时期已初露端倪。

1984年10月，由时任河南省文物研究所第一研究室副主任的张居中带领考古队，前往河南舞阳县贾湖村新石器时代早期遗址，他们发现了一批骨笛 （见图5），用碳同位素14法①用碳同位素14法测定地层的年代是考古学研究上的专项测试技术，我国考古界于20世纪70年代从国外引进。其测定原理是，一切有生命的物体都含有碳元素，当其活着的时候，碳元素始终保持一定的数量，其死后，碳元素失去补充的来源，遂慢慢减少，其半衰期为5730年。所以只要测出有关地层中出土的含碳物体如木构件、稻谷、动物骨骸中碳元素含量，便可以计算出它死亡的年代，从而推断出它所在的文化层的绝对年代。测定，其形成年代距今约7800—9000年。

图5 贾湖骨笛

贾湖骨笛的形制有五孔、六孔、七孔、八孔等多种，其中包括：

1.前期五孔笛、六孔笛各 1支，距今约8600—9000年。

2.中期七孔笛16支 （其中2支已残，七孔不全），距今约8200—8600年。

3.晚期七孔笛2支、八孔笛1支 （余4支已残），距今约7800—8200年。

在这批骨笛中，中、晚期骨笛的笛孔口大都存有挖孔前留下的刻度。这些刻度表明，骨笛上的孔位并不是随意开挖的，而是先测算定位，然后按刻度开孔。不仅如此，有的骨笛还在开孔过程中对原设计的孔位一再修正 （见图6）。

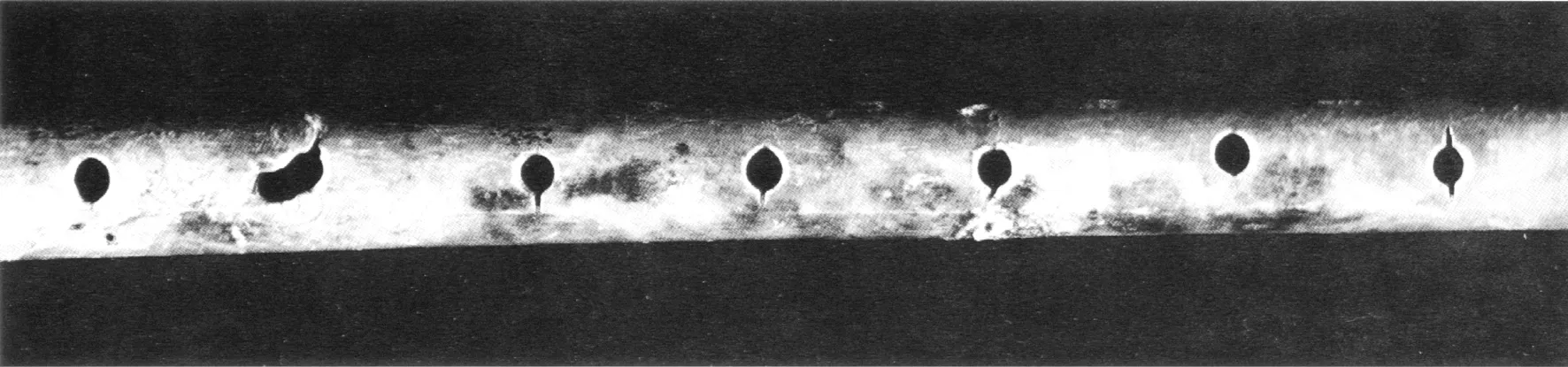
图6

而在这批骨笛中，出土编号M282：20（见图7）最完整。此笛有七个圆音孔，在第二、三、七孔旁有设计时留下的未钻透小圆点。第七孔上端开有一个小孔，可作调整第七音孔发音之用 （小孔的开或闭，会使第七孔音稍有高低的不同）。

图7

张居中和另外几位考古专家立刻带着最完整、最具代表性的M282号墓中的20号骨笛专程来到北京。他们首先找到了中国艺术研究院音乐研究所的萧兴华先生。萧兴华一见到这只骨器便大吃一惊。萧兴华说，骨管的构造与笛子尽管很相像，但有一个重要的不同，这就是骨管两端开口，没有吹孔。尽管骨管没有吹孔，但仍然是吹奏乐器。塔吉克族的鹰骨笛、哈萨克族的斯布斯额，都是用笛子的一端作为吹口的，只是吹奏时要将笛子斜持，使吹口与嘴唇形成45度的倾斜角，利用声波的震荡，使乐管的边棱发音。

尤其重要的是，至今还在河南民间流传的吹奏乐器竹筹，也是两端开口的。萧兴华当即便带着他们一行来到中央民族乐团找到刘文金团长。刘文金听了考古专家们的简单介绍之后，便召集管乐声部的好几位同志来试奏。笛子演奏家宁保生首先用斜吹的方法吹出了它的基本音阶，这一结果使所有在场的人都受到了很大的鼓舞。此后不久，萧兴华又和另外几个人携带stroboconn闪光频谱测音仪，专程前往郑州，对M282号墓中的20号骨笛进行了音序测试。

经测音得知，此笛的筒音和七孔音的大体音高如表4：

表4

萧兴华和另一位音乐研究者分别用斜吹的方法吹奏了上行和下行的音序，又分别吹奏了河北民歌《小白菜》的曲调，相当准确的音高和坚实而又嘹亮的音色，使在场的人都大为震惊。

之后，萧兴华又对下列骨笛进行了试吹：

1.M341∶1号五孔骨管：能吹出do mi sol la四声音阶。

2.M341∶2号六孔骨管：能吹出do re mi sol la五声音阶。

3.M282∶20号七孔骨管：能吹出do re mi sol la si六声音阶。

4.M253：4号八孔骨管：能够完整吹出do re mi fa sol la si七声音阶。

考古学家们锲而不舍，在贾湖遗址的三年里，分别采用释证、补证、参证、反证，以及吹管验声等方法互相参较进行考古工作，其精神令人钦佩。

河南博物院副院长李宏说：“人们习惯将中华文明起源与三皇五帝的传说时代联系起来。音乐的起源和乐器的发明也是这样。而距今近八千多年骨笛的出土，将整个中国音乐史的起源，由文献所记载的三皇五帝时的五千年提前了三千多年，改写了中华音乐文明起源时间，这是了不起的奇迹！”

（六）东晋荀勖的管口校正研究［3］294⁃297，310⁃313

古代律学基本上都是以弦长作为计算依据，故诸律制的律数，一般都适用于弦律。而律管的用途在于定标准音，在标准音确定之后，再用弦律计算，据弦律来定其他律管的音高。但因管是三维的空气柱振动，其实际长度并不等于管的实际长度，故在计算管乐器不同的音高所对应的管的长度时，必须把气柱的长度与管长之间的差数考虑在内，这个差数就是所谓的 “管口校正”数 （mouth correc⁃tion）。

东晋光禄大夫荀勖的 “管口校正法”是我国律学史上的一大成就。据 《晋书·律历志》（约630）的记载，东晋荀勖 （卒于289）曾于泰始十年制成十二笛以应十二律，他考证音律所得出的管口校正数是：一支律管的长度与另一较高四律的律管长度的差数。为此荀勖所制 “十二笛”的管长严格按 “三分损益法”计算，定 “黄钟”（C）为九寸，“黄钟”笛之长为四个 “姑洗”（e）之长（ ［9寸× （2/3） 2× （4/3） 2］×4＝寸），称“四角之长”，其他十一笛亦如此。但在笛上开六孔（一笛吹七音）时，荀勖发现，“黄钟”笛上的宫音（do）孔，不是距吹口为18寸，而是 “黄钟”（9寸）和 “姑洗”。

这说明荀勖已经发现了管身的长度不等于管内空气柱振动的长度，因此要作 “管口校正”，其校正数即 “黄钟”和 “姑洗”两律律数之差。他以这一原则制作了十二笛，而荀勖十二律笛之正声各有其对应律笛之笛体中声 （倍正），如：黄钟律笛之宫音 （宫穴到笛首的距离为1.611尺），与其对应的夷则之笛 （四角之长为0.9尺×4＝3.6尺）的笛体中声倍宫音为三分律八度关系，由3.6尺 ∶1.611尺，进一步推算它们之间的管长比，约为9∶4。

笔者分别整理了另外十一律笛之宫声与其对应律笛之笛体中声 （倍正）的管长，现一并列入下列表格中：

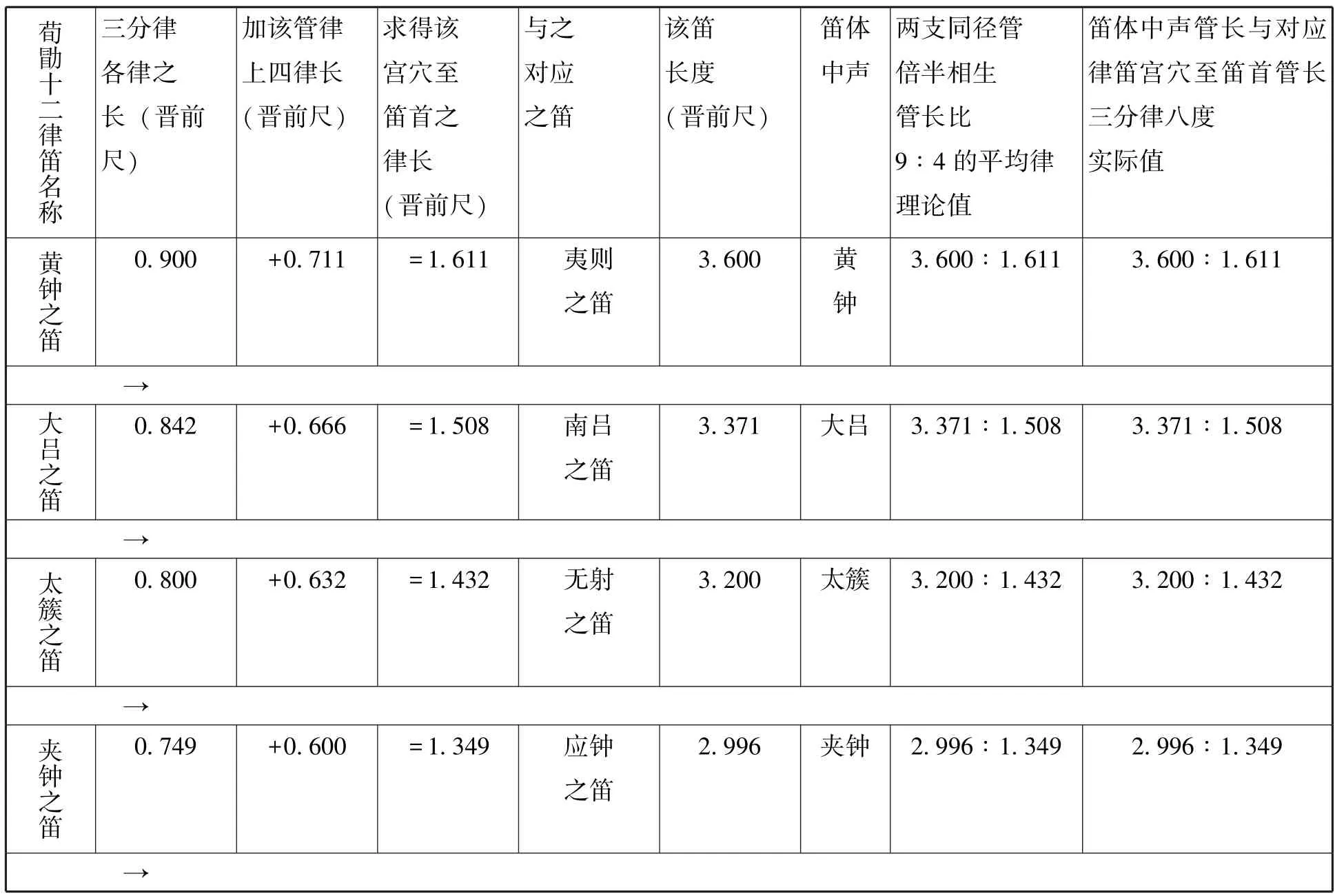
表5 荀勖十二律笛的各笛宫音与其对应笛之笛体中声9：4管长比分析表

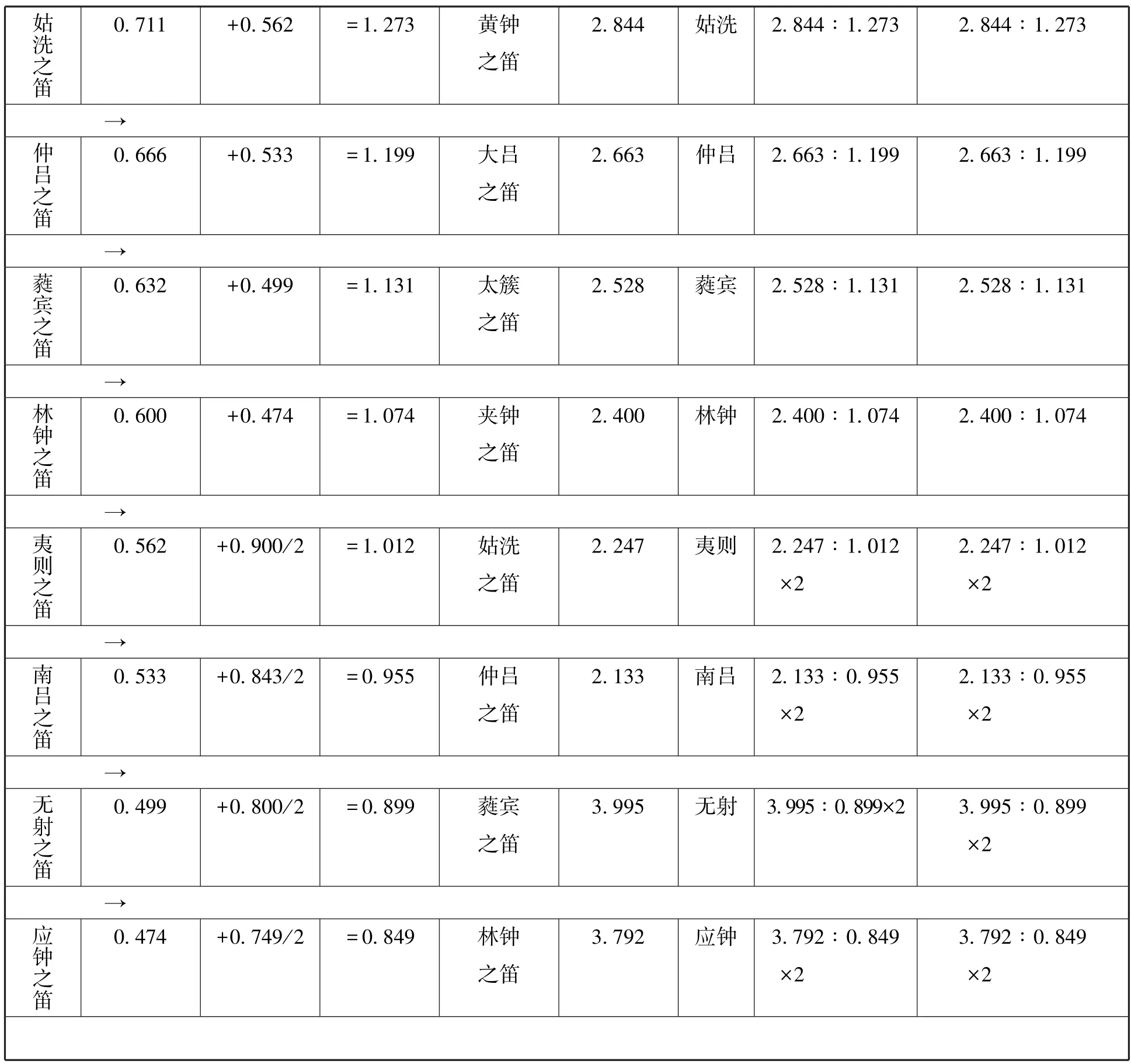
（续表）

这样，我们可以说，至少在公元289年以前，荀勖就已经创建了管律上的八度比值为9∶4。由于荀勖设计制作的律笛材料是 “下粗上细的自然之竹”，所以，荀勖在开笛孔时，还是借助了七弦琴作为辅助工具。因此，他的管律仍然是建立在弦律基础之上的。

为配合荀勖所创建的同径律管上八度比9∶4的经验值公式，笔者为探究9∶4的真相，曾制作了四组黄铜管律管，而后到声学实验室进行了验声。

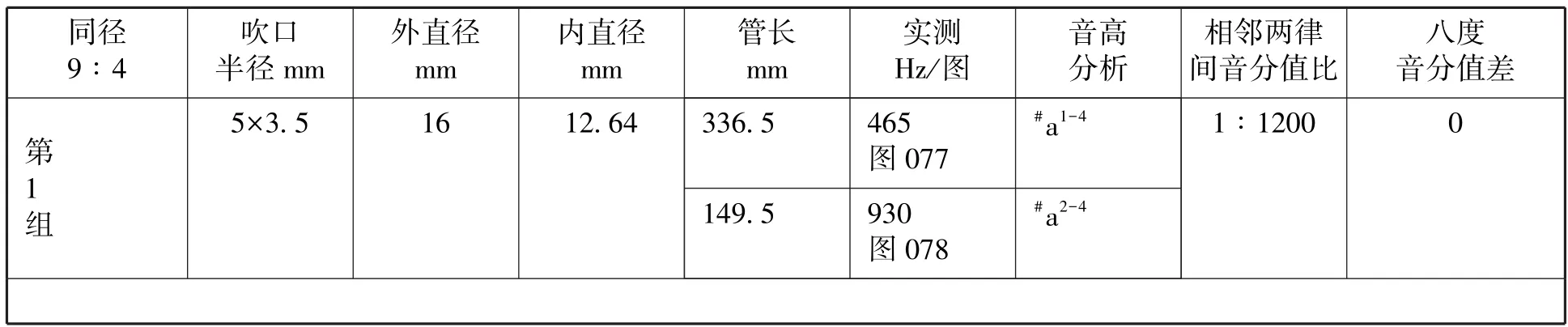
表6 四组8支黄铜管同径开管9∶4音高比较表 （室温24度）

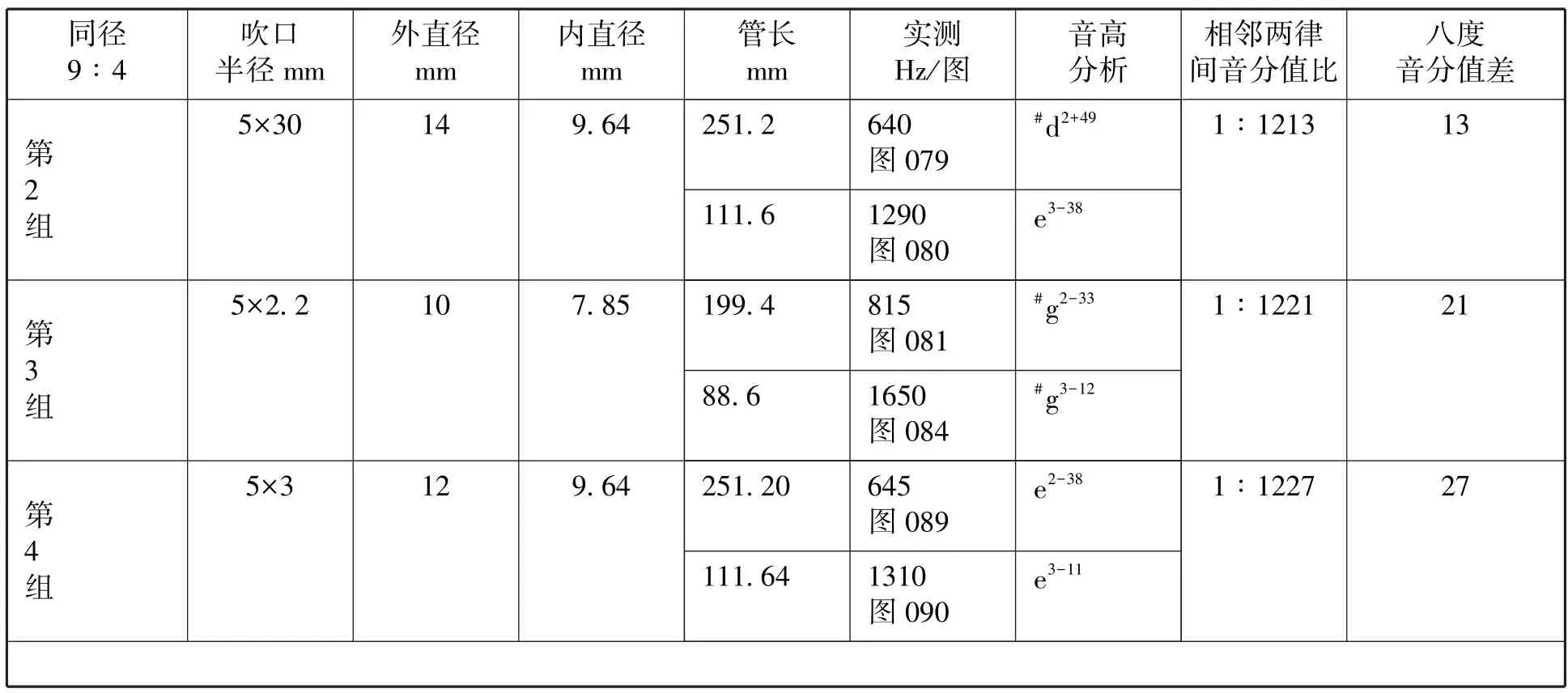
（续表）

（七）朱载堉的异径管律［5］

明代朱载堉在发明 “新法密率”（十二平均律）的同时，在 《律吕精义》一书中又提出了合乎十二平均律的 “异径管律”，以解决 “管口校正”的问题。

朱载堉从弦律研究中发现，弦上的不同音高变化，除了弦的长度不同之外，同样长度和松紧度的弦，若粗细不同，其所发出的音高亦不同。因此他认为管律除了注意管身长度之外，还必须注意管身的内径和外径。朱载堉对 “新法密率”的管律提出了两种最基本的生律方法：

3.朱载堉以二尺之长的律管作起点 （内径作2尺÷40＝ 0.05 尺， 外径作＝0.070771067尺），计算了三组共三十六根律管的长度、内径、外径等各种数值。实际上他只是在 “新法密率”弦律的基础上，用作为律管内径、外径的公比数，构成了三十六根律管之间的等比数列，以此来解决 “新法密率”管律中的 “管口校正”问题。

（八）鉴赏曲目

1.萧兴华用骨笛吹奏的河北民歌 《小白菜》；

2.《鹧鸪飞》（曲笛与乐队），演奏：张继良；

3.《三五七》（笛子独奏），演奏：陈涛；

4.福建南曲《八骏马》，据清咸丰七年（1857）厦门刊印的 《文焕堂初刻指谱》中称为《走马》定谱，福建泉州市南音团演奏。

三、钟律律种学之教学与鉴赏

1977年9月，解放军某空军雷达修理所因扩建厂房，偶然在湖北随县擂鼓墩发现了一座特大型古墓，从1978年5月11日开始发掘，至6月28日发掘结束，这座古墓后来经专家考证为战国时期即公元前433年5月3日落葬的曾侯乙墓。

曾侯乙墓共出土文物15000余件，其中乐器为9种125件。中室的编钟占据两面，编磬占一面，符合 “诸候轩县”的周朝等级制度规定。其中出土了一套共65件的编钟 （包括一件楚惠王赠送的镈钟），每钟可发二音 （42钟各发小三度音程，22钟各发大三度音程）。

65件编钟分三层、八组悬于钟架上。最上层是纽钟，共19件，分三组悬挂于上层3根横梁上。有甬 （长柄）者为甬钟，共45件，分中层三组、下层二组，各钟均刻有 “曾侯乙作持”铭文。

编钟音域宽广，达五个八度又一音，最低音是大字组的C，最高音是小字四组的d4，频率范围为64.8～2329.1赫兹，比现代钢琴高低音域各差一个八度。中心音域十二律完备，半音阶基本齐全。

现将分三层悬于钟架上共64件的八组 “合瓦形编钟”（每钟双音，左边音高指正鼓音，右边音高指侧鼓音）的实测音高列表7如下：

表7 八组编实测音高分析表 （各钟按钟架上从左向右的排列顺序分别列出音高）［1］47

在钟体下部正中部位敲出的音叫正鼓音，在钟体左右两侧敲出的音称侧鼓音，正鼓与侧鼓可单独发音，也可同时发音。

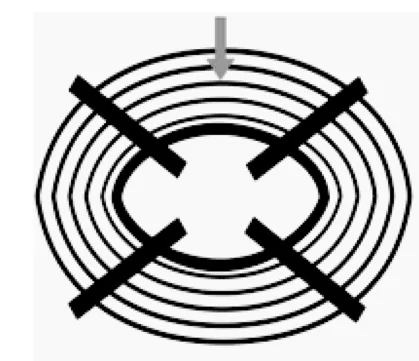
正鼓音振动模式

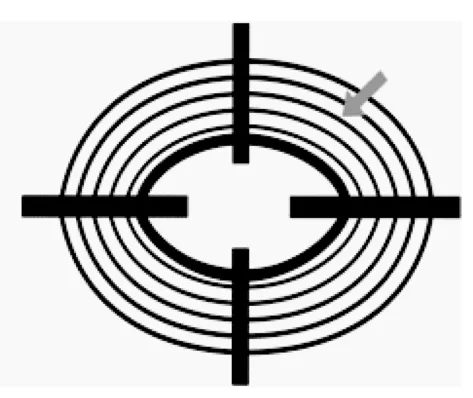
侧鼓音振动模式

正鼓音与侧鼓音构成大小三度的音程关系。如此奇妙的发音缘于编钟钟体不是360度圆，而是呈“合瓦形”的，敲击它的两个部位，可发出不同音高的频率，其声学原理以 “下层一组三钟的中间钟D～F” 为例：

当敲击正鼓部时，四根黑粗的节线 （即非振动区）在侧面，所击发出来的音频是正鼓音D；而当敲击侧鼓部时，四根黑粗的节线 （即非振动区）在正面，所击发出来的音频当然就是侧鼓音F了①详见中国唱片总公司出品 《曾侯乙墓·编钟》视频之激光实验报告。。

钟律律种学鉴赏曲目：

1.《楚商》（曾侯乙编钟与乐队），王原平编配，湖北编钟乐团演奏；

2.《屈原问渡》（曾侯乙编钟与乐队），王原平、黄讯舫编配，湖北编钟乐团演奏。

结 语

随着现代音响学和音乐声学等自然科学知识的普及，人们对于律学暨律种学的认识也在不断深化。我们知道，音由物体的振动而生，而物体振动的状态则根据振动物体 （包括发音体和共鸣体）的性质和形状等而各异。从我国周代根据制造乐器的材质 （金、石、土、丝、革、木、匏、竹）所确立的 “八音”分类法，到德国音乐学家萨克斯（Curt Sachs，1881—1959）依据乐器鸣响的振动性质所确定的分类法，它们分别是：弦鸣振动 （chor⁃dophone）、 气鸣振动（aerophone）、 膜鸣振动（membranophone）、体鸣振动 （idiophone） 和电鸣振动 （electrophone）等五大类。上述以发音体及其振动方式来区分的五大类，各有其自身的特点。

而中国古代的律学研究，如果从春秋时代管仲的 《管子·地员篇》开始算起，大约走过了两千八百多年的历程，无论是在中国古代文献中，还是在音乐考古发现中，弦律、管律和钟律等仨律种学都留下了它的轨迹。

难能可贵的是，历代乐律学家在当时并无任何测音仪器的情况下，他们 “以耳齐其声”，凭着顽强的毅力、不厌其烦的相较比对和数学运算，创造了音乐声学上的奇迹。在这个过程中，出现了七弦琴这一乐器，开创了对于自然律的研究，制定了徽法律；而后朱载堉发明了 “十二平均律”；由于对律管的应用，导致了荀勖对于 “十二笛律”的“管口校正”研究和朱载堉对于异径管律的探究；而作为铸造于公元前433年的艺术瑰宝，64枚编钟以其精湛的铸造工艺和非凡的音乐性能，显示了二千四百五十年前的古人在乐器制作上的创造：每枚“合瓦形”钟能击发出相隔三度的两个音，十二个半音齐全，而且有跨越五个八度又一音的 “钢琴”音域，并可以自如地转调奏乐，它那细微的音色变化和钟鼓齐鸣的合奏形式，以及钟体上二千八百多字内容丰富的错金篆体乐律铭文，再一次证明了曾侯乙编钟不仅是楚文化民族乐器中的典型代表，更是华夏音乐源远流长的象征。

在19世纪，英国音乐学家埃利斯 （A.Ellis，1814—1890）在比较诸民族的音阶时，首创了音分制。他把一个八度分成1200音分单位，是根植于十二平均律基础之上的，埃利斯把十二平均律细化成1200音分，从而使人们可以用这种音分制来量度各种各样的律制。

整个教学过程由于音乐声学数据和图片翔实、具象，CD和视频等声像资料充分，不但培养了学生的逻辑思维能力，也培养了他们的社会情感 （即道德和审美情感），使学生在仨律种学的音乐声学体验中，不断深化 “文化自觉”①已故社会学家费孝通先生在其译著 《文化论》的 “总绪论”中强调指出：“生活在一定文化中的人对其文化应有自知之明”，要 “明白它的来历，形成的过程，所具有的特色和它发展的趋向”，即 “提高 ‘文化自觉’的理性程度”，他呼吁：“在21世纪，我们需要更多的 ‘文化自觉’”。摘自 ［英］马凌诺斯基《文化论》，费孝通译，北京：华夏出版社，2002年，第3页。的观念，亦使他们的心理状态由 “注意”到 “发散”，再到 “集中”，有利于他们张弛结合、消除疲劳，提高了六个课时的教学效果。

［1］陈应时，陈聆群.中国音乐简史 ［M］.北京：高等教育出版社，2006.

［2］陈应时.琴律学 ［M］.上海：上海音乐学院出版社，2015.

［3］胡企平.中国传统管律文化通论 ［M］.上海：上海音乐出版社，2003.

［4］张居中.考古新发现——贾湖骨笛 ［J］.音乐研究，1988（4）.

［5］朱栽堉.律吕精义·内篇：卷二 ［M］.冯文慈，点注.北京：人民音乐出版社，1998.

（责任编辑：黄向苗）

Teaching Design of Temperament and Temperament Species of Ancient Chinese Music History

HU Qiping

In the teaching of Ancient Chinese Music History for the musicology major in Chinese universities， the cognitive characteristics and patterns of college students should be considered in the teaching unit of Temperament and Temperament Species．Concerning with the teaching characteristics and methods of musical acoustics， ancient musicians’ exploration and research results are sorted out about chordophone，aerophone and idiophone with mathematical means under the background of the music culture of“tuning by ear”.Combined with research achievements on ancient music archeology since the reform and opening up，the teaching is carefully designed as three lesson plans within six class hours.

temperament； temperament species； music acoustics； ancient Chinese music history

J612.1

A

1672⁃2795 （2017） 02⁃0037⁃14

2017－02－02

胡企平 （1953— ），男，上海人，澳门理工学院音乐课部教授，音乐学博士，主要从事中外音乐史学、律学暨管律律种学的教学与研究。（澳门 999078）