间日疟疫情与气象因素的广义相加模型研究

郑金鑫，史本云，杨国静,4,5

间日疟疫情与气象因素的广义相加模型研究

郑金鑫1,2，史本云3，杨国静1,2,4,5

目的探讨云南省腾冲地区疟疾疫情与气象因素之间的关系，以解释气象因素在疟疾传播与流行中的作用，为采取针对性的预防措施提供理论依据。方法根据中国疾病预防控制中心提供的2005-2010年腾冲县间日疟月发病数据以及收集同期该地月平均气温、月平均最高气温、月平均最低气温、月降雨量、月平均相对湿度、月最小相对湿度等气象资料，运用Pearson相关分析方法分析疟疾发病例数与气象因素的相关性，采用广义相加模型分析气象因素及媒介能量与疟疾发病之间的关系。结果最低气温、平均相对湿度及最小相对湿度与本地疟疾发病间存在较弱的正相关关系；媒介能量、相对湿度与疟疾发病间存在较复杂的非线性关系。当媒介能量>10时，呈现正效应，并随媒介能量的增加对疟疾发病的正效应逐渐增强；当平均相对湿度在55%～70%之间时，对疟疾发病产生正效应，但相对湿度>70%时，对本地疟疾发病的效应值降低。结论广义相加模型能够较好地解释气象因素与本地疟疾发病之间的关系，媒介能量、相对湿度与疟疾疫情间存在着较为复杂的非线性关系。

疟疾；广义相加模型；气象因素；媒介能量

疟疾是严重危害人类身体健康和生命安全、影响社会经济发展的重要寄生虫病之一，约50%的世界人口面临着感染疟疾的风险[1]。当前我国疟疾的发病主要集中在海南、云南等地区。2009年云南省共报告疟疾病例3 163例，疟疾发病率0.69/万，输入病例占70.22%，发病率超过1/万以上的县占15.50%[2]。为积极响应全球消除疟疾行动，我国政府于2010年提出了国家消除疟疾行动计划，提出“到2015年，全国除云南部分边境地区外，其他地区均无本地感染疟疾病例；到2020年，全国消除疟疾”的目标[3]。疟疾的传播与流行与气象因素密切相关，已有文献证实气温、降雨量等对疟疾的发生影响较大[4-6]。近年来，广义相加模型(Generalized Additive Model,GAM)已经广泛应用于公共卫生领域[7-8]， GAM 是广义线性模型的非参数扩展[9]，适用的范围更广，常用于处理应变量和众多解释变量间过度复杂的非线性关系，并图示出变量间的非线性关系。随着中国疟疾消除计划的实施，逐渐完善的监测体系为疟疾的预防与控制奠定了坚实的基础，若能结合广义相加模型发现影响疟疾疫情的因素，并确定各种因素在某一阶段水平的变化对疟疾疫情产生的效应值，对制定防控决策具有重要意义。因此，本项研究以云南省腾冲县间日疟发病数为例，应用广义相加模型研究气象等因素对疟疾发病疫情的影响特点与规律，为控制与消除疟疾提供科学依据。

1 资料与方法

1.1 研究区域 选择云南省腾冲县作为研究区域，由于地处中缅交界处，属亚热带气候，每年都有输入性疟疾病例的发生，是云南省疟疾高发地区，也是全国疟疾重点监测点之一。

1.2 资料来源 该地区间日疟月发病数据来源于中国疾病预防控制中心，资料收集的时间段为2005-2010年，同期的气象资料来源于中国气象科学数据中心，其中气象资料包括平均气温、最高气温、最低气温、平均相对湿度、最小相对湿度、降水量等。

1.3 统计方法

1.3.1 数理统计 对2005-2010年期间腾冲县本地间日疟月发病例数及气象因素的特征采用描述性分析研究；疟疾疫情与气象因素间的相关性采用Spearman相关性分析，该研究的检验水准统一取值0.05。所有统计分析均在R3.3.1软件中完成。

1.3.2 媒介能量 本研究采用媒介能量来表示降雨及温度对蚊媒传播疟疾的影响，根据Pietro Ceccato[10]提供的公式，依据温度及降水量2个气象变量计算出媒介能量(Vectorial Capacity VCAP)，该指标与疟疾的传播与流行密切相关。

1.3.3 广义相加模型及其建立 GAM最早由 Hastie和 Tibdhirsani 在1986年提出[9]，是对传统广义线性模型的扩展，广义相加模型一般形式：

g(μ)=β+f(Xi1+f(Xi2)+…+f(Xip)+ε

①

其中g(μ)代表各种连接函数关系，可以是多种概率分布，包括正态分布、二项分布、Poisson分布、负二项分布等；f(Xip代表各种平滑函数，如光滑样条平滑(Smoothing Spline，SS)、局部回归平滑(Local Regression，Loess)、自然立方样条(Natural Cubic Spline，NS)、B样条(B Spline，BS)和多项式等。

log[(Yt+X)]=α+s(vt,df)+βvt

②

其中，Yt为月疟疾发病数；对于每个t,Yt服从总体均数为的Poisson分布；log[(Yt+X)]为月疟疾发病数期望值；α为截距；vt为所纳入的自变量，有平均气温、 最高气温、最低气温、平均相对湿度、最小相对湿度、降水量及媒介能量；β为回归模型系数；将单个变量代入方程，根据t值与F值，判断是否为线性部分与非线性部分；其中非参数的形式为平滑样条法，平滑参数的估计选择交叉验证法。建立分模型通过计算赤池信息量准则(Akaike Information Criterion, AIC)、贝叶斯信息准则(Bayesian Information Criterion, BIC)以及均方误差(Mean Square Error, MSE)筛选出最优模型。

2 结 果

2.1 描述性分析 2005年1月至2010年12月腾冲地区本地间日疟发生的总病例数为1 480例，呈逐年下降趋势，有明显的短期波动，每年夏季病例数都会增多。见图1。气象基本信息见表1。

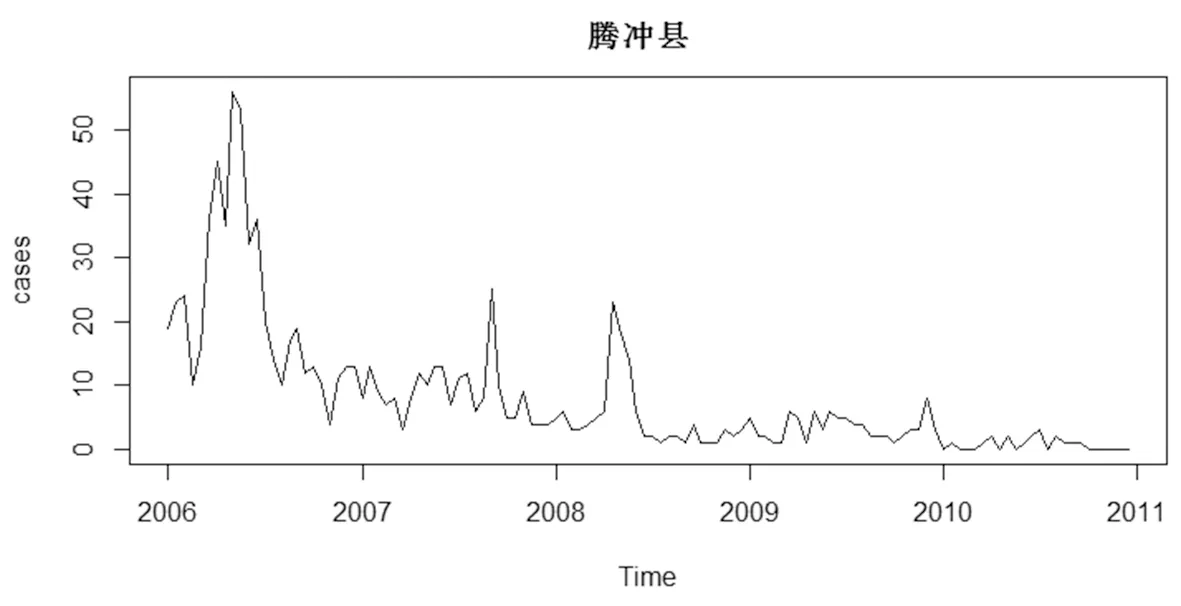
图1 2005-2010年腾冲县本地间日疟发病病例数Fig.1 Monthly local malaria cases from 2005 to 2010 in Tengchong County, Yunnan

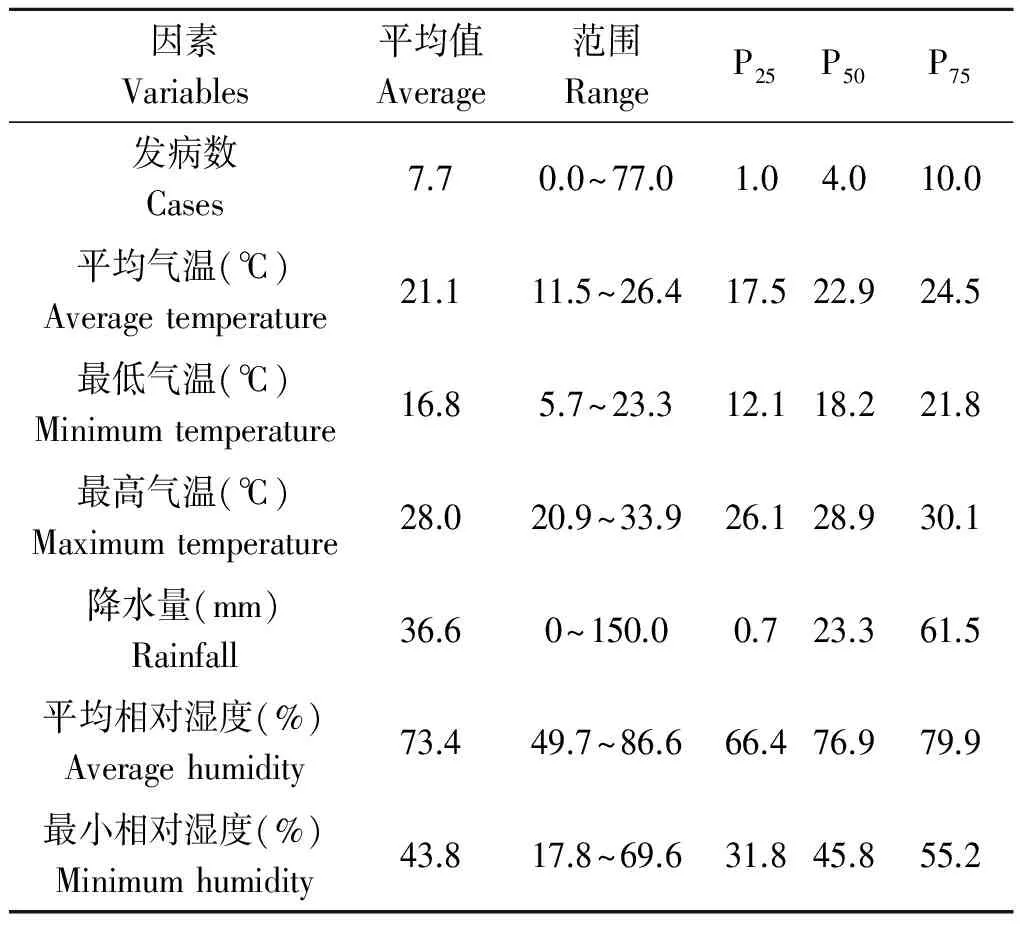
表1 2005-2010年腾冲县本地间日疟发病与气象因素基本信息Tab.1 Description of monthly local malaria and meteorological factors from 2005 to 2010 in the study area

2.2 Spearman相关分析 对研究期间以月为单位

发生的疟疾病例数与气象因素之间进行Spearman相关分析，其中本地间日疾月发病例数与最低气温、平均相对湿度及最小相对湿度存在较弱的正相关关系(P=0.070，接近0.05)，与其他气象因素间的无相关关系(P>0.05)，提示可能存在较复杂的非线性关系，见表2。

2.3 GAM分析 初步非参数GAM分析显示，最高气温、降水量以及最小相对湿度与本地疟疾发病不存在线性相关，而在GAM非线性结果中，平均气温、最低气温及平均相对湿度有统计学意义，提示在建立合适方程时，应入选相应变量(见表3)。因而考虑从单个变量开始进入方程到全部变量入选，其中包括线性与非线性模型(见表4)。

依据AIC，BIC与MSE值判断，最优模型为非线性的log转换模型(表2)，而含有VCAP变量的模型为最佳模型，可解释45.8%的本地疟疾的发生，气象因素中相对湿度与疟疾的发生存在复杂的非线性关系，是非典型的直线相关关系。而采用典型直线相关模型(表2第2行)亦可解释33.4%的本地疟疾发生，但在模型中降水量在方程中无统计学意义(P>0.05)。

上述结果中降雨量对疟疾发病为阴性，为进一步探究降雨量、温度与疟疾发病的关系，考虑到疟疾发病率逐年递减趋势，根据公式(2)将降雨量与温度转换成VCAP变量，其中VCAP与相对湿度都为非线性部分，建立GAM模型(表2第5行)VCAP(F=11.76,P<0.01)与平均相对湿度(F=8.05,P<0.01)在方程中均有统计学意义。如图2本地疟疾发病与气象因素关联的效应图。VCAP变量与本地疟疾发病呈现出非线性关系，当VCAP>10时，呈现正效应，即随VCAP增加正效应增强；而平均相对湿度与本地疟疾发病却显现出复杂的非线性关系。当平均相对湿度处于55%～70%之间时是正效应，而当相对湿度>70%时，对本地疟疾发病的效应值降低。

表2 气象因素与本地间日疟发病例数相关性分析(n=96)Tab.2 Correlations between malaria cases and meteorological factors (n=96)

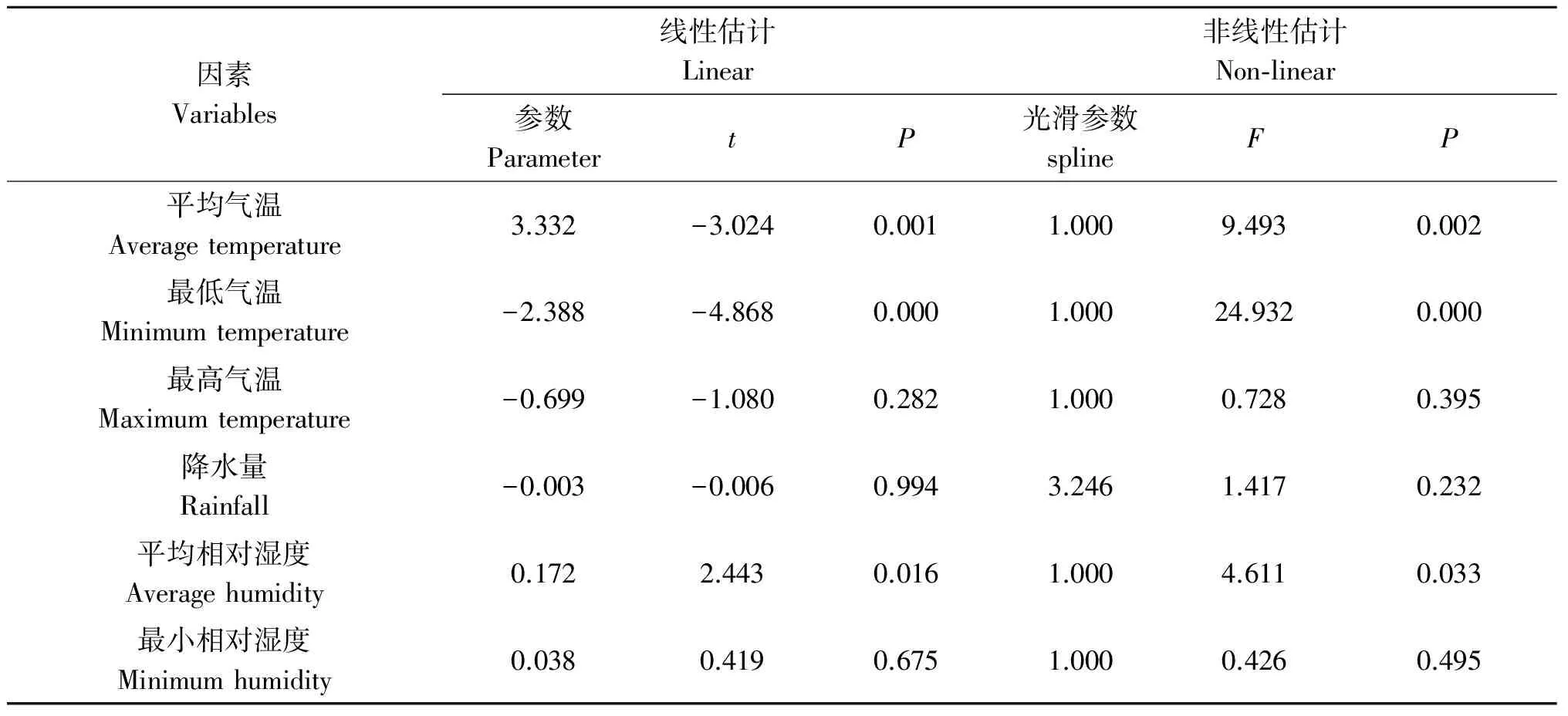
表3 GAM分析结果Tab.3 Results of linear and non-linear GAM model

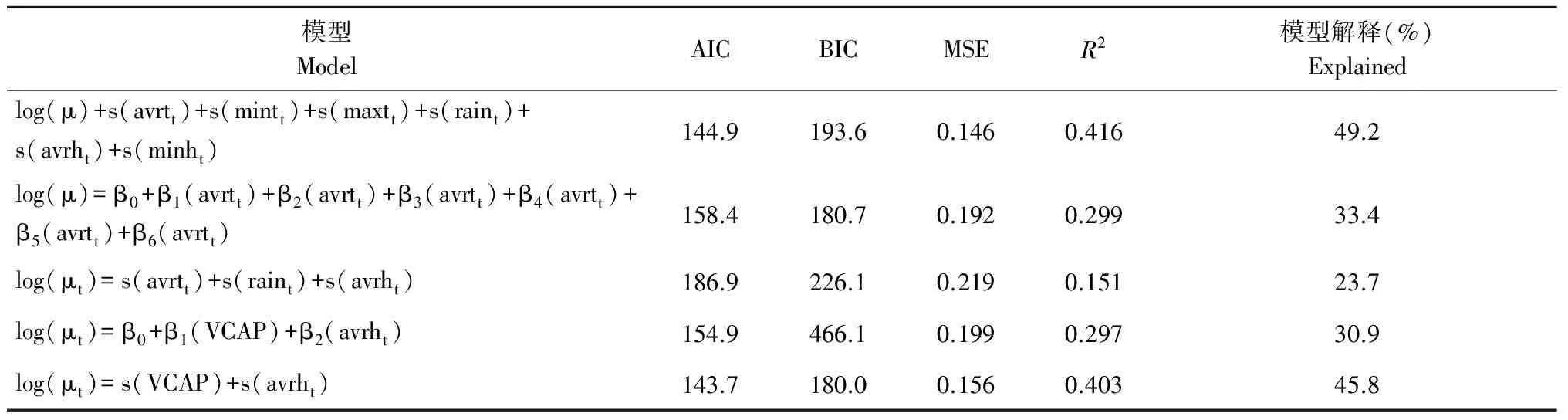
表4 GAM线性与非线性模型Tab.4 Linear and non-linear GAM model

注：avrt-气温、mint-最低气温、maxt-最低气温、avrh-最平均相对湿度、minh-最小均相对湿度、rain-降水量、VCAP-媒介能量，μt为t月份本地疟疾发病病例数的期望值。

Note: avrt-average temperature, mint-minimum temperature, maxt-maximumu temperature, minh- minimum humidity, rain- rainfall, VCAP-Vectorial Capacity,μt-expected of local malaria cases in t month

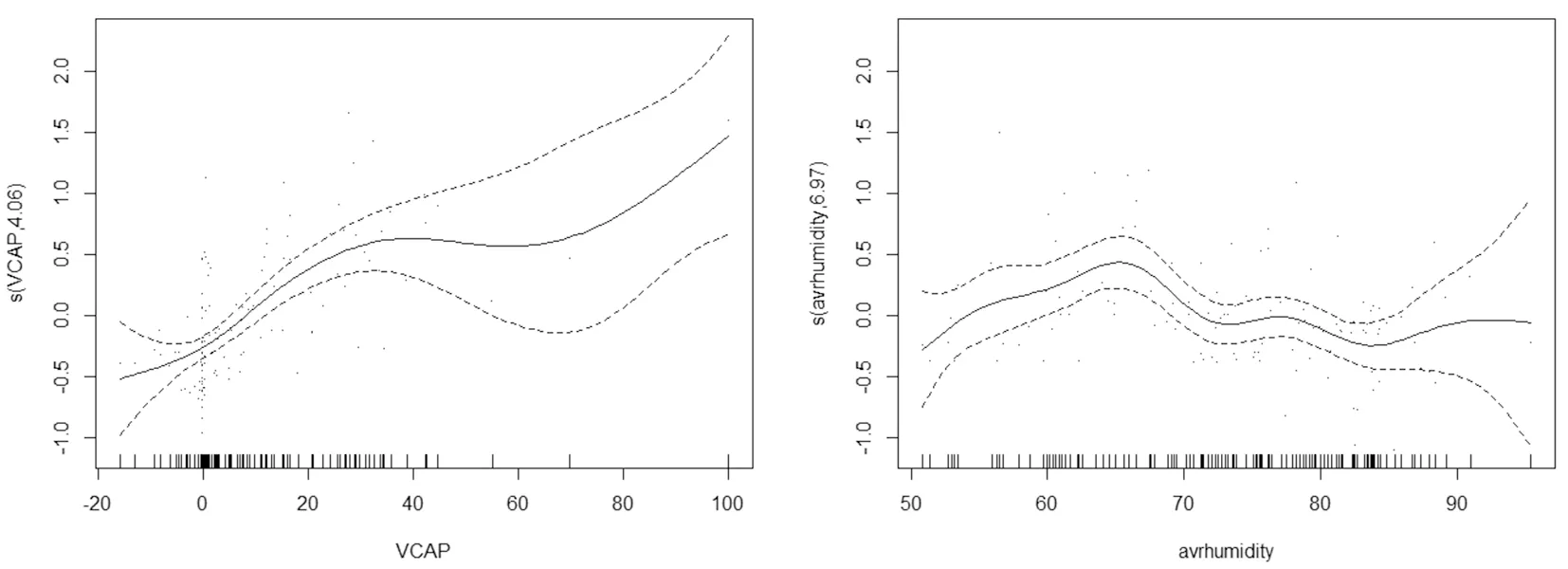
注：VCAP表示媒介能量，avrhumidity表示平均相对湿度Note:VCAP-Vectorial Capacity, avrhumidity-average humidity图2 本地间日疟发病与气象因素关联的效应图Fig.2 The effect of local malaria incidence and meteorological factors

3 讨 论

广义相加模型在公共卫生领域的应用广泛，同时间序列分析一样，结合了时间序列数据中的长期趋势和短期波动，在控制了影响因素的基础上，可通过参数与非参数拟合气象因素对疟疾发病的影响。该方法可以很好地对非线性关系进行拟合，可适用于任意分布类型的资料，且构建的模型较为灵活。虽然疟疾流行的高危区域同时存在间日疟与恶性疟，但间日疟占发病数的主体地位，例如，有研究指出中缅边境地区间日疟占79.3%,恶性疟占20.1%[11]，2011年数据显示输入性病例中间日疟占73.59%[12]，但腾冲县的间日疟疫情还有待于进一步研究。随着中国消除疟疾计划实施的不断深入，作为国家重点监测与防控地带，云南地区间日疟的流行与传播规律及其影响因素的研究在全国疟疾的防治工作中具有极为重要的战略意义。

本文采用广义相加模型探究气象因素与本地疟疾发病之间的关系，计算各气象因素与本地疟疾发病之间的线性与非线性关系，比较不同气象因素组成模型的AIC、BIC以及MSE值等，寻找合适的模型，探究最优模型中变量间的作用关系。GAM结果显示，VCAP及平均相对湿度与本地疟疾发病之间存在非线性关系，而最终优选模型仅含VCAP与相对湿度2个变量。研究显示平均相对湿度处于55%～70%之间时，便于疟疾的媒介的传播。有研究结果显示相对湿度达到60%以上，则可引起疟疾的传播与流行[13]，表明相对湿度是影响疟疾传播的一个重要因素。随着相对湿度的增加，疟疾发病的累积相对危险度先增加后减少，当相对湿度为62%且滞后10周时的累积效应最大。此次研究结果也显示相对湿度在55%～70%之间对本地疟疾发病的效应值为正向作用，提示适合蚊类的滋生的气候环境一般较温和，但相对湿度过高可能不利于媒介的生存。VCAP是将降水量信息与温度数据结合综合反映疟疾传播效应的指标，是早期疟疾发病监测的标志性指标，能够在疟疾监测系统里发挥很重要的作用[10, 14]，本次研究显示VCAP与本地疟疾发病呈现出非线性关系，在VCAP>10时，可增加疟疾发病的风险，也再次证明VCAP在腾冲地区发病的监测具有一定的导向作用，这与广东省的研究结果一致[15]，将媒介能量作为疟疾传播强度的指标,为控制疟疾暴发流行提供科学依据。

气候因素对疟疾传播的影响较为复杂，可能引起蚊虫媒介的生活习性改变，既当天的气温及湿度对蚊虫媒介的影响可能延迟至第二天，致使疟疾病例的发生与气象因素之间存在一定的滞后效应[16]，而本次研究未考虑气象因素对疟疾发病的滞后效应，有待进一步的完善。本次研究数据显示，腾冲县疟疾发病的高峰集中在2007年之前，随着政府对疟疾监测与防控力度逐步加大，疟疾发病率逐渐降低，其中人为干预因素是最主要的原因。为使模型更具有代表性，需考虑到人为干预因素。另外，该区域处于云南与缅甸毗邻地带，流动人口数量较大，以输入性病例为主[17]，且每年4-5月份都有大量劳动人口回流[18]，提示人口的流动具有一定的周期性。而本次研究未将上述因素考虑在模型中，这也是将来研究的重点，使得模型预测与拟合更加精确，更接近真实情况。本次研究的重点为间日疟，后续还将对恶性疟进行分析，探究两者之间的异同性，不断完善优化疟疾的防治工作。

综上所述，GAM能够较好地分析并解释气象因素与本地疟疾发病之间的关系，气象因素是疟疾发病的影响因素之一，且VCAP在本地疟疾的发生上具有一定程度的可解释性，相对湿度与疟疾的发病存在着较为复杂的非线性关系。应用GAM能很好地发现疟疾发病的影响因素，但气象因素只是众多影响因素之一，今后的研究还需要结合其他影响因素如社会经济学因素、人口流动因素等，建立更为准确和完善的模型，优化科学有效的防治措施，顺利实现云南地区疟疾消除的计划目标。

[1] WHO. World Malaria Report[Z]. 2014.

[2] Li HX, Chen GW, Yang YC, et al.Epidemiological study of malaria in Yunnan province, China from 2001 to 2010[J]. Chin J Vector Biol Control, 2013,24(2):147-151.DOI:10.3969/j.issn.1000-7423.2008.01.010(in Chinese)

李华宪，陈国伟，杨沅川，等. 云南省2001-2010年疟疾流行现状与趋势[J].中国媒介生物学及控制杂志,2013,24(2):147-151.

2.1 地塞米松组和对照组术后视力改善情况 地塞米松组术后1 d视力提高率高于对照组(P<0.001)，两组术后1周视力提高率比较差异无统计学意义(P>0.05)。见表1。

[3] Cao J, Zhou SS, Zhou HY, et al. Malaria from control to elimination in China: transition of goal, strategy and interventions[J]. Chin J Schistosomiasis Control,2013,25(5):439-443.(in Chinese)

曹俊，周水森，周华云，等. 中国疟疾从控制走向消除——消除阶段的目标策略和措施[J].中国血吸虫病防治杂志,2013(05):439-443.

[4] Gao CY, Xiong HY, Yi D, et al. Study on meteorological factors-based neural network model of malaria[J].Chin J Epidemiol, 2003,24(9):831-834.DOI:10.3760/j.issn:0254-6450.2003.09.021(in Chinese)

高春玉，熊鸿燕，易东，等.智能神经网络模型用于气象因素对疟疾发病影响的初步研究[J]. 中华流行病学杂志,2003,24(9):831-834.

[5] Yang GJ,Yang K,Zhou XN.Assessment models for impact of climate change on vector-borne diseases transmission[J].Advances In Climate Change Research,2010(04):259-264. DOI:10.3969/j.issn.1673-1719.2010.04.005(in Chinese)

杨国静，杨坤，周晓农.气候变化对媒介传播性疾病传播影响的评估模型[J].气候变化研究进展,2010(04):259-264.

[6] Zhang BG, Zhang CL, Bo XQ, et al.Multiple stepwise regression analysis on relationship between malaria incidence and meteorological parameters in malarious area in Shandong Province[J]. Chin J Zoonoses,2013(03):257-261.(in Chinese)

张本光，赵长磊，卜秀芹，等. 山东省疟疾高发地区发病率与气象因子的多元逐步回归分析[J]. 中国人兽共患病学报,2013(03):257-261.

[7] Yi CH,Wang SG, Yin L, et al.Application of generalized additive models in the analysis of the relationship between daily trauma emergency department visit number and meteorological factors: a time-series analysis[J].J Lanzhou Univ(Nat Sci),2015(05):671-675.DOI:10.13885/j.issn.0455-2059.2015.05.013(in Chinese)

冀翠华，王式功，尹岭，等. 广义相加模型在创伤急诊人次与气象要素时间序列相关分析中的应用[J].兰州大学学报(自然科学版),2015(05):671-675.

[8] Tao FF, Zhao NQ, He C, et al. Application of generalized additive model in early warning of bacillary dysentery [J].Chinese Journal of Health Statistics,2012，(04):481-483.DOI:10.3969/j.issn.1002-3674.2012.04.004(in Chinese)

陶芳芳，赵耐青，何懿，等. 广义相加模型在细菌性痢疾预警中的应用[J].中国卫生统计,2012,(04):481-483.

[9] Li HT, Yuan Y, Li ZW, et al. An introduction of GAM in identifying non-linear correlations and its application in statistical modeling[J].Chin J Health Statistics,2012(06):782-785.(in Chinese)

李宏田，袁悦，李智文，等. GAM识别非线性相关及其在医学统计建模中的应用[J].中国卫生统计,2012(06):782-785.

[10] Ceccato P, Vancutsem C, Klaver R, et al. A vectorial capacity product to monitor changing malaria transmission potential in epidemic regions of Africa[J]. J Trop Med, 2012, 2012: 595948.

[11] Li BF, Lin YX, Guo XR, et al. Survey on malaria epidemics in China-Myanmar border area[J].Chin J Parasitol and Parasit Dis,2015(04):261-263.(in Chinese)

李奔福，蔺应学，郭祥瑞，等.中缅边境疟疾流行情况调查[J].中国寄生虫学与寄生虫病杂志,2015(04):261-263.

[12] Xia ZG, Yang MN, Zhang SS, et al. Epidemiological analysis of the imported malaria cases in China 2011[J].Chin J Dis Control Prevent,2014(03):226-230.(in Chinese)

夏志贵，杨曼尼，张少森，等. 2011年全国输入性疟疾病例流行病学分析[J].中华疾病控制杂志,2014(03):226-230.

[13] Kelly-Hope LA, Hemingway J, Mckenzie FE. Environmental factors associated with the malaria vectorsAnophelesgambiaeandAnophelesfunestusin Kenya[J]. Malar J, 2009, 8: 268.

[14] Macdonald G. Theory of the eradication of malaria[J]. Bull World Health Organ, 1956, 15(3-5): 369-387.

[15] Pan B, Chen XG, Wu J, et al. Compare the capabilities of malaria transmission betweenanophelesanthropophagusandanophelessinensisin Guangdong Province[J]. J Trop Med, 2008(11):1169-1171.DOI:10.3969/j.issn.1672-3619.2008.11.021(in Chinese)

潘波，陈晓光，吴军，等. 广东省嗜人按蚊与中华按蚊疟疾传播强度的比较[J].热带医学杂志,2008(11):1169-1171.

[16] Xia Q, Cai XX, Lin W, et al. Relationship between morbidity of malaria infection and meteorological factors in Hubei province from 2004 to 2009[J]. J Trop Med,2016(07):937-940.(in Chinese)

夏菁，蔡顺祥，林文，等. 湖北省2004-2009年疟疾发病率与气象因素关系[J].热带医学杂志,2016(07):937-940.

[17] Yin SQ, Feng J, Xia S, et al.Epidemiological analysis of imported malaria cases in 20 counties at border region of Yunnan Province from 2012 to 2014[J]. Chin J Schisto Control,2016(03):252-257.DOI:10.16250/j.32.1374.2016105(in Chinese)

尹授钦，丰俊，夏尚，等. 2012-2014年云南省边境地区输入性疟疾病例流行特征分析[J]. 中国血吸虫病防治杂志,2016(03):252-257.

[18] Duan ZY,Li SG, Kang XH,et al. Analysis of the prevalence of malaria in Tengchong County,Yunnan Province from 2005 to 2010[J].J Pathog Biol,2011(07):533-535.DOI:10.13350/j.cjpb.2011.07.020(in Chinese)

段义忠，李胜国，康显虎，等. 2005-2010年云南省腾冲县疟疾疫情分析[J].中国病原生物学杂志,2011(07):533-535.

Yang Guo-jing, Email: guojingyang@hotmail.com

GeneralizedadditivemodelofPlasmodiumvivaxmalariaincidenceandmeteorologicalfactors

ZHENG Jin-xin1，2, SHI Ben-yun3, YANG Guo-jing1,2,4,5

(1.JiangsuInstituteofParasiteDiseases,Wuxi214064,China; 2.PublicHealthResearchCenterofJiangnanUniversity,Wuxi31412,China; 3.HangzhouDianziUniversity,Hangzhou310018,China;
4.DepartmentofEpidemiologyandPublicHealth,SwissTropicalandPublicHealthInstitute,Basel40.,Switzerland; 5.UniversityofBasel,Basel40.,Switzerland)

This paper aims to find out the impacts of meteorological factors on malaria transmission by exploring the relationship between monthly local malaria cases and meteorological factors in Tengchong county, so as to develop malaria control strategy.Plasmodiumvivaxmalaria incidence data and meteorological data including monthly mean temperature, maximum temperature, minimum temperature, rainfall, relative humidity, and minimum humidity in Tengchong County, Yunnan from 2005 to 2010 were provided by the Chinese Center for Disease Control and China Meteorological Administration. The correlation between malaria incidence and meteorological factors was analyzed using Pearson correlation analysis. The generalized additive model (GAM) was applied to investigate the relationship between monthly local malaria cases and meteorological factors. Results showed that there was a weak positive correlation between minimum temperature, mean relative humidity as well as minimum relative humidity and local malaria incidences. While a complex nonlinear relationship between the vectorial capacity, relative humidity and the incidence of malaria was detected. Malaria transmission increases when the vectorial capacity was greater than 10 (VCAP>10) or the average relative humidity was between 55% and 70%. The malaria transmission declines when relative humidity above 70%. The relationship between meteorological factors and the incidence of local malaria is well explained by GAM, and there is a complex nonlinear relationship between vectorial capacity, relative humidity and malaria incidence.

malaria; generalized additive model; meteorological factor; vectorial capacity

10.3969/j.issn.1002-2694.2017.08.002

国际发展研究中心(IDCR)(No.105509-00001002-024&108100-001)，国家自然科学基金(No.81573261)，江苏省科技厅项目(No.BM2015024)和国家科技计划(No.2012ZX10004-220)联合资助。

杨国静，Email：guojingyang@hotmail.com

1.江苏省血吸虫病防治研究所，无锡 214064； 2.江南大学公共卫生研究中心，无锡 214122； 3.杭州电子科技大学，杭州 310018； 4.瑞士热带病研究所流行病学与公共卫生学院，巴塞尔 40； 5.巴塞尔大学，巴塞尔 40

Supported by the International Development Research Center (No.105509-00001002-024&108100-001), the National Natural Science of China (No.81573261),the Jiangsu Provinicial Department of Science and Technology Project (No.BM2015024), and the National Science and Technology Major project (No.2012ZX10004-220)

R382.3

：A

：1002-2694(2017)08-0674-06

2017-02-13编辑：梁小洁