基于新型降阶模型的网格加筋圆柱壳频率分析
2017-09-03李玉韦程耿东
李玉韦,王 博,程耿东
(大连理工大学工业装备结构分析国家重点实验室工程力学系,大连 116024)
基于新型降阶模型的网格加筋圆柱壳频率分析
李玉韦,王 博,程耿东
(大连理工大学工业装备结构分析国家重点实验室工程力学系,大连 116024)
针对网格加筋圆柱壳频率分析计算量大的问题,提出一种基于多项式及梁单元形函数的模型降阶方法,即运用多项式及梁单元形函数将复杂结构有限元的节点位移转化为主节点位移,实现模型降阶。并通过控制多项式阶数及梁单元个数来调整降阶模型的分析精度,而降阶模型的计算效率较精细模型有显著提高。以网格加筋圆柱壳为例,对比本文提出的模型降阶方法与3-D实体模型及其他模型降阶方法的频率分析结果,结果表明,提出的模型降阶方法不仅能捕捉到结构的整体模态,还能反映出结构部分局部模态,适用范围广,能够为工程结构设计提供简单有效的计算模型。
多项式函数;梁单元形函数;模型降阶;网格加筋圆柱壳;频率分析
0 引言
网格加筋圆柱壳由于较高的比刚度和比强度广泛应用于航空航天结构,如运载火箭的燃料贮箱和级间段等[1-2]。运载火箭结构的弯曲、扭转、纵向等整体模态及部分局部模态是载荷计算、姿态稳定性分析、速率陀螺仪安放位置确定等工作的基础。详细描述结构细节的有限元模型往往具有几十万甚至上千万个自由度,几乎不可能采用这样的模型进行结构动力特性分析,而且基于此类有限元模型得到的频率分析结果中含有大量的局部模态,反而干扰了对结构总体性能的认识。因此,在结构设计初期,选取合适的计算模型是开展相关分析的前提。
为提高网格加筋圆柱壳频率分析的计算效率,邢誉峰等[3]、潘忠文等[4]研究了加筋圆柱壳弯曲刚度的面积等效方法和惯性矩等效方法,分别分析了面积等效时截面惯性矩的精度和惯性矩等效时面积的等效精度,提出了用于加筋圆柱壳频率分析的等效厚度模型,并指出等效厚度模型可直接用于计算结构的弯曲和纵向频率,但扭转频率计算精度较差,需进行修正。Cheng等[5]、Cai等[6-7]通过改进渐近均匀化方法(NIAH)预测三维周期性结构刚度特性,将复杂结构等效为具有类似刚度特性的简单结构。这种方法不需要复杂的数学推导,可以利用商业软件中提供的各种单元和建模技术,使单胞模型保持较小的规模。郑淑飞等[8-9]提出一种基于变形修正的动力模型简化方法,该方法以加筋圆柱壳精细有限元模型为基础,根据运动同步性假设将结构分成若干同步性区域,建立结构整体位移与局部位移模式之间的转换关系,实现模型降阶,但位移转换阵中未考虑原结构的转角自由度,对含有梁、壳等元组件结构的分析精度较差。在此基础上,王文胜等[10,12]、Cheng等[11]将复杂结构模型划分为不同的梁段,通过梁平截面假设及位移插值函数将每一梁段降阶为一个梁超单元,按照一定的次序组装成超梁模型,并引入横向剪切系数修正梁超单元的刚度阵。针对具有大开口的结构,本文通过数值方法引入了表示截面翘曲变形的翘曲基向量,进一步提高了扭转频率的计算精度,本文称该方法为平截面梁模型方法。文献[12]通过网格加筋结构、含开口光筒结构验证了平截面梁模型方法的有效性,但该方法仅适用于计算结构的整体频率,无法获得结构的局部模态。
本文在基于多项式函数的动力模型降阶方法的基础上,提出一种基于多项式及梁单元形函数混合的模型降阶方法,该方法将结构沿轴向划分若干个梁单元,利用多项式及梁单元形函数建立所有节点位移与梁单元节点位移之间的转换关系,实现结构降阶。建立的降阶模型不仅可用于计算结构的整体频率,还可通过增加多项式项数及梁单元个数获得结构的部分局部模态。文中首先以网格加筋圆柱壳为例,对比本文提出的模型降阶方法与3-D实体模型及其他模型降阶方法的频率分析结果。然后,针对含开口网格加筋圆柱壳结构,文中通过数值方法引入翘曲变形改善降阶模型扭转频率的计算精度。数值结果表明,本文提出的模型降阶方法计算精度较高。
1 模型降阶方法
模型降阶是利用原结构有限元模型的数学或力学特征,选择一组合适的减缩基向量,将复杂结构动力学问题降阶。不考虑阻尼影响,原结构动力分析的有限元控制方程可表示为:
(1)

引入位移转换矩阵T(r×k)(r≪k),复杂结构的位移可表示为:
U=TQ
(2)
其中,Q(k×1)是降阶模型的位移。将式(2)带入式(1),并左乘TT,得到降阶模型的动力学方程:
(3)
其中,MR=TTMT,KR=TTKT是降阶模型的质量阵和刚度阵,FR=TTF是降阶模型的载荷向量。通过求解特征方程(4)获得降阶模型的固有频率。
(KR-λkkMR)φkk=0
(4)
其中,λkk为结构第kk阶频率,φkk为与其对应的特征向量。
不同模型降阶方法的主要区别在于减缩基向量T的构造,不同的减缩基构造方法可能导致不同的计算精度及计算效率,文献[13-16]给出了不同的模型降阶方法,此处不再赘述。
2 基于多项式及梁单元形函数的模型降阶方法
考虑如图1所示的复杂结构,OXYZ为全局坐标系,将结构沿轴向划分为若干个梁单元,取每个梁单元的节点为主节点。首先利用多项式建立任意一点与其梁轴线上的投影点之间的位移转换关系,再通过梁单元形函数建立投影点与主节点之间的位移转换关系,通过两次位移转换可以建立梁单元内任意节点位移与其主节点位移之间的转换关系,进而得到用于模型降阶的减缩基向量。具体步骤如下:
结构上任意一点与其投影点之间的位移转换关系如式(5)所示:
uj=Rjqi
(5)
展开形式为:
(6)

ujx=qix1+yqix2+zqix3+y2qix4+yzqix5+z2qix6=Fτjqixτ
ujy=qiy1+yqiy2+zqiy3+y2qiy4+yzqiy5+z2qiy6=Fτjqiyτ
ujz=qiz1+yqiz2+zqiz3+y2qiz4+yzqiz5+z2qiz6=Fτjqizτ
(7)
位移转换矩阵Rj为:
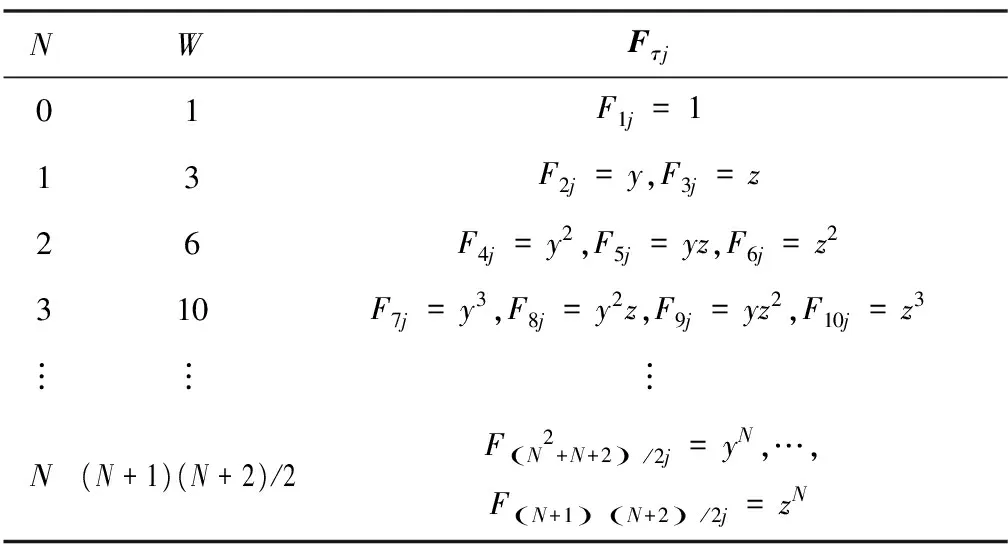
(8)
投影点位移与其所在梁单元主节点位移的转换关系为:
(9)

表2 梁单元形函数
由式(5)及式(9),可知结构上任意一点与其所在梁单元主节点之间的位移转换阵为:
(10)
梁单元i内所有节点的位移与主节点的位移转换关系为:
例如:在学习乙酸乙酯的制备时,通过动画模拟的技术可以清晰直观的把乙酸和乙醇反应时的断键、成键部位展示出来,学生会对这类多原子的化合物的反应机理产生更深入的了解,提高了化学实验教学的教学效率
(11)
(12)
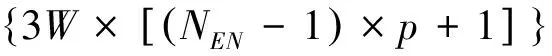
3 数值算例
通过两个具体算例的频率分析,比较本文提出的模型降阶方法与其他模型降阶方法的分析结果,证明本方法的有效性。
3.1 网格加筋圆柱壳算例
算例1为图2所示的正置正交网格加筋圆柱
壳,其中,横向筋条11根,轴向筋条4根。筒壳长10020mm,外半径为1000mm,蒙皮厚10mm,筋条高度为50mm,筋条厚20mm。采用铝合金材料,弹性模量为73GPa,泊松比为0.3,密度为2.7×10-3g/mm3。采用3-D实体单元(solid45)建立有限元模型,并沿筋条高度及厚度方向局部加密,整体网格密度为100mm,共有17360个节点,52080个自由度。
为对比不同梁单元个数对降阶模型计算精度的影响,本文利用B4梁单元建立投影点位移与其所在梁单元主节点之间的位移转换关系,采用3阶多项式(N=3)建立截面任意一点位移与投影点位移的转化关系。表3给出了固支-自由边界条件下的不同梁单元个数(Nm)对网格加筋圆柱壳结构整体频率的影响。

表3 固支-自由状态下不同梁单元个数对整体频率的影响
同样以图2所示网格加筋柱壳为例,表4讨论了多项式阶数(N)对降阶模型频率计算精度的影响,假定降阶模型沿轴向方向划分20个B4梁单元。为说明本文提出方法的有效性,采用模态置信因子对降阶模型和原结构的模态作比较。模态置信因子MAC[17]定义为:
(13)
其中,φA代表原模型计算得到的模态,φR代表降阶模型的模态。一般情况下,当MAC值大于0.7时,认为二者相似性较好;当MAC值小于0.5时,相似性较差。
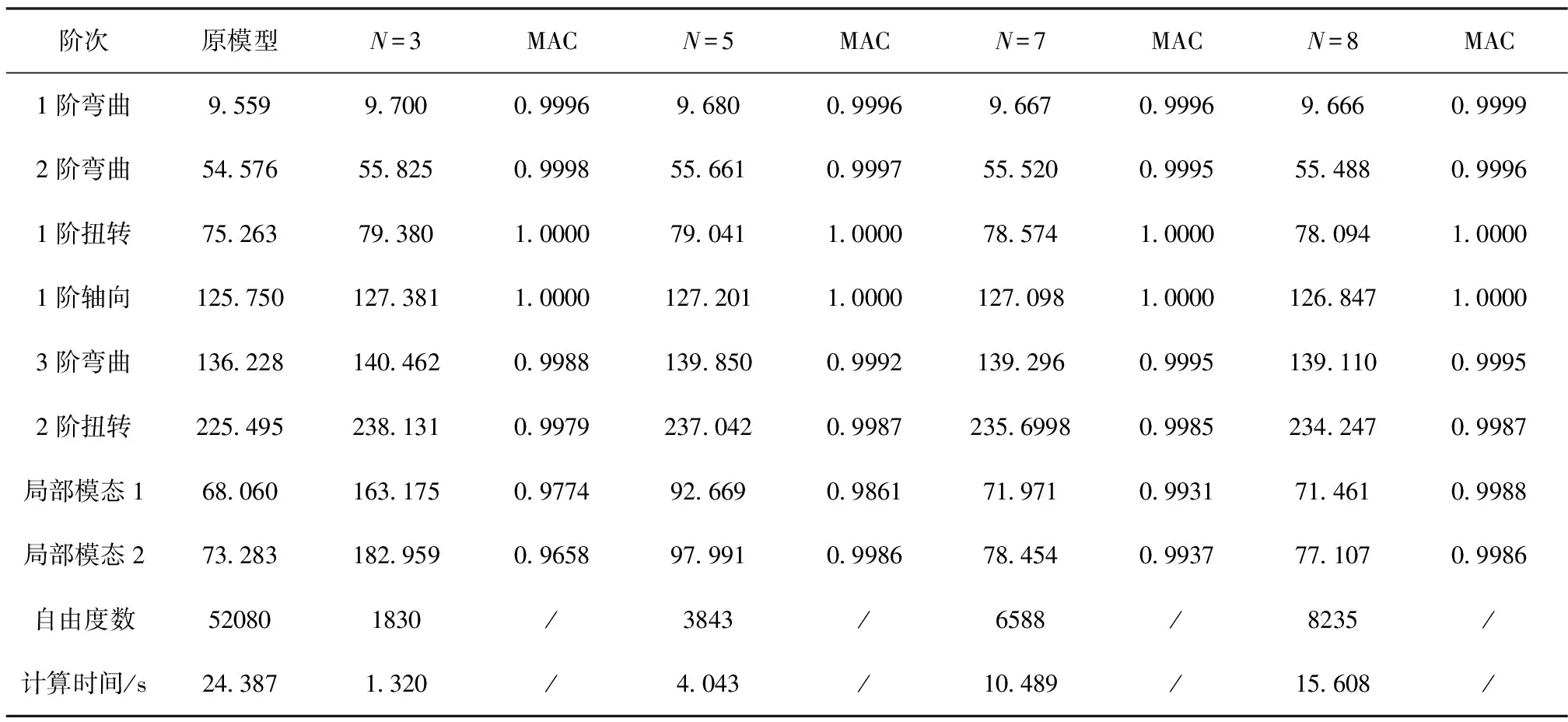
表4 固支-自由状态下多项式阶数对降阶模型频率的影响(单位:Hz)
由表4可知,降阶模型的计算精度能满足工程设计的需要,得到的整体模态与原模型的模态具有极高的相似性,降阶模型合理地保留了原模型的特征,计算效率有很大提高。此外,本文提出的模型降阶方法不仅能捕捉到原模型的整体模态,还能获得原结构某些局部模态,如当多项式阶数N=7时,降阶模型得到的局部频率计算误差为7.05%,计算时间为原精细模型的43%。进一步提高多项式阶数至N=8时,局部频率的计算误差为5.21%,计算时间为精细模型的63%。图3~图6给出部分模态对比图。因此,本文提出的模型降阶方法进一步拓宽了降阶模型的适用范围,为设计人员提供了一个简单有效的计算模型。
3.2 含开口网格加筋圆柱壳算例
为满足适用性和维修性要求,在运载火箭结构上要设计各种开口,含开口网格加筋圆柱壳发生扭转变形时,截面上各点沿轴线方向有不同的位移,产生了翘曲变形,Vlasov[18]提出了薄壁杆件约束扭转时截面变形规律,认为横截面上各点的翘曲轴向变形沿杆件横截面按各点的扇形坐标分布,而对于复杂结构,计算扇形坐标是非常困难的。本文通过数值方法[12]实现截面变形的精确描述,该方法通过对模型施加单位扭矩,利用静力分析计算得到各个截面上的节点位移,进而通过Schmidt正交化引入翘曲基向量。具体步骤如下:
梁单元内所有节点的变形可表示为:
(14)
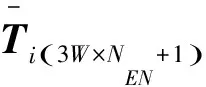
(15)
梁单元内各主节点的位移分量可表示为:
(16)
(17)
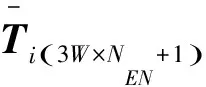
(18)
将式(18)代入式(12)得到考虑翘曲变形的位移转换阵T。
算例2为图7所示的含开口网格加筋圆柱壳,结构尺寸及筋条分布情况和算例1相同,矩形开口位于轴向1/2位置处,开口长度L=1980mm,宽度H=692.8mm,采用铝合金材料,弹性模量为73GPa,泊松比为0.3,密度为2.7×10-3g/mm3。有限元模型共有节点16912个,自由度为50736个。
表5给出了引入翘曲基向量前后的降阶模型频率计算结果与ANSYS计算结果的对比,其中第1、2、4、5阶为弯曲模态,第3阶为扭转模态,降阶模型轴向仍采用20个B4梁单元。
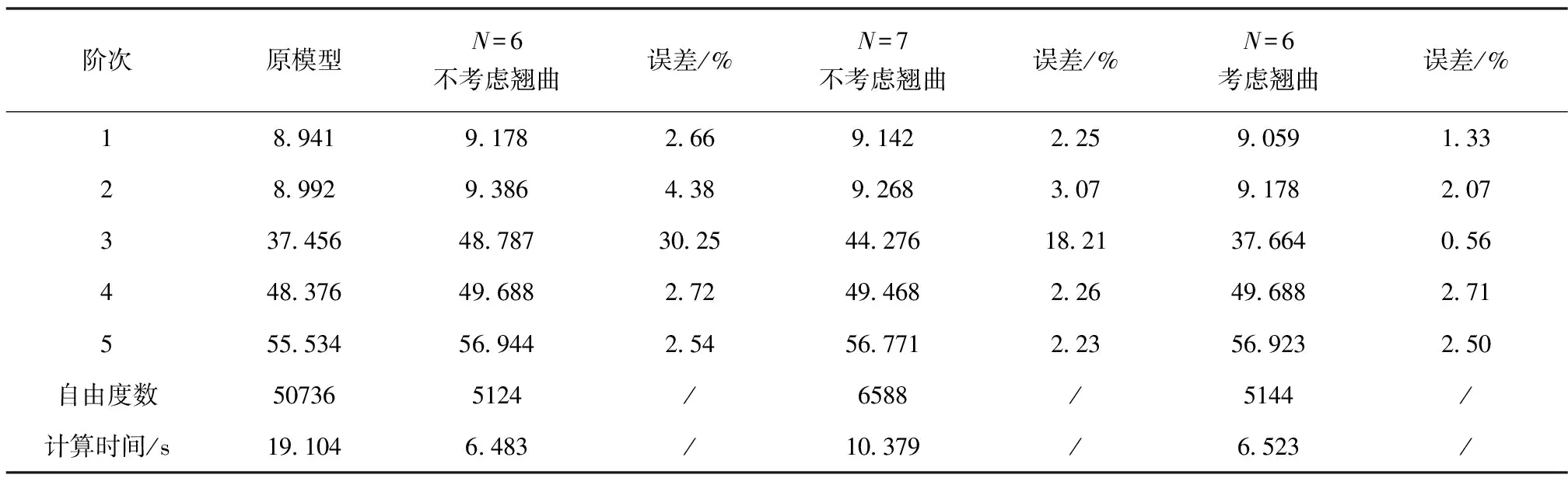
表5 固支-自由状态下含开口网格加筋圆柱壳降阶模型频率计算结果(单位:Hz)
由表5可看出,仅通过增加多项式阶数可提高降阶模型的计算精度,当N=7时,弯曲频率的计算误差最高为3.07%,但扭转频率的计算误差仍高达18.21%,这是由于降阶模型不能精确描述截面的扭转变形,导致扭转刚度增大。引入截面翘曲基向量后,扭转频率的计算误差降为0.56%,降阶模型的计算精度大幅提高,计算时间为精细模型的34.1%。图8给出了考虑翘曲变形前后降阶模型得到的扭转模态,对比图中红色区域的变形可看出,引入翘曲基向量的降阶模型能更好地描述具有大开口结构的实际变形。
4 结论
本文针对网格加筋圆柱壳结构提出一种新的模型降阶方法,该方法将复杂结构划分为若干个梁单元,将每个梁单元的节点作为主节点,利用多项式函数建立结构任意节点与其所在轴线上投影点之间的位移转换关系,再利用梁单元形函数建立投影点与主节点之间的位移转换关系,进而实现模型降阶。针对含开口网格加筋结构,文中通过数值方法引入翘曲变形,提高降阶模型扭转频率的计算精度。
本文提出的模型降阶方法不需要大量的矩阵运算,计算效率高,可利用商业软件作为一个黑箱来实现,并通过调整多项式阶数及梁单元的个数控制降阶模型的计算精度。文中首先以网格加筋柱壳为例验证该降阶方法的有效性,计算结果表明该降阶模型合理地保留了原结构的特征,不仅能用于计算结构的整体频率,还可捕捉到结构的某些局部模态。其次,文中将该方法应用于含开口网格加筋柱壳的频率分析中,通过数值方法引入翘曲变形提高降阶模型扭转频率的计算精度。因此,本文提出的模型降阶方法扩展了降阶模型的应用范围,为设计人员提供了一个简单有效的计算模型。
本文提出的模型降阶方法可以很方便建立不同约束条件下降阶模型,在此基础上,研究多工况、多边界条件下结构的动力特性分析及动力优化设计是下一步开展的工作。
[1] Hao P, Wang B, Tian K, et al. Efficient optimization of cylindrical stiffened shells with reinforced cutouts by curvilinear stiffeners[J]. AIAA Journal, 2016, 54 (4):1-14.
[2] Wang B, Tian K, Hao P, et al. Numerical-based smeared stiffener method for global buckling analysis of grid-stiffened composite cylindrical shells[J]. Composite Structures, 2016, 15(2): 807-815.
[3] 邢誉峰, 潘忠文,杨阳.蒙皮加筋圆柱壳弯曲频率的三种计算模型[J].北京航空航天大学学报, 2012, 38 (4):438-443.
[4] 潘忠文,王小军,马兴瑞,等. 基于梁模型的蒙皮加筋结构纵横扭一体化建模研究[J].中国科学: 技术科学, 2014, 44 (5) :517-524.
[5] Cheng G D ,Cai Y W, Xu L. Novel implementation of homogenization method to predict effective properties of periodic materials[J]. Acta Mechanica Sinica, 2013, 29 (4):550-556.
[6] Cai Y W, Xu L, Cheng G D. Novel numerical implementation of asymptotic homogenization method for periodic plate structures[J]. International Journal of Solids and Structures, 2014, 51 (1) :284-292.
[7] 蔡园武. 周期性板结构的渐近均匀化方法及微结构优化 [D]. 大连:大连理工大学. 2014.
[8] Zheng S F, Ding H. A model reduction method for dynamic analysis based on deformation modification and local rigid body mode[J]. Mechanics in Engineering, 2008, 30 (9):31-35.
[9] 郑淑飞,丁桦. 基于变形修正的局部刚体化动力模型简化方法[J].力学与实践, 2008, 30 (6) :31-34.
[10] 王文胜,程耿东,郝鹏. 基于超梁降阶模型的蒙皮加筋圆柱壳频率分析[J].固体火箭技术, 2015, 38 (3) :401-406.
[11] Cheng G D, Wang W S. Fast dynamic analysis of complicated beam-type structure based on reduced super beam model[J]. AIAA Journal, 2014, 52 (5) :952-963.
[12] Wang W S, Cheng G D, Li Q H. Fast dynamic performance optimization of complicated beam-type structures based on two new reduced physical models[J]. Engineering Optimization, 2013, 45 (7):835-850.
[13] Guyan R J. Reduction of stiffness and mass matrices[J]. AIAA Journal, 1965, 3 (2) :380.
[14] Irons B. Structural eigenvalue problems-elimination of unwanted variables[J]. AIAA Journal, 1965, 3 (5):961-962.
[15] Carrera E, Miglioretti F, Petrolo M. Computations and evaluations of higher-order theories for free vibration analysis of beams[J]. Journal of Sound and Vibration, 2012, 331 (19) :4269-4284.
[16] Carrera E, Zappino E, Filippi M. Free vibration analysis of thin-walled cylinders reinforced with longitudinal and transversal stiffeners[J]. Journal of Vibration and Acoustics, 2013, 135(1):011019.
[17] Allemang R J, Brown, D L. A correlation coefficient for modal vector analysis[M]. Proceedings of the Proceeding of the 1st international modal analysis conference, Orlando, FL. Union College, Schenectady, NY, 1982:110-116.
[18] Vlasov V Z. Thin-Walled elastic beams(2nd edn)[M].Moscow, 1959:57-162.
Frequency Analysis of Stiffened Cylinder Based on NovelReduced Order Model
LI Yu-wei, WANG Bo, CHENG Geng-dong
(State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics,Dalian University of Technology, Dalian 116024, China)
A novel reduced order model is proposed to determine the natural frequencies of the stiffened cylinder in this study, which is established by using a reduction basis along with the polynomial interpolation function and shape function of beams. The basic idea is to convert the displacements of FEM nodes to the master nodes with a few generalized DOFs. The proposed ROM can gain a significant reduction of computational cost without sacrifice of accuracy. Typical stiffened cylinder are studied and the outcomes are validated by benchmark studies. The results show that the reduced order model has the ability to identify shell lobe-type modes, which can be served as an efficient alternative model during initial design.
Polynomial interpolation function; Shape function of beams; Model reduction; Stiffened cylinder; Frequency analysis
2017-03-27;
2017-04-27基金项目:国家“973”计划(2014CB049000);国家自然科学基金(11372062, 11402049)
李玉韦(1989-),男,在读博士,主要研究方向:结构动力模型降阶及优化。E-mail:liyuwei@mail.dlut.edu.cn通讯作者:王博(1978-),男,教授,主要从事结构多学科优化、航天先进材料与结构设计和轻质结构抗冲击分析与设计。E-mail:wangbo@dlut.edu.cn
V415
A
2096-4080(2017)01-0041-08
